【蓝桥杯每日一题】差分算法
🍎 博客主页:🌙@披星戴月的贾维斯
🍎 欢迎关注:👍点赞🍃收藏🔥留言
🍇系列专栏:🌙 蓝桥杯
🌙我与杀戮之中绽放,亦如黎明的花朵🌙
🍉一起加油,去追寻、去成为更好的自己!
蓝桥杯倒计时 44天
文章目录
- 🍎、差分
- 🍎、例题分析
- 🍇、(AcWing)差分
- 🍇、(AcWing)差分矩阵
- 🍇、(AcWing)改变数组元素
- 🍎、总结
提示:以下是本篇文章正文内容,下面案例可供参考
🍎、差分
🍉、差分的简单概念
差分在数学领域的理解:有数列a1 a2 a3……an……,其中an+1= an + d( n = 1,2,…n )d为常数,称为公差, 即 d = an+1 -an , 这就是一个差分, 通常用D(an) = an+1- an来表示,于是有D(an)= d , 这是一个最简单形式的差分方程。
差分在计算机领域的理解:差分是前缀和的逆运算,差分的作用是在O(1)的时间复杂度下,让一段区间,例如是[i, n]区间内的每一个数都加或者减同一个数。
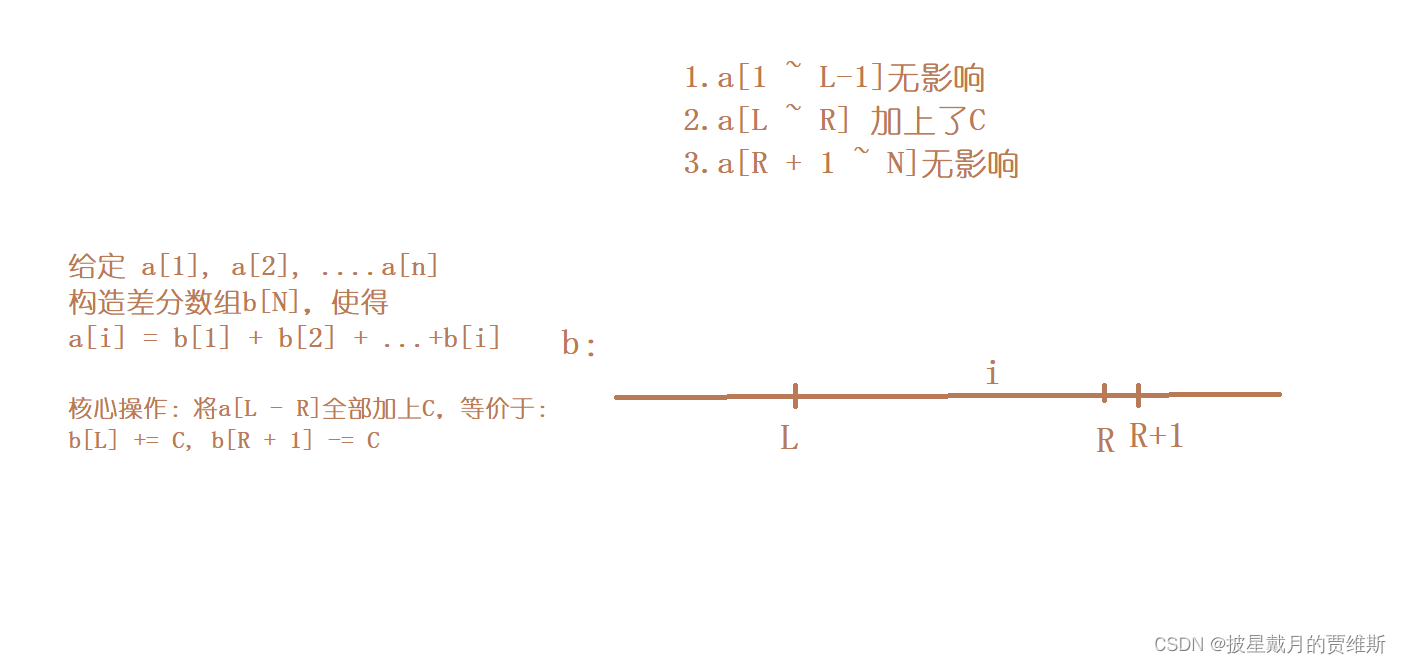
一维差分的公式:s[L] += c , s[R + 1] -= c;
其中L是区间的左端点,R是区间的右端点。
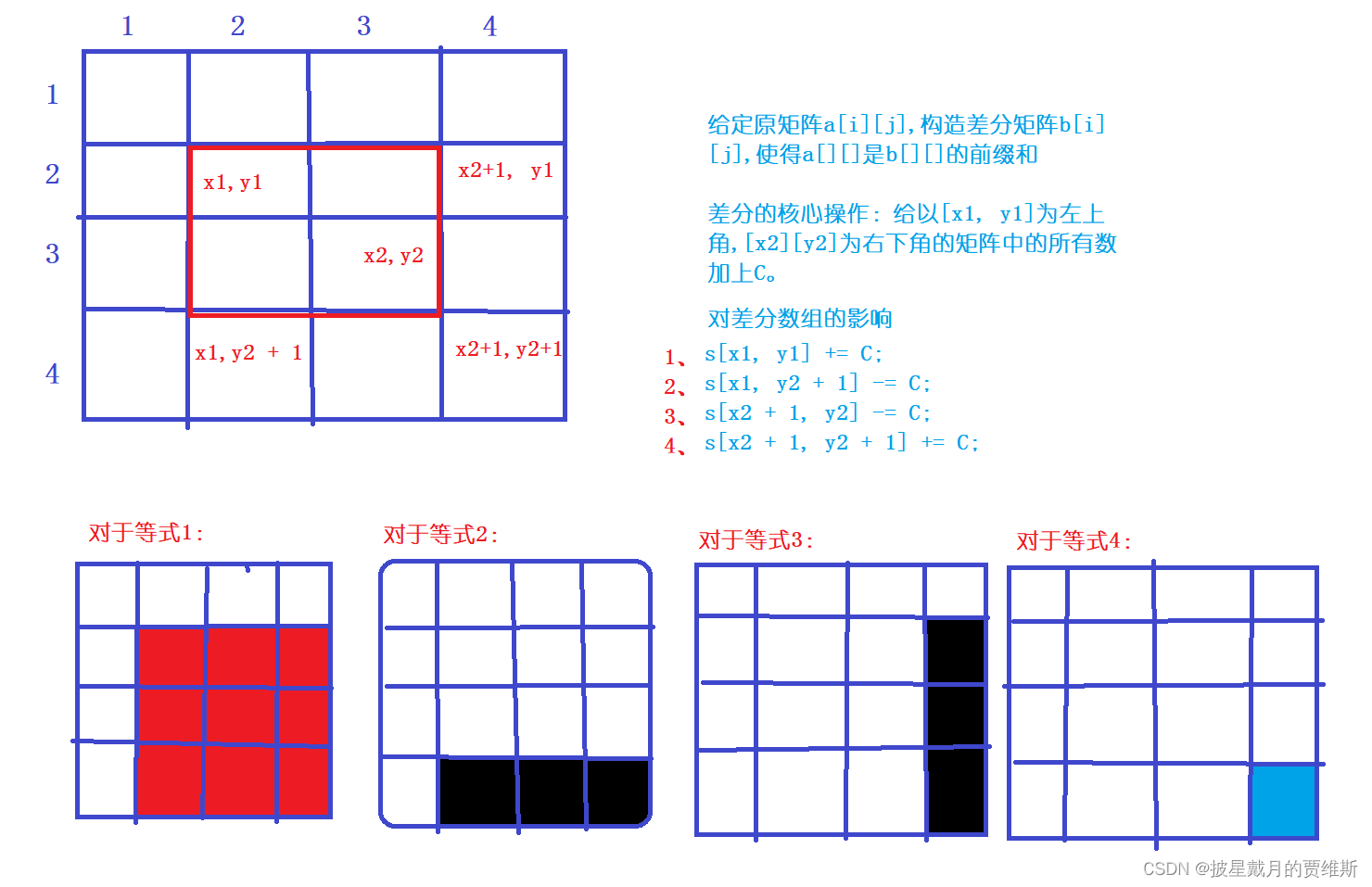
二维差分的公式:S[x1][y2] += c; s[x1][y2 + 1] -= c;
S[x2 + 1] -= c; s[x2 + 1][y2 + 1] += c;
对于差分数组的理解:原数组a[]是差分数组b[]的前缀和,a[i] = b[0] + b[1] + b[2] + … + b[i],所以在最后输出结果时一维差分公式:a[i] = a[i - 1] + b[i];
二维差分最后输出结果的公式是: a[i][j] = a[i - 1][j] + a[i][j - 1] + b[i][j]
🍉、图解一维前缀和
🍉、图解二维前缀和
🍎、例题分析
🍇、(AcWing)差分
本题链接: 差分

简单分析题意:就是在q次询问中,每次在原数组的一段区间上加上一个值C,最后输出q次询问后的结果。
代码示例:
#include<iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], b[N];
void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c;
}
int main ()
{cin >> n >> m;for(int i = 1; i <= n; i++){cin >> a[i];insert(i, i, a[i]);//对b[i]的初始化}while(m --){int l, r, c;cin >> l >> r >> c;insert(l, r, c);}for(int i = 1; i <= n; i++){a[i] = a[i - 1] + b[i];cout << a[i] << ' ';}cout << endl;return 0;
}
🍇、(AcWing)差分矩阵
本题链接: 差分矩阵

简单分析题意:就是在q次查询中,每次在一个区间内加/减一个值。
代码示例:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int b[N][N], a[N][N];
int n, m, q;
void add(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x1][y2 + 1] -= c;b[x2 + 1][y1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main ()
{cin >> n >> m >> q;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++){scanf("%d", &a[i][j]);add(i, j, i, j, a[i][j]); // 每次输入一个a[i],就要初始化一下b差分数组}while(q --){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;add(x1, y1, x2, y2, c);}for(int i = 1; i <=n; i++){for(int j = 1; j <= m; j++){a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];//这里使用二维前缀和公式printf("%d ", a[i][j]);}puts("");}return 0;
}
🍇、(AcWing)改变数组元素
本题链接: 改变数组元素

分析题意:
代码示例:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;const int N = 200010;
int b[N];
int n;
int main ()
{int t;cin >> t;while(t --){scanf("%d", &n);memset(b, 0, 4 * (n + 1));for(int i = 1; i <= n; i++){int x;scanf("%d", &x);x = min(x, i);int l = i - x + 1, r = i;//差分数组的左右两端b[l]++, b[r + 1]--; //差分操作的模板} //求原数组,就是差分数组的前缀和for(int i = 1; i <= n; i++){b[i] += b[i - 1]; //差分和前缀和是互逆操作}for(int i = 1; i <= n; i++)printf("%d ", !!b[i]); // 原来是0的还是0,原来大于等于1的就变为1了。puts("");}return 0;
}
🍎、总结
本文简要介绍了差分的简要概念和几道差分的经典例题,希望大家读后能有所收获!
相关文章:

【蓝桥杯每日一题】差分算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...

MyBatis Plus 数据库字段加密处理
目录1.场景介绍2.Maven依赖2.AESUtil.java 加解密工具类3.字段处理类4.修改 MyBatis Plus 查询4.1 修改表对应实体类4.2 修改加密字段对应属性4.3 修改 xml 使用 ResultMap4.4 修改 xml 中 el 表达式5.测试结果6.MyBatis Plus 缺陷补充:测试实例1 查询测试1.1 查询信…...

openpose在win下环境配置
1.下载OpenPose库 以下二选一进行下载源码 (1)git进行下载 打开GitHub Desktop或者Powershell git clone https://github.com/CMU-Perceptual-Computing-Lab/openpose cd openpose/ git submodule update --init --recursive --remote(2)在github上手动下载 由于下载环境问…...

【剑指offer-C++】JZ16:数值的整数次方
【剑指offer】JZ16:数值的整数次方题目描述解题思路题目描述 描述:实现函数 double Power(double base, int exponent),求base的exponent次方。 注意: 1.保证base和exponent不同时为0。 2.不得使用库函数,同时不需要…...

了解Axios及其运用方式
Axios简介 axios框架全称(ajax – I/O – system): 基于promise用于浏览器和node.js的http客户端,因此可以使用Promise API 一、axios是干啥的 说到axios我们就不得不说下Ajax。在旧浏览器页面在向服务器请求数据时,…...
【LeetCode】剑指 Offer(7)
目录 写在前面: 题目剑指 Offer 17. 打印从1到最大的n位数 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 18. 删除链表的节…...

Python:try except 异常处理整理
目录 一、try except异常处理的语句格式 二、获取相关异常信息 (1)sys.exec_info() 三、traceback模块的常用方式 (1)traceback.print_tb(tb, limitNone, fileNone) 打印指定堆栈异常信息 (2)tracebac…...

Redis Lua脚本的详细介绍以及使用入门
Redis Lua脚本的详细介绍以及使用入门。 文章目录Redis Lua脚本的引入开源软件的可扩展性Redis的扩展性脚本Redis Lua脚本的基本使用通过EVAL命令执行Lua脚本通过脚本与Redis交互Java中调用Redis Lua脚本Java调用Lua脚本的方式Redis Lua脚本的使用建议脚本缓存脚本缓存稳定性脚…...

synchronized和ReentrantLock有什么区别呢?
第15讲 | synchronized和ReentrantLock有什么区别呢? 从今天开始,我们将进入 Java 并发学习阶段。软件并发已经成为现代软件开发的基础能力,而 Java 精心设计的高效并发机制,正是构建大规模应用的基础之一,所以考察并发…...
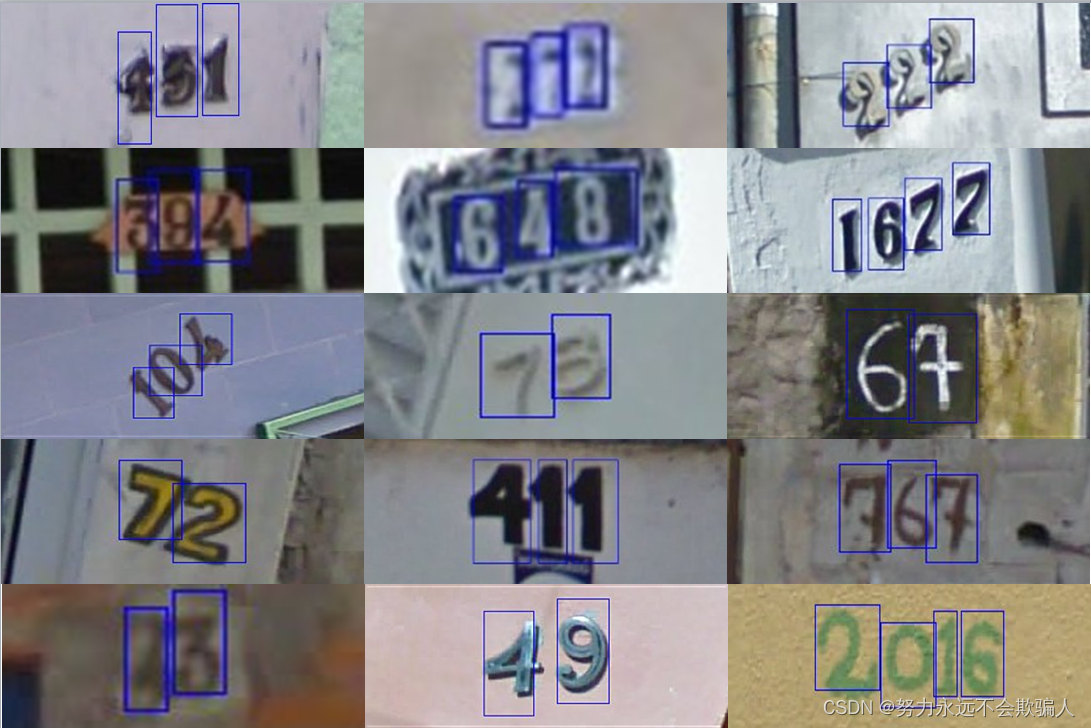
SVHN数据集下载及使用方法
街景门牌号数据集(SVHN),这是一个现实世界数据集,用于开发目标检测算法。它需要最少的数据预处理过程。它与 MNIST 数据集有些类似,但是有着更多的标注数据(超过 600,000 张图像)。这些数据是从…...

产业安全公开课:2023年DDoS攻击趋势研判与企业防护新思路
2023年,全球数字化正在加速发展,网络安全是数字化发展的重要保障。与此同时,网络威胁日益加剧。其中,DDoS攻击作为网络安全的主要威胁之一,呈现出连年增长的态势,给企业业务稳定带来巨大挑战。2月21日&…...

Docker 容器命令 和安装各种镜像环境
CentOS安装Docker 1.1.卸载(可选) 如果之前安装过旧版本的Docker,可以使用下面命令卸载: yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotat…...
【数据结构】顺序表的深度剖析
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 🚀数据结构专栏ÿ…...

当面试官问“你的SQL能力怎么样”时,怎么回答才不会掉进应聘陷阱?
在某平台看到一个比较实际的问题,在这里分享给职场新人。 SQL已经是职场最常用的一种编程语言,所以应聘技术或非技术岗位,都可能会被问道一个问题:你的SQL能力怎么样? 对于职场新人来说(SQL高手可以无视下…...

AI作画—中国画之山水画
山水画,简称“山水”,中国画的一种,描写山川自然景色为主体的绘画。山水画在我国绘画史中占有重要的地位。 山水画形成于魏晋南北朝时期,但尚未从人物画中完全分离。隋唐时始终独立,五代、北宋时趋于成熟,…...

Java:Java与Python — 编码大战
Java和Python是目前市场上最热门的两种编程语言,因为它们具有通用性、高效性和自动化能力。两种语言都有各自的优点和缺点,但主要区别在于Java 是静态类型的,Python是动态类型的。它们有相似之处,因为它们都采用了“一切都是对象”…...

山东专精特新各地市扶持政策
青岛市奖励政策:新认定为市隐形、省“专精特新”及省瞪羚、角兽的我市企业,分别给予50万元、30万元、50万元、300万元的一次性奖励。奖励金额:省级30万济南市奖励政策:对被认定的国家专精特新 “小巨人”企业一次性给予200万元奖励…...
持续事务管理过程中的事件驱动
比较官方的定义:事件驱动是指在持续事务管理过程中,进行决策的一种策略,即跟随当前时间点上出现的事件,调动可用资源,执行相关任务,使不断出现的问题得以解决,防止事务堆积。在计算机编程、公共…...

【手把手一起学习】(三) Altium Designer 20 原理图库添加元件
1 添加元件 元件符号是元件在原理图上的表现形式,主要由边框、管脚、名称等组成,原理图库中的元件管脚(顺序,间距等)与电子元件实物的引脚严格对应,绘制原理图库时,一定参考元件规格书和芯片数据手册中的说明…...

设计模式-行为型模式:观察者模式
目录 1、简介 2、组成部分 3、优缺点 4、使用场景 5、代码实现 1、简介 观察者模式是一种软件设计模式,它定义了一种一对多的依赖关系,让多个观察者对象同时监听一个主题对象,当主题对象发生变化时,所有的观察者对象都会得到…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
