【数据结构】七大排序
文章目录
- 💐1. 插入排序
- 🌼1.1 直接插入排序
- 🌼1.2 希尔排序
- 💐2. 选择排序
- 🌼2.1 直接选择排序
- 🌼2.2 堆排序
- 💐3. 交换排序
- 🌼3.1 冒泡排序
- 🌼3.2 快速排序
- 🌼3.2.1 快速排序优化
- 🌼3.2.2 快速排序非递归
- 💐4. 归并排序
- 🌼4.1 基本思想
- 💐6. 海量数据进行排序
**内部排序:**数据全部放在内存中的排序
**外部排序:**如果数据量比较大,内存中放不下,不能在内外存之间进行数据的移动,需要放在硬盘上进行排序,这样的排序称为外部排序;
学习排序要熟练的掌握每一种排序的时间复杂度,稳定性,这样在场景中才可以运用自如;
💐1. 插入排序
🌼1.1 直接插入排序
遍历集合中的每一个元素,每一个元素都作为一个关键码与前面的元素作比较,如果小于前面的元素,前面的元素就向后移动,直到遇见比关键码大的元素,就插入在该元素后一个位置,这也会使得每一个数值作为关键码时,前面的元素都是已经排好序的;


直接插入排序特性:
-
元素集合越接近有序,直接插入排序时间效率就越高(因为,如果前面都是13456已经排序好的,忽然遇见一个2,那么前面需要移动的元素就会更多)
-
时间复杂度:
最好的情况是O(n),数组本来就是有序的 例如 1 2 3 4 5
最坏情况是O(n^2),数组是逆序的 例如 5 4 3 2 1
-
空间复杂度:O(1)
-
稳定性:稳定
这里提到了稳定性,下面来解释一下什么是稳定性:
稳定性:假设在一个序列中,出现了相同的数据,经过排序之后,这些相同的数据之间的相对位置保持不变,比如,r[i] = r[j], 在排序之前,r[i] 在 r[j] 之前,排序之后,r[i] 仍然在 r[j] 之前,则这样的排序称为是稳定的,反之是不稳定的;而且一个稳定的排序是可以变成不稳定的,但是一个不稳定的排序是不可以变成稳定的;

代码实现
//直接插入排序public void insert(int[] array) {//元素数量不能小于1if(array.length < 1) {return;}//定义i遍历每一个元素for(int i = 1; i<array.length; i++) {//定义j遍历i前面的元素int j = i-1;//定义关键码key保存i对应的值int key = array[i];for(; j>=0; j--) {//符合条件进行移动if(array[j] > key) {//如果这里变成>=就变成了不稳定的array[j+1] = array[j];}else {break;}}//最后将key插入array[j+1] = key;}}
🌼1.2 希尔排序
思想:希尔排序又称缩小增量法, 定义一个增量值,将集合中的数据按照这个增量值进行分组,每一组中元素之间的距离都是这个增量值,每一次缩小增量时都进行了预排序,最后增量值为1时,完成排序;



希尔排序特性:
-
希尔排序是对直接插入排序的优化
-
当gap > 1 时都是预排序,目的是为了让数组跟趋近有序,当gap == 1时,数组已经接近有序了,这样整体而言就可以达到优化效果;
-
希尔排序的时间复杂多每办法确定,因为gap的取值方法很多,导致很难去计算,一般都会对gap进行除2来缩小增量
-
稳定性:不稳定
代码实现:
//希尔排序public void shellSort(int[] array) {//定义增量int gap = array.length / 2;while(gap > 0) {for(int i = gap; i<array.length; i++) {int j = i - gap;int key = array[i];for(; j>=0; j -= gap) {if(array[j] > key) {array[j+gap] = array[j];}else{break;}}array[j+gap] = key;}gap /= 2;}}
💐2. 选择排序
🌼2.1 直接选择排序
思想:每一次从待排序的数据集合中取出最小的一个,然后与序列起始位置处的元素进行交换,直到全部待排序的元素排完;

代码实现:
//选择排序public void selectSort(int[] array) {if(array.length < 1){return;}for(int i = 0; i<array.length; i++) {//用来存放最小元素下标int min = array[i];//遍历待排序元素for(int j = i; j < array.length; j++) {//符合条件更新最小值if(array[j] < array[min]) {min = j;}}//交换swap(array, i, min);}}private void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}🌼2.2 堆排序
堆排序,根据名字就可以了解到肯定是需要建堆的,而前面也已经讲过了建大(小)根堆的步骤,下面就直接利用现成的大根堆进行讲解;
如果要排升序建立大根堆,排降序建立小根堆,步骤如下:
-
先建立一个大根堆
-
交换第一个和n-i (i=1、2、3、4….)个节点,直到n-i=0时不用再交换
-
进行向下调整,重新构建大根堆结构

代码实现:
public void heapSort(int[] array) {//建立大根堆buildHeap(array);//拿到最后一个节点的下标int len = array.length-1;for(int i = len; i>0; i--) {//交换第一个和最后一个节点值swap(array, 0, i);//向下调整shiftDown(array, 0, i);}} //堆排序//建立大根堆public void buildHeap(int[] array) {int len = array.length;for(int parent = (len-2)/2; parent >= 0; parent--) {shiftDown(array, parent, len);}}//向下调整private void shiftDown(int[] array, int parent, int len) {//求处孩子节点下标int child = (2*parent)+1;while(child < len) {//找到最大的那个孩子节点if(child + 1 < len && array[child] < array[child +1]){child++;}//比较父节点与孩子节点if(array[child] > array[parent]) {swap(array, parent, child);//保证子树的大根堆结构不会被破坏parent = child;child = (2*parent)+1;}else {break;}}}堆排序特性:
- 时间复杂度:O(N*logn),因为每一个元素都需要遍历到,每一次与堆顶元素交换后也都需要进行向下调整;
- 空间复杂度:O(1)
- 稳定性:不稳定
💐3. 交换排序
思想:对序列中的两个值进行比较,根据比较结果来交换这两个值,特点是:升序(降序)较大(较小)的值向尾部移动,值较小(较大)的数据向首部移动;
🌼3.1 冒泡排序

代码实现:
//冒泡排序public void bubbleSort(int[] array) {int len = array.length;boolean flag = true;for(int i = 0; i<len; i++) {for(int j = 0; j<len-i-1; j++) {if(array[j] > array[j+1]) {swap(array, j, j+1);//代码优化,定义一个flagflag = false;}}//如果flag是true,说明遍历一趟下来,没有进行交换,则表示序列此时已经有序了,就不用再遍历剩下的元素了if(flag) {return;}}}
冒泡排序特性:
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
🌼3.2 快速排序
思想:从待排序的序列中任取一个元素作为基准值,然后遍历这个序列,让每个元素都与基准值比较,最后这个序列会根据基准分为两个左右子序列,左子序列中所有的值都比基准小,右子序列中所有的值都比基准大,然后再分别对两个子序列进行分割,最后序列就会变成有序
//快速排序public void quick_sort(int[] array) {//定义左边界和右边界int left = 0;int right = array.length-1;//进行快速排序quickSort(array, left, right);}private void quickSort(int[] array, int left, int right) {//出口为左右边界相等时或右边界小于左边界if(right - left <=1) {return;}//求基准,此时序列会分为左右两个子序列//求基准的方法分为三种int div = partion(array);//分割成功后,根据div分为左右两部分[left, div] 和 [div+1, right]//递归[left, div]quickSort(array, left, div);//递归[right, div+1]quickSort(array, div+1, right);}
以上就是快速排序的模板,有点类似与二叉树的遍历,重点就是求基准的方法,下面介绍三种求基准的方法;
- Hoare法

代码实现:
private int hoare(int[] array, int left, int right) {//记录基准值int key = array[left];//记录基准值下标int pos = left;while(left < right){//寻找比基准值小的元素while(left < right && array[right] >= key) {right--;}//寻找比基准值大的元素while(left < right && array[left] <= key) {left++;}//交换swap(array, left, right);}//根据基准分割成两个子序列swap(array, left, pos);return left;}
-
挖坑法

代码实现:
//挖坑法private int digHole(int[] array, int left, int right) {//存储基准值int key = array[left];while(left < right) {//寻找比基准小的元素while(left < right && array[right] >= key) {right--;}//将left坑填上array[left] = array[right];//寻找比基准值大的元素while(left < right && array[left] <= key) {left++;}//将right坑填上array[right] = array[left];}array[left] = key;return left;} -
前后指针法

代码实现
private int twoPointer(int[] array, int left, int right) {int pre = left;int cur = pre+1;while(cur < array.length){if(array[cur]<array[left] && array[++pre] != array[cur]) {swap(array, cur, pre);}cur++;}swap(array, left, pre);return pre;}
注意点:
如果利用快速排序的方法对十万个有序的数据进行排序,就造成了栈溢出,因为,如果本来就是升序的话,这颗二叉树就是一颗单支树,而采用快速排序时,是要进行递归的,每一次递归都是需要在栈上开辟空间的,造成了时间复杂度是 O(n^2), 空间复杂度是 O(n), 所以就会遭成栈溢出:


🌼3.2.1 快速排序优化
下面介绍对快速排序进行优化,为了防止栈溢出,就要减少递归次数, 如果要减少递归次数就要降低树的高度,步骤为:

- 利用三数取中法找key

private void quickSort(int[] array, int left, int right) {//出口为左右边界相等时或右边界小于左边界if(right - left <=1) {return;}//三数取中int mid = midOfThree(array, left, right);//和第一个交换swap(array, left, mid);//求基准,此时序列会分为左右两个子序列//求基准的方法分为三种int div = hoare(array, left, right);//int div = digHole(array, left, right);//int div = twoPointer(array, left, right);//分割成功后,根据div分为左右两部分[left, div] 和 [div+1, right]//递归[left, div]quickSort(array, left, div);//递归[right, div+1]quickSort(array, div+1, right);}private int midOfThree(int[] array, int left, int right) {//找中间值int mid = (right- left)/2+left;//查找第二大数字if(array[left] < array[right]) {//情况1: 5 3 9if(array[mid] < array[left]) {return left;}else if(array[mid] > array[right]) {//情况2:3 9 5return right;}else {return mid;}}else {//情况1:5 9 3if(array[mid] > array[left]) {return left;}else if(array[mid] < array[right]) {//情况2:9 3 5return right;}else {return mid;}}}

虽然利用三数取中法采用了降低树的高度,但是很可能还会造成栈溢出,但是如果在其他的编译器上可能就能跑过,一个原因是IDEA默认的栈空间比较小,解决方法是可以修改IDEA默认的栈空间大小:



另一个原因是对于三数取中后代码还可以进行优化:
上述三数取中法是防止出现单支树而导致栈溢出情况,从而通过降低树的高度进行解决,但是例如一下这种情况:

2.当递归到小区间时可以采用插入排序
当递归到小区间时,序列已经趋于有序了,而插入排序在序列趋于有序的情况下效率最高,所以在递归到小区间时,可以采用插入排序;

if(right - left + 1 <= 15) {//采用插入排序insertOfRange(array, left, right);return;}public void insertOfRange(int[] array, int start, int end) {//定义i遍历每一个元素//对区间内的元素进行插入排序for(int i = start+1; i<= end; i++) {//定义j遍历i前面的元素int j = i-1;//定义关键码key保存i对应的值int key = array[i];for(; j>=0; j--) {//符合条件进行移动if(array[j] > key) {array[j+1] = array[j];}else {break;}}//最后将key插入array[j+1] = key;}}
🌼3.2.2 快速排序非递归

代码:
public void quickSortNor(int[] array, int left, int right) {Stack<Integer> stack = new Stack<>();//寻找一次基准int pivot = digHole(array, left, right);//判断左边区间是否只有一个元素if(pivot-1 > left){//表示左区间不止一个元素stack.push(left);stack.push(pivot-1);}if(pivot+1 < right) {//表示右区间不止一个元素stack.push(pivot+1);stack.push(right);}//弹出栈中元素while(!stack.isEmpty()) {//弹出左边界和右边界right = stack.pop();left = stack.pop();//再次找基准pivot = digHole(array, left, right);//判断左边区间是否只有一个元素if(pivot-1 > left){//表示左区间不止一个元素stack.push(left);stack.push(pivot-1);}if(pivot+1 < right) {//表示右区间不止一个元素stack.push(pivot+1);stack.push(right);}}}

快速排序特性:
- 时间复杂度:O(n*logn),因为快排对每一个元素都要操作,因为每一个元素都需要logn的时间复杂度,所以n个元素就是n *logn
- 空间复杂度:O(logn)
- 稳定性:不稳定
💐4. 归并排序
🌼4.1 基本思想
归并排序它是运用了分支算法的思想:分而治之,将一个序列分割成两份,对每一份再进行分割,一直分割到不能再分割,再进行合并;请看图解:

代码示例:
//归并排序public void mergeSort(int[] array, int left, int right) {//递归出口if(left >= right) {return;}//求中间位置元素int mid = (right - left) / 2 + left;//递归左序列mergeSort(array, left, mid);//递归右序列mergeSort(array, mid+1, right);//合并两个序列,使序列有序merge(array, left, right, mid);}private void merge(int[] array, int left, int right, int mid){//申请一个数组用来存放合并后的元素int[] tmp = new int[right-left+1];//定义两个序列的首位置int start1 = left;int start2 = mid+1;//记录新数组中待存放元素的下标int index = 0;//合并序列中的元素while(start1 <= mid && start2 <= right){if(array[start1] < array[start2]) {tmp[index++] = array[start1++];}else {tmp[index++] = array[start2++];}}//检查哪一个序列没有遍历完while(start1 <= mid) {tmp[index++] = array[start1++];}while(start2 <= right) {tmp[index++] = array[start2++];}//将tmp的元素再移动到array中for(int i = 0; i<tmp.length; i++) {//i+left 定位到当前的序列的首位置,因为序列被分割后,每一个子序列的首位置都不一样array[i+left] = tmp[i];}}

归并排序特性:
- 时间复杂度:O(n* logn)
- 空间复杂度:O(n),因为需要常见新数组
- 稳定性:稳定
💐6. 海量数据进行排序
问题:如果有1G的内存,但是要对100G的的数据进行排序,应该怎么办?
解答:
因为100G的数据在内存中放不下,所以要利用外部排序,就像归并排序
外部排序:在磁盘等外部存储上进行的排序
1、将100G数据分为200份小文件,每个文件都是512M

2.将每一份文件都放进内存中进行排序

3、进行二路归并,合并200份文件

相关文章:

【数据结构】七大排序
文章目录 💐1. 插入排序🌼1.1 直接插入排序🌼1.2 希尔排序 💐2. 选择排序🌼2.1 直接选择排序🌼2.2 堆排序 💐3. 交换排序🌼3.1 冒泡排序🌼3.2 快速排序🌼3.2.…...

区块链实验室(24) - FISCO网络重构
若干次实验以后,FISCO网络中100个节点堆积了不少交易记录,消耗不少磁盘空间,见下图所示,100个节点累计消耗了10G空间。 观察每个节点的磁盘消耗,以node88为例,消耗了107MB,见下图所示。在该节点…...
AI智能写作工具有哪些?永久免费的AI智能写作工具你使用过吗?
AI智能写作是指借助人工智能技术,计算机程序可以自动生成各种文本内容,包括新闻报道、广告文案、科技文章、小说等等。这些AI写作工具通过大数据和深度学习模型,能够分析和模仿人类的写作风格,生成高质量的文本,甚至有…...

23.8.15 杭电暑期多校9部分题解
1002 - Shortest path 题目大意 对于一个数 x x x,可以进行以下三种操作: 1.将 x x x 变成 2 ∗ x 2*x 2∗x 2.将 x x x 变成 3 ∗ x 3*x 3∗x 3.将 x x x 变成 x 1 x1 x1 给定一个数 n n n,问最少操作几次才能将 1 1 1 变成…...

四个BY的区别 HIVE中
在Hive中,有四个BY比较:Order By、Sort By、Distribute By和Cluster By。 Order By是全局排序,只有一个Reducer。它可以按照升序(ASC)或降序(DESC)对结果进行排序。Order By子句通常用在SELECT语…...

计时函数与float32 float16 int8 数据转换
个人整理常用 部分来自 ncnn 计时函数 // window 平台 #include <windows.h>double get_current_time() {LARGE_INTEGER freq; // 频率LARGE_INTEGER pc; // 计数QueryPerformanceFrequency(&freq);QueryPerformanceCounter(&pc);return pc.QuadPart * 1000…...

自身免疫疾病诊断原料——博迈伦
自身免疫疾病是一类由免疫系统攻击正常组织和器官而引起的疾病。为了准确地诊断和监测自身免疫疾病,需要使用特定的诊断原料来进行实验室检测。这些诊断原料主要包括抗体试剂、抗原试剂和试剂盒等。 抗体试剂是用于检测和定量分析体内免疫系统产生的抗体的化学试剂。…...
cpu温度监测 Turbo Boost Switcher Pro for mac最新
Turbo Boost Switcher Pro是一款Mac电脑上的应用程序,旨在帮助用户控制和管理CPU的Turbo Boost功能。Turbo Boost是Intel处理器中的一项技术,可以在需要更高性能时自动提高处理器的频率。然而,这可能会导致电池消耗更快和温度升高。 以下是T…...

spring 请求 出现实体类大小写不一致 出现的问题
目录 1.问题背景 2.解决方法 但是会存在返回的既有大写也有小写的问题,需要在get方法也添加对应的注解 3.相关资料 1.问题背景 因数据库某字段存储的为json 格式,且数据库字段要求都有客户指定,因为该功能需要和其他项目进行对接。然后出现…...

zaabix实现对nginx监控
本文使用监控模板net.tcp.listen[port]实现监听端口 实验环境: 首先搭建好zabbix-server ,zabbix-agenthttps://mp.csdn.net/mp_blog/creation/editor/132622769?spm1001.2014.3001.9457 而后在zabbix-agent主机上下载一个nginx 登录zabbix网站创建主…...

基于AI视觉的表面缺陷检测设备优势显著,加速制造业数智化转型
作为生产制造过程中不可缺少的一步,表面缺陷检测广泛应用于工业领域,包括3C电子、芯片半导体、食品医药、木材等行业。但随着智能化进程加快,制造工厂生产线的质量检测压力加剧,传统人工表面缺陷检测已经无法满足当前社会较高的检…...
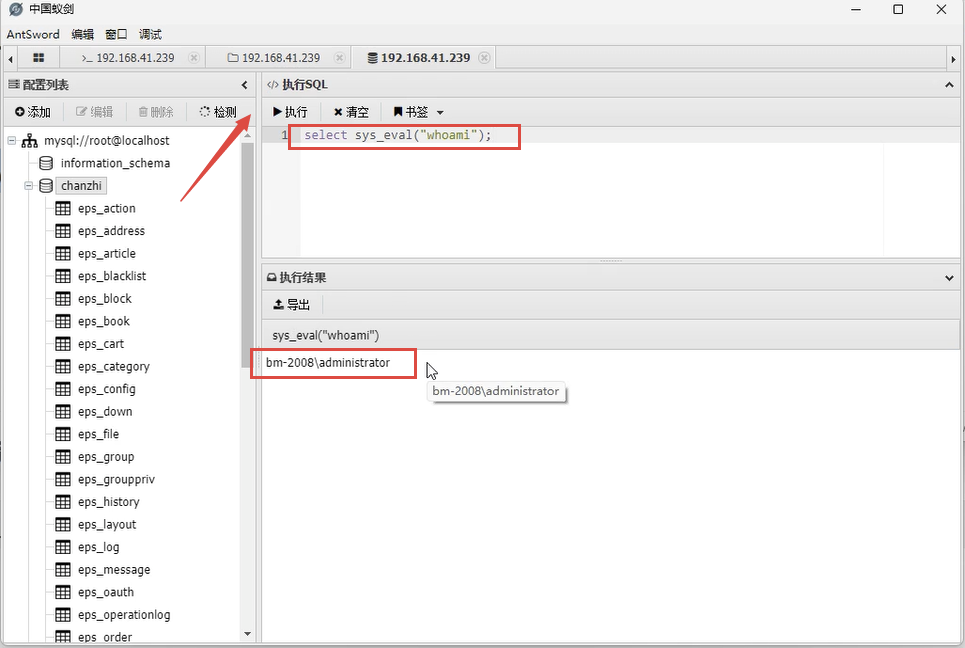
操作系统权限提升(二十六)之数据库提权-MySQL UDF提权
MySQL UDF提权 MySQL介绍 MySQL是最流行的开放源码SQL数据库管理系统,相对于Oracle,DB2等大型数据库系统,MySQL由于其开源性、易用性、稳定性等特点,受到个人使用者、中小型企业甚至一些大型企业的广泛欢迎,MySQL具有…...

基于 IntelliJ 的 IDE 将提供 Wayland 支持
导读对于使用 IntelliJ 开发环境的用户,JetBrains 一直致力于提供原生 Wayland 支持。 JetBrains 正在致力于为基于 IntelliJ 的 IDE 提供 Wayland 支持,以增强 Linux 桌面体验以及在 Windows Subsystem for Linux 下运行。 Wayland 支持功能尚未完成&…...
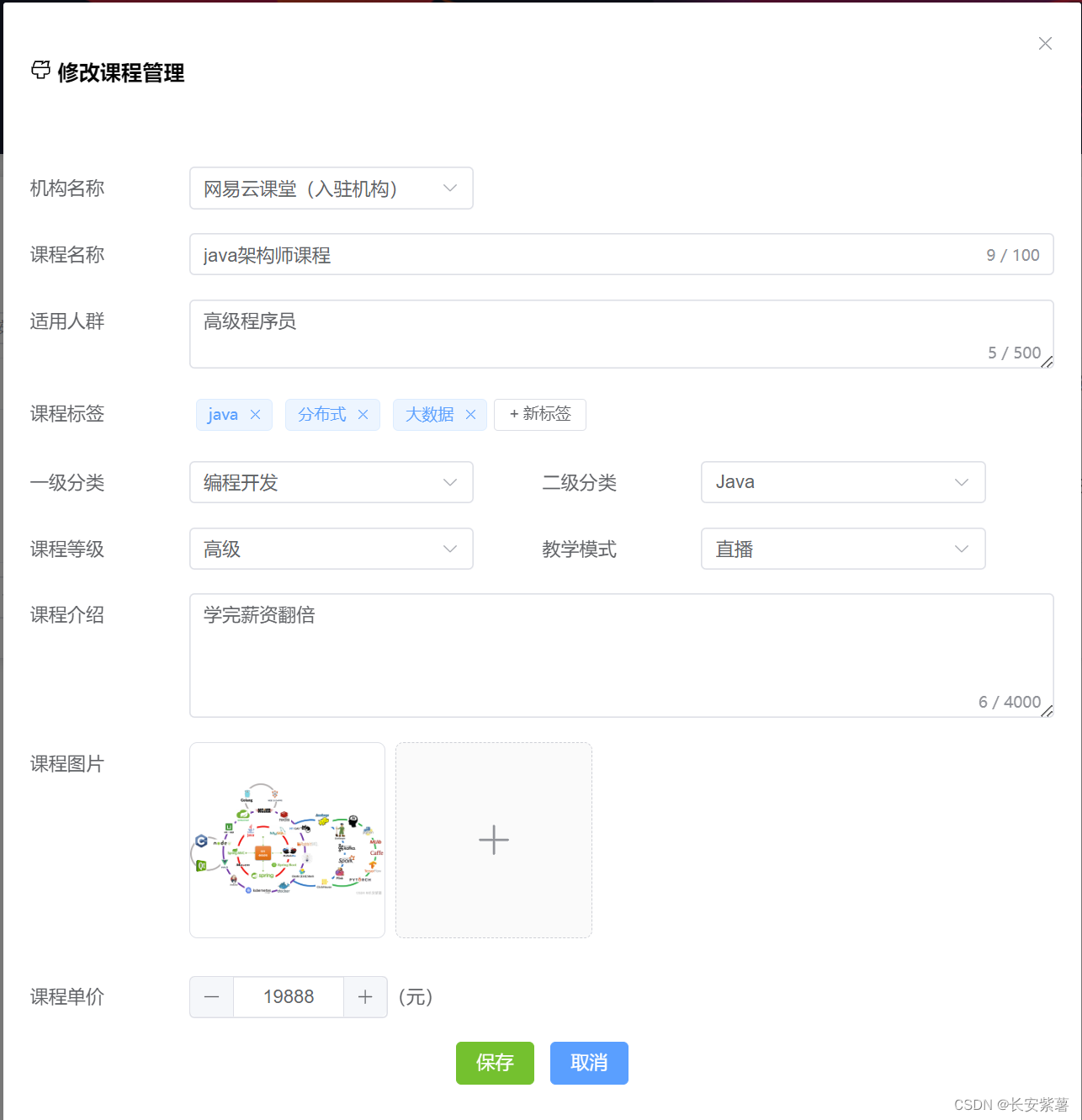
誉天在线项目~ElementPlus Tag标签用法
效果图 页面展现 <el-form-item label"课程标签"><el-tagv-for"tag in dynamicTags":key"tag"class"mx-1"closable:disable-transitions"false"close"handleClose(tag)"style"margin:5px;">…...

iText实战--Table、cell 和 page event
5.1 使用表和单元格事件装饰表 实现PdfPTableEvent 接口 实现PdfPCellEvent 接口 合并表格和单元格事件 5.2 基本构建块的事件 通用块(Chunk)功能 段落(Paragraph)事件 章节(Chapter)和 区域(…...
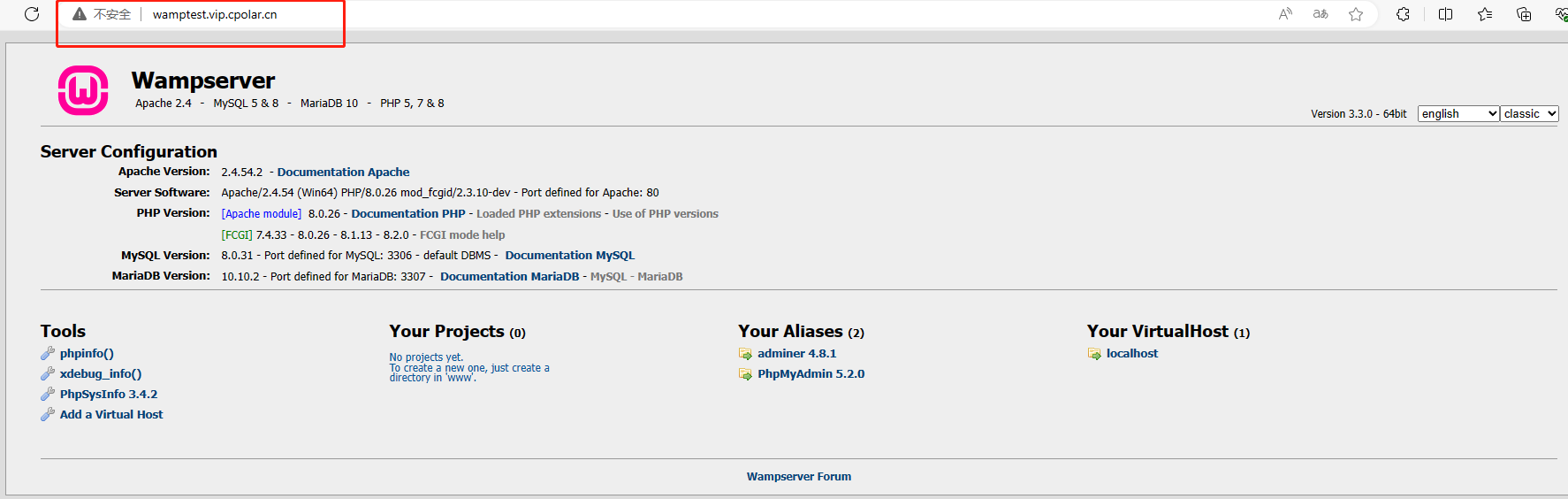
WampServer下载安装+cpolar内网穿透实现公网访问本地服务【内网穿透】
文章目录 前言1.WampServer下载安装2.WampServer启动3.安装cpolar内网穿透3.1 注册账号3.2 下载cpolar客户端3.3 登录cpolar web ui管理界面3.4 创建公网地址 4.固定公网地址访问 前言 Wamp 是一个 Windows系统下的 Apache PHP Mysql 集成安装环境,是一组常用来…...

Elasticsearch 入门 索引、分词器
term, match_phrase, match查询 参考 ElasticSearch match, match_phrase, term的区别 term是对输入不分词,进行全文索引查询。存储时是否启用分词器,会影响查询效果match_phase对输入分词,但要求查询时将每个term都搜到,且顺序…...

Android NDK 中有导出 sp智能指针吗?如果没有,可以用什么方法代替 android::sp 智能指针
Android NDK 中有导出 sp智能指针吗?如果没有,可以用什么方法代替 android::sp 智能指针 Author: Lycan Note: 以下问题解答通过大模型生成,主要用于个人学习和备忘,仅供参考,若有错误或者侵权,请联系我修…...

网络爬虫-----爬虫的分类及原理
目录 爬虫的分类 1.通用网络爬虫:搜索引擎的爬虫 2.聚焦网络爬虫:针对特定网页的爬虫 3.增量式网络爬虫 4.深层网络爬虫 通用爬虫与聚焦爬虫的原理 通用爬虫: 聚焦爬虫: 爬虫的分类 网络爬虫按照系统结构和实现技术&#…...

uniapp级联菜单地点区域使用label值,web端el-cascader绑定的value
效果图 一、uniapp uniapp级联菜单地点区域使用label值 1.ui使用 <uni-forms-item label="地址" name="userArea" required><view class="" style="height: 100%;display: flex;align-items: center;">...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
