岭回归与LASSO回归:解析两大经典线性回归方法
文章目录
- 🍋引言
- 🍋岭回归(Ridge Regression)
- 🍋实战---岭回归
- 🍋LASSO回归(LASSO Regression)
- 🍋实战---LASSO回归
- 🍋岭回归和LASSO哪个更容易是直线
- 🍋岭回归与LASSO回归的应用
- 🍋L1正则化和L2正则化
- 🍋偏差和方差
🍋引言
在机器学习和统计建模中,回归分析是一项重要的任务,用于预测一个或多个因变量与一个或多个自变量之间的关系。在这个领域中,有许多回归方法可供选择,其中岭回归和LASSO回归是两种经典的线性回归技术。在本文中,我们将深入探讨这两种方法的原理、应用和优缺点,帮助您更好地理解它们在实际问题中的作用。
🍋岭回归(Ridge Regression)
岭回归,又称L2正则化,是一种用于解决多重共线性问题的线性回归技术。多重共线性是指自变量之间存在高度相关性的情况,这会导致普通最小二乘法(OLS)估计的不稳定性,使得模型的预测性能下降。岭回归通过在损失函数中添加一个正则化项来解决这个问题,其数学表达式如下: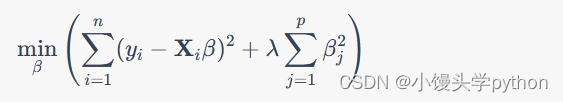
其中, y i y_i yi 是观测值, X i \mathbf{X}_i Xi 是自变量矩阵, β \beta β 是待估计的回归系数, λ \lambda λ 是正则化参数,用于控制正则化的强度。岭回归通过增加 β j \beta_j βj的平方和来限制回归系数的大小,从而减少多重共线性对估计结果的影响。
岭回归的优点包括:
- 改善多重共线性问题。
- 稳定的估计结果,不容易受到异常值的影响。
- 可以处理高维数据集,避免过拟合。
然而,岭回归也有一些缺点,例如它不能自动选择重要的特征,需要手动调整正则化参数 λ \lambda λ,并且可能不适用于稀疏数据集。
🍋实战—岭回归
首先我们假设一组数据
import numpy as np
import matplotlib.pyplot as pltnp.random.seed(666)
x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5 * x + 3 + np.random.normal(0,1,size=100)plt.scatter(X,y)
plt.show()
运行结果如下
接下来我们导入我们需要的一些库
from sklearn.preprocessing import PolynomialFeatures,StandardScaler
from sklearn.pipeline import Pipeline # 管道
from sklearn.linear_model import LinearRegression,Ridge,Lasso # 岭回归和LASSO回归
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
为了方便读者理解,这里我将每个库进行一些说明
-
sklearn.preprocessing:这个库是scikit-learn(通常被称为sklearn)的一部分,用于数据预处理。其中的PolynomialFeatures类可以用来生成多项式特征,将原始特征转换为高次幂的特征,以帮助模型拟合非线性关系。这对于处理非线性问题非常有用。StandardScaler类用于标准化数据,即将数据进行均值为0、方差为1的缩放,以确保特征在相同的尺度上。
-
sklearn.pipeline:Pipeline是一种机器学习中用于构建和管理多个数据处理和模型构建步骤的工具。它允许将多个数据处理步骤串联在一起,形成一个连续的流程。在您的代码示例中,Pipeline用于将多项式特征生成、数据标准化和线性回归(或其他回归算法)的步骤组合在一起,使其可以一次性执行。
-
sklearn.linear_model:这个库包含了各种线性回归模型的实现。这里面提到了LinearRegression、Ridge和Lasso。这些模型用于进行线性回归分析。具体来说,LinearRegression是标准的线性回归模型,Ridge是岭回归模型,Lasso是LASSO回归模型。这些模型用于建立线性关系模型,其中目标是拟合自变量和因变量之间的线性关系,并预测未知数据的因变量值。
-
sklearn.model_selection:这个库提供了用于模型选择和评估的工具。train_test_split函数用于将数据集分成训练集和测试集,以便训练模型和评估其性能。您可以使用此函数将数据划分为两部分,一部分用于训练模型,另一部分用于评估模型的性能。
-
sklearn.metrics:这个库包含了各种用于模型性能评估的指标。在您的代码示例中,您提到了mean_squared_error。这是一个用于回归问题的评估指标,用于度量模型的预测值与实际观测值之间的均方误差。均方误差越小,模型的性能越好。
之后我们需要创建一个多项式回归模型管道,管道的创建方式之前有提过,这里就直接展示
def polynomialRegression(degree):return Pipeline([('poly',PolynomialFeatures(degree)),('std_scaler',StandardScaler()),('lin_reg',LinearRegression())])
之后我们进行分割数据集并且设置随机种子
np.random.seed(666)
X_train,X_test,y_train,y_test = train_test_split(X,y)
接下来我们还是创建一个函数,为了可视化数据
def plot_model(estimator):y_predict = estimator.predict(X_test)print(mean_squared_error(y_test,y_predict))X_plot = np.linspace(-3,3,100).reshape(-1,1)y_plot = estimator.predict(X_plot)plt.scatter(X,y)plt.plot(X_plot,y_plot,color='r')plt.axis([-3,3,-2,6])
这里我进行一个代码的解释说明,我们定义了一个plot_model函数,这个函数的参数是一个已经训练好的模型,之后打印一个均方误差,用于为了测试预测性能;之后就是预测并且绘制图像了
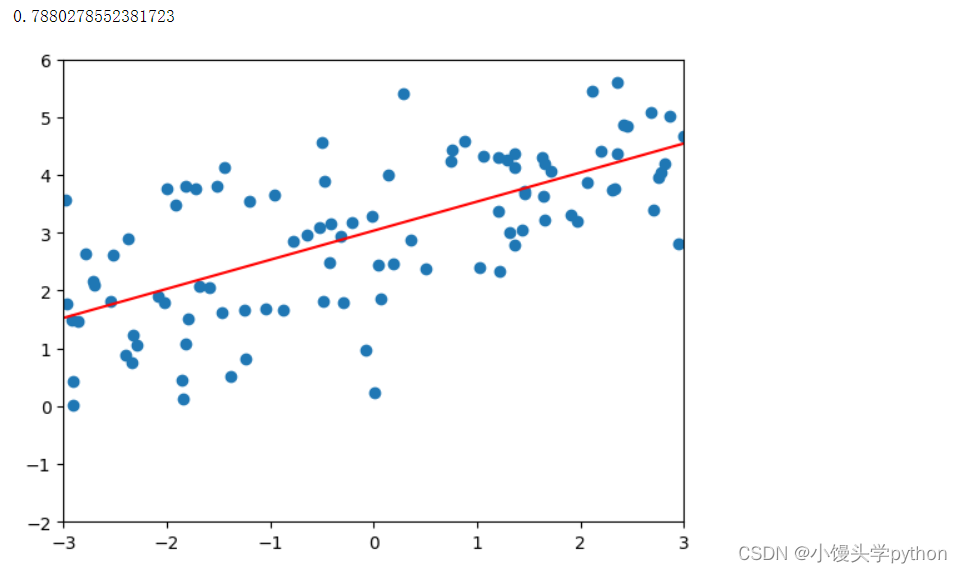
之后我们就可以进行拟合了,这里采用的是多项式回归模型
poly_reg = polynomialRegression(1)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
第一行定义了一个polynomialRegression类,参数为1代表是一阶多项式;之后使用fit进行训练,最后将训练好的模型传入到plot_model函数中
运行结果如下
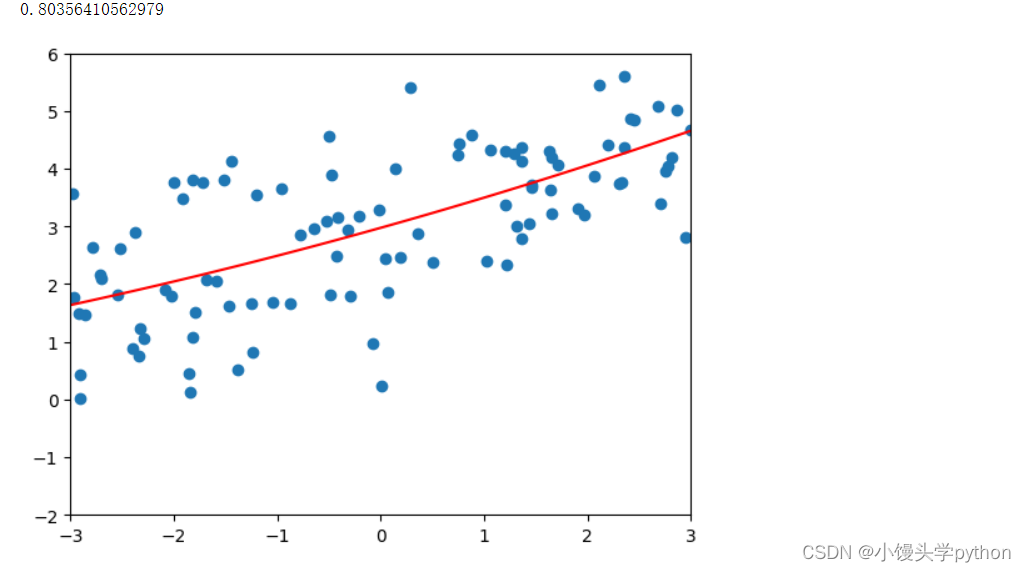
接下来我们再以二阶多项式和二十阶多项式进行绘制图像
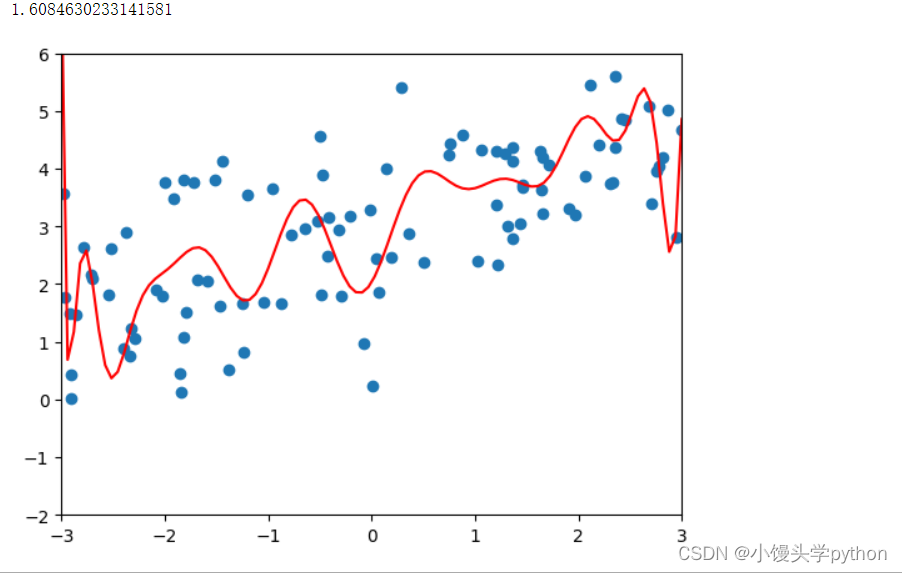
接下来我们重新定义管道,使用岭回归
def polynomialRidgeRegression(degree,alpha):return Pipeline([('poly',PolynomialFeatures(degree)),('std_scaler',StandardScaler()),('lin_reg',Ridge(alpha=alpha))])
之后我们进行拟合
poly_reg = polynomialRidgeRegression(20,0.0001)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
运行结果如下
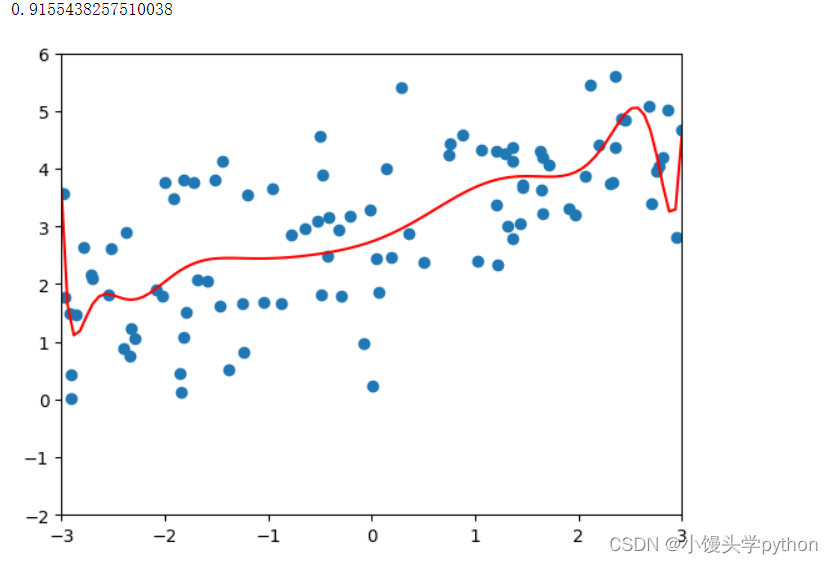
之后我们再重新修改一下参数
poly_reg = polynomialRidgeRegression(20,1000)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
运行结果如下
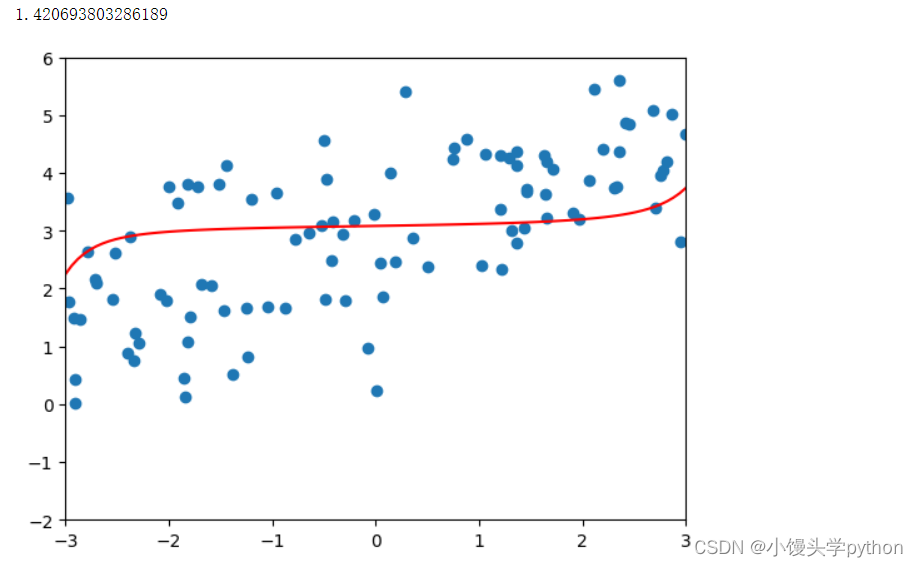
从均方误差来看,有点正则过头了
那么如果 λ \lambda λ再大点呢
poly_reg = polynomialRidgeRegression(20,100000)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
运行结果如下
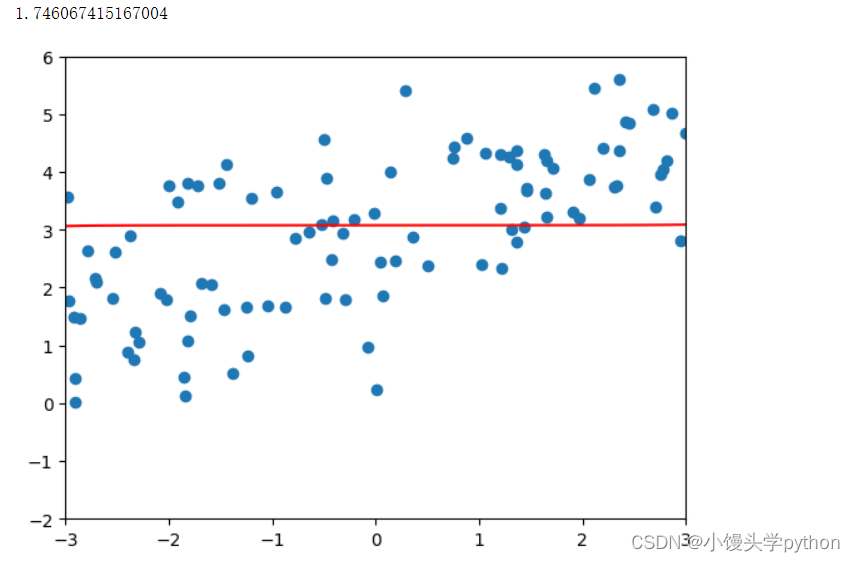
会发现几乎趋近于一条直线了。我们再来看看LASSO回归
🍋LASSO回归(LASSO Regression)
LASSO回归,又称L1正则化,是另一种处理多重共线性问题的线性回归方法。与岭回归不同,LASSO回归在损失函数中添加的正则化项是回归系数的绝对值之和,其数学表达式如下: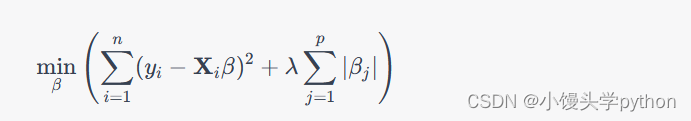
与岭回归相比,LASSO回归有以下特点:
- LASSO回归具有特征选择的能力,它可以将某些回归系数缩减至零,从而自动选择重要的特征。
- 可以用于稀疏数据集的建模。
- LASSO回归的正则化路径可以帮助选择最优的正则化参数 λ \lambda λ。
然而,LASSO回归也有一些缺点,例如当自变量之间高度相关时,它可能随机选择其中一个自变量并将其系数设为零,不稳定性较高。
🍋实战—LASSO回归
与岭回归类似,这里就不一一赘述了
def polynomialLsssoRegression(degree,alpha):return Pipeline([('poly',PolynomialFeatures(degree)),('std_scaler',StandardScaler()),('lin_reg',Lasso(alpha=alpha))])
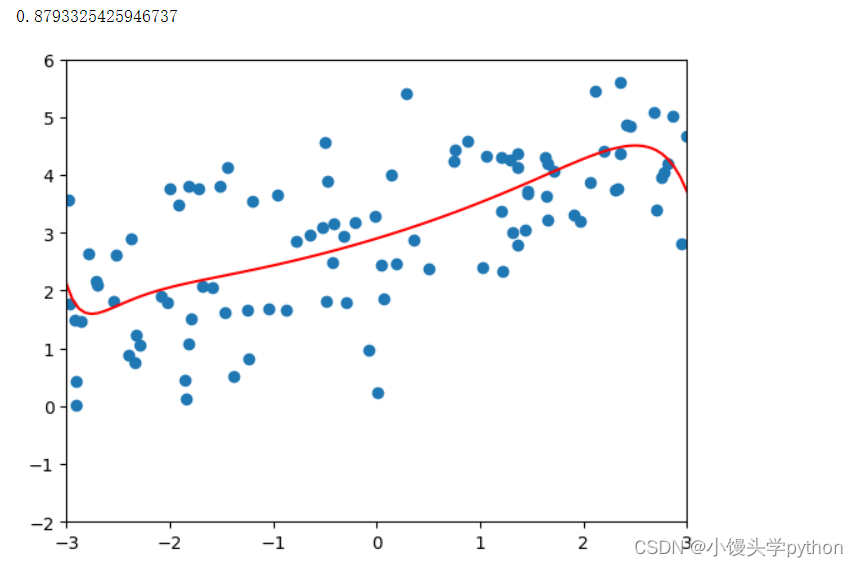
poly_reg = polynomialLsssoRegression(20,0.01)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
运行结果如下
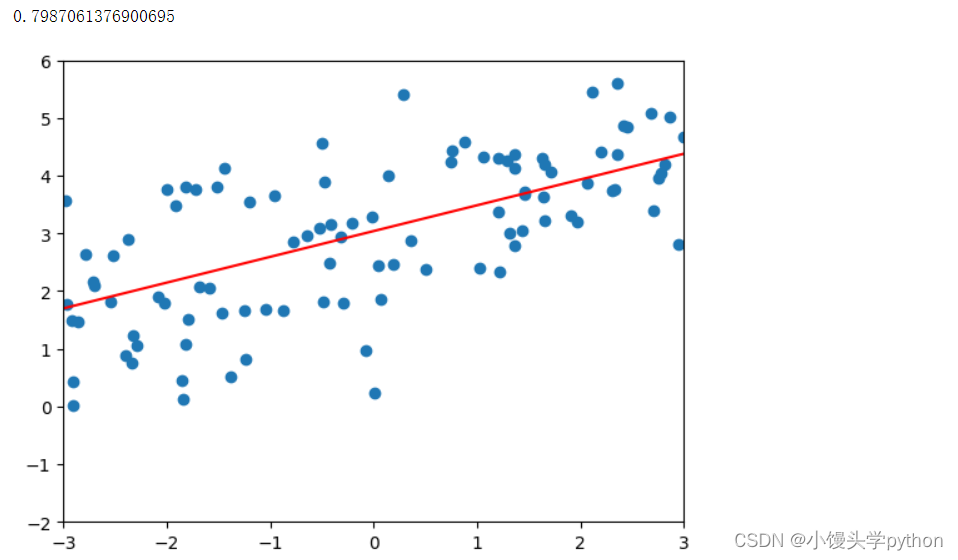
poly_reg = polynomialLsssoRegression(20,0.1)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
运行结果如下
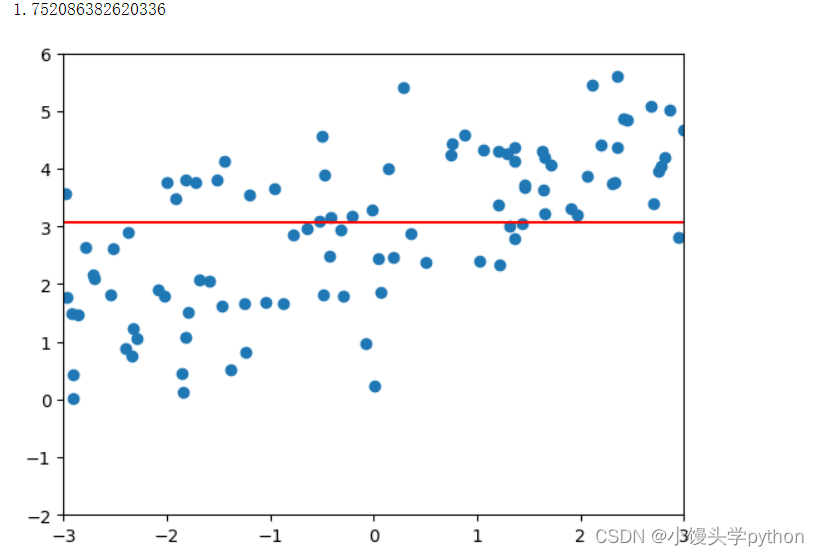
poly_reg = polynomialLsssoRegression(20,1)
poly_reg.fit(X_train,y_train)
plot_model(poly_reg)
运行结果如下
🍋岭回归和LASSO哪个更容易是直线
-
岭回归:
岭回归引入的正则化项是L2正则化,它是回归系数的平方和。这个正则化项的作用是限制回归系数的大小,使它们不能过大。因此,岭回归有助于处理多重共线性问题,同时也可以防止过拟合。由于L2正则化是平方和的形式,所以它倾向于平滑回归系数,使它们趋向于均匀分布,不太容易生成稀疏模型。
岭回归的拟合曲线通常是平滑的,因为它在正则化项中对所有回归系数都施加了一定的约束,不容易将某些系数压缩至零。这意味着岭回归的模型通常不会是严格的直线,而是某种形式的平滑曲线。
-
LASSO回归:
LASSO回归引入的正则化项是L1正则化,它是回归系数的绝对值之和。这个正则化项的作用是促使一些不重要的回归系数变为零,实现自动特征选择。因此,LASSO回归可以生成稀疏模型,即只保留一部分重要的特征。
由于L1正则化的性质,LASSO回归的拟合曲线可能是分段线性的,也就是说,在某些特征上,回归系数为零,因此模型会生成严格的直线。这使得LASSO回归在某些情况下更容易生成直线模型。
🍋岭回归与LASSO回归的应用
这两种回归方法在许多领域都有广泛的应用,包括金融、医学、自然语言处理和工程等。具体应用如下:
- 金融领域:用于预测股票价格、房地产市场分析和信用评分模型。
- 医学领域:用于疾病预测、药物研发和医疗成本估计。
- 自然语言处理:用于文本分类、情感分析和机器翻译等。
- 工程领域:用于预测材料强度、机械故障检测和质量控制。
🍋L1正则化和L2正则化
L1正则化和L2正则化都是用于线性回归等机器学习模型中的正则化技术,它们的作用是防止模型过拟合,提高模型的泛化能力。它们的区别在于正则化项的形式和影响:
L1正则化(Lasso正则化):
-
正则化项形式:L1正则化引入的正则化项是回归系数的绝对值之和。在数学上,它是回归系数的L1范数。
-
效果:L1正则化具有稀疏性质,即它有助于将某些不重要的特征的回归系数缩减至零,从而实现特征选择。这意味着L1正则化可以用来降低模型的复杂性,使模型更简单且易于解释。
-
稀疏性:L1正则化使得一些回归系数变得精确地等于零,因此可以生成稀疏模型。这对于高维数据集中的特征选择非常有用。
-
适用情况:L1正则化通常用于具有大量特征的数据集,并且希望自动选择最重要的特征的情况下。它也适用于处理多重共线性问题,但不如L2正则化那样强烈。
L2正则化(Ridge正则化):
-
正则化项形式:L2正则化引入的正则化项是回归系数的平方和。在数学上,它是回归系数的L2范数。
-
效果:L2正则化有助于防止模型的回归系数过大,从而降低模型对训练数据的过拟合风险。它不具备L1正则化的稀疏性质,通常不会将回归系数精确地压缩至零,而是使其趋向于较小的值。
-
平滑性:L2正则化倾向于生成平滑的回归系数,使模型更加稳定。它对多重共线性问题有较好的处理能力,可以减小相关特征之间的系数差异。
-
适用情况:L2正则化通常用于处理多重共线性问题或者在模型需要保留大部分特征的情况下,但希望限制回归系数的大小以提高模型的泛化能力。
🍋偏差和方差
偏差和方差是统计学和机器学习中两个重要的概念,用于评估模型的性能和泛化能力。它们通常一起讨论,因为它们在模型的复杂性和性能之间存在权衡关系。
-
偏差(Bias):
偏差是指模型的预测值与真实值之间的差距,即模型对问题的错误偏向。
当模型具有高偏差时,意味着它过于简单,无法捕捉数据中的复杂模式。这种情况下,模型可能会欠拟合,导致在训练数据和测试数据上都表现不佳。
通常来说,增加模型的复杂度(例如增加特征数量或增加模型参数)可以减小偏差,使其更能适应训练数据,但可能增加方差。 -
方差(Variance):
方差是指模型对于不同训练数据集的敏感性,即模型在不同数据集上的预测结果波动程度。
当模型具有高方差时,意味着它过于复杂,对训练数据过度拟合。这种情况下,模型在训练数据上表现很好,但在测试数据上可能表现不佳。
减小模型复杂度可以减小方差,使其更加稳定,但可能增加偏差。

挑战与创造都是很痛苦的,但是很充实。
相关文章:

岭回归与LASSO回归:解析两大经典线性回归方法
文章目录 🍋引言🍋岭回归(Ridge Regression)🍋实战---岭回归🍋LASSO回归(LASSO Regression)🍋实战---LASSO回归🍋岭回归和LASSO哪个更容易是直线🍋…...
数学建模——微分方程介绍
一、基础知识 1、一阶微分方程 称为一阶微分方程。y(x0)y0为定解条件。 其常规求解方法: (1)变量分离 再两边积分就可以求出通解。 (2)一阶线性求解公式 通解公式: 有些一阶微分方程需要通过整体代换…...

Minio入门系列【7】Spring Boot集成Minio
1 前言 之前介绍了如何使用Minio提供的JAVA SDK进行上传和下载文件,在此基础上,我们可以使用spring boot集成Minio JAVA SDK,添加自动配置、装配、客户端管理等功能,简化开发 2 Spring Boot集成Minio 2.1 环境搭建 首先我们搭…...
)
抖音视频下载.py(23年9月份可用)
声明:仅供学习交流使用!!! 抖音无水印视频下载; 首先登录抖音网页端 打开要下载的视频userId 然后编码实现下载 最后是完整代码,拿走就能用那种: # _*_ coding:utf-8 _*_import json import requests import time import randomheaders = """Accept: a…...

项目基本搭建流程
项目创立:webapp 设置maven 的和settings.xml 的地址 手动建立java文件夹和resource文件夹 一.分层 二.使用generator 来自动建立实体类dao 和dao接口,存放sql文件的xml;并复制到项目中(路径可能可以直接设置) 三. 配置文件&…...
学习pytorch11 神经网络-非线性激活
神经网络-非线性激活 官网文档常用1 ReLUinplace 常用2 Sigmoid 代码logs B站小土堆学习pytorch视频 非常棒的up主,讲的很详细明白 官网文档 https://pytorch.org/docs/stable/nn.html#non-linear-activations-weighted-sum-nonlinearity 常用1 ReLU 对输入做截断…...
Jenkins学习笔记2
Jenkins下载安装: 从清华源开源镜像站上下载jenkins的安装包: 安装的是这个版本。 关于软件的版本,尽量使用LTS,长期支持。 首先是安装openjdk: yum install fontconfig java-11-openjdk[rootlocalhost soft]# java …...

自动化测试:yaml结合ddt实现数据驱动!
在pythonunittestseleniumddt的框架中,数据驱动常见有以下几种方式实现: Csv/txtExcelYAML 本文主要给大家介绍测试数据存储在YAML文件中的使用场景。首先先来简单介绍一下YAML。 1. 什么是YAML 一种标记语言类似YAML,它实质上是一种通用…...
高效管理,轻松追踪——Chrono Plus for Mac任务管理工具
Chrono Plus for Mac是一款专注于任务管理和跟踪的应用程序。它提供了一种直观、清晰的界面,使您能够轻松创建、安排和分类任务。无论是个人项目还是团队合作,Chrono Plus都能为您提供一种有效组织和管理任务的方式。 这个应用程序具有多种强大的功能&a…...

python项目2to3方案预研
目录 官方工具2to3工具安装参数解释基本使用工具缺陷 future工具安装参数解释基本使用工具缺陷 python-modernize工具安装参数解释基本使用工具缺陷 pyupgrade工具安装参数解释基本使用工具缺陷 对比 官方工具2to3 2to3 是Python官方提供的用于将Python 2代码转换为Python 3代…...

MongoDB 是什么和使用场景概述(技术选型)
一、从NOSQL(Not Only SQL)说起 常见的数据库可以分为下面的两种类型: RDBMS(关系型数据库):常见的关系型数据库有 Oracle、DB2、Microsoft SQL Server、Microsoft Access、MySQL;NoSQL(非关系型数据库&a…...

打印 pyspark.sql.dataframe.DataFrame 有哪些列
在 PySpark 中,要打印 pyspark.sql.dataframe.DataFrame 的列,可以使用 columns 属性。以下是一个示例代码: from pyspark.sql import SparkSession# 创建 SparkSession spark SparkSession.builder.getOrCreate()# 假设您的 DataFrame 名称…...

什么是虚拟DOM(Virtual DOM)?它在前端框架中的作用是什么?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 什么是虚拟DOM(Virtual DOM)?⭐ 虚拟DOM 在前端框架中的作用⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦&…...
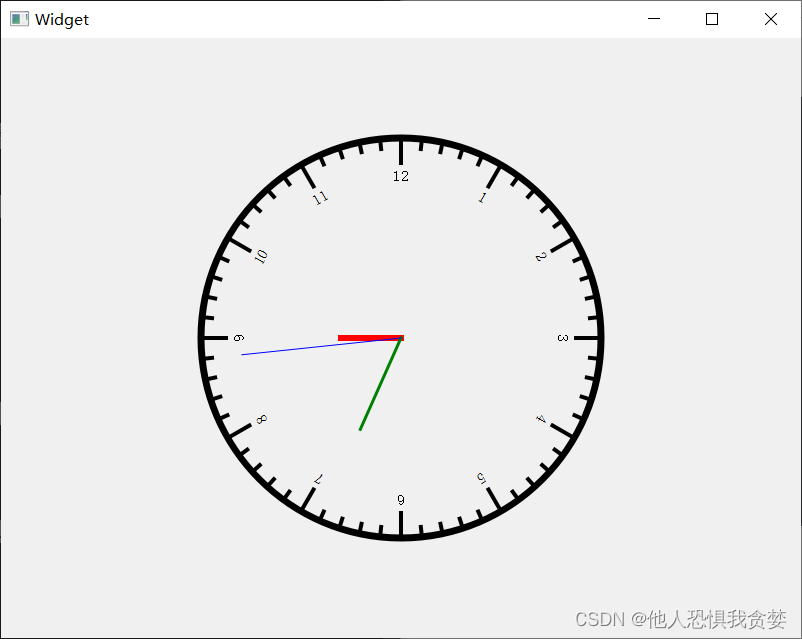
QT实现简易时钟
头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPaintEvent> #include <QDebug> #include <QPainter> #include <QTimerEvent> #include <QTimer> #include <QTime>QT_BEGIN_NAMESPACE namespace Ui { cl…...
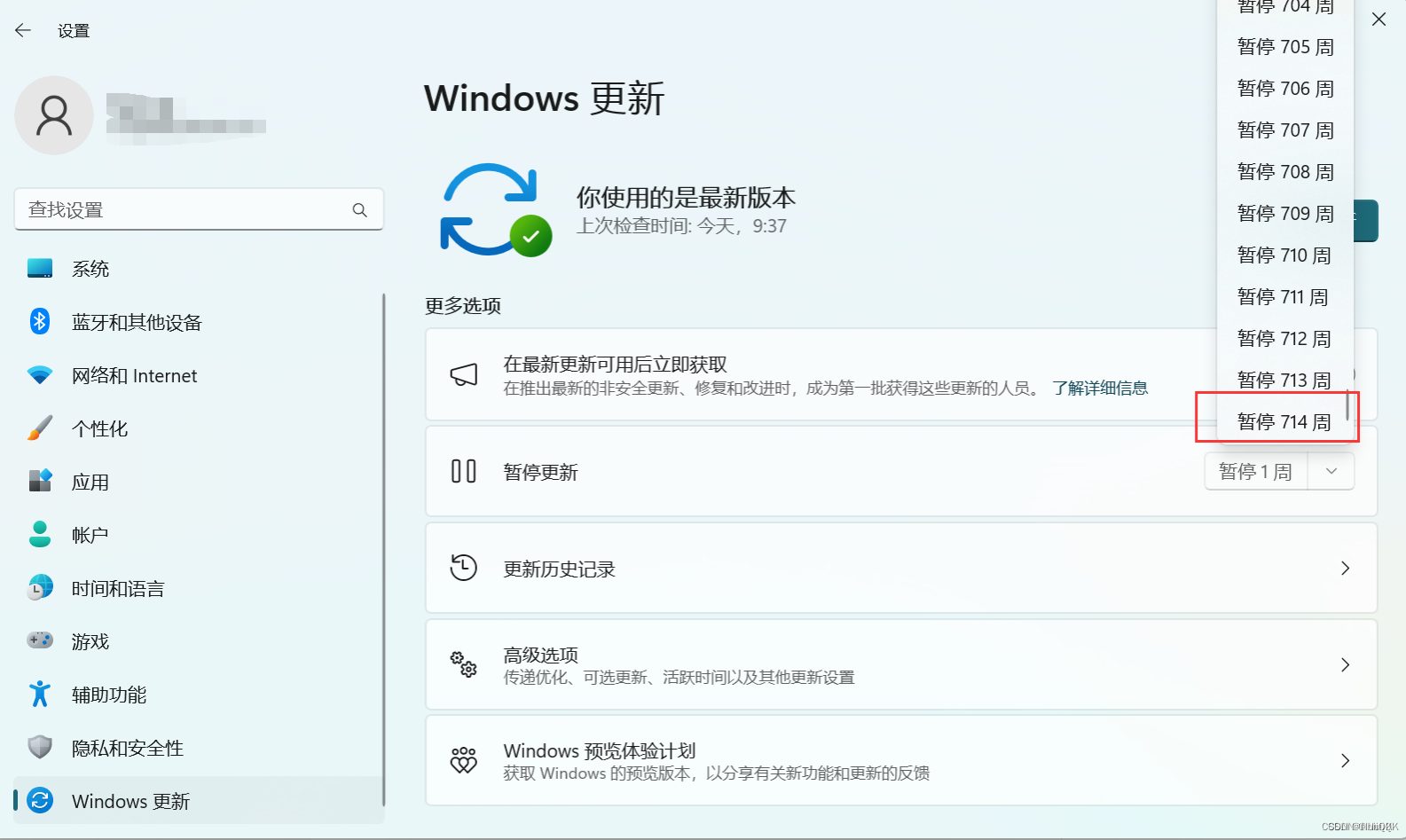
win禁用更新,取消windows更新提示,禁用windows自动更新
取消windows自动更新 前言:跟着我的节奏一步一步点下去,就OK 第一步第二步第三步第四步第五步第六步第七步 新建文件第八步 新增文件名称:FlightSettingsMaxPauseDays第九步 设置暂停更新天数第十步 选中你设置的最大值 前言:跟着…...

倒计时列表实现(小程序端Vue)
//rich-text主要用来将展示html格式的,可以直接使用这个标签 <view class"ptBox" v-for"(item,index) in orderList" :key"index"> <rich-text :nodes"item.limit_time|limitTimeFilter"></rich-text>…...

ContentType:application/x-www-form-urlencoded请求方法遇到的坑【PHP】
有些API要求请求的内容类型为application/x-www-form-urlencoded function requestUrl($url,$datanull,$httpstrue,$methodpost){//1.初始化url$ch curl_init($url);//2.设置相关的参数//字符串不直接输出,进行一个变量的存储curl_setopt($ch, CURLOPT_RETURNTRANSFER, true)…...

RabbitMQ - 死信、TTL原理、延迟队列安装和配置
目录 一、死信交换机 1.1、什么是死信交换机 1.2、TTL 1.2.1、什么是 TTL 1.2.2、通过 TTL 模拟触发死信 二、延迟队列 2.1、什么是延迟队列 2.2、配置延迟队列插件 2.2.1、延迟队列配置 a)下载镜像 b)运行容器 c)刚刚设定的Rabb…...
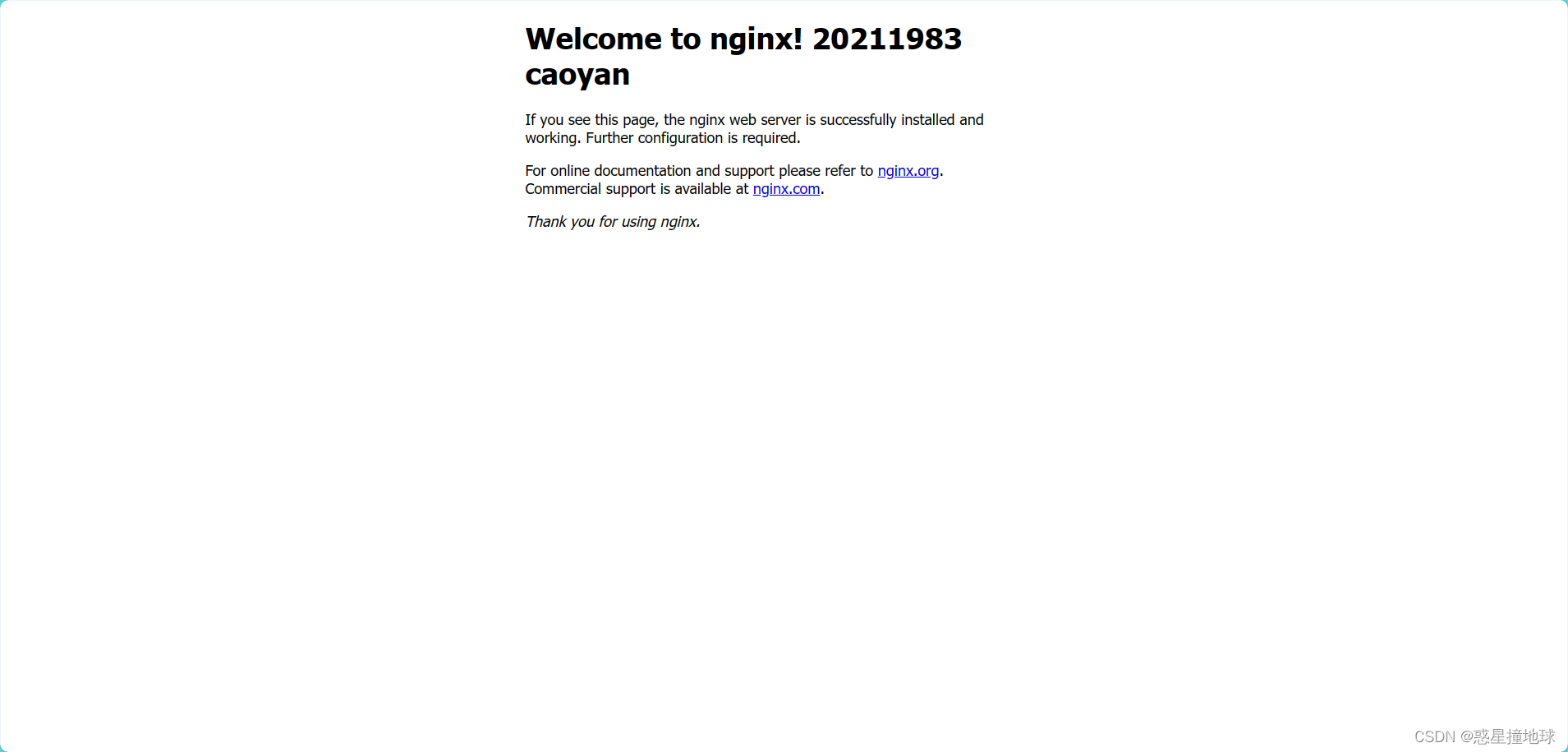
大数据与云计算实验一
检查是否开启 sudo service docker status 开启服务 sudo service docker start 运行服务 sudo docker run -itd -p 8080:80 nginx 查询ID docker ps -all 进入容器shell sudo docker exec -it <容器ID或容器名称> /bin/bash 找到/usr/share/nginx/html/index.…...
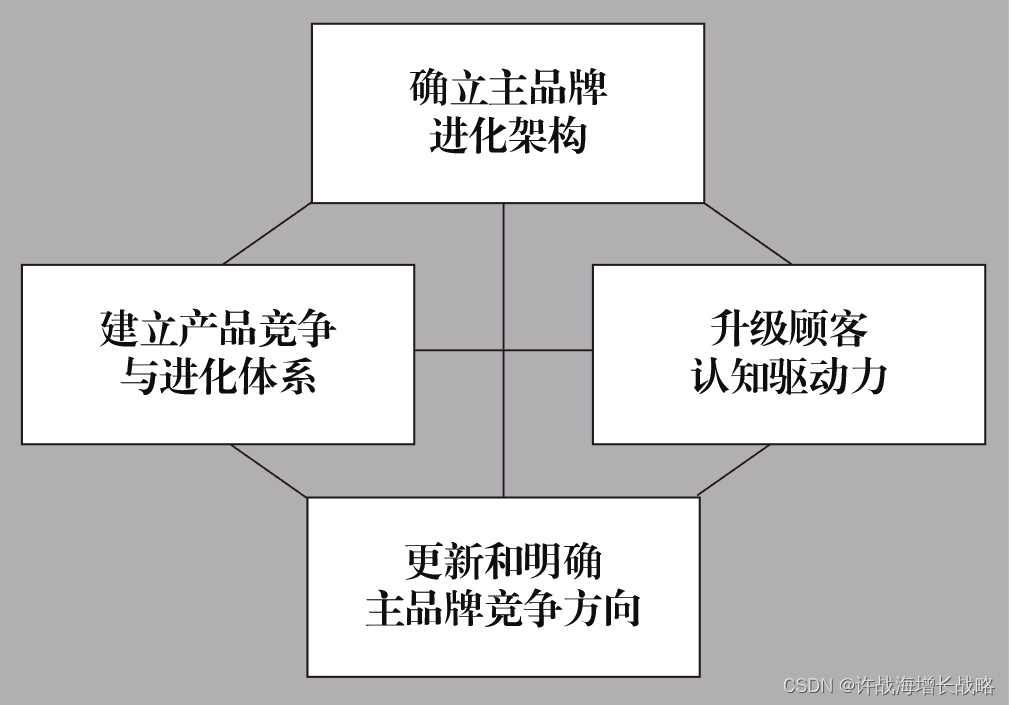
实施主品牌进化战略(一):确立主品牌进化架构
主品牌进化战略,即以主品牌为核心创造、巩固、转化竞争优势应对竞争环境变化,避免衰退,回归增长,让主品牌进化的方法论体系。主品牌进化战略制定要从 4 个方面出发:确立主品牌进化架构、更新和明确主品牌竞争方向、建立…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
