通俗神经网络
经典的全连接神经网络
经典的全连接神经网络来包含四层网络:输入层、两个隐含层和输出层,将手写数字识别任务通过全连接神经网络表示,如 图3 所示。
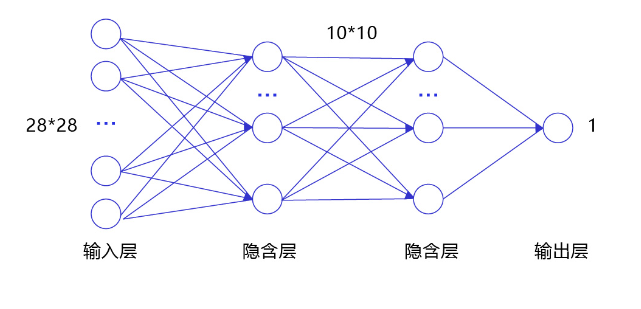
图3:手写数字识别任务的全连接神经网络结构
- 输入层:将数据输入给神经网络。在该任务中,输入层的尺度为28×28的像素值。
- 隐含层:增加网络深度和复杂度,隐含层的节点数是可以调整的,节点数越多,神经网络表示能力越强,参数量也会增加。在该任务中,中间的两个隐含层为10×10的结构,通常隐含层会比输入层的尺寸小,以便对关键信息做抽象,激活函数使用常见的Sigmoid函数。
- 输出层:输出网络计算结果,输出层的节点数是固定的。如果是回归问题,节点数量为需要回归的数字数量。如果是分类问题,则是分类标签的数量。在该任务中,模型的输出是回归一个数字,输出层的尺寸为1。
说明:
隐含层引入非线性激活函数Sigmoid是为了增加神经网络的非线性能力。
举例来说,如果一个神经网络采用线性变换,有四个输入x1x_1x1~x4x_4x4,一个输出yyy。假设第一层的变换是z1=x1−x2z_1=x_1-x_2z1=x1−x2和z2=x3+x4z_2=x_3+x_4z2=x3+x4,第二层的变换是y=z1+z2y=z_1+z_2y=z1+z2,则将两层的变换展开后得到y=x1−x2+x3+x4y=x_1-x_2+x_3+x_4y=x1−x2+x3+x4。也就是说,无论中间累积了多少层线性变换,原始输入和最终输出之间依然是线性关系。
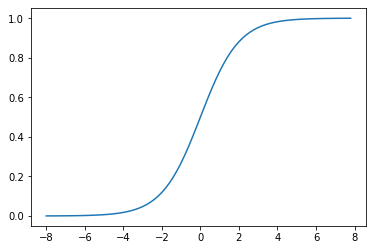
Sigmoid是早期神经网络模型中常见的非线性变换函数,绘制出Sigmoid的函数曲线。
卷积神经网络
虽然使用经典的全连接神经网络可以提升一定的准确率,但其输入数据的形式导致丢失了图像像素间的空间信息,这影响了网络对图像内容的理解。对于计算机视觉问题,效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化,可以直接处理原始形式的图像数据,保留像素间的空间信息,因此更适合处理视觉问题。
卷积神经网络由多个卷积层和池化层组成,如 图4 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示,池化层对这些特征表示进行过滤,保留最关键的特征信息。
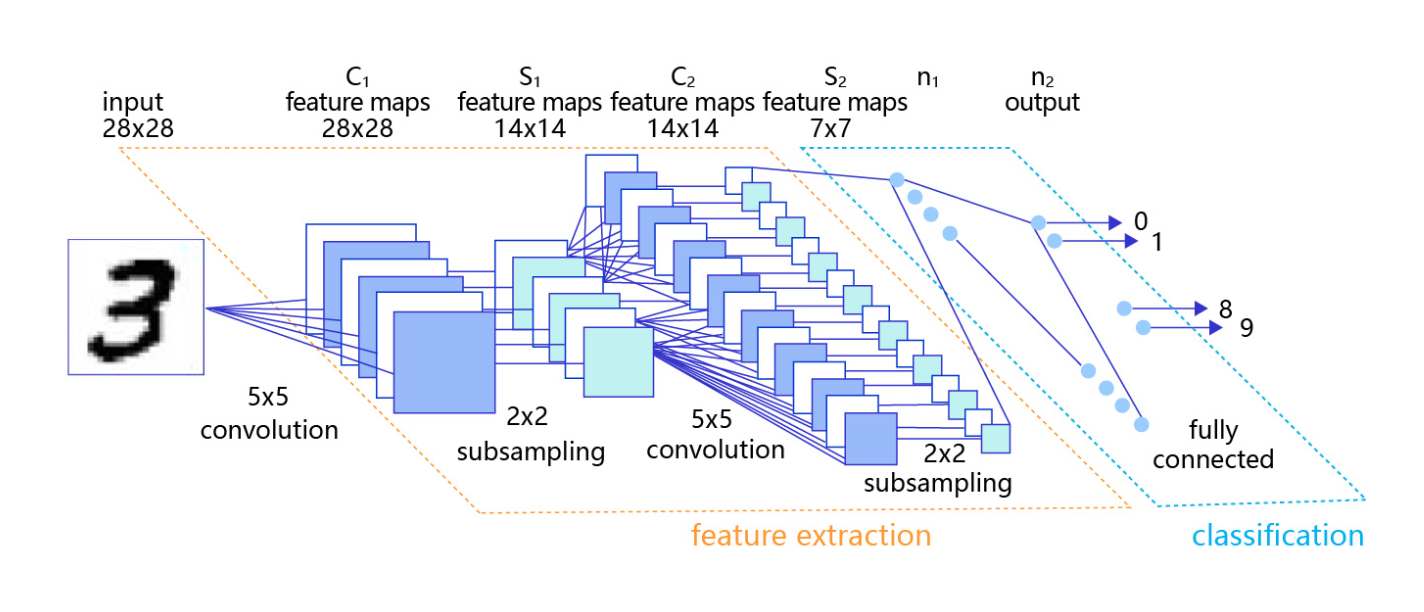
图4:在处理计算机视觉任务中大放异彩的卷积神经网络
说明:
本节只简单介绍用卷积神经网络实现手写数字识别任务,以及它带来的效果提升。读者可以将卷积神经网络先简单的理解成是一种比经典的全连接神经网络更强大的模型即可,更详细的原理和实现在接下来的《计算机视觉-卷积神经网络基础》中讲述。
两层卷积和池化的神经网络实现如下所示。
# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)# 定义一层全连接层,输出维度是1self.fc = Linear(in_features=980, out_features=1)# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出# 卷积层激活函数使用Relu,全连接层不使用激活函数def forward(self, inputs):x = self.conv1(inputs)x = F.relu(x)x = self.max_pool1(x)x = self.conv2(x)x = F.relu(x)x = self.max_pool2(x)x = paddle.reshape(x, [x.shape[0], -1])x = self.fc(x)return x
使用MNIST数据集训练定义好的卷积神经网络,如下所示。
说明:
以上数据加载函数load_data返回一个数据迭代器train_loader,该train_loader在每次迭代时的数据shape为[batch_size, 784],因此需要将该数据形式reshape为图像数据形式[batch_size, 1, 28, 28],其中第二维代表图像的通道数(在MNIST数据集中每张图片的通道数为1,传统RGB图片通道数为3)。
#网络结构部分之后的代码,保持不变
def train(model):model.train()#调用加载数据的函数,获得MNIST训练数据集train_loader = load_data('train')# 使用SGD优化器,learning_rate设置为0.01opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())# 训练5轮EPOCH_NUM = 10# MNIST图像高和宽IMG_ROWS, IMG_COLS = 28, 28loss_list = []for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失,取一个批次样本损失的平均值loss = F.square_error_cost(predicts, labels)avg_loss = paddle.mean(loss)#每训练200批次的数据,打印下当前Loss的情况if batch_id % 200 == 0:loss = avg_loss.numpy()[0]loss_list.append(loss)print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, loss))#后向传播,更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()#保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')return loss_listmodel = MNIST()
loss_list = train(model)
相关文章:

通俗神经网络
经典的全连接神经网络 经典的全连接神经网络来包含四层网络:输入层、两个隐含层和输出层,将手写数字识别任务通过全连接神经网络表示,如 图3 所示。 图3:手写数字识别任务的全连接神经网络结构输入层:将数据输入给神经…...
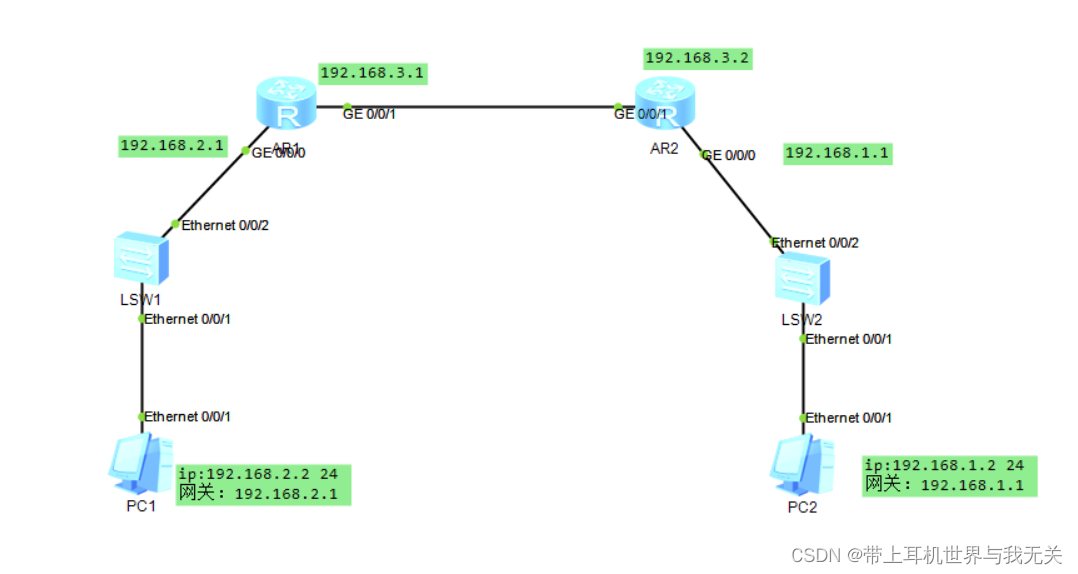
网络工程(一) 简单的配置
网络工程 简单的配置 需求 两台交换机 两台路由器 两台PC AR1配置静态路由 system-view [HUAWEI]sysname ar1 [ar1]interface g 0/0/0 [ar1-G…0/0/0]ip address 192.168.2.1 24 [ar1-G…0/0/0]quit [ar1]interface g 0/0/1 [ar1-G…0/0/1]ip address 192.168.3.1 24 [ar1-G…...

深度剖析数据在内存中的存储(上)
目录 1. 数据类型介绍 1.1 类型的基本归类 2. 整形在内存中的存储 2.1 原码、反码、补码 2.2 大小端介绍 2.3 一道小题 本章重点 1. 数据类型详细介绍 2. 整形在内存中的存储:原码、反码、补码 3. 大小端字节序介绍及判断 4. 浮点型在内存中的存储解析 正文…...

CF Edu 130 A-D vp 补题
CF Edu 130 A-D vp 补题 数模也是终于结束了。开始恢复vp。今天这场vp发挥比上次好一些,三题rank3600。A,B题做的很顺利。C题标记没弄全多WA了两发。D题是个交互题,也是研究了一下。基本思路正确。 题目链接 A. Parkway Walk 贪心 题意&am…...

4707: 统计数字个数
描述给定一个非负整数a,求其中含有数字b的个数(0<a<2147483647,0<b<9)。如100001中含所有0的个数为4,1的个数为2。输入输入数据有多组,每组一行,每行为两个整数,即a和b&…...
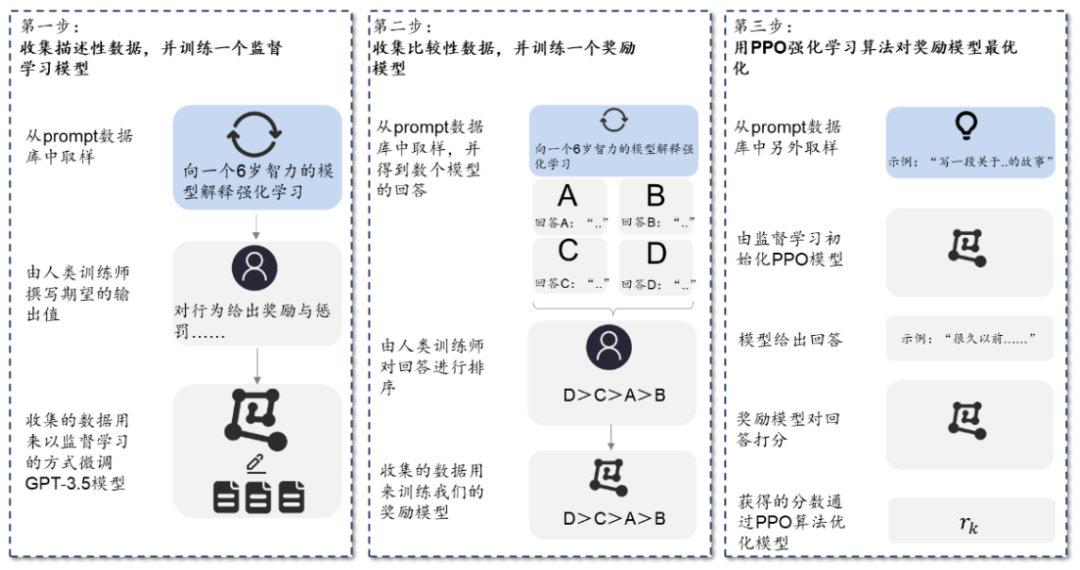
ChatGPT 编写模式:如何高效地将思维框架赋予 AI ?
如何理解 Prompt ?Prompt Enginneeringprompt 通常指的是一个输入的文本段落或短语,作为生成模型输出的起点或引导。prompt 可以是一个问题、一段文字描述、一段对话或任何形式的文本输入,模型会基于 prompt 所提供的上下文和语义信息&#x…...
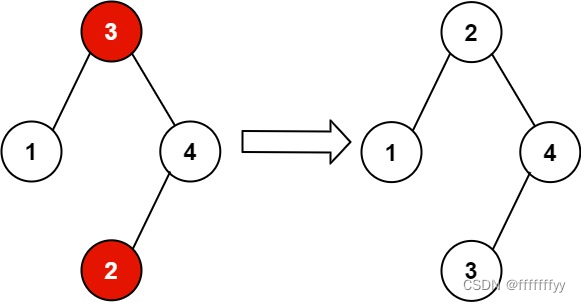
Leetcode力扣秋招刷题路-0099
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 99. 恢复二叉搜索树 给你二叉搜索树的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。 示例 1: 输入…...
消费升级趋势下,平台如何在广告电商模式中攫取新流量
如今电商平台飞速发展,越来越多的人加入电商运营的行列,同行竞争逐渐变得激烈起来,为了能够让平台有更多的展现机会,提升平台的商品转化率,大家都很重视平台的优化,因为一个好的平台可以给自身带来更多的流…...

华为OD机试真题 用 C++ 实现 - 众数和中位数 | 多看题,提高通过率
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
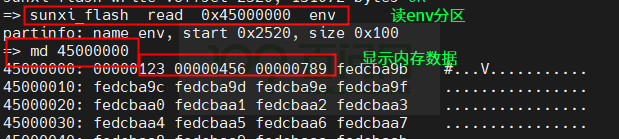
Linux NOR 开发指南
Linux NOR 开发指南 1 简介 编写目的 此文档描述Sunxi NOR 模块的使用方法,为相关人员调试提供指导 适用范围 boot0: 适用于brandy-2.0u-boot: 适用于u-boot-2018kernel: 适用于linux-4.9/linux-5.4 内核 BSP 的开发人员、测试人员 2 模块介绍 2.1 模块功能…...

免费领取丨精算与金融建模行业解决方案白皮书,不要错过!
一、我国精算行业现状 精算学是对人类社会所面临的各种风险及其他客观事务进行量化分析和处理的一门科学。在保险、金融、投资和各类风险管理等许多领域得到广泛应用,尤其在保险和社会保障领域,已成为不可或缺的科学和技术,以保险公司为例&a…...

ideal创建maven项目
前置工作本机安装mavenIdea 设置使用本机maven 工具Settings--->Maven开始创建maven项目创建maven项目,勾选通过模板创建,选择 maven-archetype-webapp 模板GroupId: 公司名倒序ArtifactId: 项目名设置本地maven仓库配置项目文件显示名,和…...
ChatGPT是什么?为何会引爆国内算力需求?
过去十年中,通过“深度学习大算力”从而获得训练模型是实现人工智能的主流技术途径。由于深度学习、数据和算力这三个要素都已具备,全世界掀起了“大炼模型”的热潮,也催生了大批人工智能企业。大模型是人工智能的发展趋势和未来大模型&#…...

【Linux】进程间通信(万字详解)—— 匿名管道 | 命名管道 | System V | 共享内存
🌈欢迎来到Linux专栏~~进程通信 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤…...
【Database-02】达梦数据库 - DM Manager管理工具安装
1、简介 DM Manager是达梦数据库自带的图形化界面管理工具,在安装达梦数据库的时候就会自动安装。 Linux环境,默认安装路径为:达梦安装目录/tool/manager,如果Linux是安装GUI,那么就可以直接启动使用。 实际大部分使…...
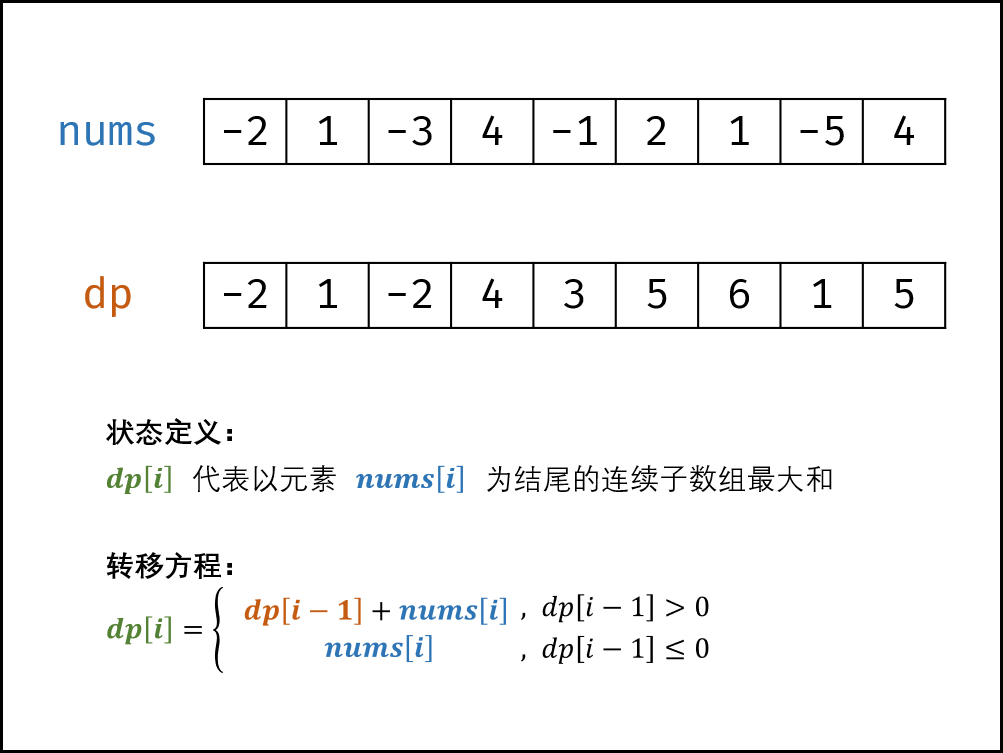
剑指 Offer 42. 连续子数组的最大和
剑指 Offer 42. 连续子数组的最大和 难度:easy\color{Green}{easy}easy 题目描述 输入一个整型数组,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。 要求时间复杂度为O(n)。 示例1: 输入: nums [-2,1,-3,4,-1,2,1,-5,4] 输…...

双指针 (C/C++)
1. 双指针 双指针算法的核心思想:将暴力解法的时间复杂度,通常是O(N*N),通过某种特殊的性质优化到O(N)。 做题思路:先想想暴力解法的思路,然后分析这道题的特殊性质,一般是单调性。然后得出双指针算法的思路…...
CVE-2023-23752 Joomla未授权访问漏洞分析
漏洞概要 Joomla 在海外使用较多,是一套使用 PHP 和 MySQL 开发的开源、跨平台的内容管理系统(CMS)。 Joomla 4.0.0 至 4.2.7 版本中的 ApiRouter.php#parseApiRoute 在处理用户的 Get 请求时未对请求参数有效过滤,导致攻击者可向 Joomla 服务端点发送包…...
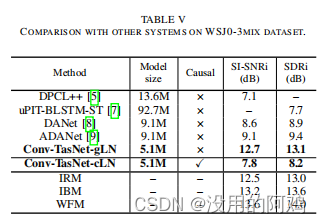
单通道说话人语音分离——Conv-TasNet(Convolutional Time-domain audio separation Network)
单通道说话人语音分离——Conv-TasNet模型(Convolutional Time-domain audio separation Network) 参考文献:《Conv-TasNet: Surpassing Ideal Time-FrequencyMagnitude Masking for Speech Separation》 1.背景 在真实的声学环境中,鲁棒的语音处理通常…...
)
华为OD机试真题Python实现【环中最长子串】真题+解题思路+代码(20222023)
环中最长子串 题目 给你一个字符串s,首尾相连成一个环形, 请你在环中找出o字符出现了偶数次最长子字符串的长度. 备注: 1 <= s.lenth <= 5x10^5 s只包含小写英文字母 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Python)真题目录汇总 ## 输入 输入是…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
