Day69:283. 移动零、11. 盛最多水的容器、42. 接雨水
283. 移动零
leetcode链接:https://leetcode.cn/problems/move-zeroes/
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作。示例 1:输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:输入: nums = [0]
输出: [0]
提示:1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1
进阶:你能尽量减少完成的操作次数吗?
这题就是一个典型的快慢指针问题,类似于从数组中删除指定元素。快指针依次遍历,慢指针用来存放元素。思路就是先把所有的0元素删除,再在数组末位填充0,代码如下:
class Solution {
public:void moveZeroes(vector<int>& nums) {int slow = 0;for(int i = 0 ; i < nums.size(); i++){if(nums[i] != 0){nums[slow++] =nums[i];}}//把剩下的位置填充为0for(int i = slow; i < nums.size(); i++){nums[i] = 0;}}
};
11.盛最多水的容器
给定一个长度为 n 的整数数组 height 。
有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明:你不能倾斜容器。
这题是贪心算法,
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。示例 1:输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:输入:height = [4,2,0,3,2,5]
输出:9
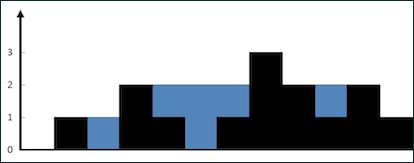
对于这种问题,我们不要想整体,而应该去想局部。仅仅对于位置 i,能装下多少水呢?
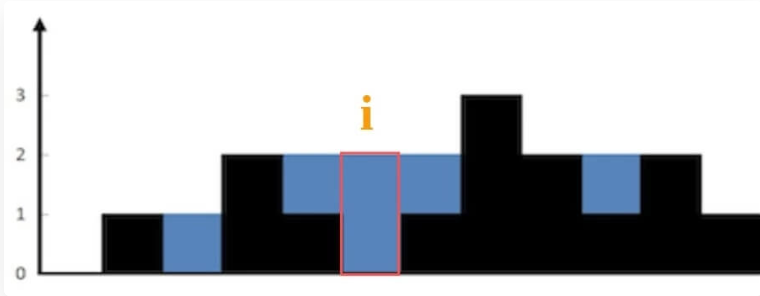
能装 2 格水,因为 height[i] 的高度为 0,而这里最多能盛 2 格水,2-0=2。
为什么位置 i 最多能盛 2 格水呢?因为,位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关,我们分别称这两个柱子高度为 l_max 和 r_max;位置 i 最大的水柱高度就是 min(l_max, r_max)。
也就是说:
water[i] = min(# 左边最高的柱子max(height[0..i]), # 右边最高的柱子max(height[i..end]) ) - height[i]
根据该思路写一个暴力解法。
暴力解法
class Solution {
public:int trap(vector<int>& height) {int res = 0;for(int i = 1; i < height.size() - 1; i++){//这样才能保证左右都有柱子int leftMax= 0, rightMax = 0;for (int j = i; j < height.size(); j++)rightMax = max(rightMax, height[j]);// 找左边最高的柱子for (int j = i; j >= 0; j--)leftMax = max(leftMax, height[j]);cout<< leftMax << ',' << rightMax << endl;res += max(0, min(leftMax,rightMax) - height[i]);}return res;}
};
时间复杂度O(n2),实际上不需要每次都遍历,可以借助备忘录。
这里实际上res加的时候时候不需要和0比较,因为在计算 l_max 数组的时候是取「自己高度」和「目前左边最高」的最大值,因此 l_max[i] >= height[i] 是恒成立的。r_max 同理。
备忘录
不用每次都计算left和right,计算一次就好,存储在两个数组中:
class Solution {
public:int trap(vector<int>& height) {if (height.size() == 0) {return 0;}int res = 0;vector<int> leftMax(height.size(), 0);vector<int> rightMax(height.size(), 0);leftMax[0] = height[0];rightMax[height.size() - 1] = height[height.size() - 1];for(int i = 1; i < height.size() - 1; i++){//这样才能保证左右都有柱子leftMax[i] = max(height[i], leftMax[i - 1]);}for(int i = height.size() - 2; i >= 0; i--){rightMax[i] = max(height[i], rightMax[i + 1]);}for(int i = 1; i < height.size() - 1; i++){res += min(leftMax[i],rightMax[i]) - height[i];}return res;}
};
把时间复杂度降低为 O(N),已经是最优了,但是空间复杂度是 O(N)。双指针法可以把空间复杂度降到O(1)。
双指针法
之前不管是暴力解法还是备忘录,leftMax和rightMax分别代表 height[0..i] 和 height[i..end] 的最高柱子高度:
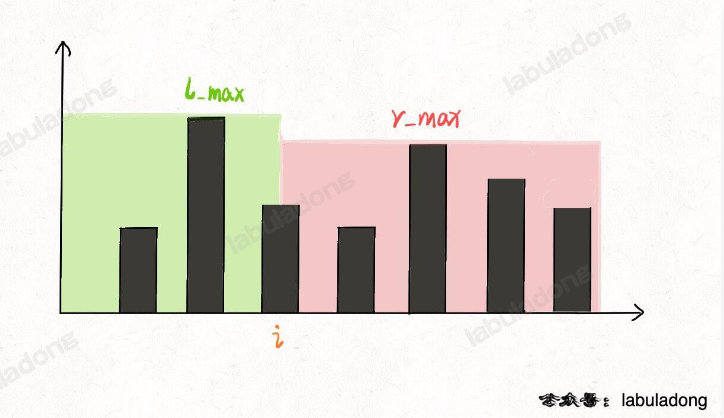
而在双指针法中,代表的是 height[0..left] 和 height[right..end] 的最高柱子高度:
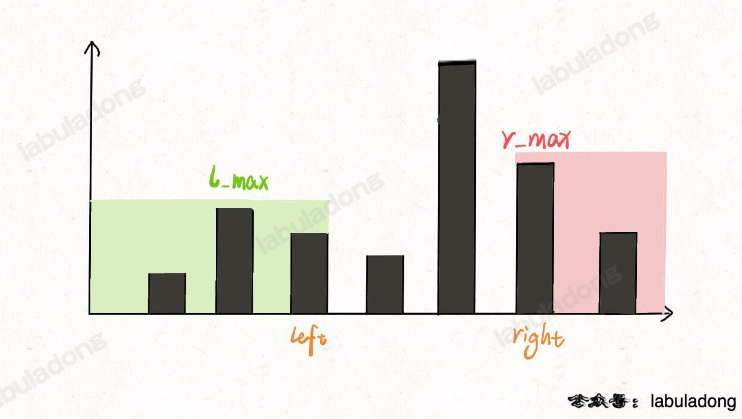
我们只在乎 min(l_max, r_max)。对于上图的情况,我们已经知道 l_max < r_max 了,至于这个 r_max 是不是右边最大的,不重要。重要的是 height[i] 能够装的水只和较低的 l_max 之差有关。
最终代码:
class Solution {
public:int trap(vector<int>& height) {int left = 0, right = height.size() - 1;int leftMax = 0, rightMax = 0;int res = 0;while (left < right) {leftMax = max(leftMax, height[left]);rightMax = max(rightMax, height[right]);// res += min(leftMax, rightMax) - height[i]if (leftMax < rightMax) {res += leftMax - height[left];left++;} else {res += rightMax - height[right];right--;}}return res;}
};
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,
第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明:你不能倾斜容器。
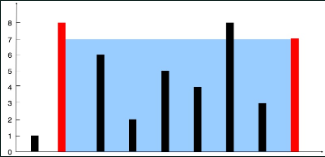
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
跟上面的题类似,直接贴代码:
class Solution {
public:int maxArea(vector<int>& height) {int res = 0;int left = 0, right = height.size() - 1;while(left < right){res = max(res, min(height[left], height[right]) * (right - left));if(height[left] < height[right]){left++;}else{right--;}}return res;}
};
这里要注意双指针的移动顺序,为什么是往height[i]小的那边移动?因为矩形的最大面积是由最短的那条边决定的:如果移动较低的那一边,那条边可能会变高,使得矩形的高度变大,进而就「有可能」使得矩形的面积变大;相反,如果你去移动较高的那一边,矩形的高度是无论如何都不会变大的,所以不可能使矩形的面积变得更大。
总结
感觉这样复习还是太零散没有体系了,从明天开始,还是按照模块来,先把原来的题二刷掉,然后再找拓展题。
相关文章:

Day69:283. 移动零、11. 盛最多水的容器、42. 接雨水
283. 移动零 leetcode链接:https://leetcode.cn/problems/move-zeroes/ 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作。示例 1:…...

tensorrt的安装和使用
安装 提前安装好 CUDA 和 CUDNN,登录 NVIDIA 官方网站下载和主机 CUDA 版本适配的 TensorRT 压缩包即可。 以 CUDA 版本是 10.2 为例,选择适配 CUDA 10.2 的 tar 包,然后执行类似如下的命令安装并测试: #安装c版本 cd /the/pat…...

电压放大器在电子测试中的应用有哪些方面
电压放大器是一种常见的电子设备,广泛应用于各种测试和测量应用中。以下是电压放大器在电子测试中的几个主要方面应用的简要介绍。 信号采集与处理:电压放大器通常用于信号采集和处理,在测试过程中将低电平信号放大到适合进一步处理或分析的水…...

39.地址算术运算
如果p是一个指向数组中某个元素的指针,那么p将会对p进行自增运算并指向下一个元素,而pi将对p进行加i的增量运算,使其指向指针p当前所指向的元素之后的第i个元素。这类运算时指针或地址算术运算中最简单的形式。 allocbuf中的空间使用状况也是…...

没有外网的麒麟系统上搭建GitLab服务并且无需客户端账号密码验证
要在没有外网的麒麟系统上搭建GitLab服务并且无需客户端账号密码验证,可以按照以下步骤进行操作: 安装必要的依赖包和软件 sudo yum install curl policycoreutils-python openssh-server openssh-clients sudo systemctl enable sshd sudo systemctl …...

微服务生态系统:使用Spring Cloud构建分布式系统
文章目录 什么是微服务?为什么选择Spring Cloud?Spring Cloud的关键组件示例:构建一个简单的微服务步骤1:创建Spring Boot项目步骤2:配置Eureka服务发现步骤3:创建REST控制器步骤4:运行项目步骤…...
DIY 一个汽车方向盘游戏外设(MMOS OSW DIY)
OSW-MMOS直驱方向盘DIY过程记录 - 简书 (jianshu.com) DIY 一个汽车方向盘游戏外设(MMOS OSW DIY) 首先讲一下这个直驱系统大概的框架,首先是电脑,电脑里装MMOS的软件(这个软件国内高手把它汉化了的),电脑通过USB线&a…...

校园网络技术需求分析
路由技术: 路由协议工作在 OSI 参考模型的第 3 层,因此它的作用主要是在通信 子网间路由数据包。路由器具有在网络中传递数据时选择最佳路径的能力。 除了可以完成主要的路由任务,利用访问控制列表(Access Control List&#x…...
计算机网络(二):TCP篇
文章目录 1. TCP头部包含哪些内容?2. 为什么需要 TCP 协议? TCP 工作在哪一层?3. 什么是 TCP ?4. 什么是 TCP 连接?5. 如何唯一确定一个 TCP 连接呢?6. UDP头部大小是多少?包含哪些内容…...

测试登录界面:Python
import unittest from selenium import webdriver class LoginTest(unittest.TestCase): def setUp(self): self.driver webdriver.Chrome() def test_login(self): # 打开登录页面 self.driver.get("http://example.com/login") # 输入用户名和密码 user…...

Rust踩雷笔记(7)——两个链表题例子初识裸指针
目录 leetcode 234leetcode 19 leetcode 234 题目在这https://leetcode.cn/problems/palindrome-linked-list/,leetcode 234的回文链表,思路很简单,就是fast和slow两个指针,fast一次移动两个、slow一次一个,最后slow指…...

用什么命令看Linux系统的体系架构
要查看Linux系统的体系架构,可以使用uname命令。在终端中运行以下命令: uname -m该命令将返回系统的体系架构,例如x86_64表示64位系统,i686表示32位系统。 uname 使用方法 uname命令用于获取操作系统的相关信息。它可以用于显示…...

消息中间件大揭秘:选择之前你必须知道的关键信息
Hello大家好!我是小米,很高兴再次和大家见面!今天的话题非常精彩,我们将深入探讨消息中间件,并了解一些常见的消息队列:RabbitMQ、RocketMQ、Kafka以及Redis。如果你正在准备面试,或者只是对这些…...

【Unity基础】4.动画Animation
【Unity基础】4.动画Animation 大家好,我是Lampard~~ 欢迎来到Unity基础系列博客,所学知识来自B站阿发老师~感谢 (一)Unity动画编辑器 (1)Animation组件 这一张我们要学习如何在unity编辑器中&…...
FreeRTOS移植以及核心功能
文章目录 freertos和ucos区别,优缺点比较移植步骤核心功能内存管理(5种内存管理策略)FreeRTOS任务调度算法有三种时间管理通信管理 栈管理 freertos和ucos区别,优缺点比较 FreeRTOS(Free Real-Time Operating System&…...
重装系统(配置环境)
这里写目录标题 0.重装系统1.python1.1 anaconda1.2 pycharm1.3 深度学习环境配置 2.java2.1.安装JDK2.2.配置JDK环境变量2.3IDEA2.4 Maven 3.大数据3.1 虚拟机3.2 Hadoop平台3.3 存储3.4 采集3.5 计算3.6 查询3.7 可视化 0.重装系统 // An highlighted block var foo bar;1.…...

docker系列-报错以及解决指南
1. windows运行docker报错Windows Hypervisor is not presentDocker Desktop is unable to detect a Hypervisor.Hardware assisted virtualization and data execution protection must be enabled in the BIOS. Docker Desktop - Windows Hypervisor is not presentDocker D…...

Vue3快速上手
1.Vue3简介 2020年9月18日,Vue.js发布3.0版本,代号:One Piece(海贼王)耗时2年多、2600次提交、30个RFC、600次PR、99位贡献者github上的tags地址:Release v3.0.0 One Piece vuejs/core GitHub 2.Vue3带…...
二叉搜索树(BST,Binary Search Tree)
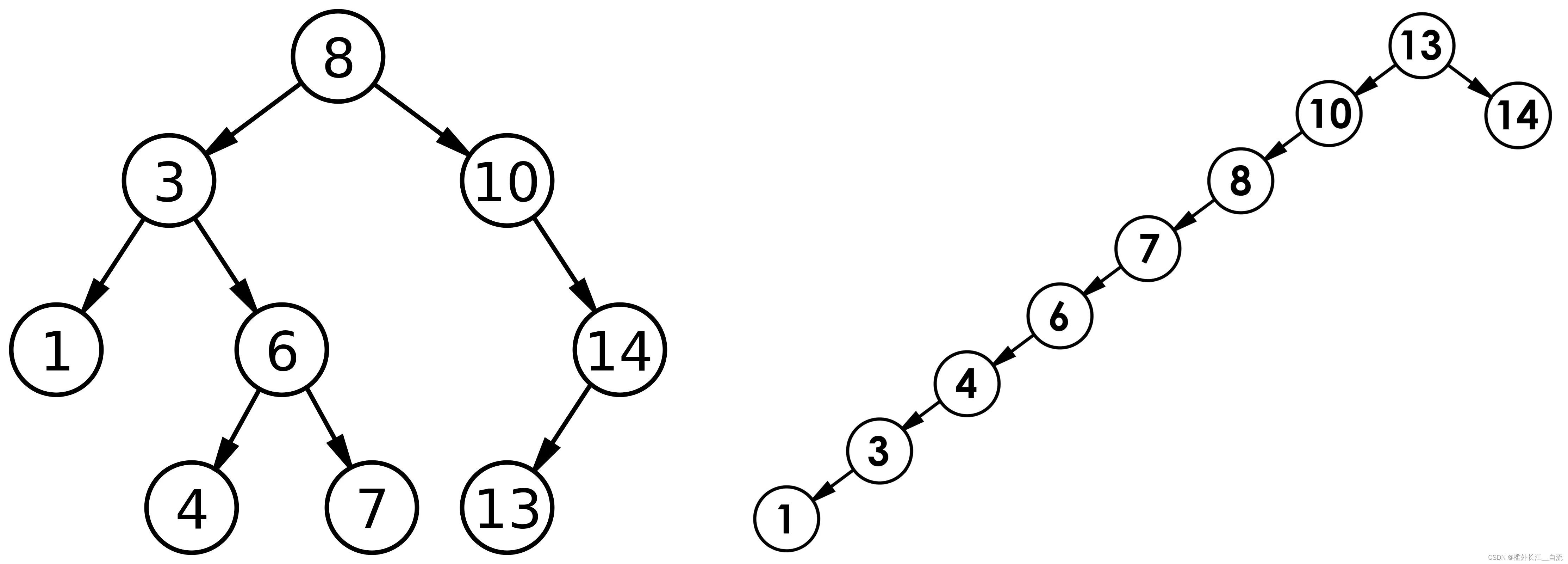
文章目录 1. 二叉搜索树1.1 二叉搜索树概念1.2 二叉搜索树的查找1.3 二叉搜索树的插入1.4 二叉搜索树的删除 2 二叉搜索树的实现3 二叉搜索树的应用3.1二叉搜索树的性能分析 1. 二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树…...
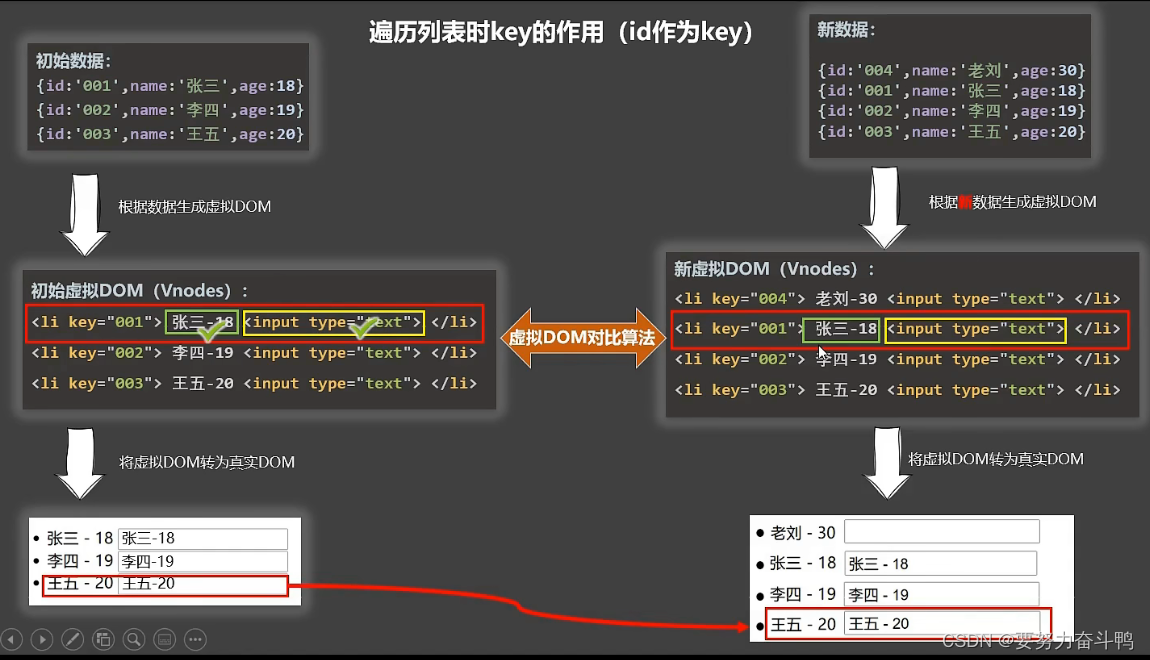
分析key原理
总结: key是虚拟dom对象的标识,当数据发生变化时,vue会根据新数据生成新的虚拟dom,随后vue进行新虚拟dom与旧虚拟dom的差异比较 比较规则: ①旧虚拟dom中找到了与新虚拟dom相同的key 若虚拟dom中的内容没变,…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
