掌握这些算法,让你的编程之路更顺畅——重要算法解析
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。这些算法通常被广泛应用于日常编程工作中,是提升编程效率和解决实际问题的重要工具。本文将介绍几种十分重要的“必抓!”算法,希望能对广大程序员朋友们提供一些帮助。
程序员的必抓算法:
一:引言
在编程的世界里,算法是解决问题的核心。一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。这些算法通常被广泛应用于日常编程工作中,是提升编程效率和解决实际问题的重要工具。今天就来聊聊这些十分重要的“必抓!”算法吧~我们将按照引言、常见算法介绍和重点算法总结三点展开,帮助你全面了解这些关键算法。
二:常见算法介绍
- 二分查找算法
二分查找算法是一种非常经典的查找算法,适用于有序数组或列表中查找特定元素。它的主要思想是通过将目标值与数组或列表中间元素进行比较,不断缩小查找范围,直到找到目标值或确定目标值不存在于数组或列表中。二分查找算法在实现上具有较高的效率和灵活性,时间复杂度为O(log n),远优于线性查找算法。在实际编程工作中,二分查找算法被广泛应用于各种需要快速查找的场景,如数据压缩、加密解密等。
- 动态规划算法
动态规划算法是一种通过将问题分解为子问题,并存储子问题的解,以避免重复计算,从而提高效率的算法。它的主要思想是将问题分解为一系列相互依赖的子问题,通过求解子问题的最优解,得出原问题的最优解。动态规划算法在实现上具有较高的效率和可扩展性,适用于解决各种最优化问题,如背包问题、最长公共子序列等。在实际编程工作中,动态规划算法被广泛应用于各种需要优化解的场景,如机器学习、图像处理等。
三:重点算法总结
- 二分查找算法的重要性
在计算机科学和实际编程应用中,二分查找算法是一种非常重要的算法。它可以有效地在有序数组或列表中查找特定元素,比线性查找算法更加高效。它的应用场景非常广泛,包括但不限于数据压缩、加密解密等。掌握二分查找算法对于程序员来说非常重要,因为它可以提高查找效率,优化程序性能。
- 动态规划算法的重要性
动态规划算法是一种解决最优化问题的强大工具。它可以将一个复杂的问题分解为一系列简单的子问题,通过求解子问题的最优解得出原问题的最优解。在实际编程工作中,动态规划算法被广泛应用于各种需要优化解的场景,如机器学习、图像处理等。掌握动态规划算法对于程序员来说非常重要,因为它可以提高解决问题的效率,优化程序性能。
- 深度优先搜索和广度优先搜索的重要性
深度优先搜索和广度优先搜索是两种常用的图遍历算法。它们都可以用于遍历或搜索树或图结构中的节点。深度优先搜索是从根节点开始,沿着树的深度遍历树的节点,直到找到目标节点或遍历完所有节点。广度优先搜索也是从根节点开始,逐层遍历树的节点,直到找到目标节点或遍历完所有节点。它们的实际应用场景包括但不限于网络爬虫、路径规划、图片处理等。掌握深度优先搜索和广度优先搜索对于程序员来说非常重要,因为它们可以帮助我们高效地遍历或搜索图结构中的节点,优化程序性能。
结语
总结本文所介绍的几种十分重要的“必抓!”算法,我们可以发现它们在实现上都具有较高的效率和广泛应用价值。作为一个程序员,掌握这些算法是非常必要的,因为它们可以帮助我们更高效地解决实际问题,提升编程效率和代码质量。在掌握这些算法的过程中,我们需要注重理解算法的基本概念和思想,并根据实际应用场景进行灵活应用。此外,不断地练习和实践也是掌握这些算法的关键所在。希望本文能对广大程序员朋友们提供一些帮助,如有不当之处,还请指正。
相关文章:

掌握这些算法,让你的编程之路更顺畅——重要算法解析
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。这些算法通常被广泛应用于日常编程工作中,是提升编程效率和解决实际问题的重要工具。本文将介绍几种十分重要的“必抓…...
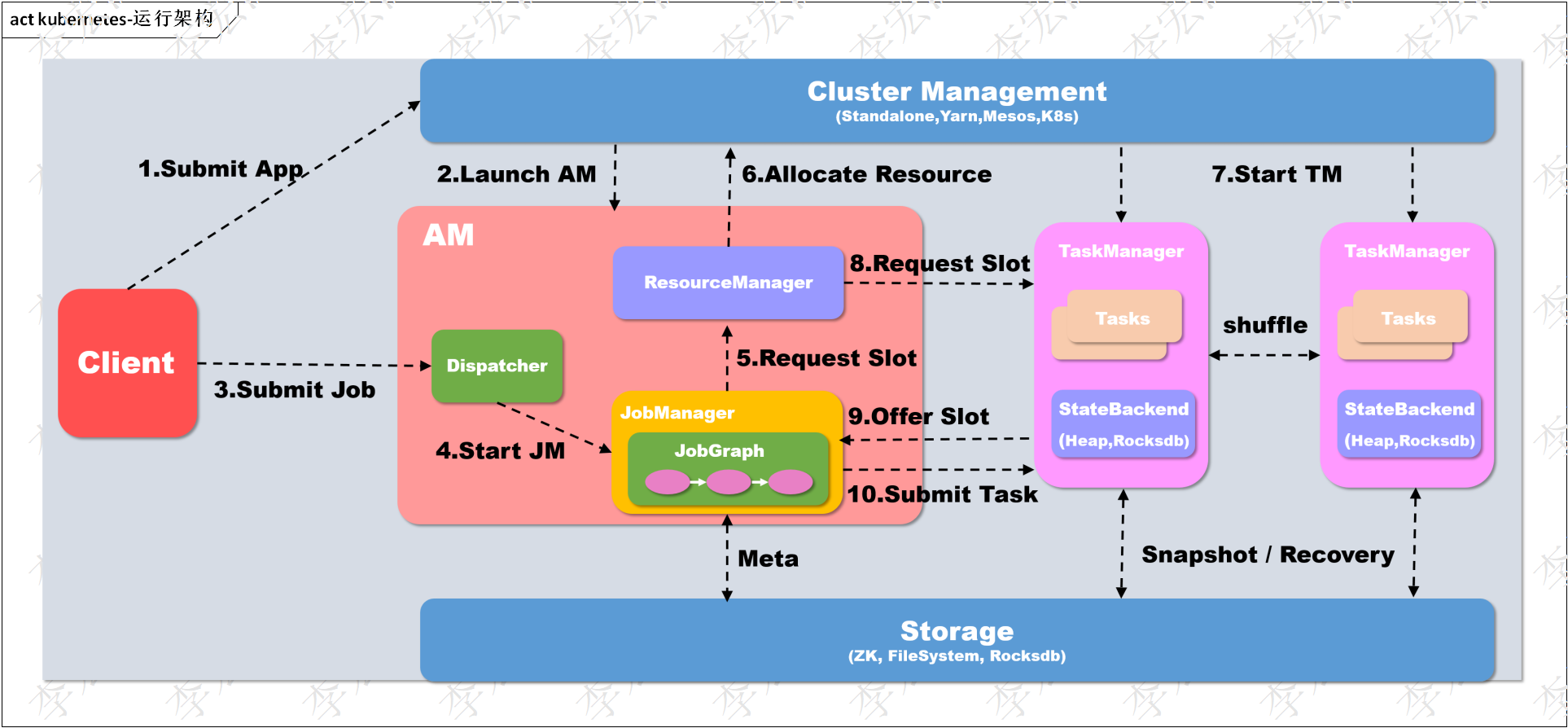
flink集群与资源@k8s源码分析-总述
1 简介 集群和资源模块提供动态资源能力,是分布式系统关键基础设施,分布式datax,分布式索引,事件引擎都需要集群和资源的弹性资源能力,提高伸缩性和作业处理能力。本文分析flink的集群和资源的k8s模块,深入了解其设计原理,为开发自有的集群和资源组件做技术准备, 同时涉…...

LeetCode 0213. 打家劫舍 II:动动态规划
【LetMeFly】213.打家劫舍 II:动动态规划 力扣题目链接:https://leetcode.cn/problems/house-robber-ii/ 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味…...
VMware17 不可恢复错误mks解决方案
用的虚拟机VMware17版本,然后运行带HDR的unity程序,结果报错 网上找了很多解决方案,都没用。毕竟需要在不放弃虚拟机3D加速的情况下运行。 最终皇天不负有心人,亲测有效的方法: 在虚拟机名字.vmx文件里添加以下2行&a…...
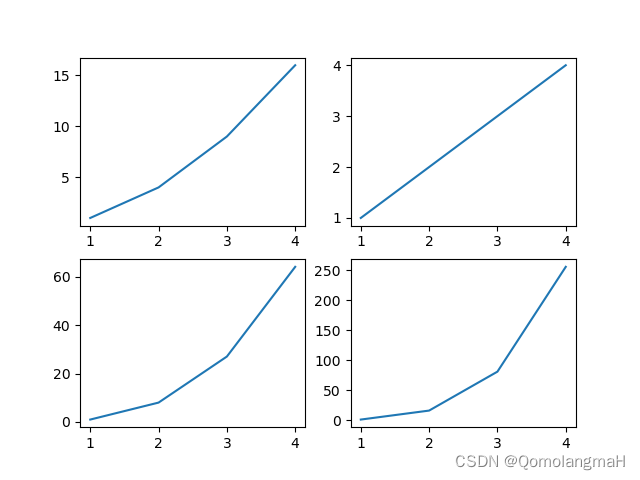
【深度学习】 Python 和 NumPy 系列教程(廿五):Matplotlib详解:3、多子图和布局:subplot()函数
目录 一、前言 二、实验环境 三、Matplotlib详解 1、2d绘图类型 2、3d绘图类型 3、多子图和布局 1. subplot()函数 简单示例 一、前言 Python是一种高级编程语言,由Guido van Rossum于1991年创建。它以简洁、易读的语法而闻名,并且具有强大的功能…...

计算机网络知识补充(1)
计算机网络:是一个将分散的,具有独立功能的计算机系统,通过通信设备和线路进行连接起来,由功能完善的软件实现资源共享和信息共享的系统,计算机网络是互连的,自治的计算机集合 互连:通过通信链路来进行互联互通 自治:没…...
C# Onnx Yolov8 Pose 姿态识别
效果 项目 代码 using Microsoft.ML.OnnxRuntime; using Microsoft.ML.OnnxRuntime.Tensors; using OpenCvSharp; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System…...

7.algorithm2e中while怎么使用
algorithm2e中while怎么使用 在 algorithm2e 宏包中,要使用 while 循环,您可以使用 \While 和 \EndWhile 命令来定义循环的开始和结束。以下是如何使用 while 循环的示例: \documentclass{article} \usepackage[linesnumbered,boxed]{algorit…...

Flask狼书笔记 | 08_个人博客(下)
文章目录 8 个人博客8.4 初始化博客8.5 使用Flask-Login管理用户认证8.6 CSRFProtect实现CSRF保护8.7 编写博客后台小结 8 个人博客 8.4 初始化博客 1、安全存储密码 密码不要以明文的形式直接存储在数据库中,以防被攻击者盗取、泄露。一般的做法是,不…...
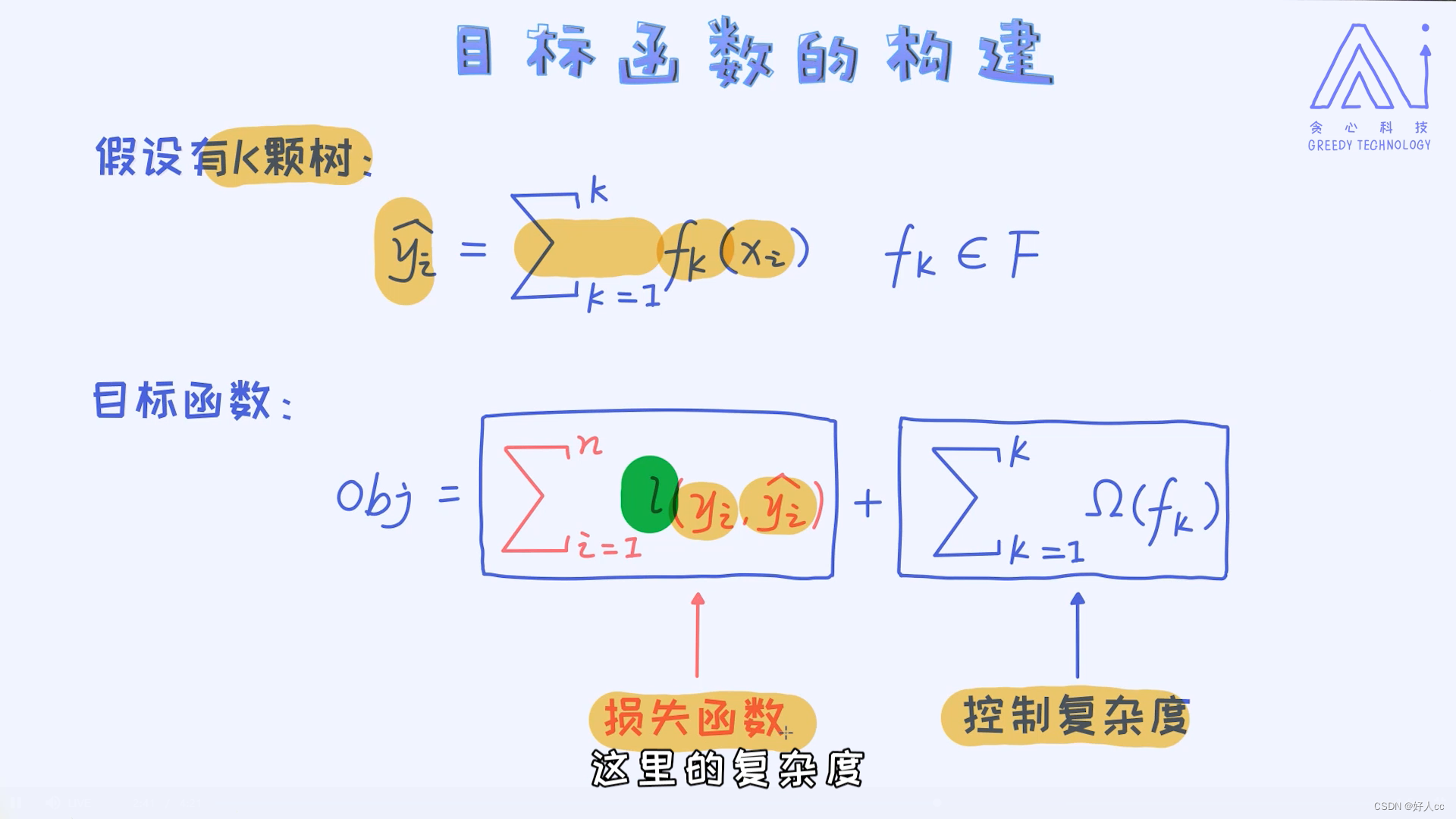
机器学习第十课--提升树
一.Bagging与Boosting的区别 在上一章里我们学习了一个集成模型叫作随机森林,而且也了解到随机森林属于Bagging的成员。本节我们重点来学习一下另外一种集成模型叫作Boosting。首先回顾一下什么叫Bagging? 比如在随机森林里,针对于样本数据,…...

react scss.modules中使用iconfont
全局引入详见全局引入scss 全局的scss文件中引入iconfont.css use "../font/iconfont.css"; 然后就可以正常使用啦...
使用Jmeter+ant进行接口自动化测试(数据驱动)
最近在做接口测试,因为公司有使用jmeter做接口测试的相关培训资料,所以还是先选择使用jmeter来批量管理接口,进行自动化测试。话不多说,进入正题: 1.使用csv文件保存接口测试用例,方便后期对接口进行维护&…...
可视化图表组件之股票数据分析应用
股市是市场经济的必然产物,在一个国家的金融领域之中有着举足轻重的地位。在过去,人们对于市场走势的把握主要依赖于经验和直觉,往往容易受到主观因素的影响,导致决策上出现偏差。如今,通过数据可视化呈现,…...
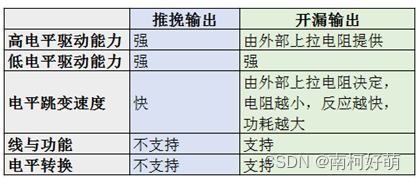
STM32 ~ GPIO不同模式之间的区别与实现原理
GPIO全称General Purpose Input Output ,即通用输入/输出。其实GPIO的本质就是芯片的一个引脚,通常在ARM中所有的I/O都是通用的。不过,由于每个开发板上都会设计不同的外围电路,这就造成了GPIO的功能可能有所不同。大部分GPIO都是…...
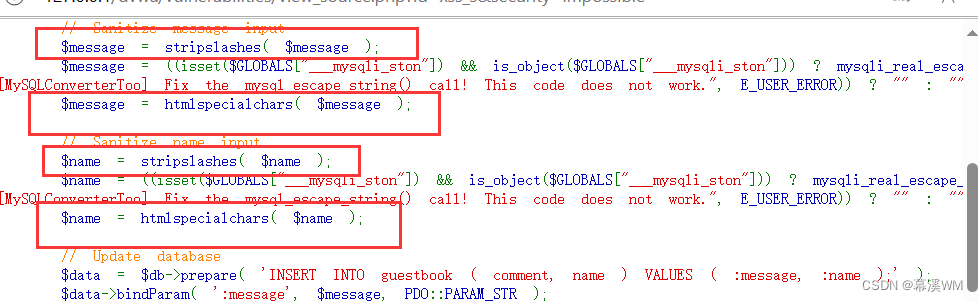
dvwa靶场通关(十二)
第十二关:Stored Cross Site Scripting (XSS)(存储型xss) low 这一关没有任何防护,直接输入弹窗代码 弹窗成功 medium 先试试上面的代码看看,有没有什么防护 发现我们的script标签不见了,应该是被过滤掉…...

【shell学习】企业运维工作中常用的shell脚本
本站以分享各种运维经验和运维所需要的技能为主 《python零基础入门》:python零基础入门学习 《python运维脚本》: python运维脚本实践 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8…...
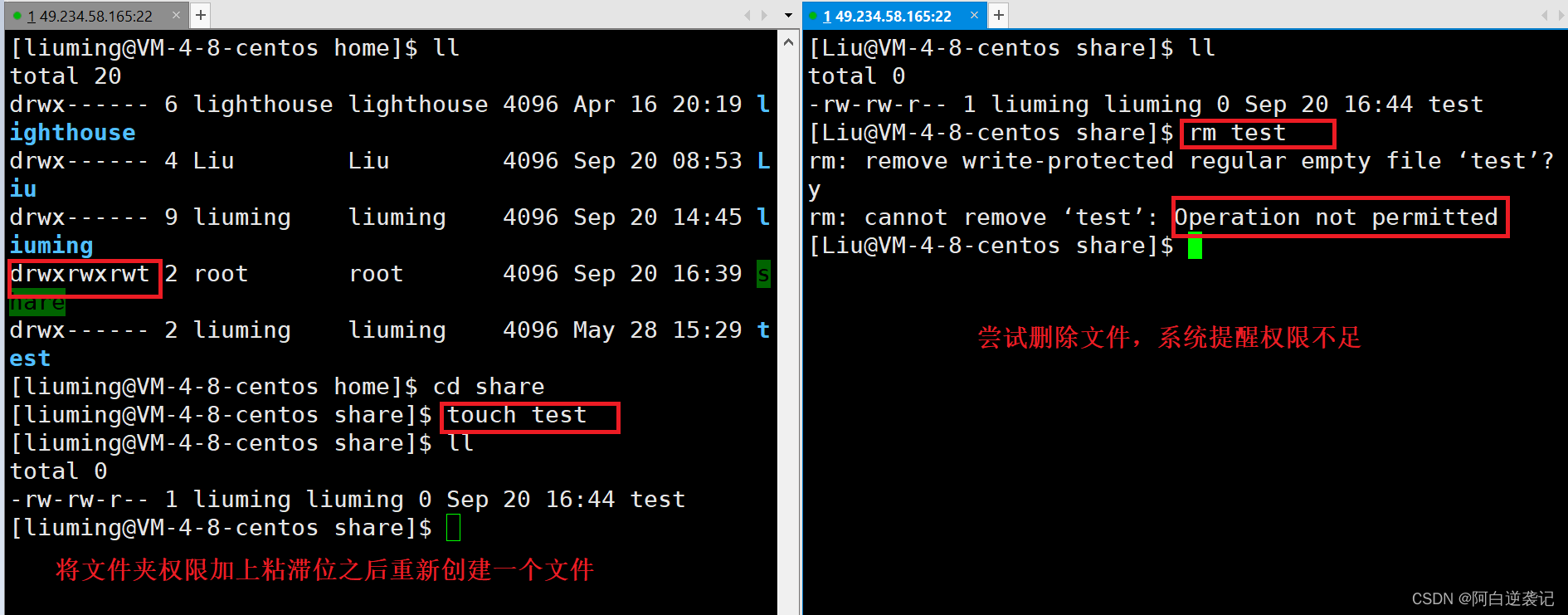
对权限的理解和使用
目录 一:用户权限: ★su命令 ★sudo命令 二:文件权限 ★文件的类型权限 ★文件夹的权限的使用 ▲文件夹的可读权限: ▲文件夹的可写权限: ▲文件夹的可执行权限: ★权限的修改操作 ▲chmod命令 ★对于文件的…...

MySQL 5.7 通过数据库idb文件快速导入至另一台数据库
前言 数据库有一张表里有1000万条数据,通过sql导入会非常缓慢,如果数据库版本相同,迁移表可以通过复制表idb文件实现快速迁移。 一、系统环境 原服务器系统:centos7.4 原服务器数据库版本:MySQL5.7.21 新服务器系统…...
第一章 计算机网络基础
目录 1.1 网络体系结构 1.1.1 OSI/RM七层参考模型 1.1.2 OSI/RM和TCP/IP模型的比较 1.1.3 五层协议的体系结构 1.1.4 计算机1向计算机2发送数据过程 1.1.5 TCP/IP体系结构的具体实现 1.2 网络设备概述 1.2.1 互联设备与OSI的对应关系 1.2.2 集线器(HUB) 1.2.3 网桥(B…...
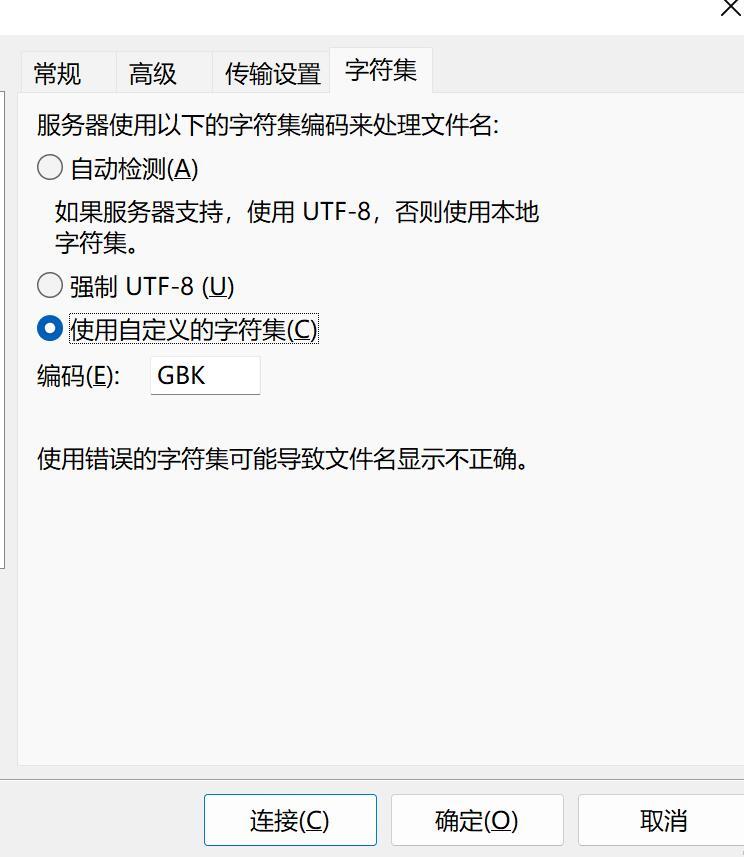
本地电脑搭建SFTP服务器,并实现公网访问
本地电脑搭建SFTP服务器,并实现公网访问 文章目录 本地电脑搭建SFTP服务器,并实现公网访问1. 搭建SFTP服务器1.1 下载 freesshd 服务器软件1.3 启动SFTP服务1.4 添加用户1.5 保存所有配置 2. 安装SFTP客户端FileZilla测试2.1 配置一个本地SFTP站点2.2 内…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
