机器学习入门教学——损失函数(交叉熵法)
1、前言
- 我们在训练神经网络时,最常用到的方法就是梯度下降法。在了解梯度下降法前,我们需要了解什么是损失(代价)函数。所谓求的梯度,就是损失函数的梯度。
- 如果不知道什么是梯度下降的,可以看一下这篇文章:机器学习入门教学——梯度下降、梯度上升_恣睢s的博客-CSDN博客
- 损失函数其实就是神经网络里的标准和期望的标准相差多少的定量表达。(现有模型与期望模型的质量差距)
- 损失函数越小,现有模型就越逼近期望模型,现有模型的精度也就越高。
- 【注】损失函数和代价函数可以看作是两个概念不同的名字,但代表的函数和作用完全一样,通常可以互相替换使用,没有实质区别。
- 损失函数该如何设计呢?这里有三种方法:最小二乘法、极大似然估计法、交叉熵法。
- 机器学习入门教学——损失函数(最小二乘法)
- 机器学习入门教学——损失函数(极大似然估计法)
- 机器学习入门教学——损失函数(交叉熵法)
2、交叉熵法
- 交叉熵法是先把模型换成熵(数值),然后再用熵去比较不同模型之间的差异。
- 在了解交叉熵之前,我们先了解以下几个概念。
2.1、信息量
2.1.1、定义
- 信息的作用是消除事件的不确定性,信息量就是信息能消除事件不确定性的程度。
- 例如:
- 掷骰子猜点数时,告诉你一个消息再猜点数。下面三条消息消除不确定性的程度是逐渐增大的,其消息量也是逐渐增大的。

- 我们分别来看上面三条消息发生的概率:
- 骰子的点数大于0:P=1
- 骰子的点数大于3:P=1/2
- 骰子的点数是5:P=1/6
- 我们会发现这些消息发生的概率是逐渐减小的。
- 所以,信息量的大小与信息发生的概率成反比。概率越大,信息量越小;概率越小,信息量越大。
- 设信息描述的事件为x,其发生的概率为P(x),则信息量的公式为:
-
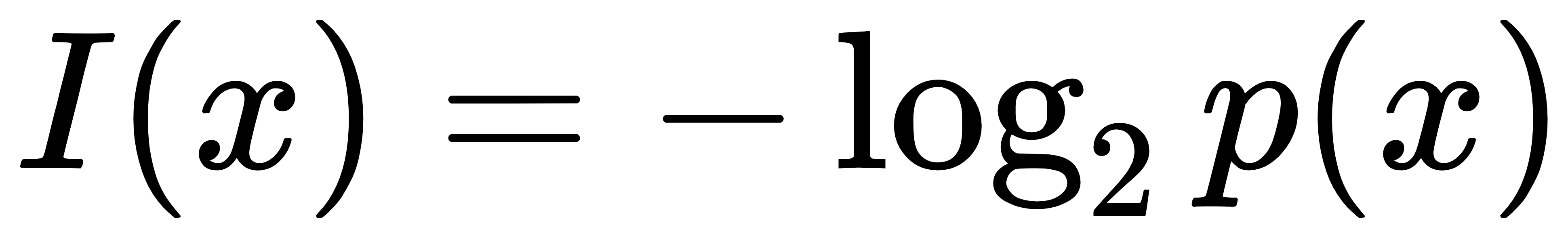 (具体怎么来的就不阐述了),单位为:比特bit
(具体怎么来的就不阐述了),单位为:比特bit
-
2.1.2、计算
- 假设,我们现在要给计算机输入一个十六位的数据。在输入数据之前,这16位数据都可以取0或1,这个数据的概率就是
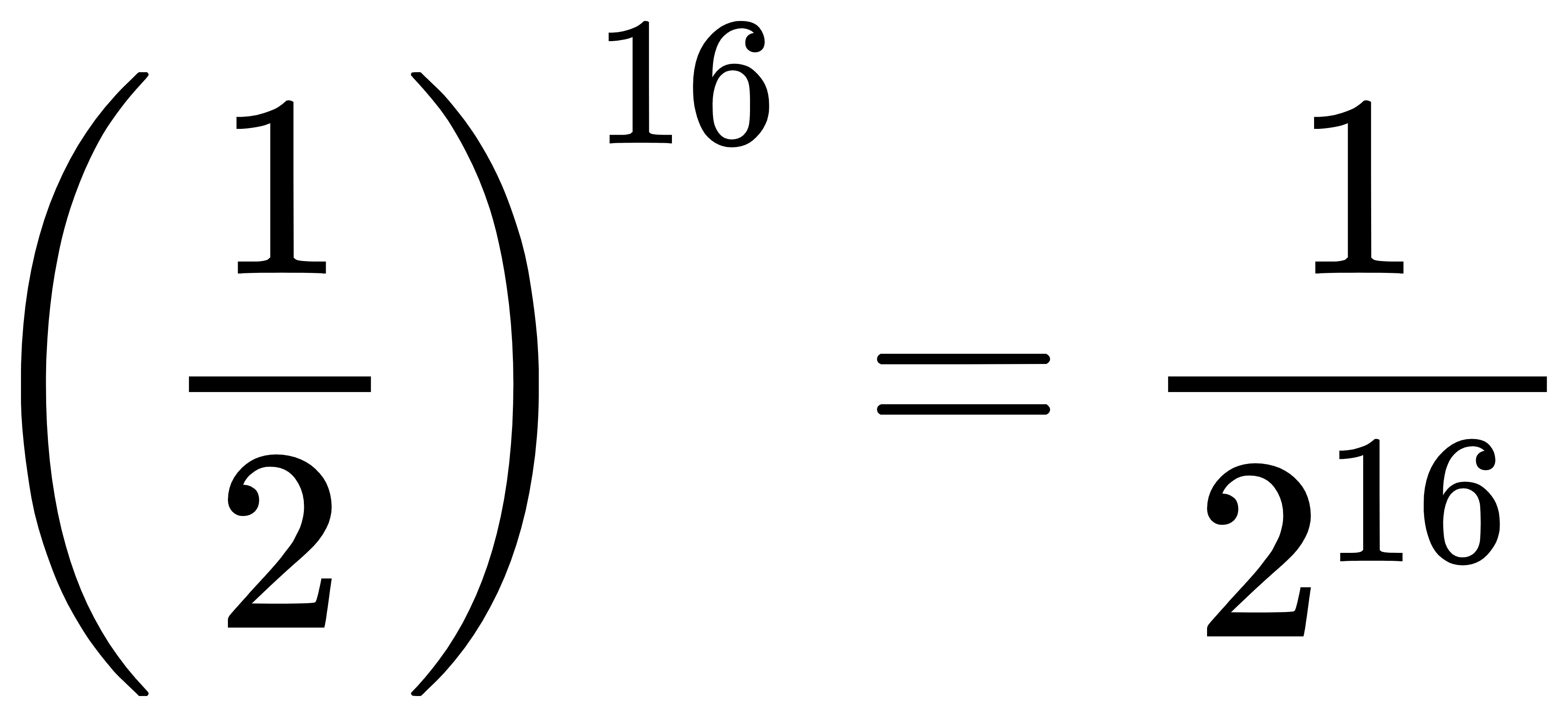 。当输入这个数据后,这个数据是已知的了,它的概率就变成了1。那这个数据的信息量是多少呢?
。当输入这个数据后,这个数据是已知的了,它的概率就变成了1。那这个数据的信息量是多少呢? 
- 这个数据的信息量为16比特。
2.2、信息熵
2.2.1、定义
- 信息量是衡量某个具体的事件,而信息熵是衡量整个系统中的所有事件,即一个系统从原来的不确定到确定难度有多大。
- 信息熵也称为熵,可以表示为所有信息量的期望。所以,信息熵的公式为:
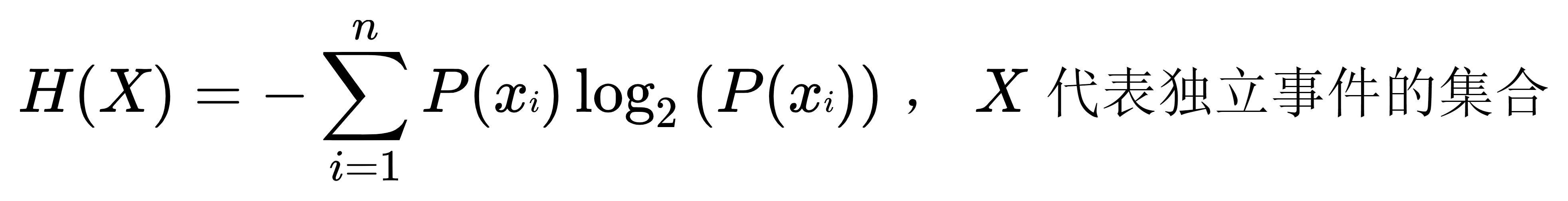 ,单位为:比特
,单位为:比特
- 熵代表了随机变量的不确定性(即混乱程度)。熵越大,代表随机变量的不确定性越大。当变量可取值的种类一定时,其取每种值的概率分布越平均,其熵值越大。
2.2.2、计算
- 假设我们要预测一场球赛的输赢,求它的信息熵。已知法国队赢球的概率是99%,中国队赢球的概率是1%。

- 法国队赢球的信息量为:
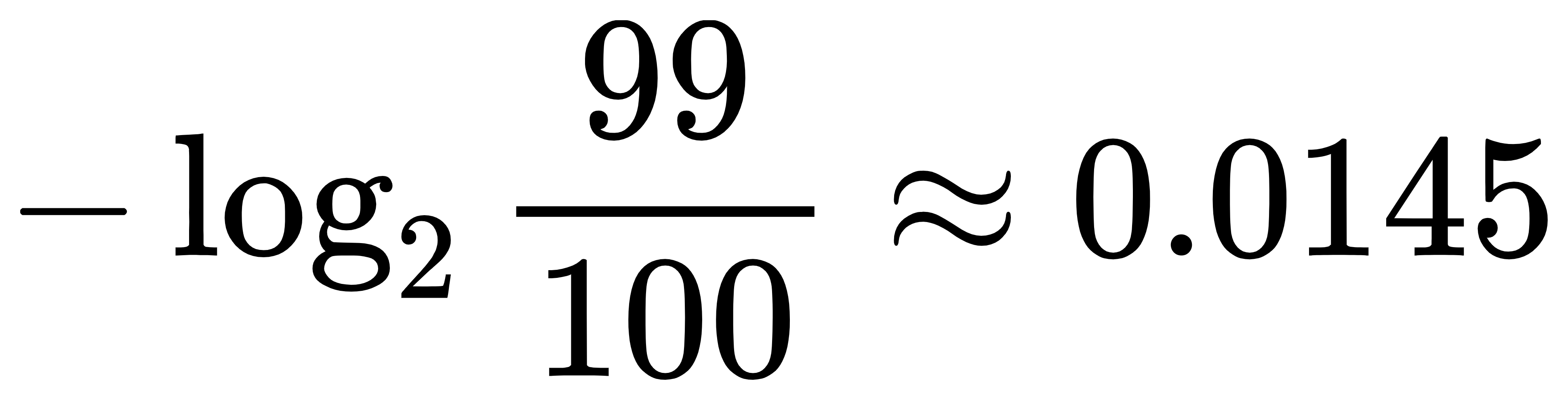
- 中国对赢球的信息量为:
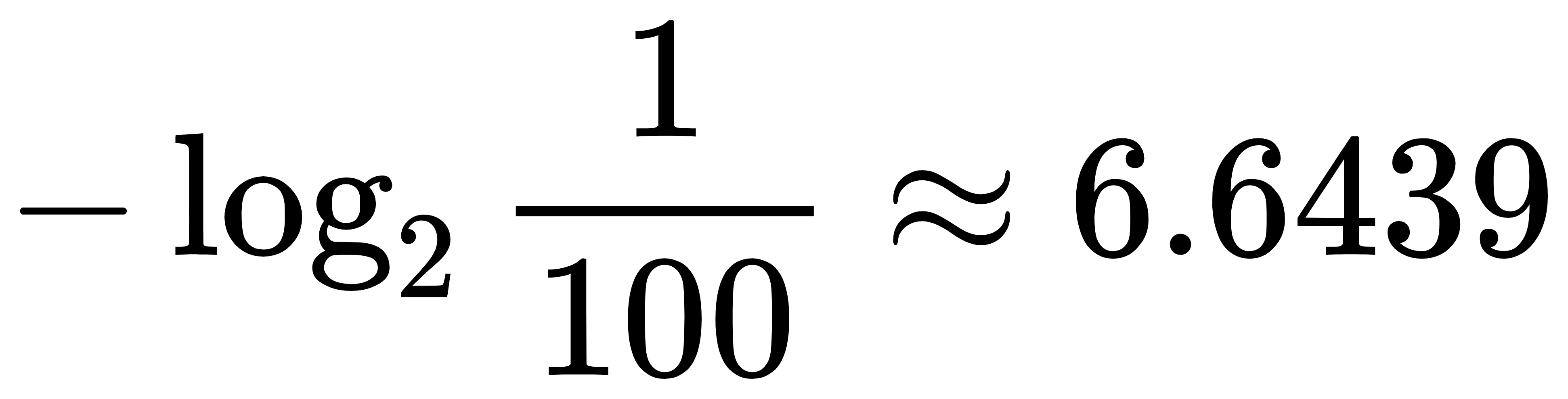
- 信息熵为:
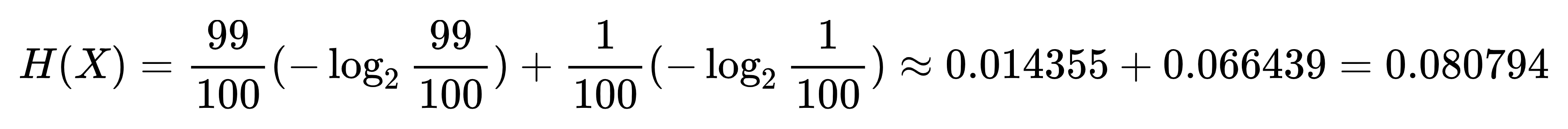
2.3、相对熵(KL散度)
- 比较两个模型,就可以把两个模型的的熵计算出来,再直接比较它们的熵。但是期望模型是未知的,无法直接求熵。那就不得不提到相对熵了。
- 如果对于同一个随机变量X,有两个单独的概率分布P(X)和Q(X),则我们可以使用KL散度来衡量这两个概率分布之间的差异。
- 例如:下面有两个模型的概率分布。
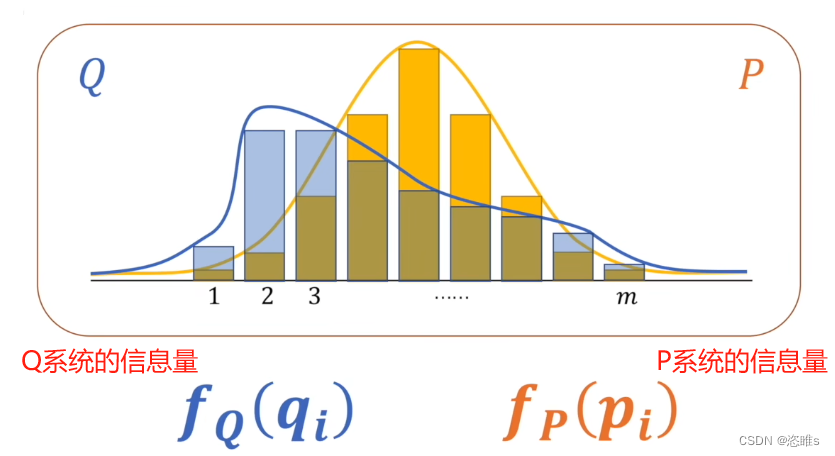
- 以下就是它们相对熵的计算公式:
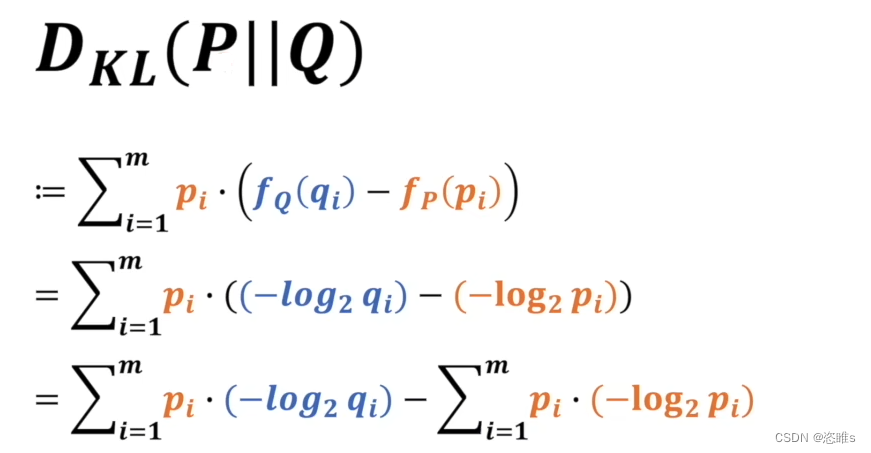 ,其中
,其中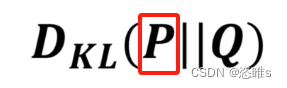 P在前,表示以P系统为基准去考虑P和Q相差多少。
P在前,表示以P系统为基准去考虑P和Q相差多少。- 【注】以P或以Q为基准性质是不同的。
- 其实就是P、Q系统中对应事件的信息量的差值,再求整体期望。
- 如果Q和P相等,那相对熵就为0。简单来说,就是Q要达到和P一样的分布的话,还差了多少信息量。
- 观察发现,
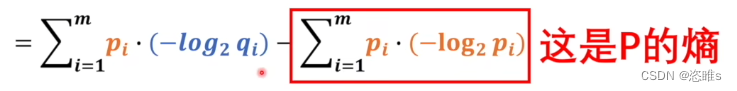 ,P作为基准时熵是不变的,只需要考虑前面一部分。
,P作为基准时熵是不变的,只需要考虑前面一部分。 - 而前面一部分就是交叉熵了,
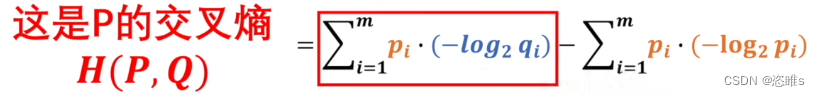
2.4、交叉熵
- 我们已经知道,KL散度 = 交叉熵 - 信息熵
- 交叉熵的公式表示为:
- 由结论可知,KL散度一定是大于等于0的。所以交叉熵是一定大于等于信息量,并且大于0的。(不用深究原因)
- 这时如果要让Q的概率模型和P的概率模型非常接近的话,就要找到交叉熵的最小值。也就是说交叉熵本身就可以作为损失函数。
2.5、运用
- 既然已经知道了交叉熵可以作为损失函数,那么交叉熵中的一些变量在神经网络中应该用什么进行替换呢?
- 我们还是用之前判断图片是不是猫的例子。

- 首先,
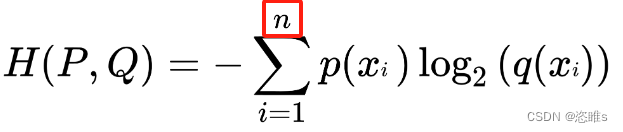 中的n代表输入图片的数量。
中的n代表输入图片的数量。 - 因为P为基准,也就是被比较的模型,所以P是理想模型。而Q是比较的模型,也就是现有模型。那么其中的
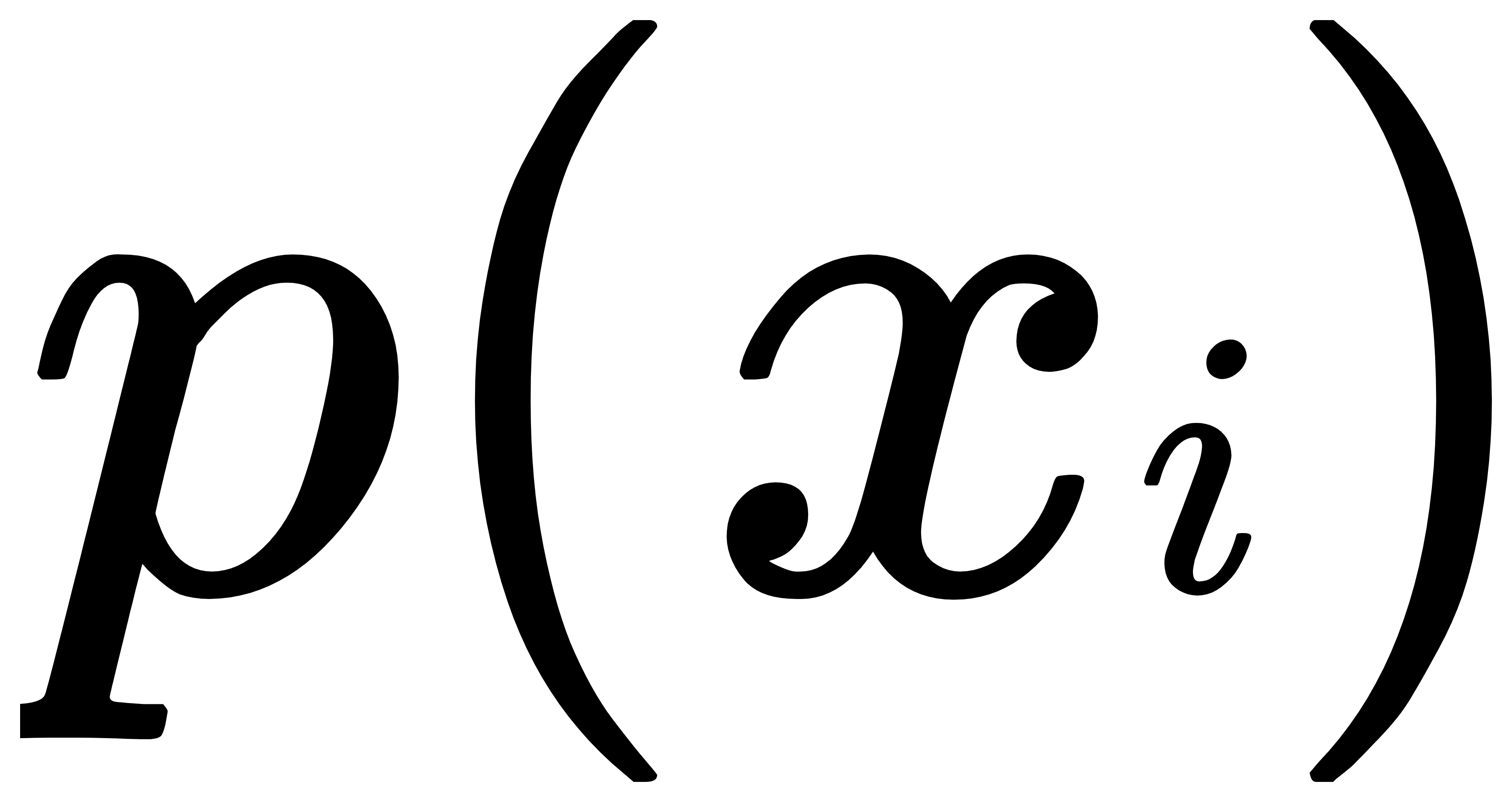 就应该是
就应该是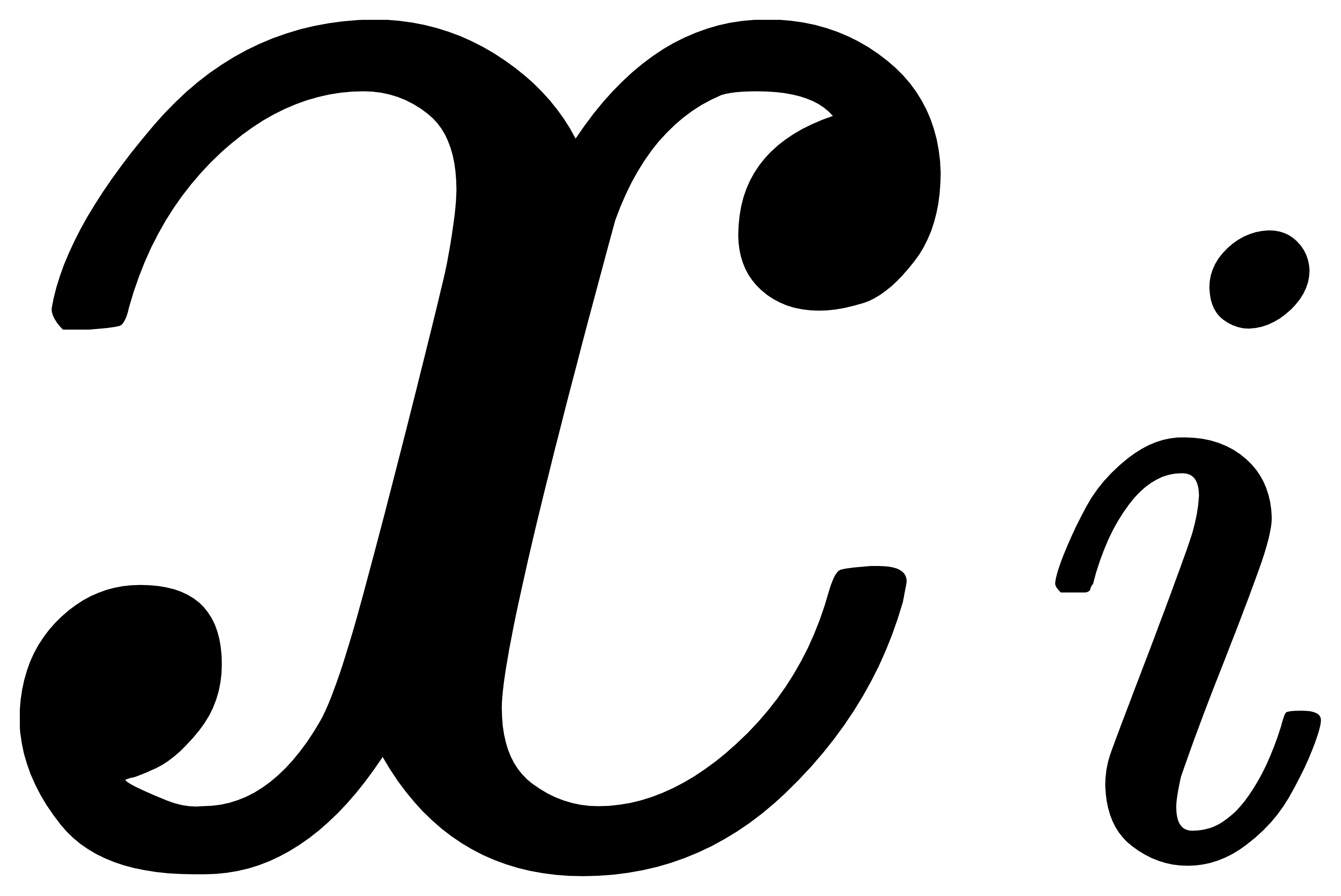 是猫和不是猫的概率,
是猫和不是猫的概率,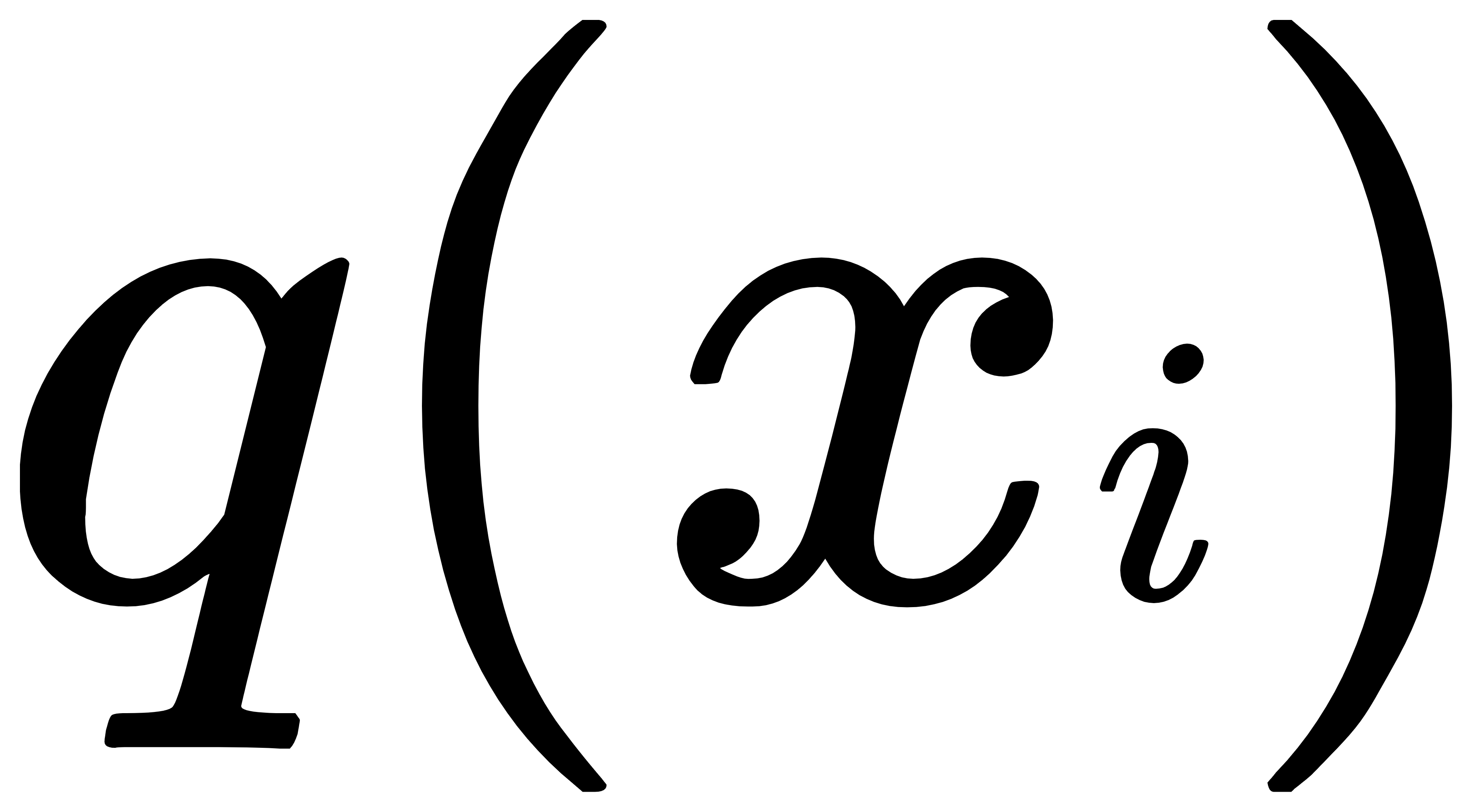 就应该是
就应该是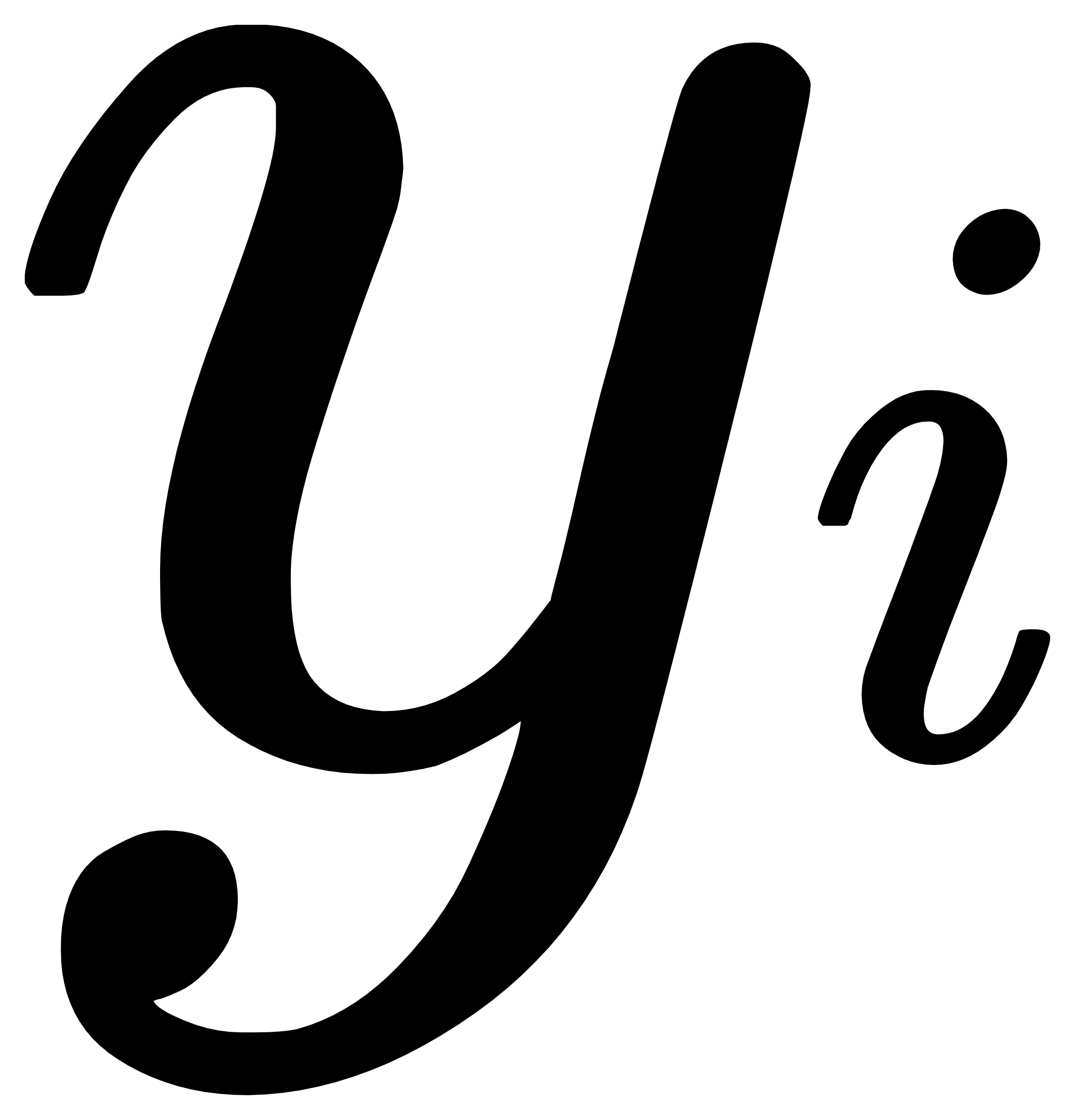 是猫和不是猫的概率。
是猫和不是猫的概率。 - 转换之后就是:
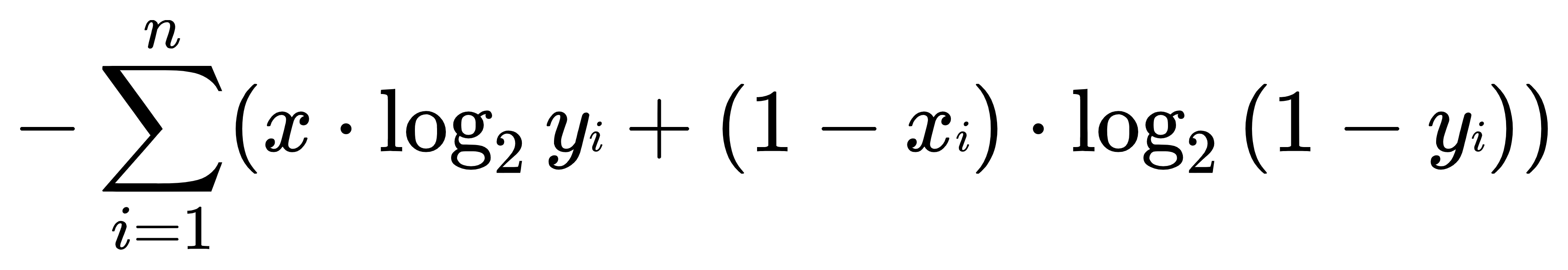
- 这个公式和极大似然估计作为损失函数的公式是一样的。
3、交叉熵法和极大似然估计法的区别
- 虽然两者在形式上是相同的,但是在物理层面还是有很大区别的。
- 极大似然估计中引入log是为了把连乘换做连加,底数为几是无所谓的;而交叉熵中log以2为底是定义中给出的,是固定的,它代表最后计算出来的单位是比特。
- 极大似然估计法本来是求最大值,只是为了适应损失函数才加了个负号改成求最小值;而交叉熵的负号是定义中给出的。
相关文章:
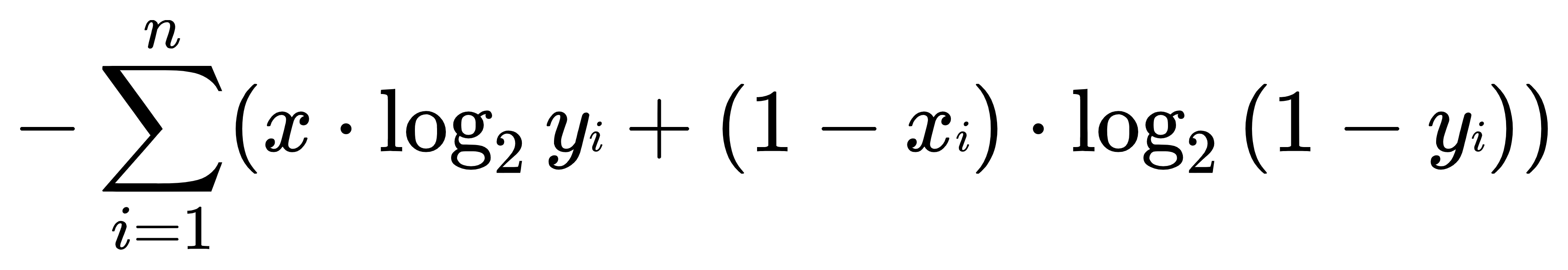
机器学习入门教学——损失函数(交叉熵法)
1、前言 我们在训练神经网络时,最常用到的方法就是梯度下降法。在了解梯度下降法前,我们需要了解什么是损失(代价)函数。所谓求的梯度,就是损失函数的梯度。如果不知道什么是梯度下降的,可以看一下这篇文章:机器学习入…...

pytest一些常见的插件
Pytest拥有丰富的插件架构,超过800个以上的外部插件和活跃的社区,在PyPI项目中以“ pytest- *”为标识。 本篇将列举github标星超过两百的一些插件进行实战演示。 插件库地址:http://plugincompat.herokuapp.com/ 1、pytest-html࿱…...

基于51单片机多路DTH11温湿度检测控制系统
一、系统方案 1、本设计采用51单片机作为主控器。 2、DHT11采集温度度,支持3路温度度,液晶1602显示。 3、按键设置报警阀值。 4、系统声光报警。 二、硬件设计 原理图如下: 三、单片机软件设计 1、首先是系统初始化 //初始化LCD*********…...

宝塔重装注意事项
欢迎关注我的公众号:夜说猫,让一个贫穷的程序员不靠打代码也能吃饭~ 前言 宝塔8.0版本,宝塔卸载重装,或者重装Linux系统后重新安装宝塔也适用。 不能上来直接就执行安装宝塔脚本,除非之前没有安装过宝塔。 步骤 1、…...
【MySQL】 MySQL的增删改查(进阶)--壹
文章目录 🛫数据库约束🌴约束类型🎋NOT NULL约束🎍UNIQUE:唯一约束🌳DEFAULT:默认值约束🎄PRIMARY KEY:主键约束🍀FOREIGN KEY:外键约束…...

Map<K,V>的使用和List学习
Map Map是一种专门用来进行搜索的容器或者数据结构,其搜索的效率与其具体的实例化子类有关。对于静态类型的查找来说,一般直接遍历或者用二分查找【不会对区间进行插入和删除操作】 而在现实生活中的查找比如: 根据姓名查询考试成绩通讯录…...

Flask实现Web服务调用Python程序
Flask实现Web服务调用Python程序_flask调用python程序_小白白程序员的博客-CSDN博客 【小沐学Python】Python实现Web服务器(Flask入门)_python flask web开发_爱看书的小沐的博客-CSDN博客...

步步为营,如何将GOlang引用库的安全漏洞修干净
文章目录 引场景构建第一步、直接引用的第三方库升级修复策略1.确认是否为直接引用的第三方库2.找到需要升级的版本是否为release版本 第二步、间接引用的第三方库升级修复策略那么问题来了,我们这么间接引用库的对应的直接引用库是哪个呢? (…...

as-if-serial与happens-before原则详解
文章目录 前言详解解决多线程下的问题 Happens-before原则总结as-if-serial语义happens-before的例子 前言 "as-if-serial"原则是Java内存模型中的一个重要概念。该规则规定:不管怎么重排序(编译期间的重排序,指令级并行的重排序&…...
:动态蛇形卷积(Dynamic Snake Convolution),实现暴力涨点 | ICCV2023)
基于Yolov8的工业小目标缺陷检测(2):动态蛇形卷积(Dynamic Snake Convolution),实现暴力涨点 | ICCV2023
目录 1.工业油污数据集介绍 1.1 小目标定义 1.2 难点 1.3 工业缺陷检测算法介绍 1.3.1 YOLOv8...

ARM64汇编基础
ARM64汇编基础 主要内容 到目前为止,大部分的移动设备都是64位的arm架构,一直想抽个时间系统学习下,这个周末就专门来学习下。毕竟两天的时间,也只是简单的入门了解下,为后续工作和学习打下基础。 本次学习的主要内容…...
Nodejs 第十六章(ffmpeg)
FFmpeg 是一个开源的跨平台多媒体处理工具,可以用于处理音频、视频和多媒体流。它提供了一组强大的命令行工具和库,可以进行视频转码、视频剪辑、音频提取、音视频合并、流媒体传输等操作。 FFmpeg 的主要功能和特性: 格式转换:…...

k8s集群部署es
集群内创建需要用到存储,此处举例使用腾讯云cfs共享存储 内存limits限制不需要加,否则会经常内存溢出导致es集群故障 apiVersion: apps/v1 kind: StatefulSet metadata:name: es7-clusternamespace: elasticsearch spec:serviceName: es-clusterreplica…...

学习记忆——宫殿篇——记忆宫殿——记忆桩——火车+外院+客厅+卧室
护板 警示灯 烟筒 采集箱 司炉室 桥 电线杆 棚顶 车厢 护栏 植物 石阶 水泥台 竹门 树干 躺椅 柱子 墙 池 洞 方灯 枕头 树 浴池 墙 射灯 藤条 浴巾框 耳环 窗户 灯 沙发 壁炉 吊灯 兵马俑 门 石佛 沙发椅 圆木 弧形木箱盖 床 窗帘 画板 纸伞 花 沙发背 颜料 抽屉...
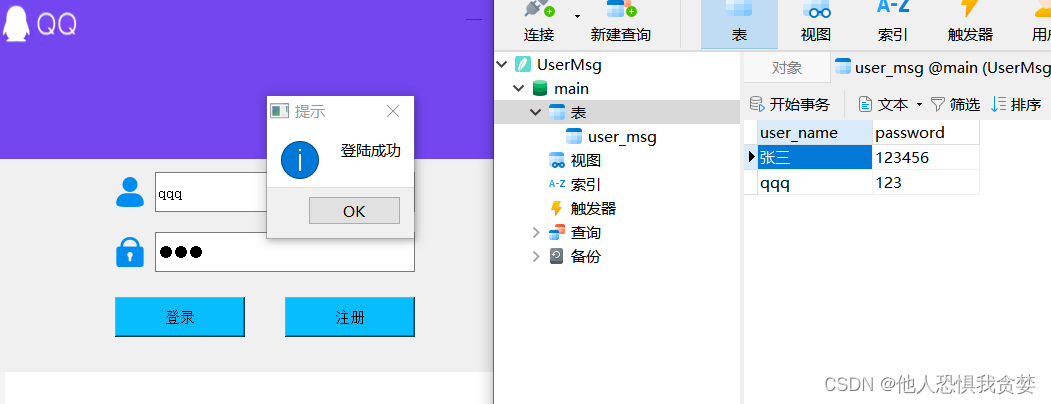
QT用户登录注册,数据库实现
登录窗口头文件 #ifndef LOGINUI_H #define LOGINUI_H#include <QWidget> #include <QLineEdit> #include <QPushButton> #include <QLabel> #include <QMessageBox>#include <QSqlDatabase> //数据库管理类 #include <QSqlQuery> …...
——像元二分法计算月度植被覆盖度(MODIS))
GEE学习总结(9)——像元二分法计算月度植被覆盖度(MODIS)
像元二分法计算植被覆盖度 通过MODIS的NDVI数据集MOD13Q1和像元二分法计算植被覆盖度 var multi_NDVI ee.ImageCollection(MODIS/006/MOD13Q1).filterDate(2015-06-01, 2016-09-01).select(NDVI).max().divide(10000).clip(geometry);var ndviVis {min: 0.0,max: 1,palette…...

RabbitMQ用户命令_策略_日志
RabbitMQ相关安装 Centos离线安装RabbitMQ并开启MQTT Docker安装rabbitMQ RabbitMQ集群搭建和测试总结_亲测 Docker安装RabbitMQ集群_亲测成功 RabbitMQ创建管理员命令 #查看当前用户命令: rabbitmqctl list_users#创建用户和密码 rabbitmqctl add_user admin…...

停车场系统、智慧城市停车、智慧社区、物业管理、新能源充电、人脸门禁 uniapp 系统源码
1. 智慧停车 支持模式 封闭性单个停车场路边停车(车位级管理)大小场(场中场),多场子并行或嵌套 所有者模式 统一平台管理总平台下子账号(区域代理)自建场地资源,自行维护数据总平台下子账号(区域代理)再分配和单个停车场管理人员(物业管理/维保/保安/财务…...

Linux磁盘管理
物理设备的命名规则 在linux系统中一切都是文件,硬件设备也不例外。即然是文件,就必须有文件名称。系统内核中的udev设备管理器会自动把硬件名称规范起来,目的是让用户通过设备文件的名字可以看出设备大致的属性以及分区信息等;在…...

vue学习之vue cli创建项目
安装 node.js https://nodejs.org/en 安装 vue cli npm install -g @vue/cli --registry=https://registry.npm.taobao.org创建项目 执行创建命令,回车vue create vue-cli-learning选择 “Manually select features”,回车 “空格” 关闭 Linter / Formatter 选项,回车...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...