python随手小练
题目:
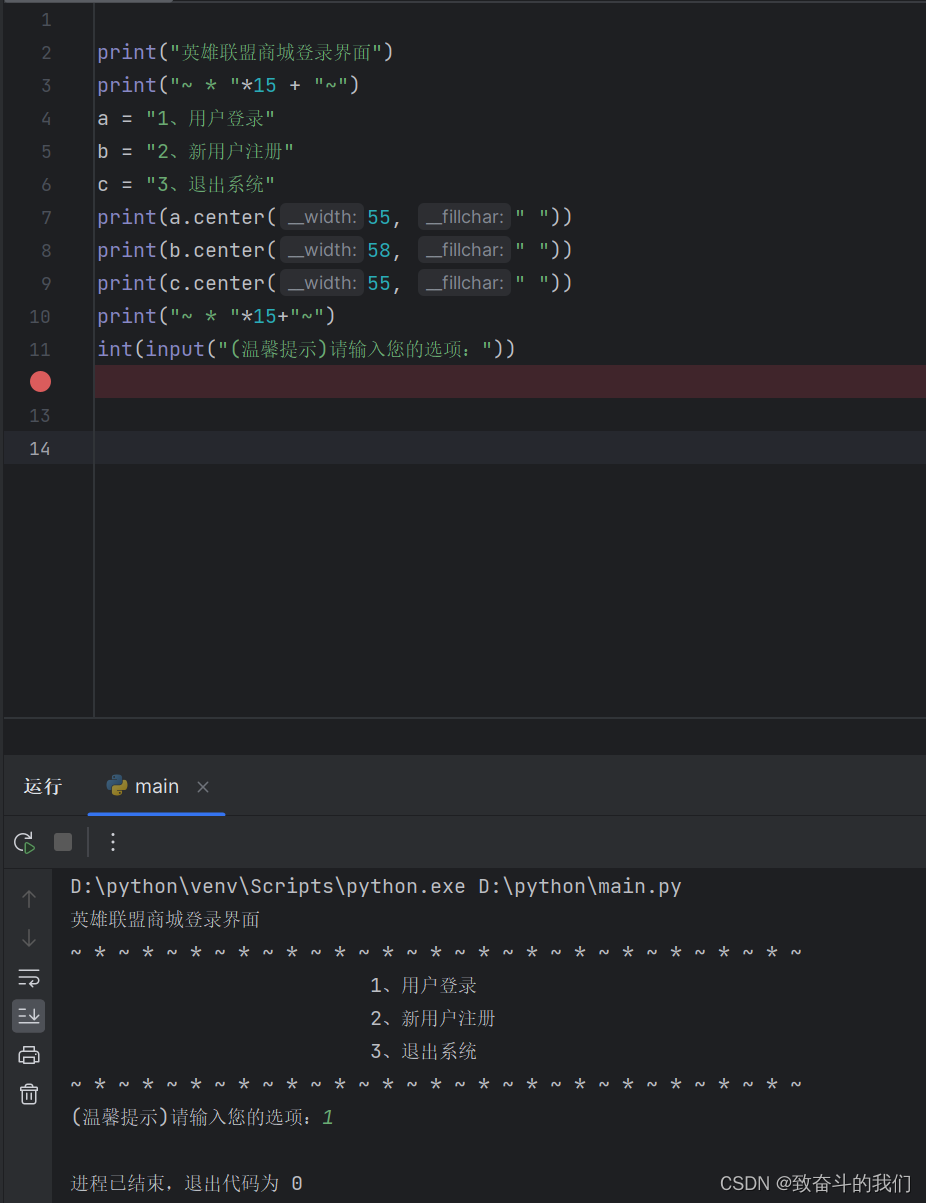
使用python做一个简单的英雄联盟商城登录界面

具体操作:
print("英雄联盟商城登录界面")
print("~ * "*15 + "~") #找其规律
a = "1、用户登录"
b = "2、新用户注册"
c = "3、退出系统"
print(a.center(55, " ")) #使其居中,其余用空格补齐
print(b.center(58, " "))
print(c.center(55, " "))
print("~ * "*15+"~")
int(input("(温馨提示)请输入您的选项:")) #输入用户选项
本次只是简单的搭载界面,后续操作根据学习持续更新
结果展示:
相关文章:

python随手小练
题目: 使用python做一个简单的英雄联盟商城登录界面 具体操作: print("英雄联盟商城登录界面") print("~ * "*15 "~") #找其规律 a "1、用户登录" b "2、新用户注册" c "3、退出系统&quo…...

MySQL——函数和流程控制
2023.9.21 函数 含义:一组预先编译好的SQL语句的集合,理解成批处理语句。 提高代码的重用性简化操作减少了编译次数并且减少了和数据库服务器的连接次数,提高了效率 与存储过程的区别: 存储过程:可以有0个返回&am…...

【Vue3 源码讲解】nextTick
nextTick 是 Vue 3 中用于异步执行回调函数的函数,它会将回调函数延迟到下一个微任务队列中执行。其中,Vue 更新 DOM 是异步的。下面是对 nextTick 函数的详细解释: export function nextTick<T void, R void>(this: T,fn?: (this:…...

什么是ATR,在聚宽量化平台如何计算ATR
海龟们使用两种资金管理方法。首先,我们把头寸分成一个个小块。这样,即使一笔交易赔了钱,我们损失的也只是一个头寸的一部分。里奇和比尔把这些小块称作头寸单位。其次,我们使用里奇和比尔发明的一种创新性的头寸规模决定方法。这…...
Python 爬虫实战之爬淘宝商品并做数据分析
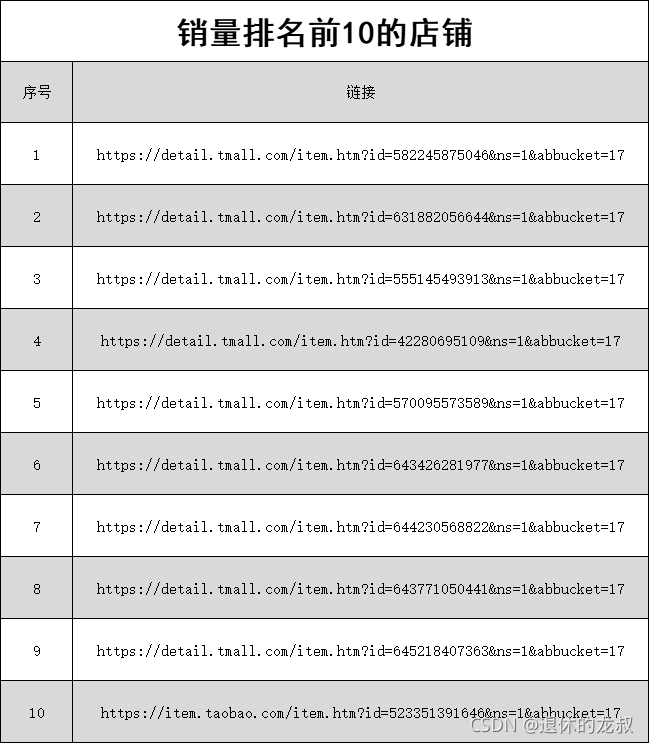
前言 是这样的,之前接了一个金主的单子,他想在淘宝开个小鱼零食的网店,想对目前这个市场上的商品做一些分析,本来手动去做统计和分析也是可以的,这些信息都是对外展示的,只是手动比较麻烦,所以…...
)
Python爬虫-requests.exceptions.SSLError: HTTPSConnectionPool疑难杂症解决(1)
前言 本文是该专栏的第7篇,后面会持续分享python爬虫案例干货,记得关注。 在爬虫项目开发中,偶尔可能会遇到SSL验证问题“requests.exceptions.SSLError: HTTPSConnectionPool(host=www.xxxxxx.com, port=443): Max retries exceeded with url ...”。亦或是验证之后的提示…...

12:STM32---RTC实时时钟
目录 一:时间相关 1:Unix时间戳 2: UTC/GMT 3:时间戳转化 二:BKP 1:简历 2:基本结构 三: RTC 1:简历 2: 框图 3:RTC基本结构 4:RTC操作注意 四:案例 A:读写备份寄存器 1:连接图 2: 步骤 3: 代码 B:实时时钟 1:连接图 2:函数介绍 3:代码 一:时间相关 1:Un…...
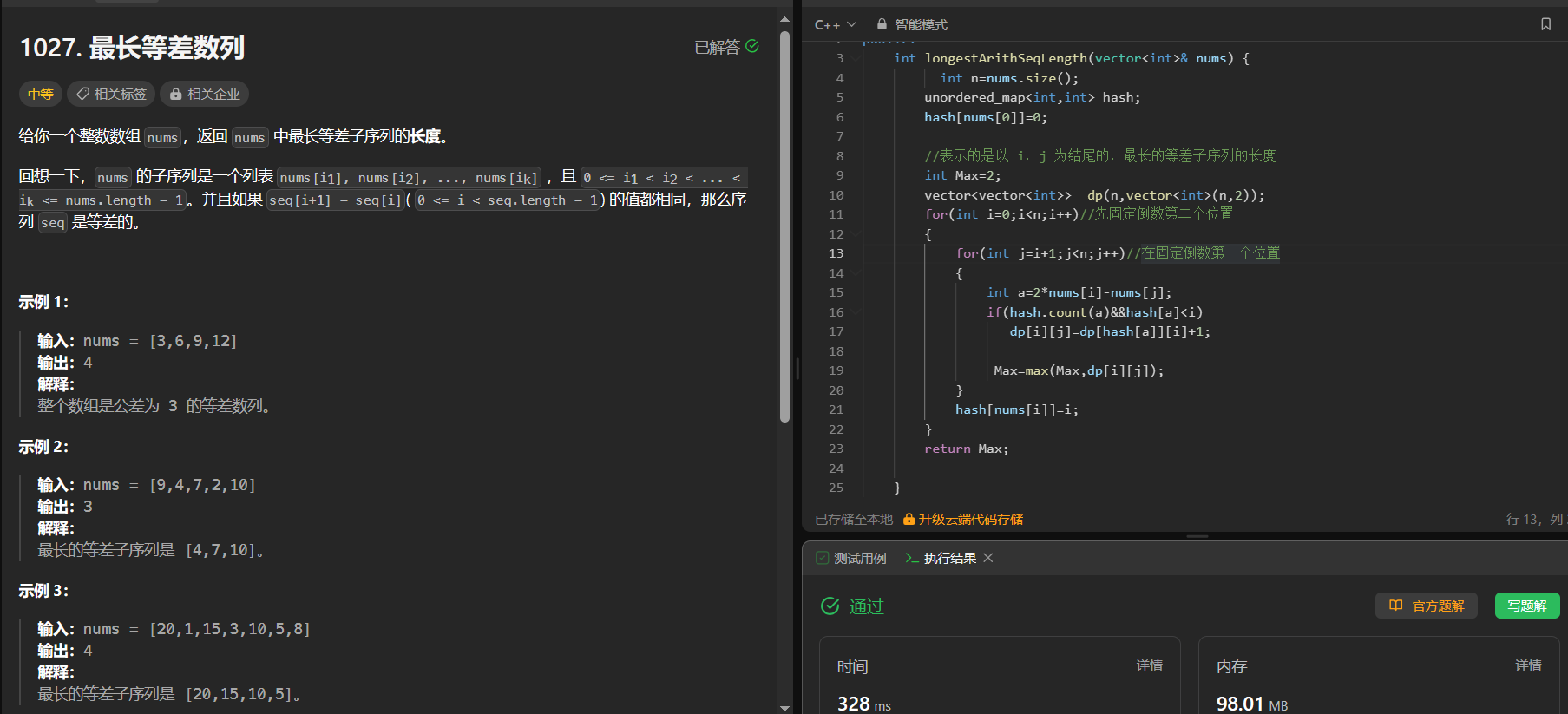
【动态规划刷题 16】最长等差数列 (有难度) 等差数列划分 II - 子序列
1027. 最长等差数列 https://leetcode.cn/problems/longest-arithmetic-subsequence/ 给你一个整数数组 nums,返回 nums 中最长等差子序列的长度。 回想一下,nums 的子序列是一个列表 nums[i1], nums[i2], …, nums[ik] ,且 0 < i1 <…...
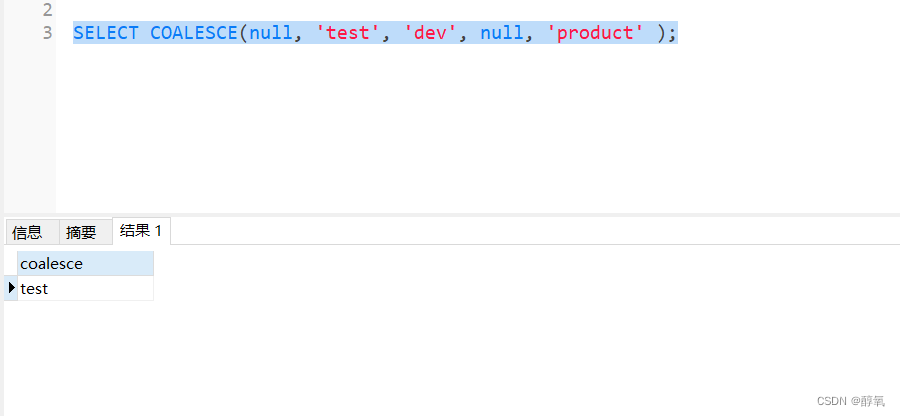
【postgresql】替换 mysql 中的ifnull()
数据库由mysql 迁移到postgresql,程序在执行查询时候报错。 HINT: No function matches the given name and argument types. You might need to add explicit type casts. CONTEXT: referenced column: ifnull 具体SQL: SELECT ifnull(phone,) FROM c_user p…...
)
单例模式(懒汉式,饿汉式,变体)
单例模式,用于确保一个类只有一个实例,并提供一个全局访问点以访问该实例。 饿汉式(Eager Initialization) 程序启动时就创建实例 #include <iostream> class SingletonEager { private:static SingletonEager* instanc…...

Java Lambda表达式:简洁且强大的函数式编程工具
Lambda表达式是Java 8及以后版本中引入的一种函数式编程特性。它是一种匿名函数,允许开发人员以简洁和易读的方式编写代码,并且可以作为参数传递给方法或存储在变量中。Lambda表达式的基本语法如下:(parameters) -> expression,…...
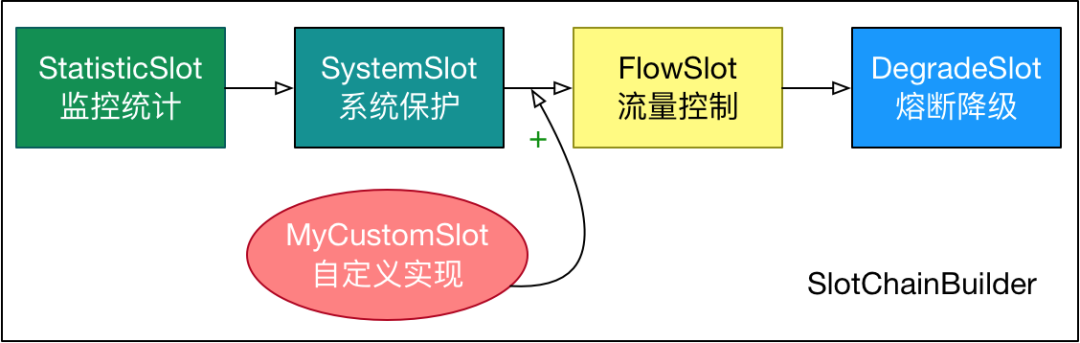
开源框架中的责任链模式实践
作者:vivo 互联网服务器团队-Wang Zhi 责任链模式作为常用的设计模式而被大家熟知和使用。本文介绍责任链的常见实现方式,并结合开源框架如Dubbo、Sentinel等进行延伸探讨。 一、责任链介绍 在GoF 的《设计模式》一书中对责任链模定义的:将…...
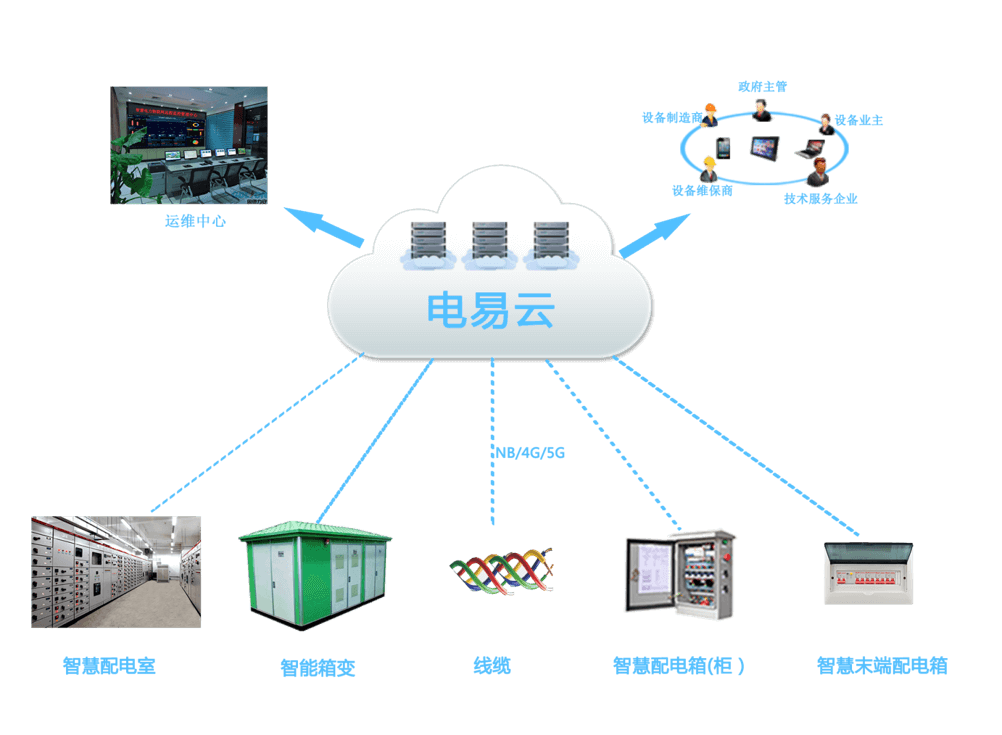
智能配电系统:保障电力运行安全、可控与高效
智能配电系统是一种先进的电力分配技术,它通过智能化、数字化和网络化等方式,有效地保障了电力运行的安全、可控和高效。 力安科技智能配电系统是在配电室(含高压柜、变压器、低压柜)、箱式变电站、配电箱及动力柜(…...
-每天学习10个知识)
MySQL学习系列(11)-每天学习10个知识
目录 1. 数据库设计的关键因素2. 使用存储过程和函数来提高性能和可重用性3. MySQL性能优化4. 使用视图简化查询和提供数据安全性5. 数据库备份和恢复策略的重要性和实践经验6. 在分布式系统中保证数据一致性和可用性7. 理解MySQL的复制和其在实际应用中的作用8. 使用游标进行分…...
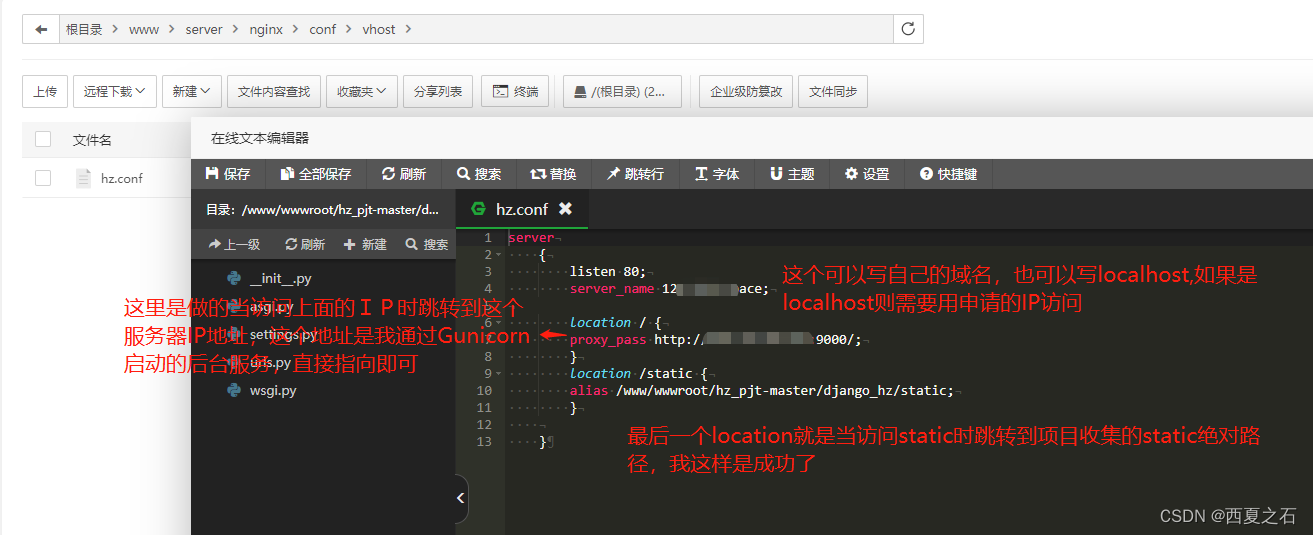
如何通过Gunicorn和Niginx部署Django
本文主要介绍如何配置Niginx加载Django的静态资源文件,也就是Static 1、首先需要将Django项目中的Settings.py 文件中的两个参数做以下设置: STATIC_URL /static/ STATIC_ROOT os.path.join(BASE_DIR, static) 然后在宝塔面板中执行python manage.…...
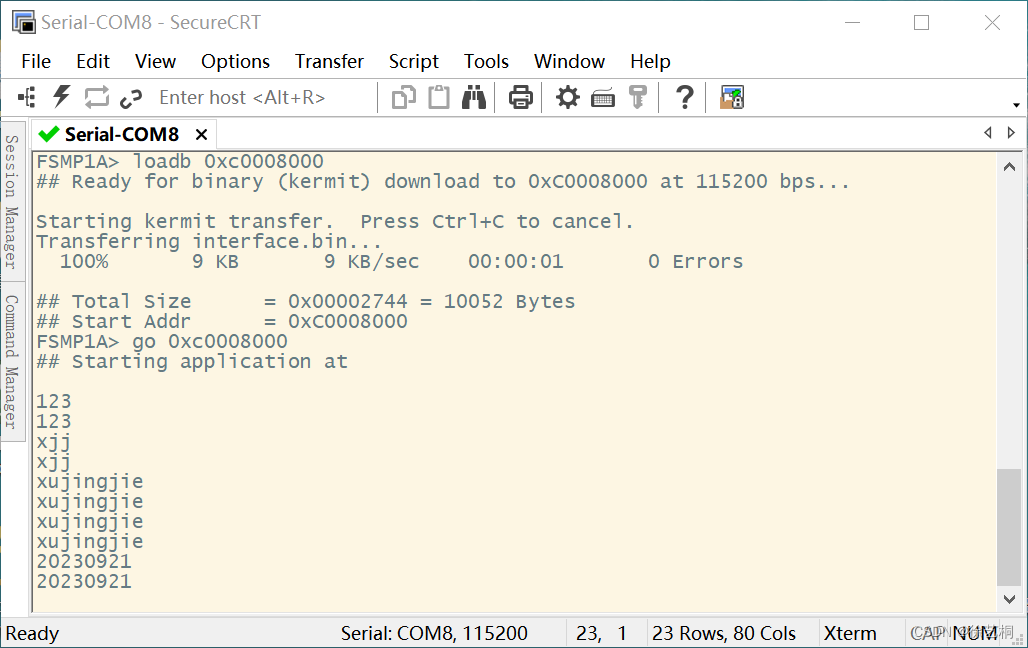
C语言 cortex-A7核UART总线实验
一、C 1)uart4.h #ifndef __UART4_H__ #define __UART4_H__ #include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_uart.h&quo…...

asp.net C#免费反编译工具ILSpy
在维护一个没有源码的C#项目,只能反编译了。 项目主页 https://github.com/icsharpcode/ILSpy 使用方法 中文界面使用简单,把你要反编译的dll拖过去就可以了。好使!!!...

演讲实录:DataFun 垂直开发者社区基于指标平台自主洞察北极星指标
在7月14日举办的 Kyligence 用户大会的数智新应用论坛上,DataFun COO 杜颖女士为大家带来了《垂直开发者社区基于指标平台自主洞察北极星指标》的主题演讲。接下来,我们一起看看 DataFun 如何在没有专门的 IT 团队的情况下,实现对北极星指标的…...
ffmpeg编译 Error: operand type mismatch for `shr‘
错误如下: D:\msys2\tmp\ccUxvBjQ.s: Assembler messages: D:\msys2\tmp\ccUxvBjQ.s:345: Error: operand type mismatch for shr D:\msys2\tmp\ccUxvBjQ.s:410: Error: operand type mismatch for shr D:\msys2\tmp\ccUxvBjQ.s:470: Error: operand type mismatch…...
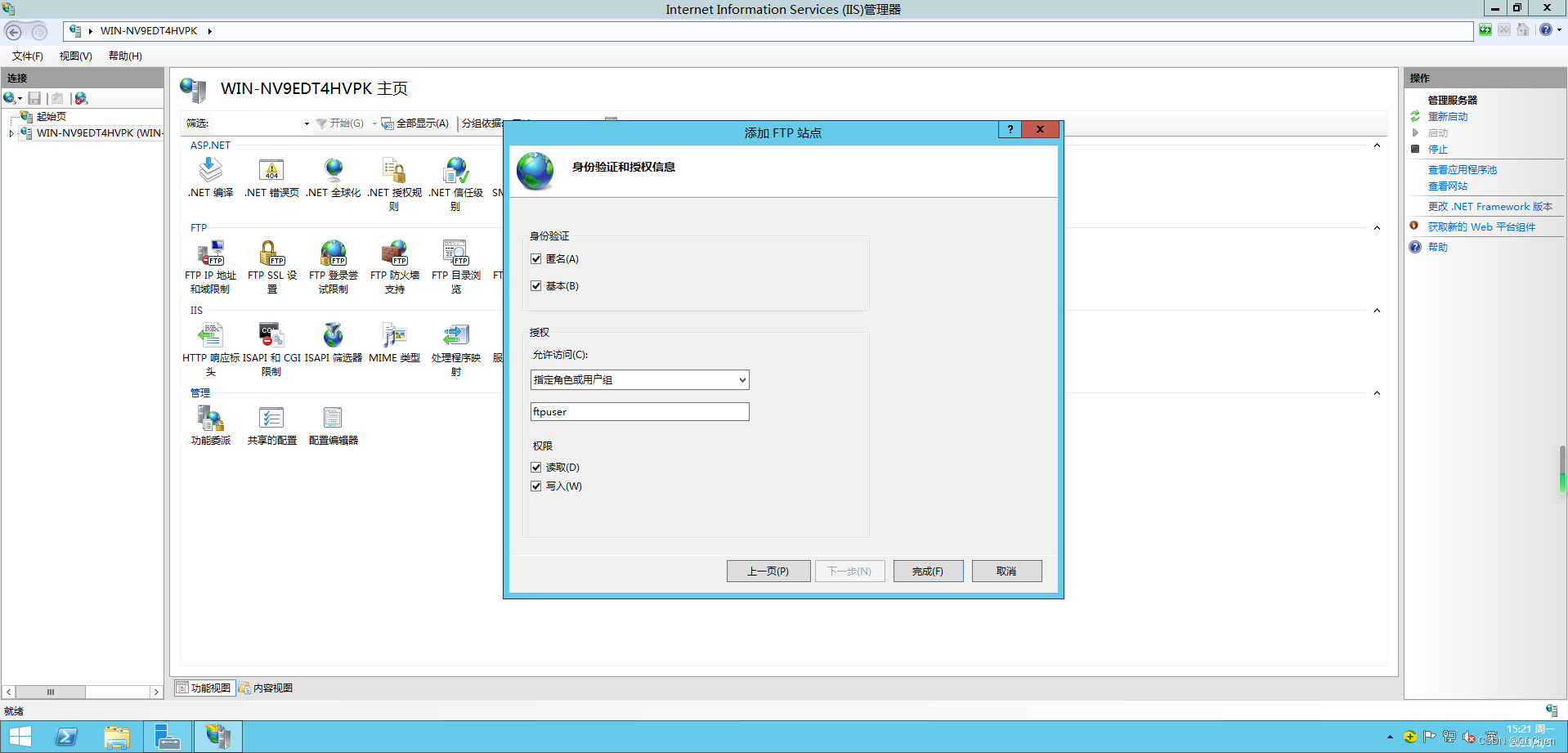
【Windows Server 2012 R2搭建FTP站点】
打开服务器管理器——添加角色和功能 下一步 下一步 下一步 选择FTP服务器,勾上FTP服务和FTP扩展,点击下一步 安装 安装完成关闭 打开我们的IIS服务器 在WIN-XXX主页可以看到我们的FTP相关菜单 右键WIN-XXXX主页,添加FTP站点 输入站点名称-FT…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
