【数据结构】时间、空间复杂度
⭐ 作者:小胡_不糊涂
🌱 作者主页:小胡_不糊涂的个人主页
📀 收录专栏:浅谈数据结构
💖 持续更文,关注博主少走弯路,谢谢大家支持 💖
时间、空间复杂度
- 1. 算法效率
- 3. 时间复杂度
- 3.1 时间复杂度的概念
- 3.2 大O的渐进表示法
- 3.3 推导大O阶方法
- 3.4 常见时间复杂度计算举例
- 4. 空间复杂度

1. 算法效率
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。
时间效率被称为时间复杂度,而空间效率被称作空间复杂度。
时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间。
在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
3. 时间复杂度
3.1 时间复杂度的概念
时间复杂度的定义: 在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。
一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。
但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
3.2 大O的渐进表示法
试计算下面代码中的 func1 基本操作执行了多少次?
void func1(int N){int count = 0;for (int i = 0; i < N ; i++) {for (int j = 0; j < N ; j++) {count++;}}for (int k = 0; k < 2 * N ; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);
}
Func1 执行的基本操作数为:N* N+2* N+10

- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
3.3 推导大O阶方法
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
N = 10 F(N) = 100
N = 100 F(N) = 10000
N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
- 最坏情况:任意输入规模的最大运行次数(上界)
- 平均情况:任意输入规模的期望运行次数
- 最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
3.4 常见时间复杂度计算举例
实例1:
// 计算func2的时间复杂度?void func2(int N) {int count = 0;for (int k = 0; k < 2 * N ; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);}

上述代码的基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
实例2:
// 计算func3的时间复杂度?void func3(int N, int M) {int count = 0;for (int k = 0; k < M; k++) {count++;}for (int k = 0; k < N ; k++) {count++;}System.out.println(count);}

上述代码基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
实例3:
// 计算func4的时间复杂度?void func4(int N) {int count = 0;for (int k = 0; k < 100; k++) {count++;}System.out.println(count);}

上述代码基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
实例4:
// 计算bubbleSort的时间复杂度?void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}

上述代码基本操作执行最好N次,最坏执行了(N*(N-1))/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)
实例5:
// 计算binarySearch的时间复杂度?int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;}
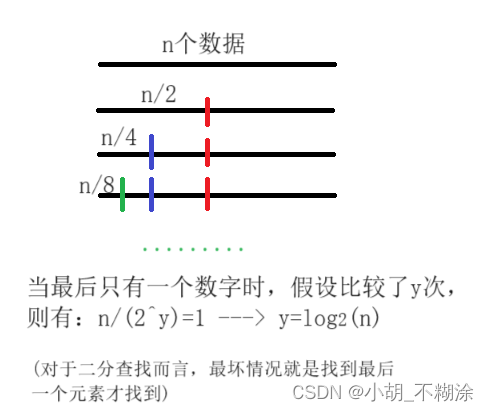
上述代码基本操作执行最好1次,最坏log2(N)次,时间复杂度为 O(log2(N))。
在算法分析中表示是底数为2,对数为N,有些地方会写成lgN。
实例6:
// 计算阶乘递归factorial的时间复杂度?long factorial(int N) {return N < 2 ? N : factorial(N-1) * N;}
通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。
实例7:
// 计算斐波那契递归fibonacci的时间复杂度?int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);}

通过计算分析发现基本操作递归了2^N 次,时间复杂度为O(2^ N)
4. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表法。
实例1:
// 计算bubbleSort的空间复杂度?void bubbleSort(int[] array){for (int end = array.length; end > 0; end--) {boolean sorted = true;//开辟一个空间for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}
使用了常数个额外空间,所以空间复杂度为 O(1)
实例2:
// 计算fibonacci的空间复杂度?int[] fibonacci(int n) {long[] fibArray = new long[n + 1];//开辟了n个空间fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;}动态开辟了N个空间,空间复杂度为 O(N)
实例3:
// 计算阶乘递归Factorial的空间复杂度?long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;}
递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
相关文章:

【数据结构】时间、空间复杂度
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈数据结构 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 时间、空间复杂度 1. 算法效率3. 时…...

Databend 开源周报第 111 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 理解 SHARE END…...
iOS自动化测试方案(一):MacOS虚拟机保姆级安装Xcode教程
文章目录 一、环境准备二、基础软件三、扩展:usb拓展插件 一、环境准备 1、下载VMware虚拟机的壳子,安装并注册软件(可以百度注册码),最新版本:v17 2、下MacOS系统iOS镜像文件,用于vmware虚拟机安装,当前镜…...

vue3 - Vue 项目处理GitHub Pages 部署后 _plugin-vue_export-helper.js 404
GitHub Demo 地址 在线预览 vue3项目打包后部署到github pages 后,预览网站提示下划线开头的一个文件_plugin-vue_export-helper访问不到,网络请求显示404 处理GitHub Pages 部署 _plugin-vue_export-helper.js 404 https://github.com/rollup/rollup/b…...
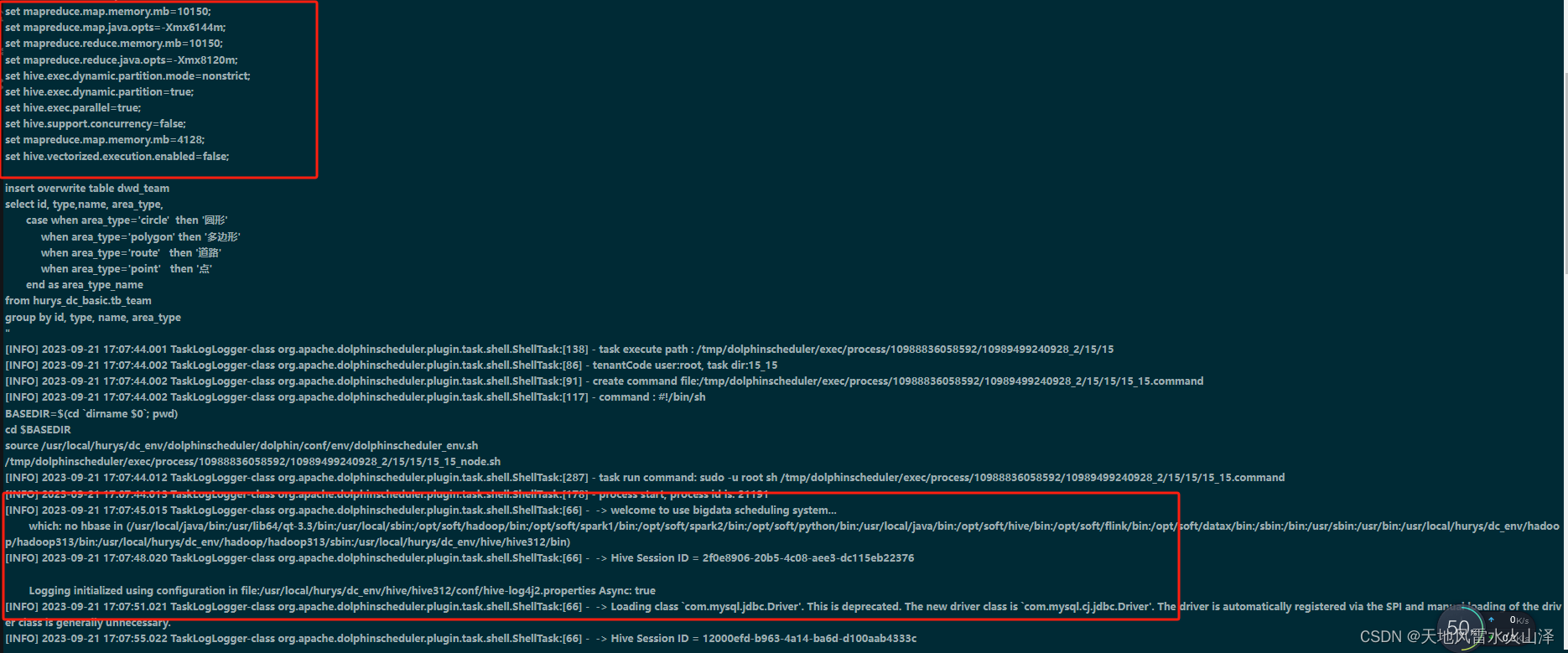
一百八十一、Hive——海豚调度HiveSQL任务时当Hive的计算引擎是mr或spark时脚本的区别(踩坑,附截图)
一、目的 当Hive的计算引擎是spark或mr时,发现海豚调度HQL任务的脚本并不同,mr更简洁 二、Hive的计算引擎是Spark时 (一)海豚调度脚本 #! /bin/bash source /etc/profile nowdatedate --date0 days ago "%Y%m%d" y…...
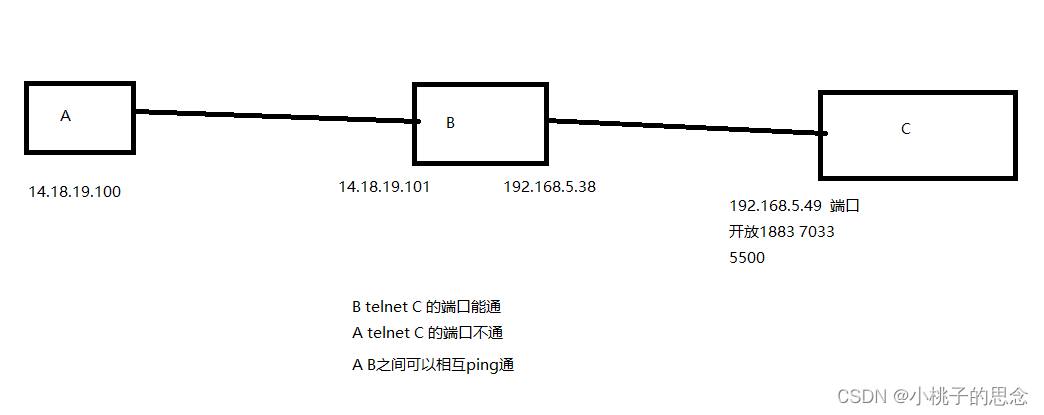
Linux 隔离网段下端口转发
设备在隔离网段下,设置端口转发。使A设备可访问C设备的服务 #!/bin/bash #输出成绩脚本 echo -n "请输入外网服务器的IP地址:" read score sudo iptables -t nat -A PREROUTING -p tcp --dport 1883 -j DNAT --to-destination $score:1883 s…...

【CDN和UDN】CDN和UDN技术特点以及使用场景
内容分发网络(CDN)和用户自定义网络(UDN)是两种不同的网络技术,在选择时,往往不能准备把握具不同的技术特点和应用场景。CDN 主要用于加速内容分发,而 UDN 则主要用于支持用户自定义的网络需求。…...

【Linux】改变缓存路径、清理缓存
写在前面 在做项目的过程中,服务器base路径下空间不足,准备在另一个目录下创建虚拟环境,但在安装的过程中,发现base路径下的空间还是在减少,后来经过学习了解到,pip安装下载依赖包时,会先下载缓…...

python+opencv寻找图片或视频中颜色进行追踪之HSV颜色处理
pythonopencv寻找图片或视频中颜色进行追踪之HSV颜色处理 1.颜色空间转换 import cv2img cv2.imread(1.jpg) # 转换为灰度图 img_gray cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)cv2.imshow(img, img) cv2.imshow(gray, img_gray) cv2.waitKey(0)cv2.cvtColor()用来进行颜色模…...
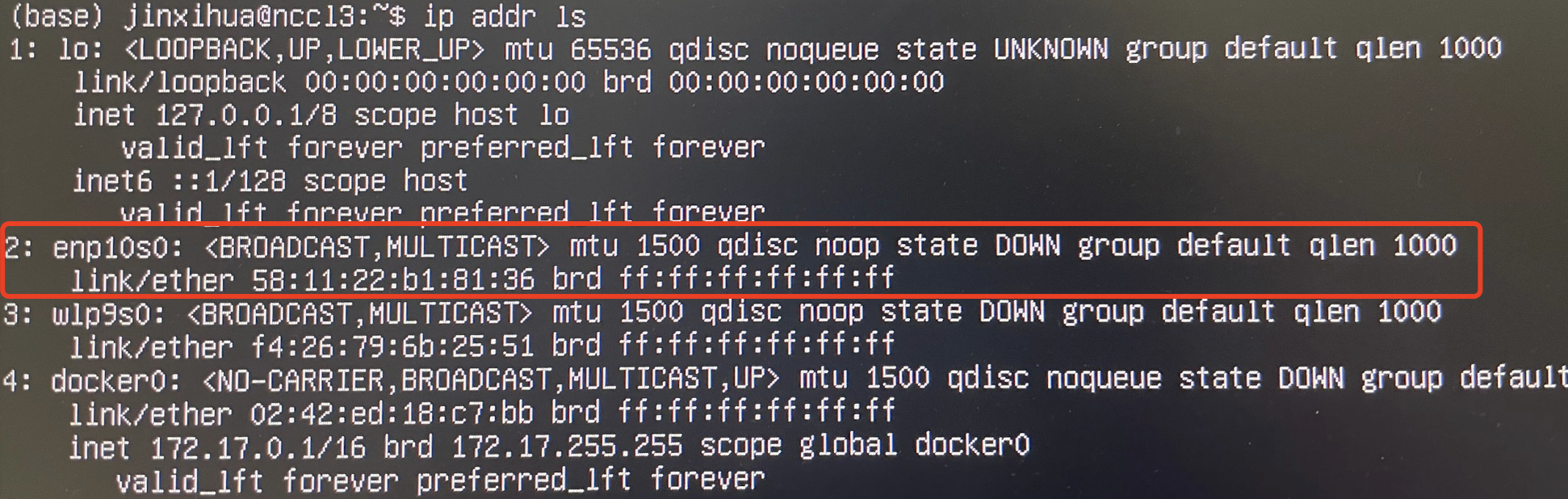
ubuntu 22.04 服务器网卡无IP地址
ssh连接服务器连接不上,提示如下; 连接显示器,ip addr ls 命令查看IP地址,有网卡但没有IP地址 solution: sudo dhclient enp10s0用于通过 DHCP 协议获取网络配置信息并为名为 enp10s0 的网络接口分配 IP 地址,enp1…...
基于SpringBoot的网上点餐系统
目录 前言 一、技术栈 二、系统功能介绍 用户功能模块 管理员功能模块 美食店功能模块 前台首页功能模块 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 系统管理也都将通过计算机进行整体智能化操作,对于网上点餐系统所牵扯的管理及数据保存…...
浅谈xss
XSS 简介 XSS,全称Cross Site Scripting,即跨站脚本攻击,是最普遍的Web应用安全漏洞。这类漏洞能够使得攻击者嵌入恶意脚本代码到正常用户会访问到的页面中,当正常用户访问该页面时,则可导致嵌入的恶意脚本代码的执行,从而达到恶意攻击用户的目的。需要强调的是,XSS不仅…...

悬崖边:企业如何应对网络安全漏洞趋势
在本文中,我们将讨论企业在处理漏洞时面临的挑战,解释安全漏洞是如何引发网络攻击的,以及为什么它会导致不可接受的事件。我们还将分享我们在识别趋势性漏洞方面的经验。 现代信息安全方法正在成为企业的工作流程。例如,不久前&a…...

MyBatis 动态 SQL、MyBatis 标签、MyBatis关联查询
MyBatis 动态 SQL、MyBatis 标签、MyBatis关联查询 1、MyBatis动态 sql 的特性2、MyBatis 标签2.1、if 标签:条件判断2.2、whereif 标签2.3、set 标签2.4、choose(when,otherwise) 语句2.5、trim2.6、MyBatis foreach 标签 3、整合案例3.1、XML3.2、测试类 4、sql 标…...

在Vue中使用Immutable.js
在Vue3中使用Immutable.js 以下是如何在Vue.js中使用Immutable.js的步骤: 首先,需要安装immutable.js。你可以通过npm或yarn来安装: npm install immutable或者 yarn add immutable在你的Vue组件中导入Immutable: import { Ma…...
基于Yolov8的工业端面小目标计数检测(1)
1.端面小目标计数数据集介绍 工业端面小目标计数类别:一类,类别名object 数据集大小:训练集864张,验证集98张 缺陷特点:小目标计数,检测难度大,如下图所示; 1.1 小目标定义 1)以物体检测领域的通用数据集COCO物体定义为例,小目标是指小于3232个像素点(中物体是指…...

1.什么是jwt?jwt的作用是什么?2.jwt的三个部分是什么?三者之间的关系如何?3.JWT运行的流程是什么
1. **什么是JWT?JWT的作用是什么?** JWT(JSON Web Token)是一种用于在不同系统或组件之间传输信息的紧凑且安全的标准。它的作用主要有两个方面: - **身份验证(Authentication)**…...

十三、MySql的视图
文章目录 一、前言二、定义三、为什么使用视图四、基本使用(—)创建视图(二)案例1.修改了视图,对基表数据有影响2.修改了基表,对视图有影响3.删除视图 五、视图规则和限制 一、前言 通过视图,可…...
MFC扩展库BCGControlBar Pro v33.6亮点 - 流程图、Ribbon Bar功能升级
BCGControlBar库拥有500多个经过全面设计、测试和充分记录的MFC扩展类。 我们的组件可以轻松地集成到您的应用程序中,并为您节省数百个开发和调试时间。 BCGControlBar专业版 v33.6已正式发布了,此版本包含了对图表组件的改进、带隐藏标签的单类功能区栏…...

前端 JS 经典:文件流下载
重点:调用接口时,一定要配置 responseType 的值为 blob,不然获取的文件流,不会转义成 blob 类型的文件。 1. 接口返回文件流 // BLOB (binary large object)----二进制大对象,是一个可以存储二进制文件的容器 // 下载…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
