golang:context
context作用
goroutine的退出机制
多个goroutine都是平行的被调度的,多个goroutine如何协调工作涉及通信、同步、通知和退出
-
通信:goroutine之间的通信同步chan通道
-
同步:不带缓冲的chan提供了一个天然的同步等待机制。通过WaitGroup也可以为多个goroutine提供同步等待机制
-
通知:这个通知和上面通信的数据不一样,通知通常不是业务数据,而是管理、控制流数据。要处理这个也好办,在输入端绑定两个chan,一个用于业务流数据,另一个用于异常通知数据,然后通过 select 收敛进行处理。这个方案可以解决简的问题,但不是一个通用的解决方案。
-
退出:goroutine 之间没有父子关系,如何通知 goroutine 退出?可以通过增加一个个单独的通道,借助通道和 select 的广播机制( close channel to broadcast)实现退出
通知退出机制:
-
读取已经关闭的通道不会引起阻塞,也不会导致panic,而是立即返回该通道存储类型的零值
-
关闭select监听的某个通道能使select立即感知这种通知,然后进行相应的处理,即所谓的退出通知机制
contet库的设计目的就是跟踪 goroutine调用树,并在这些goroutine 调用树中递通知和元数据
-
退出通知机制:通知可以传递给整个 goroutine调用树上的每一个goroutine
-
传递数据:数据可传递给整个goroutine 调用树上的每一个goroutine
使用
var wg sync.WaitGroup
func main() {background := context.Background()//通过cancel进行控制/*cancelctx, cancelFunc := context.WithCancel(background)wg.Add(2)go jiankong1(cancelctx)time.Sleep(time.Second * 2)println("并不是因为主协程退出,而导致另一个协程退出,而是通过cancel方法通知另一个协程进行退出!")cancelFunc()wg.Wait()println("完成退出")*///通过deadline进行控制,也可以通过返回的cancelFunc手动进行控制/*deadline, _ := context.WithDeadline(background, time.Now().Add(time.Second*2))go deadF(deadline)time.Sleep(time.Second * 4)println("结束")*///通过timeout控制,也可以通过返回的cancelFunc手动进行控制 超时以后报的错和deadline控制方式一样 context deadline exceededtimeout, _ := context.WithTimeout(background, time.Second*2)go deadF(timeout)time.Sleep(time.Second * 4)println("结束")
}func deadF(ctx context.Context) {for true {select {case <-ctx.Done():fmt.Println("只给了两秒的执行时间,时间到了,我得退出了。")//此处打印的错误为 context deadline exceededprintln(ctx.Err().Error())returndefault:time.Sleep(time.Millisecond * 1000)fmt.Println("我正在执行...")}}
}func jiankong1(ctx context.Context) {defer wg.Done()cancel, _ := context.WithCancel(ctx)go jiankong2(cancel)for true {select {case <-ctx.Done():fmt.Println("别人通知我主动退出了。在此处进行收尾工作,释放资源等")//此处报错为:context canceledfmt.Println(ctx.Err().Error())returndefault:time.Sleep(time.Millisecond * 100)fmt.Println("我在持续监控中...")}}
}func jiankong2(ctx context.Context) {defer wg.Done()for true {select {case <-ctx.Done():fmt.Println("上级通知我主动退出了。")fmt.Println(ctx.Err().Error())returndefault:time.Sleep(time.Millisecond * 100)fmt.Println("me在持续监控中...")}}
}Tips:
异步任务使用context注意点:
使用go func进行异步任务传入context时,要考虑context的过期时间,如果异步任务不考虑过期时间,则最好传入一个无过期时间的context,负责异步任务多或执行时间长context会过期,影响异步任务的执行。
场景:mongo批量插入数据后,将返回的Id集合传入异步任务(在异步任务中通过id查询数据),如果共用了接口设置过期时间的context,可能会导致一部分数据查询不到(context过期导致)
相关文章:

golang:context
context作用 goroutine的退出机制 多个goroutine都是平行的被调度的,多个goroutine如何协调工作涉及通信、同步、通知和退出 通信:goroutine之间的通信同步chan通道 同步:不带缓冲的chan提供了一个天然的同步等待机制。通过WaitGroup也可以…...

探讨代理IP与Socks5代理在跨界电商中的网络安全应用
在数字化时代,跨界电商已经成为了商业世界中的一大趋势。然而,跨越国界的电商活动也伴随着网络安全挑战。本文将讨论如何利用代理IP和Socks5代理技术来提高跨界电商中的网络安全,同时也探讨了与游戏相关的爬虫应用。 1. 代理IP和Socks5代理的…...
Guava Cache介绍-面试用
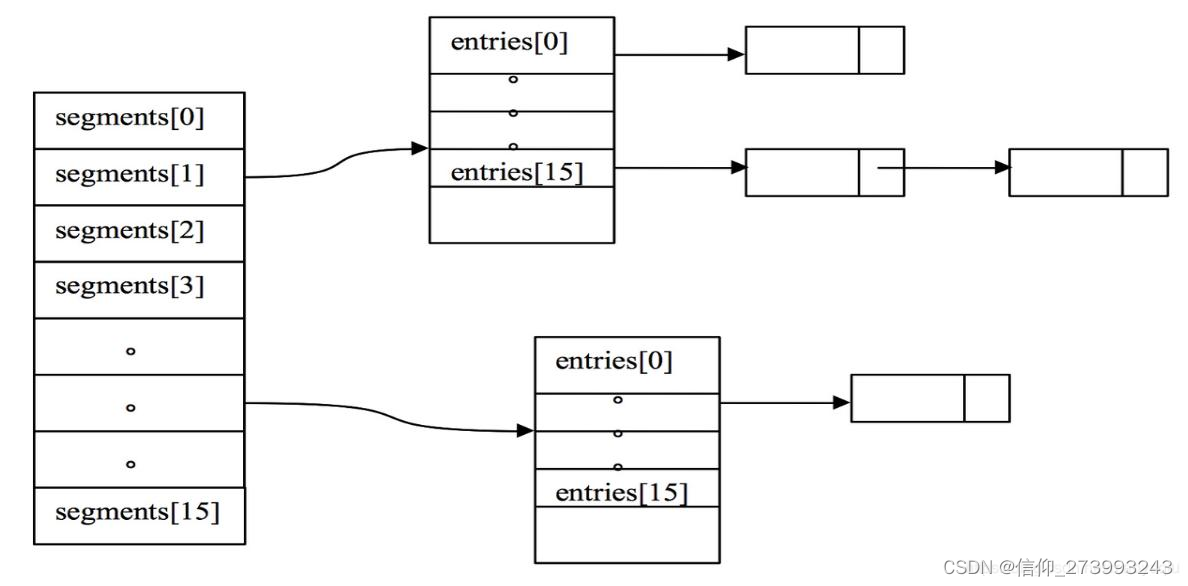
一、Guava Cache简介 1、简介 Guava Cache是本地缓存,数据读写都在一个进程内,相对于分布式缓存redis,不需要网络传输的过程,访问速度很快,同时也受到 JVM 内存的制约,无法在数据量较多的场景下使用。 基…...

ARM 汇编指令作业(求公约数、for循环实现1-100之间和、从SVC模式切换到user模式简单写法)
1、求两个数最大公约数 .text .globl _start_start:mov r0, #9mov r1, #15 Loop: 循环cmp r0,r1 比较r0和r1的大小beq stop 当r0和r1相等时,跳到stop标签subhi r0,r0,r1 r0-r1>0 时,证明r0>r1,将r0-r1的值赋给r0&…...

Go - 【字符串,数组,哈希表】常用操作
一. 字符串 字符串长度: s : "hello" l : len(s) fmt.Println(l) // 输出 5遍历字符串: s : "hello" for i, c : range s {fmt.Printf("%d:%c ", i, c) } // 输出:0:h 1:e 2:l 3:l 4:ofor i : 0; i < le…...

vue 普通组件的 局部注册
vue 普通组件的 注册 11 Vue2_3入门到实战-配套资料\01-随堂代码素材\day03\素材\00-准备代码\小兔鲜首页静态页\src...
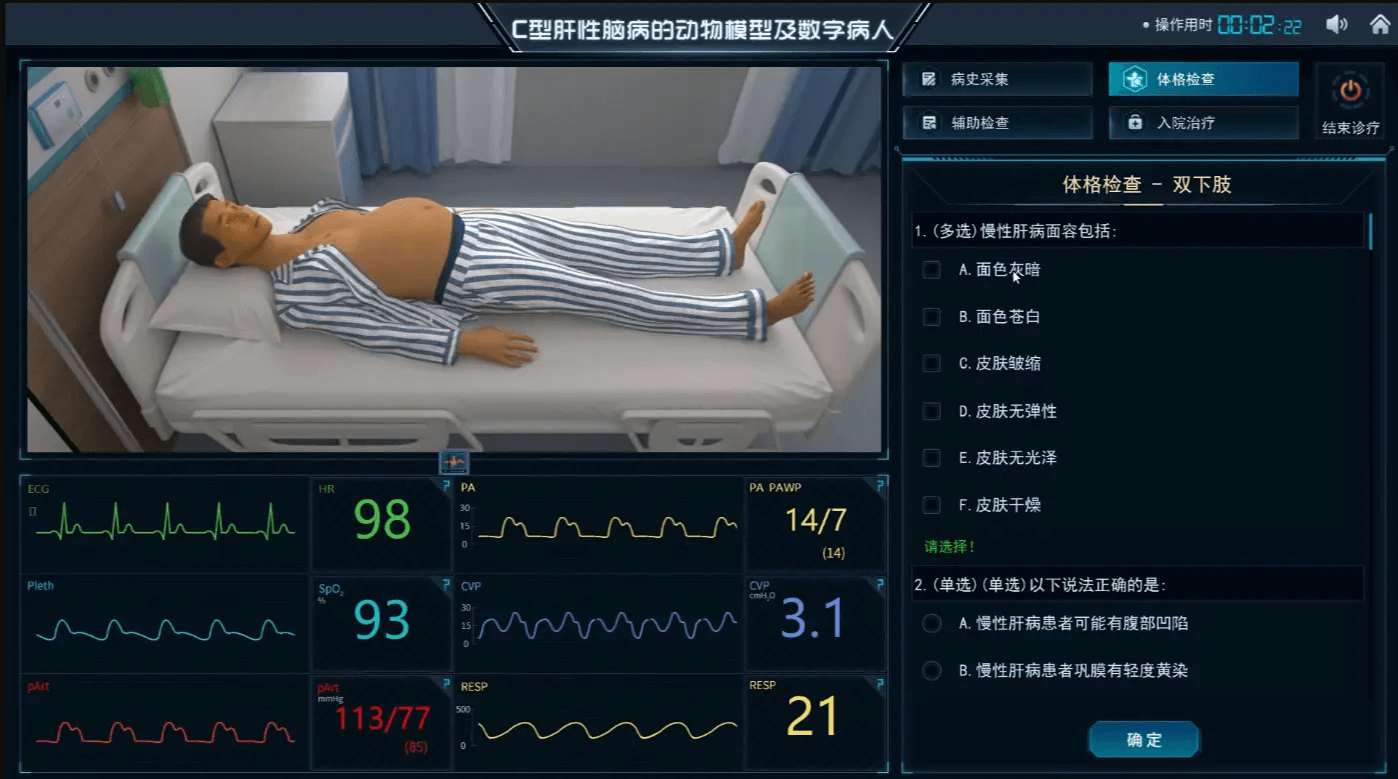
医疗虚拟仿真和虚拟现实有什么区别?哪个更好?
随着我们在仿真教育中越来越多地使用新技术,区分虚拟模式的类型很重要。虚拟仿真是一个统称,用来概括术语来描述各种基于仿真的体验,从基于屏幕的平台到沉浸式虚拟现实。然而,各虚拟平台在保真度、沉浸感和临场感的水平上有很大差…...

【.net core】yisha框架使用nginx代理swagger接口无法访问问题
后端代码配置 #在StartUp.cs文件中Configure方法中增加以下代码 app.UseSwagger(c >{//代理路径访问c.PreSerializeFilters.Add((doc, item) >{//根据代理服务器提供的协议、地址和路由,生成api文档服务地址doc.Servers new List<OpenApiServer>{ new…...

uniapp录音功能和音频播放功能制作
录音功能 在 UniApp 中,你可以使用 uni.getRecorderManager() 方法来创建一个录音管理器实例,从而实现录音功能。 以下是一个示例,演示了如何在 UniApp 中使用 uni.getRecorderManager() 实现录音功能: // 在需要录音的页面或组…...

服务器数据恢复-LINUX操作系统下各文件系统误删除/格式化数据的恢复方案
服务器数据恢复环境: 基于EXT2/EXT3/EXT4/Reiserfs/Xfs文件系统的Linux操作系统。 服务器故障: LINUX操作系统下误删除/格式化数据。 服务器数据恢复过程: 1、首先会检测服务器是否存在硬件故障,如果检测出硬件故障,交…...
 、upper_bound,bisect_left,bisect_right))
python/C++二分查找库函数(lower_bound() 、upper_bound,bisect_left,bisect_right)
二分查找是一种经典的搜索算法,广泛应用于有序数据集中。它允许在大型数据集中高效地查找目标元素,减少了搜索的时间复杂度。本文将介绍在 C 和 Python 中内置的二分查找函数,让二分查找变得更加容易。 c lower_bound() 、upper_bound 定义…...

爬虫 — App 爬虫(二)
目录 一、Appium介绍二、node.js 安装三、Java 的 SDK 安装以及配置1、安装步骤2、配置环境变量 四、安卓环境的配置1、配置环境变量 五、Appium 安装1、安装2、打开 APP3、使用 六、Appium 使用1、定位数据(方法一,不常用)2、定位数据&#…...
汽车电子相关术语
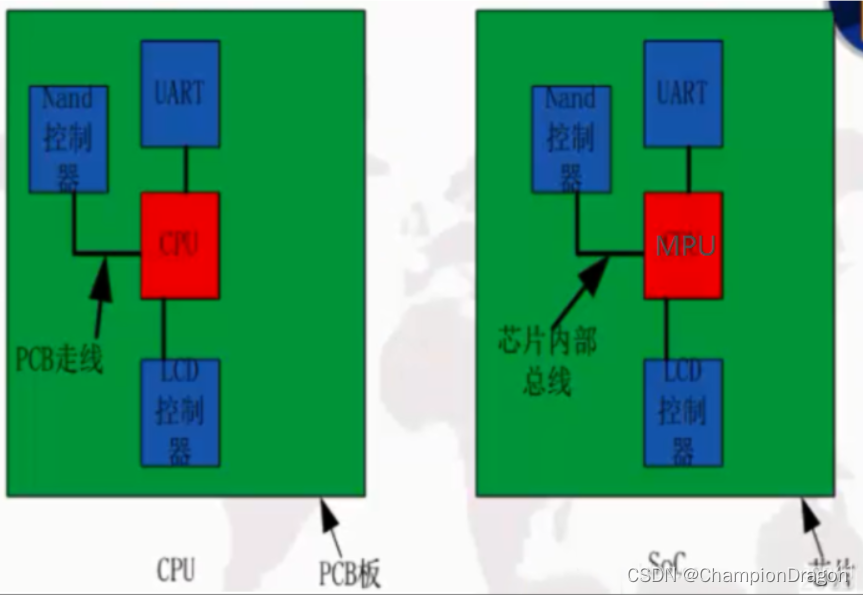
SOA SOA(Service-Oriented Architecture,面向服务的架构)是一种在计算机环境中设计、开发、部署和管理离散模型的方法。是由Garnter1996年提出的概念,将应用程序的不同功能单元(称为服务)进行拆分…...
Python 找出最大数
"""在输入的三个数中找出最大知识点:1、条件嵌套语句if/else2.字符串分割函数split()3、列表元素索引4、数据类型转换举一反三:1、如何控制只能输入三个数,否则重新输入2、如何避免输入无效字母"""# 定义一个变…...

Spring Security 用了那么久,你对它有整体把控吗?
文章目录 1.Servlet Filter:守门人的角色2.DelegatingFilterProxy:桥接 Servlet 和 Spring 的神器3.FilterChainProxy:Spring Security 过滤器链的管家3.SecurityFilterChain:Security 过滤器的串绳4.Spring Security 中的过滤器机…...

vue+minio实现文件上传操作
vueminio实现文件上传操作 minio文件上传vueminio实现文件上传操作 minio文件上传 minio文件上传有两种方法: 第一种是通过ak,sk,调用minio的sdk putObject进行文件上传;该方法支持go,java,js等各种语言&…...

使用JavaScript实现无限滚动的方法
前言 在网页设计中,无限滚动是一种常见的交互方式,用户可持续地加载更多内容而无需刷新页面,提高用户体验。本文将介绍如何运用JavaScript实现无限滚动的效果,使网页能够自动加载更多数据,减轻用户加载新页的负担&…...
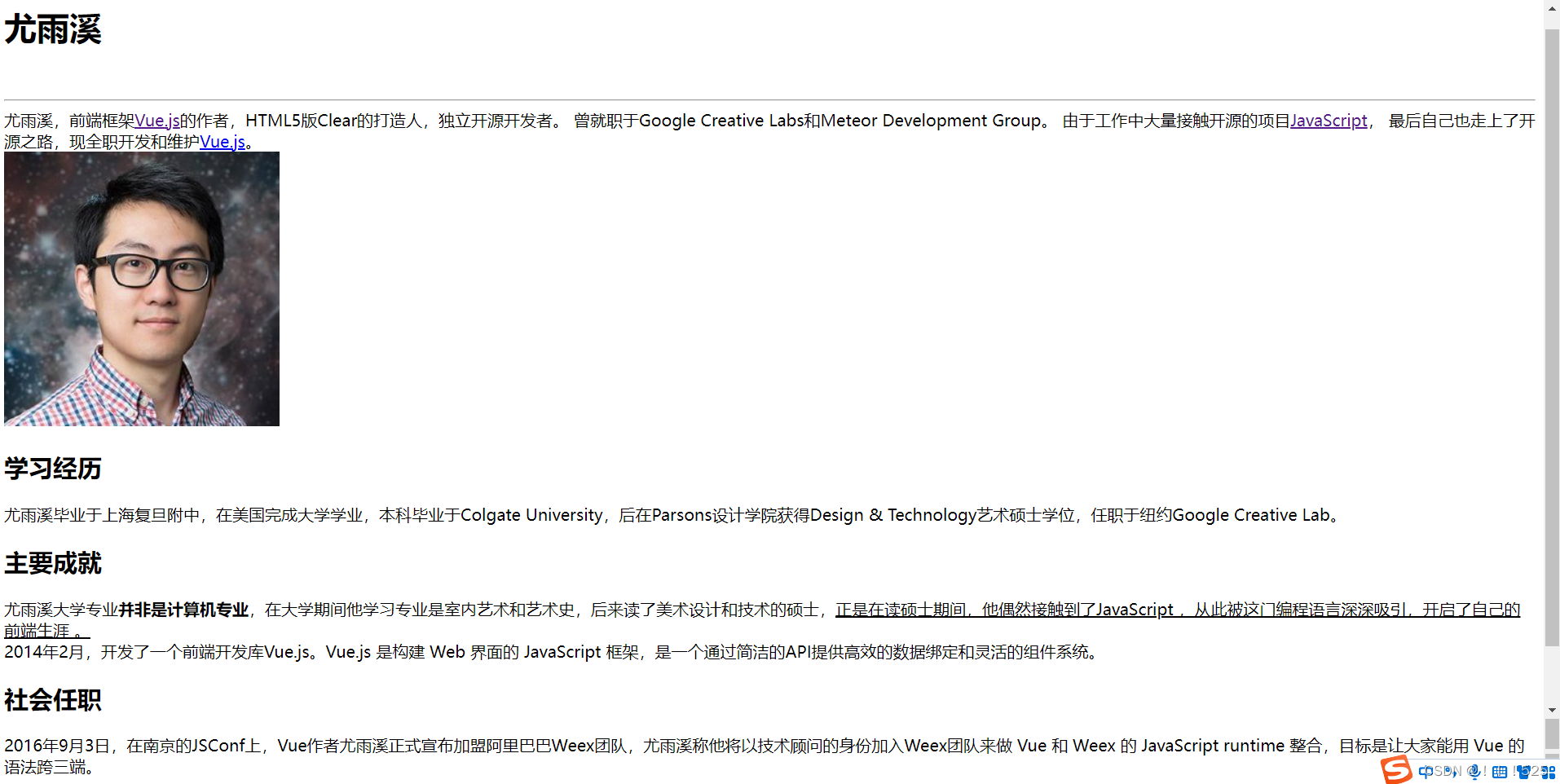
html学习综合案例1
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>个人简介</title> </head> <body>…...

神经节苷脂抗体——博迈伦
神经节苷脂抗体是指人体免疫系统中产生的一类抗体,其主要作用是攻击神经节苷脂抗原物质。神经节苷脂是一种存在于神经细胞表面的重要分子,参与了神经细胞间的信号传导和细胞黏附等重要功能。正常情况下,人体免疫系统不会对神经节苷脂产生抗体…...
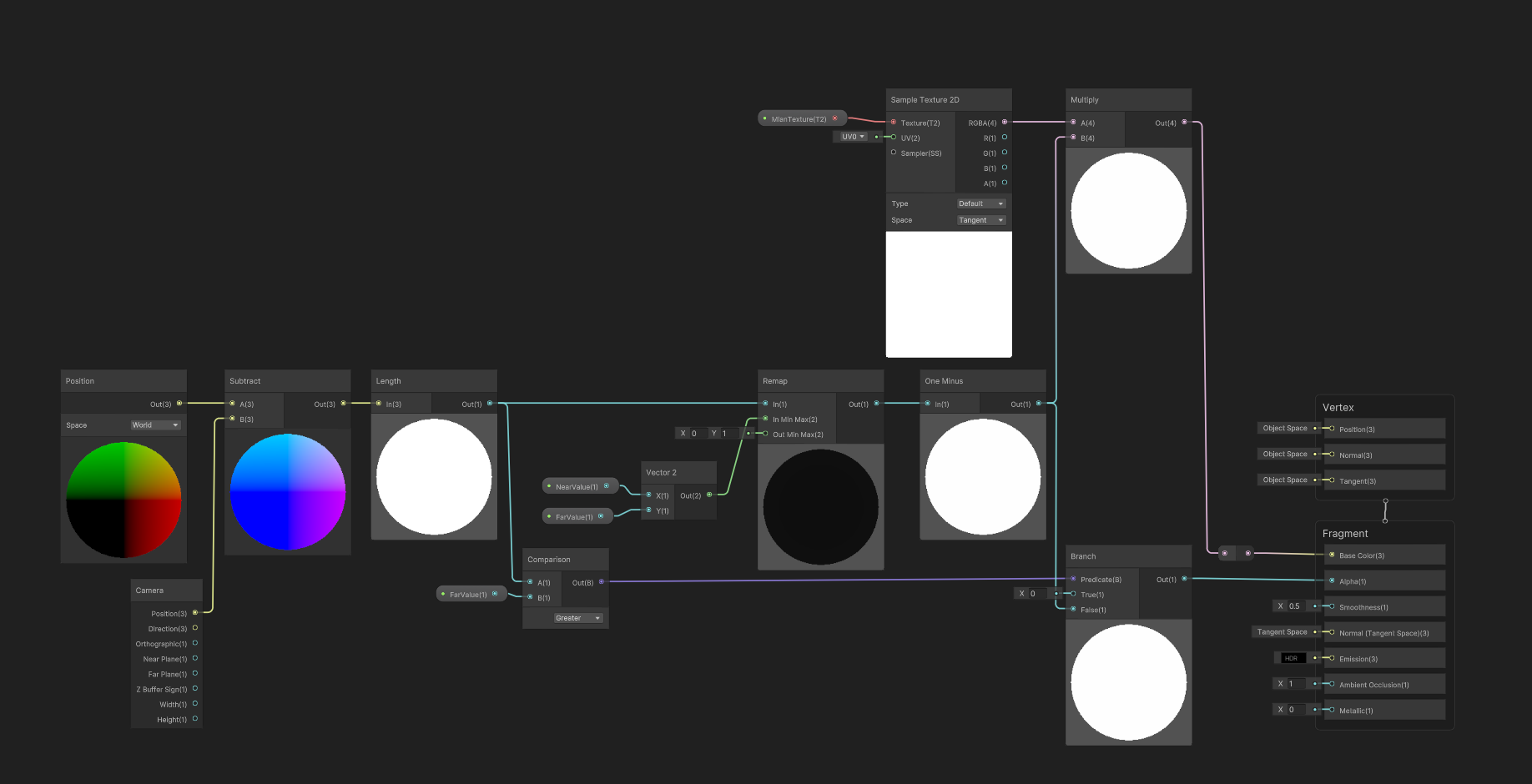
【Unity】简单的深度虚化shader
【Unity】简单的深度虚化shader 实现效果 可以用于对地图场景边界的白模处理 实现方法 1.关键方法 UnityObjectToClipPos:将物体坐标转换为屏幕坐标 LinearEyeDepth:将屏幕坐标中的z值转换为实际的深度值 saturate:将值规范到0~1之间&a…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
