红 黑 树
文章目录
- 一、红黑树的概念
- 二、红黑树的实现
- 1. 红黑树的存储结构
- 2. 红黑树的插入
一、红黑树的概念
在 AVL 树中删除一个结点,旋转可能要持续到根结点,此时效率较低
红黑树也是一种二叉搜索树,通过在每个结点中增加一个位置来存储红色或黑色,并对结点的着色进行限制,使得该二叉搜索树的最长路径不超过最短路径的两倍,即红黑树是一颗近似平衡的二叉搜索树,他不像 AVL 树的平衡那么严格,所以红黑树在插入和删除时,也不需要大量的旋转,并且搜索效率差不了 AVL 多少
红黑树是一颗二叉搜索树并且满足如下规则:
- 每个节点不是红色就是黑色
- 根结点是黑色的
- 每个红结点的左右孩子一定是黑色
- 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点
- 叶结点都是黑色的(这里的叶结点指的是空节点)
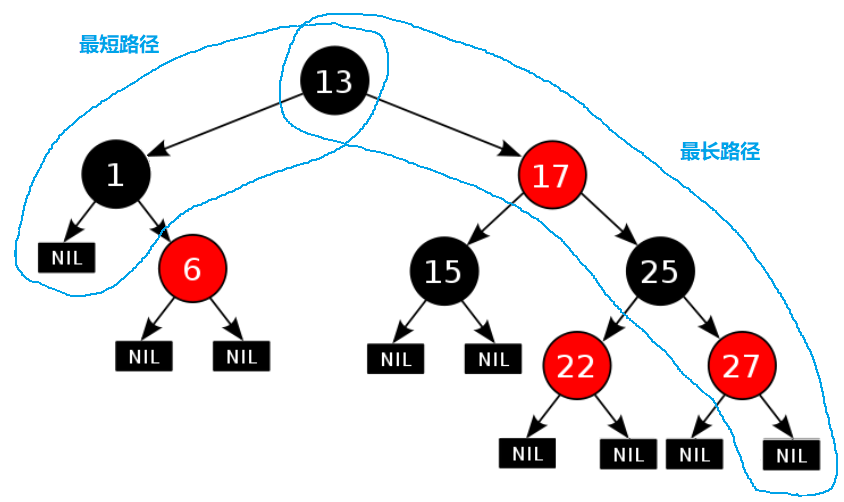
根据上述规则可以得到:最短路径:全黑结点的路径,最长路径:一黑一红的路径,所以红黑树可以保证最长路径不超过最短路径的一半
二、红黑树的实现
1. 红黑树的存储结构
// 结点的颜色
enum Color { RED, BLACK };// 红黑树的结点
template<class K, class V>
struct RBTreeNode
{std::pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _color; // 结点的颜色RBTreeNode<K, V>(const std::pair<K, V>& kv = std::pair<K, V>(K(), V())): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _color(RED) // 为了方便树的结构调整,新结点默认为红色{}
};// 红黑树
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:RBTree<K, V>(): _root(nullptr){}private:Node* _root;
};
2. 红黑树的插入
首先按照二叉搜索树的方式插入结点,保证插入结点之后还是二叉搜索树,为了方便树的结构调整,插入结点默认为为红色,当插入结点完成之后,可能会违反红黑树的性质,此时有三种情况
-
插入结点的父节点是黑色:没有违反红黑树的性质
-
插入结点的父节点是红色,叔节点存在且为红:违反了红黑树的性质,此时需要对父节点和爷爷结点进行变色
由于父节点是红色的,所以爷爷结点一定存在且为黑,变色完之后,如果 g 结点是根结点,则将 g 结点变为黑色,否则将 g 结点所在的子树当做新插入的结点,继续向上调整

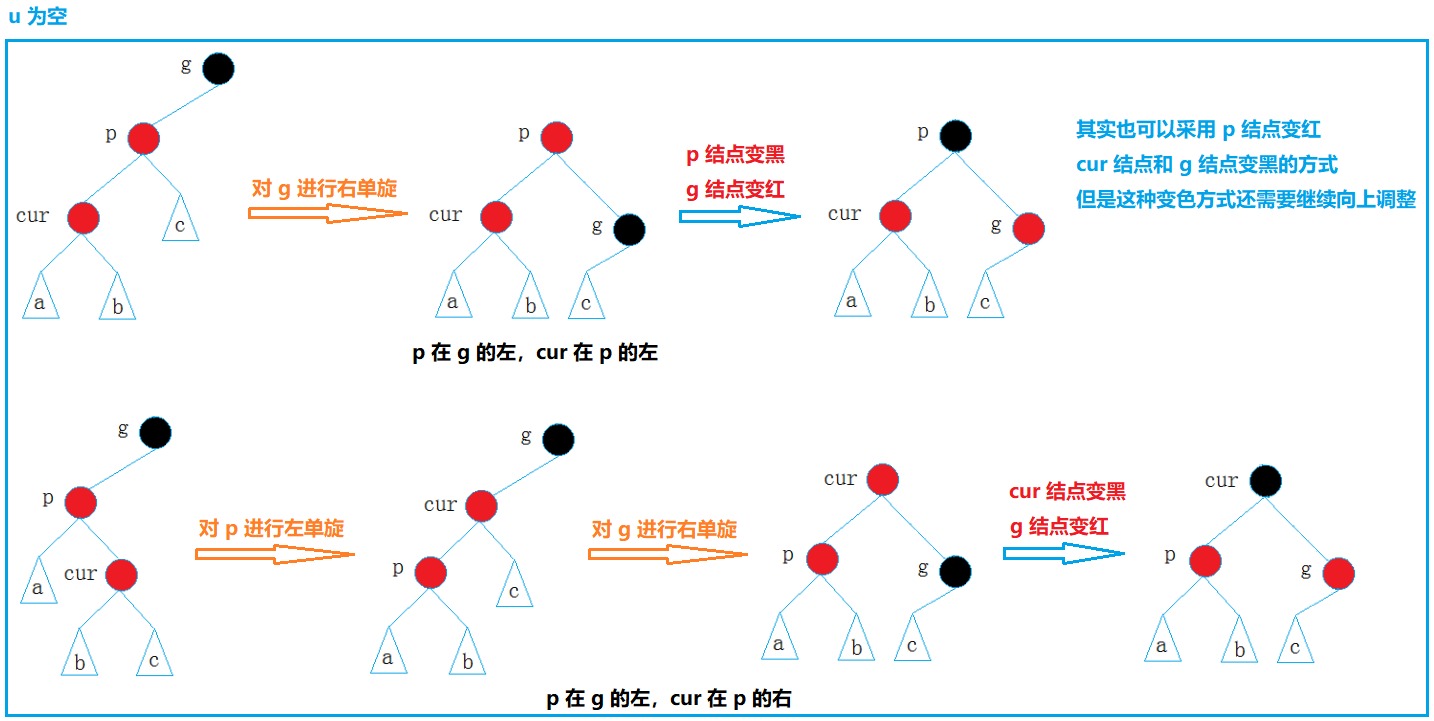
- 插入结点的父节点是红色,叔节点不存在或存在且为黑:违反了红黑树的性质,此时需要对爷爷结点所在的子树进行旋转然后再对结点进行变色
由于父节点是红色的,所以爷爷结点一定存在且为黑,变色完之后,子树的根结点是黑色的,不用继续向上调整
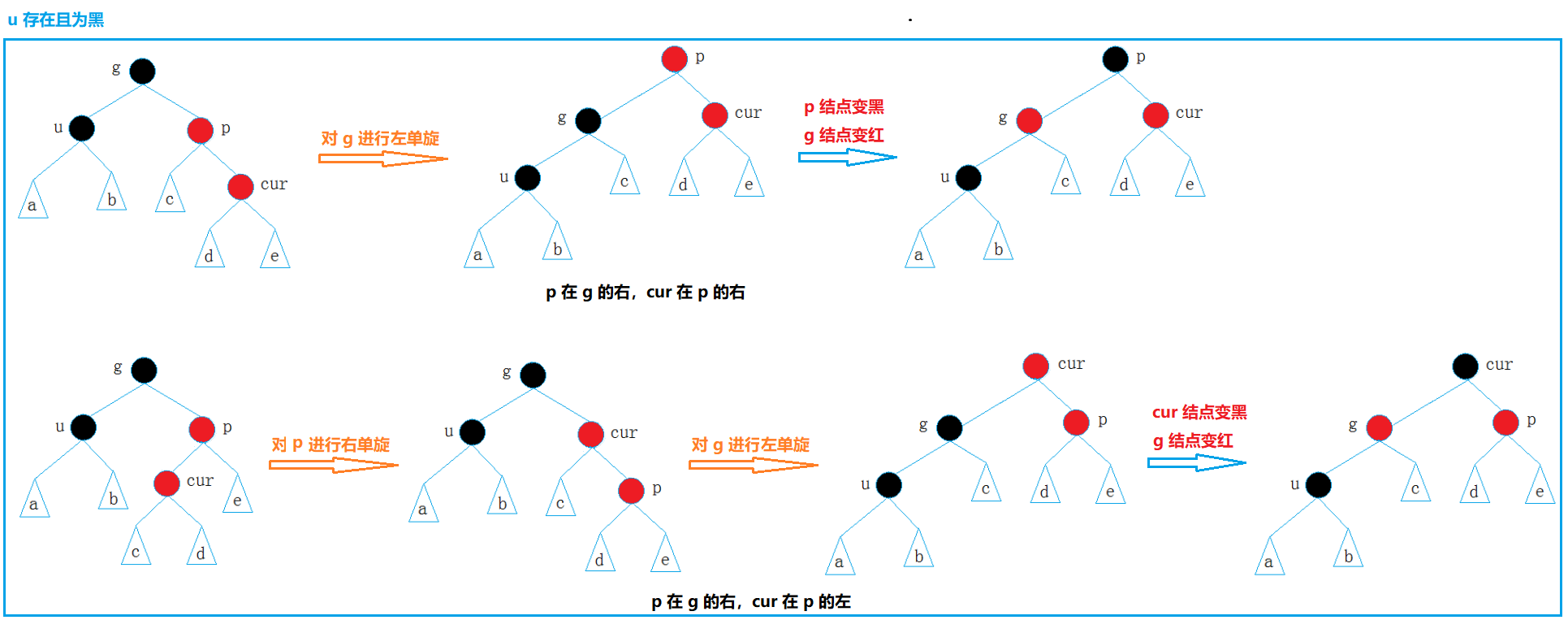
u 存在且为黑的情况,一定是由 u 存在且为红的情况继续向上调整而来的
// 右旋
void RotateR(Node* parent)
{Node* pparent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr) _root = subL;else{if (pparent->_left == parent) pparent->_left = subL;else pparent->_right = subL;}subL->_parent = pparent;
}// 左旋
void RotateL(Node* parent)
{Node* pparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (pparent == nullptr) _root = subR;else{if (pparent->_left == parent) pparent->_left = subR;else pparent->_right = subR;}subR->_parent = pparent;
}// 插入
bool Insert(const std::pair<K, V>& kv)
{// 按照二叉搜索树的方式插入结点,保证该树插入结点之后还是二叉搜索树if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else return false;}cur = new Node(kv);if (parent->_kv.first > kv.first) parent->_left = cur;else parent->_right = cur;cur->_parent = parent;// 更新颜色while (parent && parent->_color == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// u 存在且为红// u 不存在或存在且为黑// p 为 g 的左,cur 为 p 的左 右单旋// p 为 g 的左,cur 为 p 的右 先左旋再右旋if (uncle && uncle->_color == RED){grandfather->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;// 继续判断是否违反了红黑树的性质cur = grandfather;parent = grandfather->_parent;}else{if (parent->_left == cur){RotateR(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{RotateL(parent);RotateR(grandfather);grandfather->_color = RED;cur->_color = BLACK;}}}else{Node* uncle = grandfather->_left;// u 存在且为红// u 不存在或存在且为黑// p 为 g 的右,cur 为 p 的右 左单旋// p 为 g 的右,cur 为 p 的左 先右旋再左旋if (uncle && uncle->_color == RED){grandfather->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;// 继续判断是否违反了红黑树的性质cur = grandfather;parent = grandfather->_parent;}else{if (parent->_right == cur){RotateL(grandfather);grandfather->_color = RED;parent->_color = BLACK;}else{RotateR(parent);RotateL(grandfather);grandfather->_color = RED;cur->_color = BLACK;}}}}_root->_color = BLACK;return true;
}
相关文章:

红 黑 树
文章目录 一、红黑树的概念二、红黑树的实现1. 红黑树的存储结构2. 红黑树的插入 一、红黑树的概念 在 AVL 树中删除一个结点,旋转可能要持续到根结点,此时效率较低 红黑树也是一种二叉搜索树,通过在每个结点中增加一个位置来存储红色或黑色…...
)
掷骰子的多线程应用程序1(复现《Qt C++6.0》)
说明:复现的代码来自《Qt C6.0》P496-P500。在复现时完全按照代码,出现了两处报错: (1)ui指针(2)按钮的响应函数。下面程序对以上问题进行了修改。除了图片、清空、关闭功能外,其他…...

【vue2第十八章】VueRouter 路由嵌套 与 keep-alive缓存组件(activated,deactivated)
VueRouter 路由嵌套 在使用vue开发中,可能会碰到使用多层级别的路由。比如: 其中就包含了两个主要页面,首页,详情,但是首页的下面又包含了列表,喜欢,收藏,我的四个子路由。 此时就…...

如何确保亚马逊、速卖通等平台测评补单的环境稳定性和安全性?
做亚马逊、速卖通等平台测评补单时,确保环境的安全性和稳定性是非常重要的。稳定的环境是测评的基础,如果无法解决安全性问题,那么测评就不值得进行。为了确保稳定的环境系统,需要考虑物理环境和IP环境两个方面。 首先࿰…...
echarts图表 实现高度按照 内容撑起来或者超出部分滚动展示效果
背景:因为数据不固定 高度写死导致数据显示不全,所以图表高度要根据内容计算 实现代码如下: <divv-if"showCharts"id"business-bars"class"chart":style"{ height: chartHeight px }"></d…...

【论文阅读】检索增强发展历程及相关文章总结
文章目录 前言Knn-LMInsightMethodResultsDomain AdaptionTuning Nearest Neighbor Search Analysis REALMInsightsMethodKnowledge RetrieverKnowledge-Augmented Encoder ExpResultAblation StudyCase Study DPRInsightMethodExperimentsResults RAGInsightRAG-Sequence Mode…...
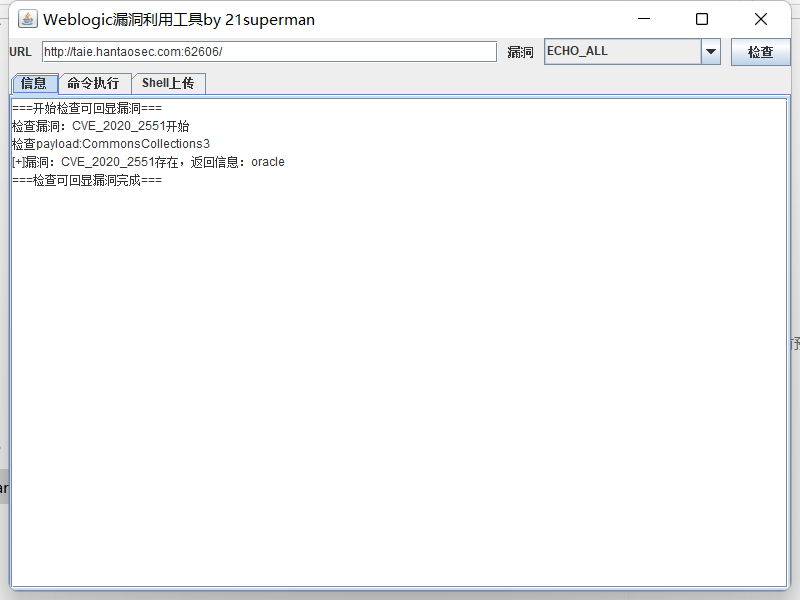
【漏洞复现系列】二、weblogic-cve_2020_2883(RCE/反序列化)
Key words:T3协议,weblogic Server,反序列化 2.1、漏洞原理 cve_2020_2883 远程代码执行漏洞存在于 WebLogic Server 核心组件中,允许未经身份验证的攻击者通过 T3 协议网络访问并破坏易受攻击的 WebLogic Server,成功的漏洞利…...

算法通关村-----LRU的设计与实现
LRU 缓存 问题描述 请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存。int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值&…...
王江涛十天搞定考研词汇
学习目标: 考研词汇 学习内容: 2023-9-17 第一天考研词汇 学习时间: 开始:2023-9-17 结束:进行中 学习产出: 2023-9-17intellect智力;知识分子intellectual智力的;聪明的intellectualize使...理智化&a…...
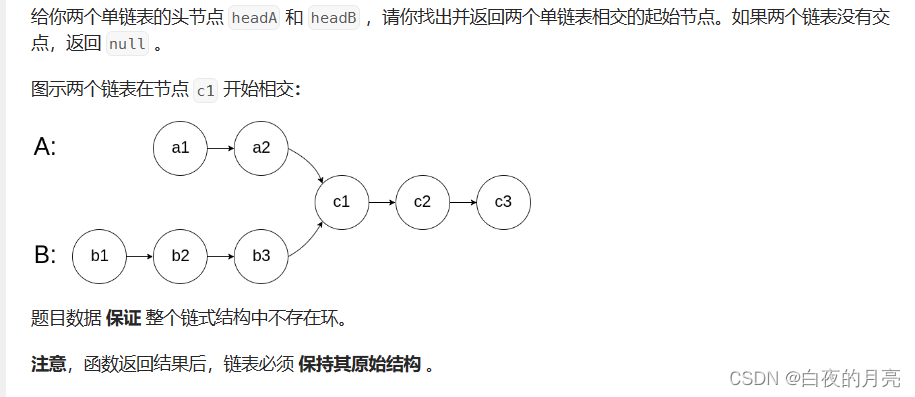
算法(二)——数组章节和链表章节
数组章节 (1)二分查找 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 class Solution {public i…...
Android:ListView在Fragment中的使用
一、前言: 因为工作一直在用mvvm框架,因此这篇文章是基于mvvm框架写的。在Fragment复制之前一定要谨记项目可以跑起来。确保能跑起来之后直接复制就行。 二、代码展示: 页面布局 ?xml version"1.0" encoding"utf-8"…...
BIGEMAP在土地规划中的应用
工具 Bigemap gis office地图软件 BIGEMAP GIS Office-全能版 Bigemap APP_卫星地图APP_高清卫星地图APP 1.使用软件一般都用于套坐标,比如我们常见的(kml shp CAD等土建规划图纸)以及一些项目厂区红线,方便于项目选址和居民建…...

软件测试常见术语和名词解释
1. Unit testing (单元测试):指一段代码的基本测试,其实际大小是未定的,通常是一个函数或子程序,一般由开发者执行。 2. Integration testing (集成测试):被测试系统的所有组件都集成在一起,找出被测试系统…...

prometheus+process_exporter进程监控
一、需要监控进程的服务器上配置 1、进入到临时工作目录,传入process_exporter包 [root Nginx1 ~]# cd work/ [root Nginx1 work]# rz 2、解压,并移动至/usr/local/目录下 [root Nginx1 work]# tar xzf process-exporter-0.7.5.linux-amd64.tar.gz [root…...

四川玖璨电子商务有限公司专注抖音电商运营
四川玖璨电商是一个靠谱的抖音培训公司,在电商行业内有着广泛的知名度和良好的口碑。该公司通过多年的发展,形成了独特的运营理念和有效的运营策略,为商家提供了一站式的抖音电商运营服务。 首先,四川玖璨电子商务有限公司注重与…...

python LeetCode 刷题记录 83
题目 给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。 代码 class Solution:def deleteDuplicates(self, head: Optional[ListNode]) -> Optional[ListNode]:if head:# 判断非空链表current he…...

Grom 如何解决 SQL 注入问题
什么是 SQL 注入 SQL 注入是一种常见的数据库攻击手段, SQL 注入漏洞也是网络世界中最普遍的漏洞之一。 SQL 注入就是恶意用户通过在表单中填写包含 SQL 关键字的数据来使数据库执行非常规代码的过程。 这个问题的来源就是, SQL 数据库的操作是通过 SQ…...
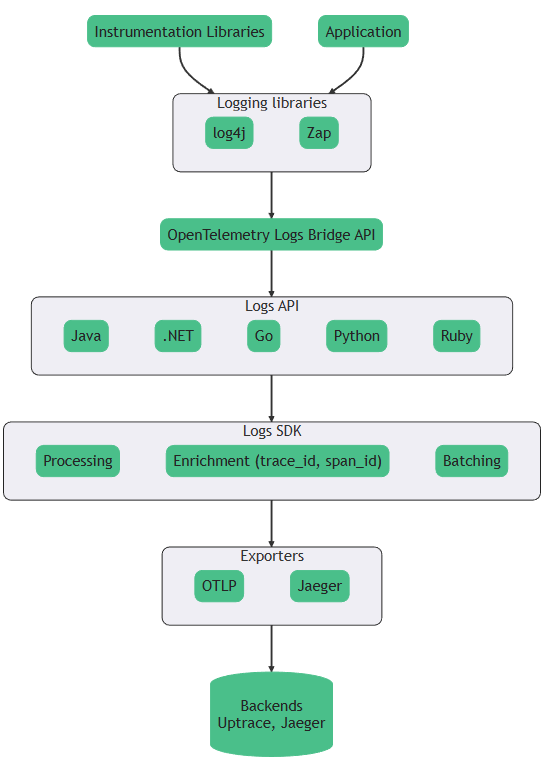
腾讯mini项目-【指标监控服务重构】2023-07-19
今日已办 OpenTelemetry Logs 通过日志记录 API 支持日志收集 集成现有的日志记录库和日志收集工具 Overview 日志记录 API - Logging API,允许您检测应用程序并生成结构化日志旨在与其他 telemerty data(例如metric和trace)配合使用&am…...
抖音矩阵系统源代码开发部署--SaaS开源技术开发文档
一、概述 抖音SEO矩阵系统源代码是一套针对抖音平台的搜索引擎优化工具,它可以帮助用户提高抖音视频在搜索结果中的排名,增加曝光率和流量。本开发文档旨在提供系统的功能框架、技术要求和开发示例,以便开发者进行二次开发和优化。 二、功能…...

CLIP模型资料学习
clip资料 links https://blog.csdn.net/wzk4869/article/details/129680734?ops_request_misc&request_id&biz_id102&utm_termCLIP&utm_mediumdistribute.pc_search_result.none-task-blog-2allsobaiduweb~default-4-129680734.142v94insert_down1&spm10…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
