【简单的自动曝光】python实现-附ChatGPT解析
1.题目
一个图像有
n个像素点，存储在一个长度为n的数组img里，
每个像素点的取值范围[0,255] 的正整数。
请你给图像每个像素点值,加上一个整数k(可以是负数)，得到新图newImg，
使得新图newImg的所有像素平均值最接近中位值128。
请输出这个整数k。
输入描述
n 个整数，中间用空格分开，例如:
0 0 0 0
4 个数值，中间用空格分开
输出描述
一个整数k
备注:
1、1 <= n <= 100
2、如有多个整数 k 都满足，输出小的那个 k;
3、新图的像素值会自动截取到[0,255]范围。
当新像素值<0，其值会更改为0；
当新像素值>255，其值会更改为255;
例如newImg=“-1 -2 256”,会自动更改为“0 0 255”.
示例1
输入:
000o
输出:
128
说明: 四个像素值都为0
示例2
输入:
129 130 129 130
输出:
-2
相关文章：
【简单的自动曝光】python实现-附ChatGPT解析
1.题目 一个图像有 n 个像素点，存储在一个长度为 n 的数组 img 里， 每个像素点的取值范围[0,255] 的正整数。 请你给图像每个像素点值,加上一个整数 k (可以是负数)，得到新图 newImg ， 使得新图newImg 的所有像素平均值最接近中位值 128。 请输出这个整数 k。 输入描述 n …...
网工内推 | 运维工程师，CCNP认证优先，周末双休，多次调薪机会
01 驻场运维 职责描述： 1、驻场某大型汽车整车厂，配合客户完成网络相关（路由交换）的项目。 2、按照客户要求，与项目组配合共同完成项目前期调研，设计，规划，项目中期调试测试&#…...
LeetCode 1337. The K Weakest Rows in a Matrix【数组,二分,堆,快速选择,排序】1224
本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章…...
如何使用Spring提供的Retry
0、本例中使用的是 springboot-2.0.4.RELEASE，jdk1.8 1、导包。需要注意版本。2.0.0需要spring6和jdk17 <dependency><groupId>org.springframework.retry</groupId><artifactId>spring-retry</artifactId><version>1.3.4<…...
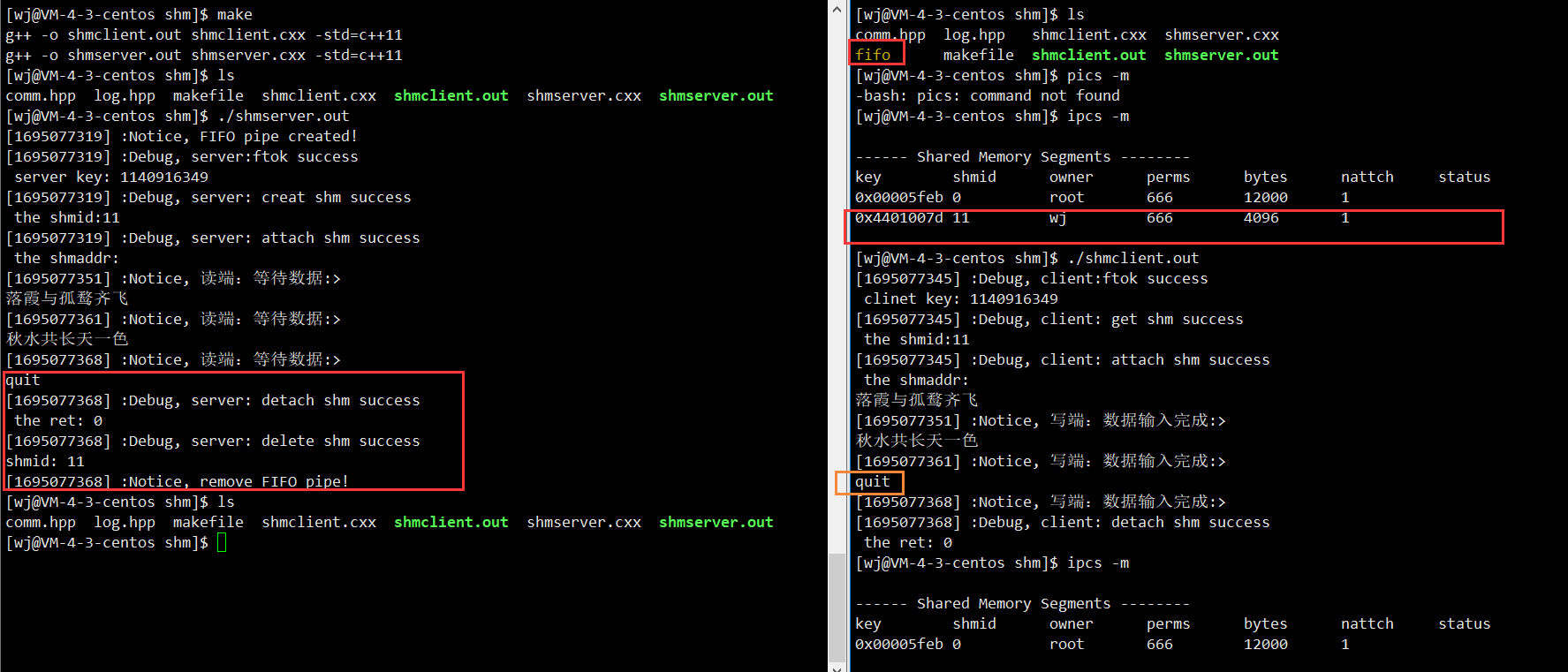
【ONE·Linux || 进程间通信】
总言 进程间通信：简述进程间通信，介绍一些通信方式，管道通信（匿名、名命）、共享内存等。 文章目录 总言1、进程间通信简述2、管道2.1、简介2.2、匿名管道2.2.1、匿名管道的原理2.2.2、编码理解：用fork来共…...
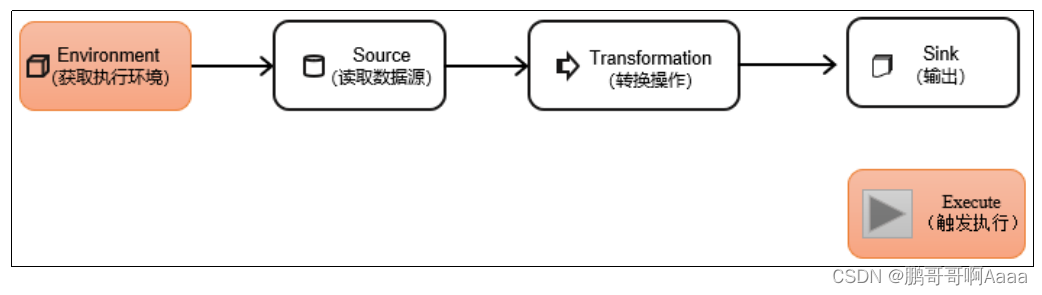
207.Flink（二）：架构及核心概念，flink从各种数据源读取数据，各种算子转化数据，将数据推送到各数据源
一、Flink架构及核心概念 1.系统架构 JobMaster是JobManager中最核心的组件，负责处理单独的作业（Job）。一个job对应一个jobManager 2.并行度 （1）并行度（Parallelism）概念 一个特定算子的子任务（subtask）的个数被称之为其并行度（parallelism）。这样，包含并行子任…...
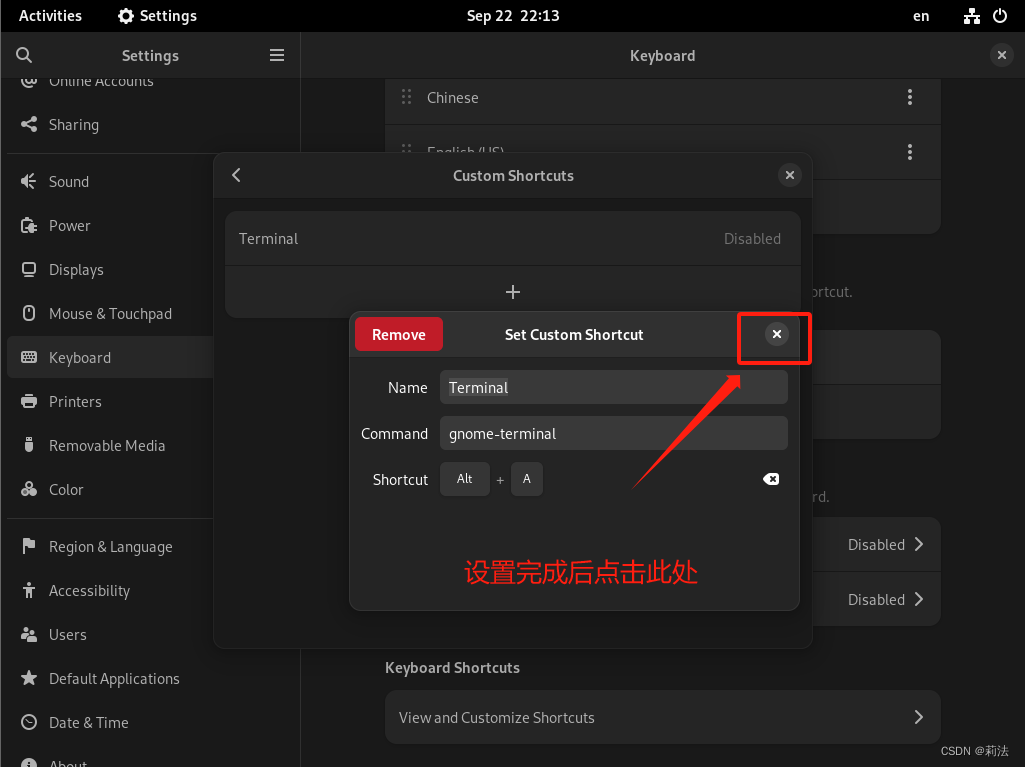
debian终端快捷键设置
为了方便使用图形化debian，快捷调出shell终端是提升工作学习效率的最重要的一步。 1.首先点击右上角，选择设置 2.点击键盘，选择快捷键，并创建自定义快捷键 3.点击添加快捷键 4.根据图中提示创建快捷键 Name: Terminal Command…...
原生ajax
什么是Ajax Asynchronous JavaScript and xml 异步的 js 和 xml(数据承载方式) ，本质：使用js提供的异步对象XMLHttpRequest 异步的向服务器提交请求，并且接受服务器响应回来的数据。 使用ajax 1.创建异步对象 var xhrnew XMLHttp…...
面试题库（五）：并发编程
多线程类的使用 java线程同步有哪些方法、各自的优缺点synchronized 和ReentrantLock区别，可重入锁是什么？threadlocal有什么用Java中创建线程有几种方式？分别是？ 当主线程执行结束后，子线程还会继续执行下去吗？JUC中有哪些常用的集合？（项目中用到的）CopyOnWriteArray…...
Android FileProvider笔记
一、FileProvider是什么 通过FileProvider.getUriForFile(NonNull Context context, NonNull String authority, NonNull File file)方法获得一个有临时权限的Uri给客户端用来访问本APP文件。 当然看FileProvider类的注释更加详细 二、代码示例 <providerandroid:name&q…...
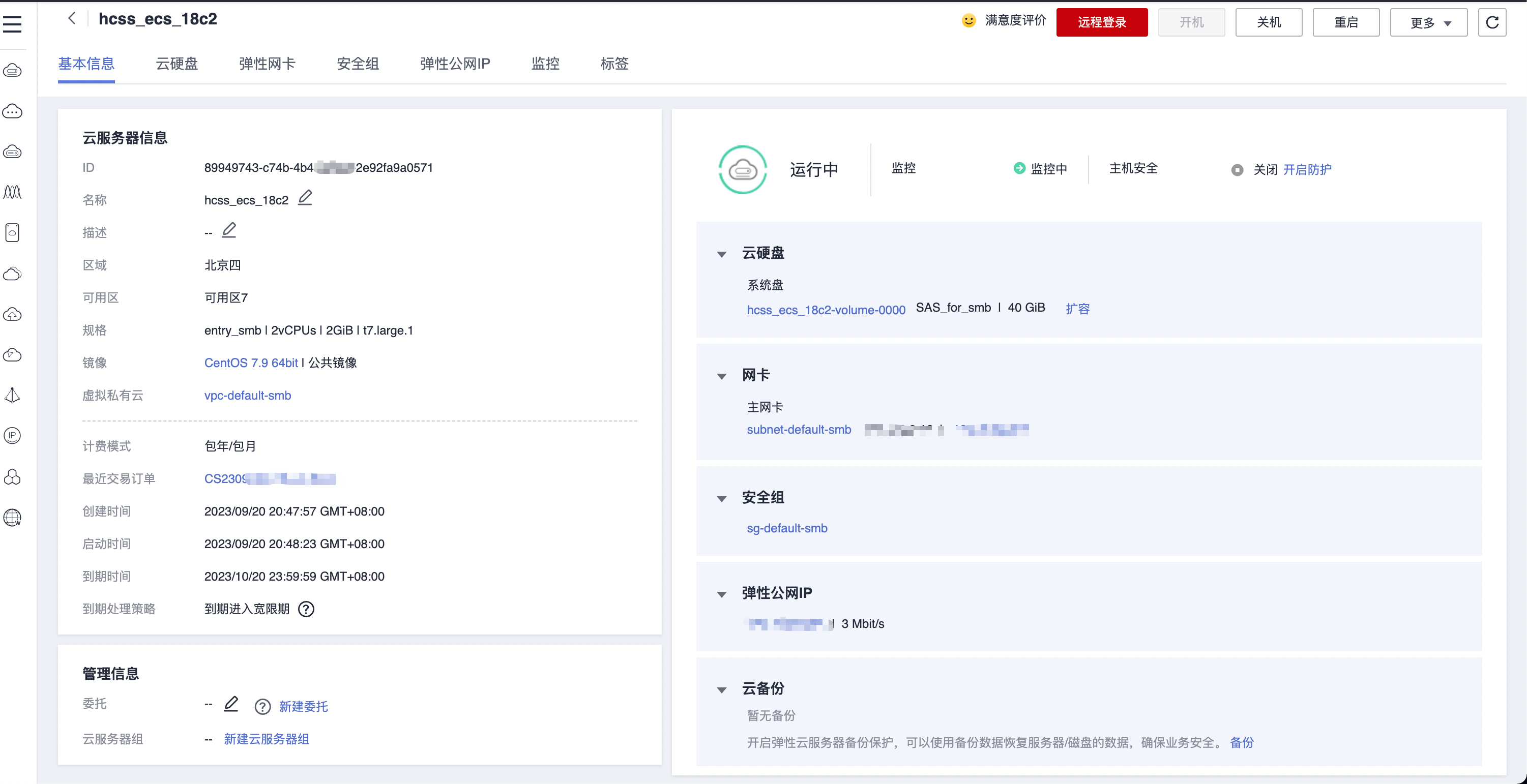
华为云云耀云服务器L实例评测 ｜云服务器选购
华为云耀云服务器 L 实例是一款轻量级云服务器，开通选择实例即可立刻使用，不需要用户再对服务器进行基础配置。新用户还有专享优惠，2 核心 2G 内存 3M 带宽的服务器只要 89 元/年，可以点击华为云云耀云服务器 L 实例购买地址去购买…...
2023-09-22 LeetCode每日一题（将钱分给最多的儿童）
2023-09-22每日一题 一、题目编号 2591. 将钱分给最多的儿童二、题目链接 点击跳转到题目位置 三、题目描述 给你一个整数 money ，表示你总共有的钱数（单位为美元）和另一个整数 children ，表示你要将钱分配给多少个儿童。 你…...
功能测试的重要性
前言 在软件开发领域，功能测试是确保软件质量的关键步骤之一。正如其名称所示，功能测试是验证软件产品是否具有其描述的功能和符合预期结果的过程。这种类型的测试非常重要，因为它不仅可以帮助团队检测潜在的缺陷并提高软件品质，…...
《Linux高性能服务器编程》--高级I/O函数
目录 1--Pipe() 2--dup() 和 dup2() 3--readv() 和 writev() 4--sendfile() 5--mmap() 和 munmap() 6--spice() 7--tea() 8--fcntl() 1--Pipe() #include <unistd.h> int pipe(int fd[2]); // 成功返回0，失败返回-1 pipe() 函数可用于创建一个管道&a…...
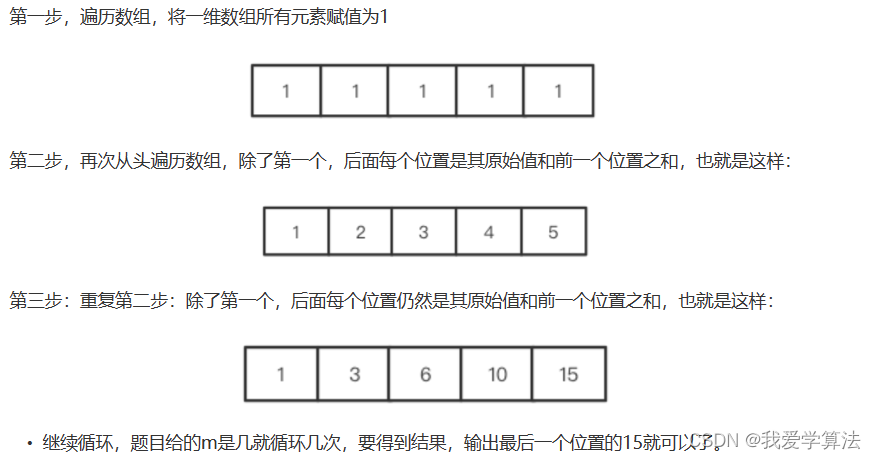
算法通关村 | 透彻理解动态规划
1. 斐波那契数列 1，1，2，3，5，8，13，..... f(n) f(n-1) f(n-2) 代码实现 public static int count_2 0;public int fibonacci(int n){if (n < 2){count_2;return n;}int f1 1;int f2 2;i…...
数据结构（持续更新）
嗯，怎么说数据结构果然很玄妙。按照能不能存储多行元素大致分为两类。 不能存好几行的数据包括pair，int，float，double，char，struct； 能存好几行的：map，unordered_map，list，vector，set，string，array。 1. pair “pair” 是 C++ 标准库中的一个模板类，它用于存储…...
nginx部署vue后显示500 Internal Server Error解决方案
前言 描述：当我配置好全部之后，通过 服务器 ip 地址访问，遇到报错信息：500 Internal Server Error。 今天部署vue前端项目一直报错500，无法显示出主页面。 一个以为是自己的dist位置没有访问正确或者nginx.conf的位…...
微调大型语言模型(一)：为什么要微调(Why finetune)?
今天我们来学习Deeplearning.ai的在线课程 微调大型语言模型(一)的第一课：为什么要微调(Why finetune)。 我们知道像GPT-3.5这样的大型语言模型(LLM)它所学到的知识截止到2021年9月，那么如果我们向ChatGPT询问2022年以后发生的事情，它可能会…...
【GO】网络请求例子
post请求;multipart/form-data类型 // 构建请求参数requestData : map[string]interface{}{"gb": "","code": "","reMemberInfo": map[string]interface{}{"shi": "","…...
泡泡玛特海外布局动作不断，开启东南亚潮玩盛会
近日，泡泡玛特海外布局动作不断，9月8日至10日，泡泡玛特2023 PTS潮流玩具展（下简称新加坡PTS）在新加坡滨海湾金沙成功举办，现场人气爆棚，三天吸引了超过2万观众入场，这也是泡泡玛特首…...
业务系统对接大模型的基础方案：架构设计与关键步骤
业务系统对接大模型：架构设计与关键步骤 在当今数字化转型的浪潮中，大语言模型（LLM）已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中，不仅可以优化用户体验，还能为业务决策提供…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学（Elliptic Curve Cryptography）是基于椭圆曲线数学理论的公钥密码系统，由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA，ECC在相同安全强度下密钥更短（256位ECC ≈ 3072位RSA…...
YSYX学习记录（八）
C语言，练习0： 先创建一个文件夹，我用的是物理机： 安装build-essential 练习1： 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件，随机修改或删除一部分，之后…...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录，但是由于这个树组件的节点越来越多，导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多，导致的浏览器卡顿，这里很明显就需要用到虚拟列表的技术&…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件，所以得把软件用docker打包起来，大部分功能都没问题，出了一个奇怪的事情。同样的代码，在本机上用vscode可以运行起来，但是打包之后在docker里出现了问题。使用的是dialog组件，…...
Android第十三次面试总结（四大 组件基础）
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成，用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机： onCreate() 调用时机：Activity 首次创建时调用。…...
基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）
考察一般的三次多项式，以r为参数： p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]； 此多项式的根为： 尽管看起来这个多项式是特殊的，其实一般的三次多项式都是可以通过线性变换化为这个形式…...
go 里面的指针
指针 在 Go 中，指针（pointer）是一个变量的内存地址，就像 C 语言那样： a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10，通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...