【算法与数据结构】JavaScript实现十大排序算法(一)
文章目录
- 关于排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 归并排序
关于排序算法
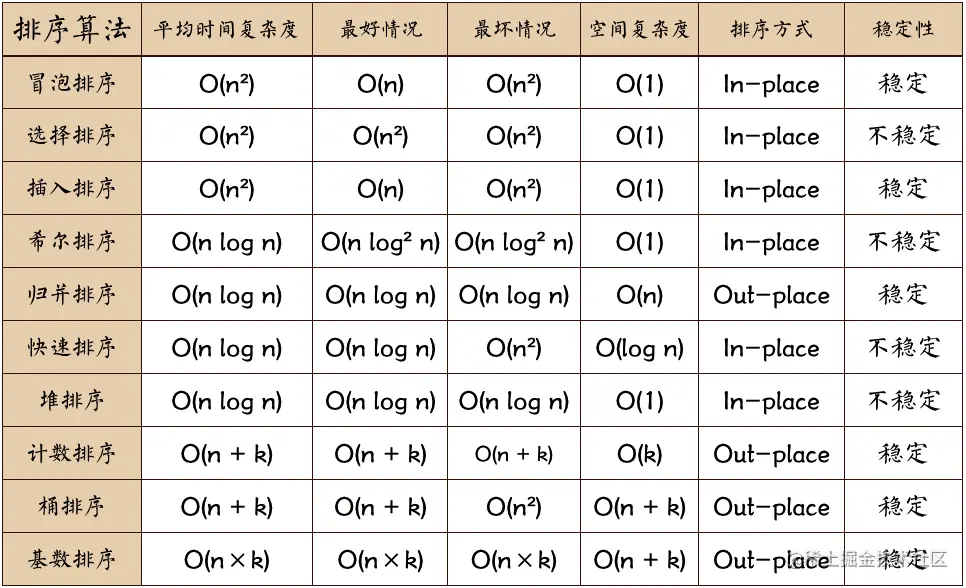
稳定排序: 在排序过程中具有相同键值的元素,在排序之后仍然保持相对的原始顺序。意思就是说,现在有两个元素a和b,a排在b的前面,且a==b,排序之后a仍然在b的前面,这就是稳定排序。
非稳定排序: 在排序过程中具有相同键值的元素,在排序之后可能会改变它们的相对顺序。意思是说,现在有两个元素a和b,在原始序列中a排在b前面,排序之后a可能会出现在b后面,它们的相对位置可能会发生变化。
原地排序: 在排序过程中不需要申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。这意味着在原地排序中,排序操作会直接修改原始数据,而不需要创建新的数据结构来存储排序后的结果。
非原地排序: 在排序过程中需要申请额外的存储空间来存储临时数据或排序结果,而不直接在原始数据上进行修改。
冒泡排序
基本思路: 通过相邻元素之间的比较和交换,将排序码小的元素逐渐从底部移向顶部。由于整个排序的过程就像水底下的气泡一样逐渐向上冒,因此称为冒泡排序。
操作步骤:
- 比较相邻的两个元素。如果第一个元素比第二个元素大,就交换这两个元素;
- 重复上述步骤,直到数组末尾;
- 重复上述两个步骤,直到完成排序。
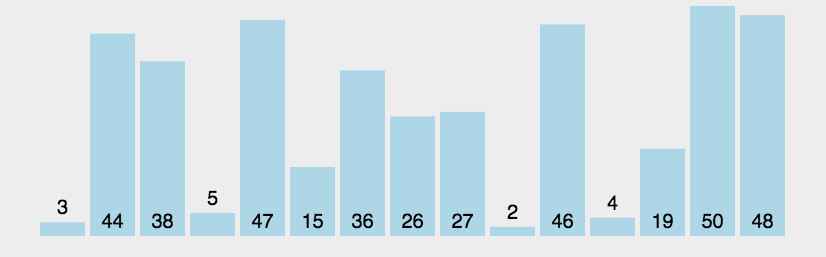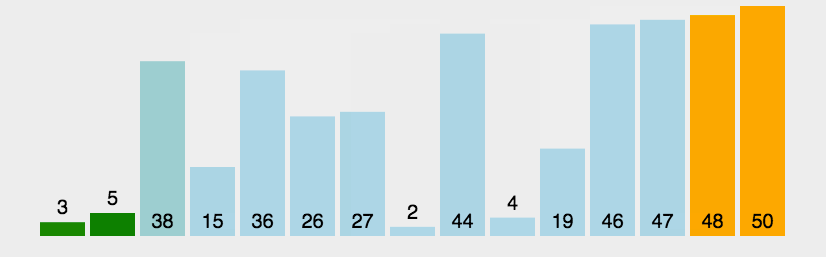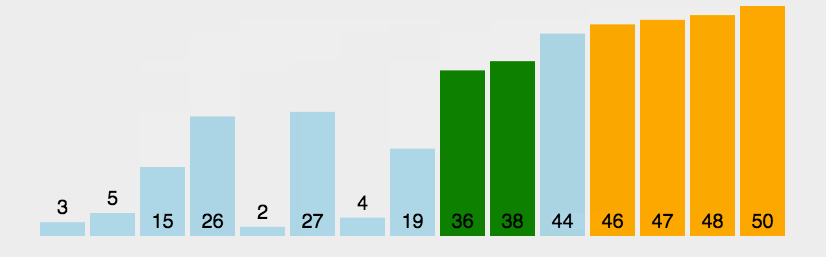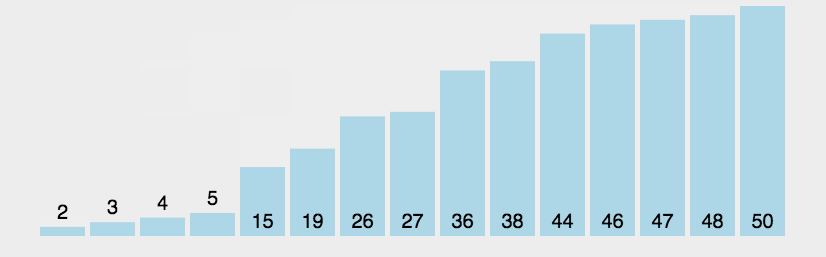
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function BubbleSort(arr) {for (let i in arr) {// 每次循环都能找到一个最大的数放在最右边for (let j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {let temp = arr[j]arr[j] = arr[j + 1]arr[j + 1] = temp}}}console.log(arr);return arr}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]BubbleSort(a)</script>
总结: 稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(n²)。
选择排序
基本思路: 首先在未排序序列中找到最小(大)元素,存放到排序的起始位置,接着再从剩余末排序元素中继续寻找最小(大)元素,放到已排序序列的起始位置。以此类推,直到所有的元素均已排序完毕。
操作步骤:
- 在数列范围内找到最小(大)元素,与起始位置元素进行交换;
- 除已经排序过的元素外,在剩余数列范围内找到最小(大)元素,与剩余数列的起始位置元素进行交换。
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function SelectionSort(arr) {for (let i in arr) {// 声明一个变量,用来接收当前最小值的下标let min = ifor (let j = i; j < arr.length; j++) {if (arr[j] < arr[min]) {min = j}}let temp = arr[i]arr[i] = arr[min]arr[min] = temp}console.log(arr);return arr}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]SelectionSort(a)</script>
分析: 不稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(n²)。
插入排序
基本思路: 将数组分为两部分,一部分是已排序的,一部分是未排序的。初始时,已排序部分只包含数组的第一个元素,然后依次将未排序部分的元素插入已排序部分,使得已排序部分仍然保持有序。
操作步骤:
- 将第一个数作为基准,取出第二个数与其进行比较,如果比它大就放右边,比它小就放左边;
- 取出第三个数,与前一个数进行比较,比它大就放右边,比它小就再往前一个数进行比较,直到遇到一个比它小的数;
- 一直重复上述步骤
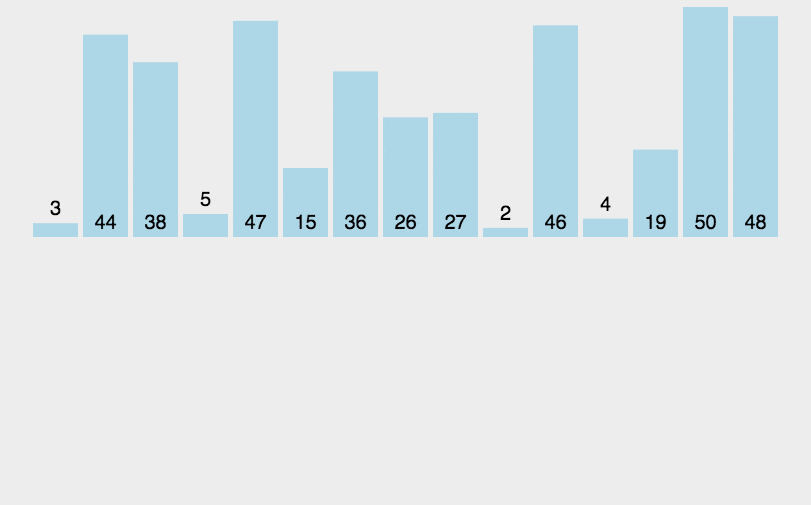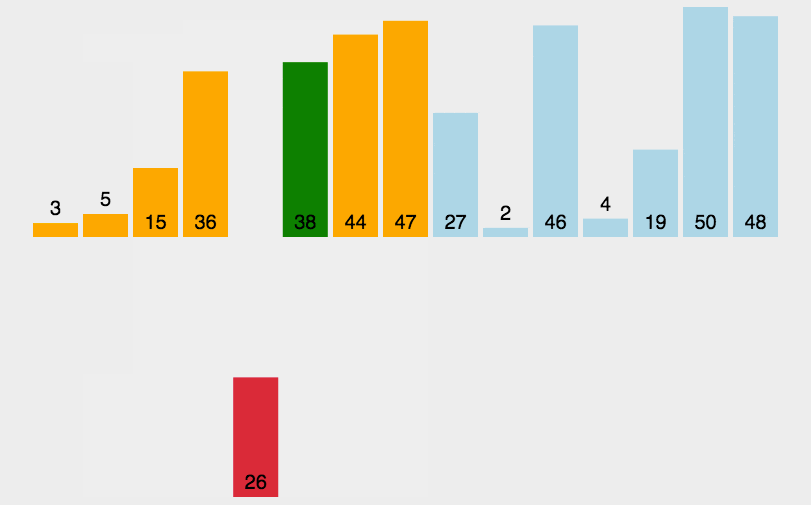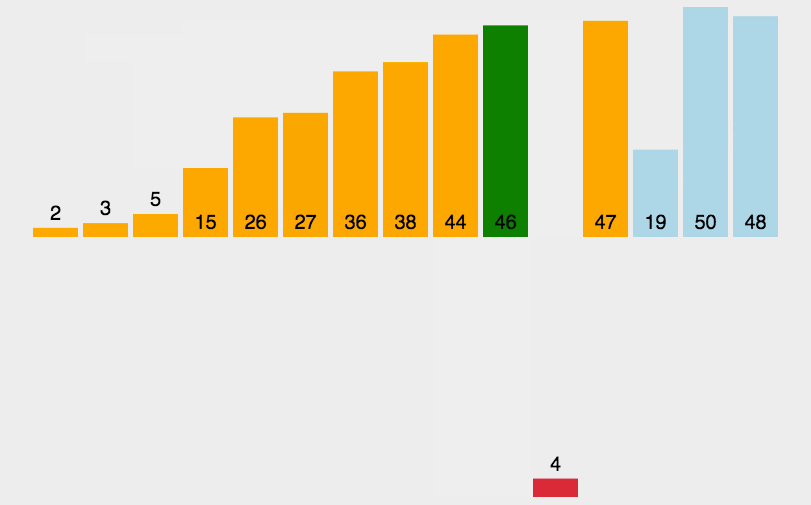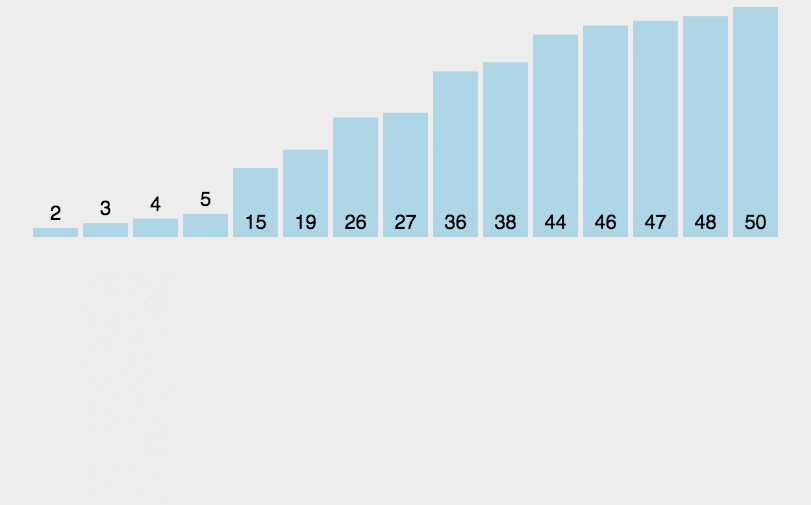
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function InsertionSort(arr) {// 以第一个数作为基准for (let i = 1; i < arr.length; i++) {let temp = arr[i]let j;// 如果遍历的元素大于取出的元素,则遍历过的元素都需要后移一位for (j = i - 1; j >= 0 && a[j] > temp; j--) {arr[j + 1] = arr[j]}arr[j + 1] = temp}console.log(arr);}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]InsertionSort(a)</script>
分析: 稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(n²)。
希尔排序
基本思路: 它是插入排序的一种改进版本,通过将原始数组分成多个子序列,利用插入排序对子序列进行排序,最终合并成一个有序序列。
操作步骤:
- 选择一个增量序列(间隔序列),通常初始增量为数组长度的一半,然后逐渐减小增量;
- 按照增量将原始数组分成多个子序列。每个子序列可以视为一个小型数组;
- 对每个子序列应用插入排序算法,将子序列中的元素进行排序;
- 逐渐缩小增量,重复上述步骤,直到增量为 1;
- 最后一次增量为 1 时,整个数组被视为一个序列,再次应用插入排序。
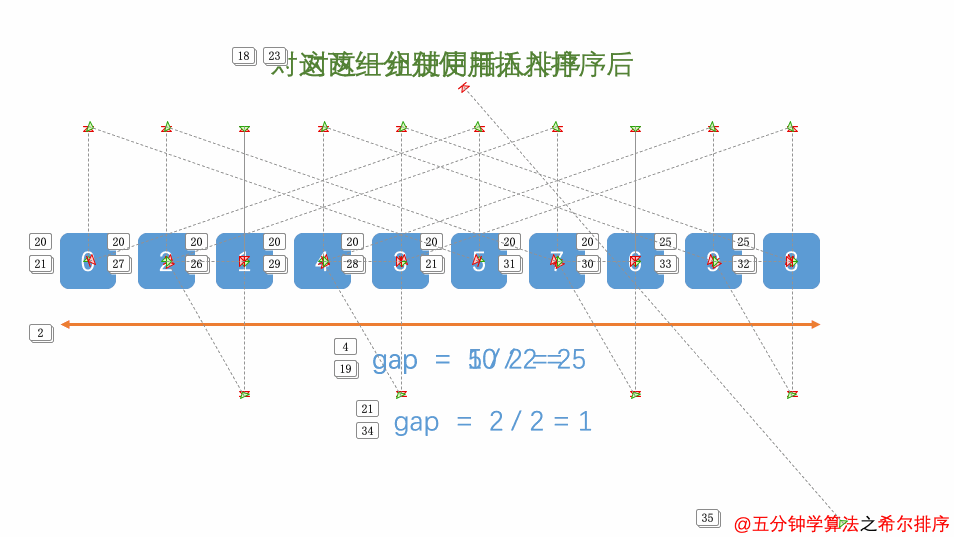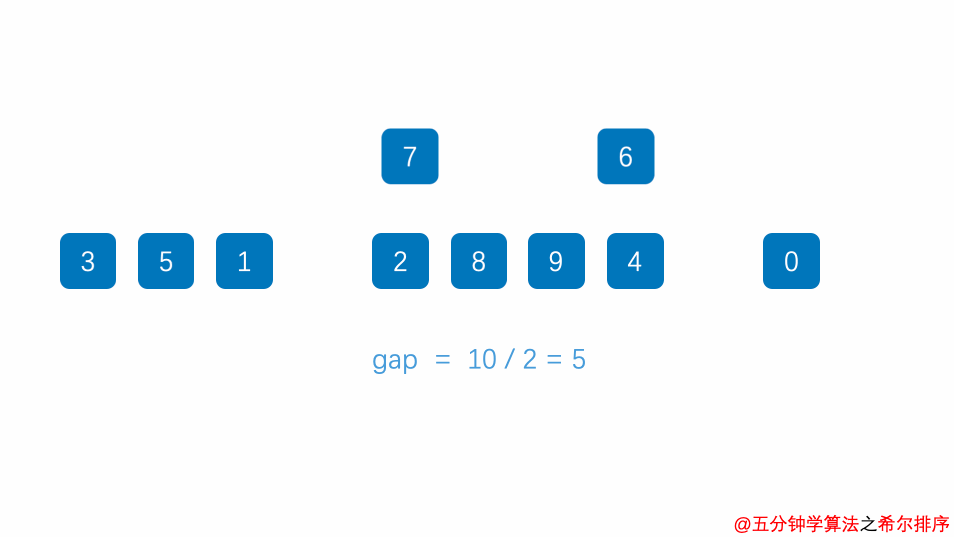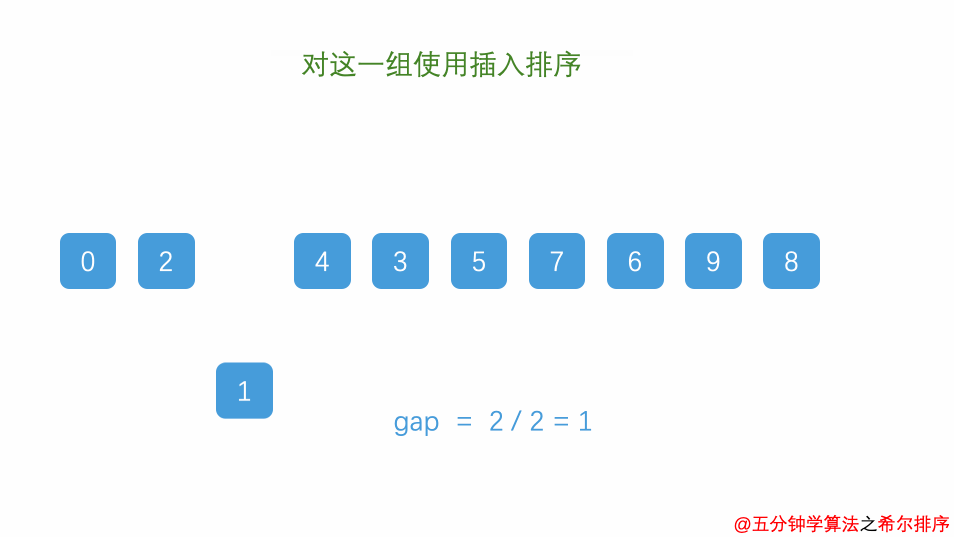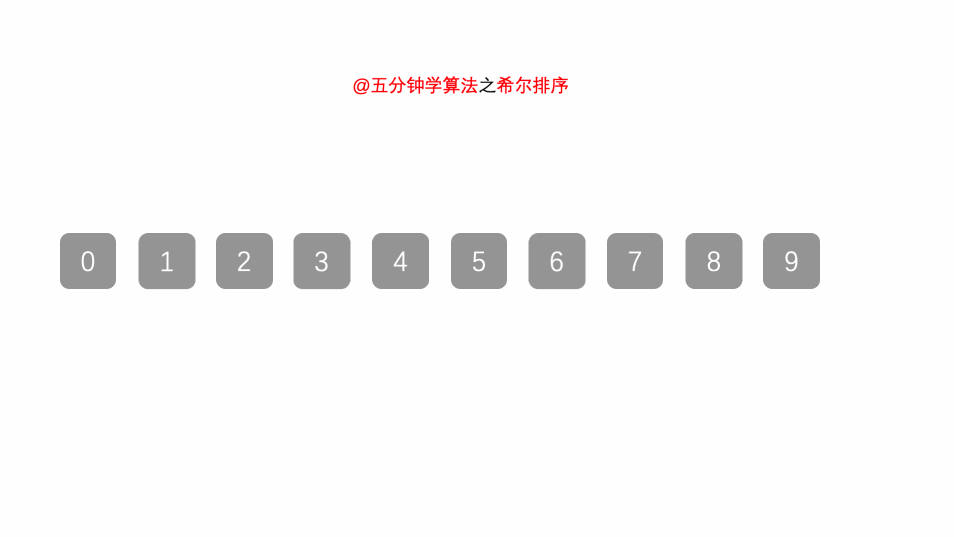
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function ShellSort(arr) {// 选择初始的增量(gap)为数组长度的一半Math.floor(arr.length / 2)for (let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap / 2)) {// 对每个子序列进行插入排序for (let i = gap; i < arr.length; i++) {const temp = arr[i]let j;for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {arr[j + gap] = arr[j]}arr[j + gap] = temp}}console.log(arr);}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]ShellSort(a)</script>
分析: 不稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(nlog(n))。
归并排序
基本思路: 它是一种基于分治策略的排序算法,通过将待排序的数组分割成若干个子序列,分别排序后再合并这些子序列,以达到整体有序的目的。归并排序的主要步骤包括分割、排序和合并三个阶段。
操作步骤:
- 分割:将待排序的数组分成两个大致相等的子数组,递归地对这两个子数组进行排序;
- 排序:递归地对每个子数组进行排序,直到子数组的长度为1(只有一个元素),此时认为它是有序的;
- 合并:将排好序的子数组合并成一个新的有序数组,这一步的关键是将两个有序的子数组合并成一个更大的有序数组。

例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function MergeSort(arr) {if (arr.length <= 1) return arr;// 分割数组const middle = Math.floor(arr.length / 2)const left = arr.slice(0, middle)const right = arr.slice(middle)// 递归分割+排序const leftSort = MergeSort(left)const rightSort = MergeSort(right)return SequencSort(leftSort, rightSort)}function SequencSort(left, right) {let result = []let leftIndex = 0;let rightIndex = 0;// 合并两个有序数组while (leftIndex < left.length && rightIndex < right.length) {if (left[leftIndex] < right[rightIndex]) {result.push(left[leftIndex])leftIndex++} else {result.push(right[rightIndex])rightIndex++}}// 将剩余的元素添加到结果中return result.concat(left.slice(leftIndex), right.slice(rightIndex))}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]MergeSort(a)</script>
分析: 稳定排序,空间复杂度为O(n),时间复杂度为O(nlog(n))。
相关文章:

【算法与数据结构】JavaScript实现十大排序算法(一)
文章目录 关于排序算法冒泡排序选择排序插入排序希尔排序归并排序 关于排序算法 稳定排序: 在排序过程中具有相同键值的元素,在排序之后仍然保持相对的原始顺序。意思就是说,现在有两个元素a和b,a排在b的前面,且ab&…...

IntelliJ IDEA使用——插件推荐
官网插件库:https://plugins.jetbrains.com/search 代码规范检测:Alibaba Java Coding Guidelines码云:Giteemybatis插件:MyBatisX多颜色括号:Rainbow Brackets操作快捷键提示:Key Promoter X力扣ÿ…...

编写一个会导致死锁的程序,将怎么解决?
死锁发生在两个或多个线程互相等待对方释放资源的情况下。下面是一个可能导致死锁的情况: public class DeadlockExample {private static final Object lock1 = new Object();private static final Object lock2 = new...
Java JVM分析利器JProfiler 结合IDEA使用详细教程
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、JProfiler是什么?二、我的环境三、安装步骤1.Idea安装JProfiler插件1.下载程序的安装包 四、启动 前言 对于我们Java程序员而言,肯…...
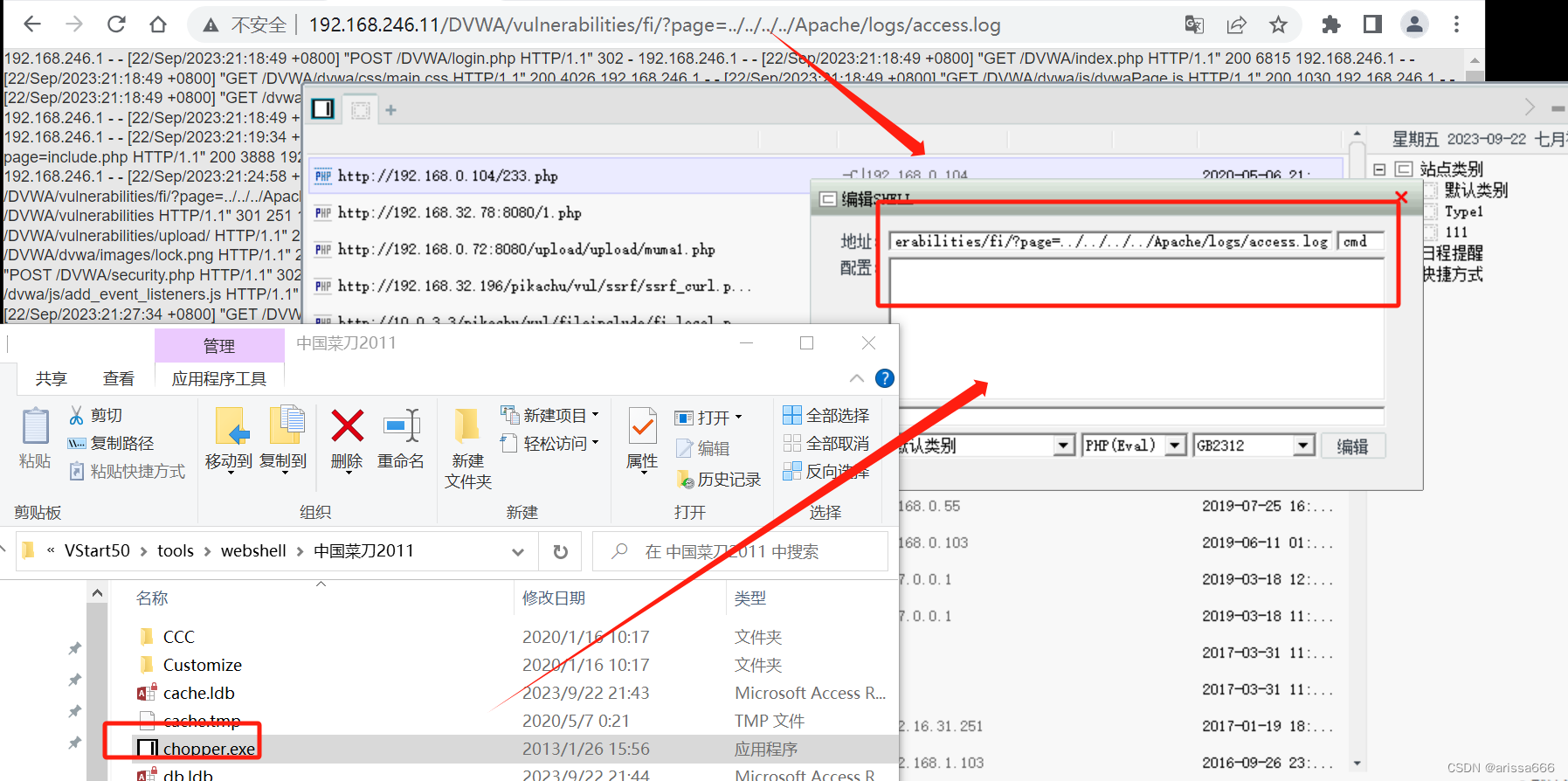
包含日志文件
原理:某个PHP文件存在本地包含漏洞,却无法上传正常文件,包含漏洞却不能利用,攻击者就有可能会利用apache日志文件来入侵。 Apache服务器运行后会生成两个日志文件,这两个文件是access.log(访问日志)和error.log(错误日…...

李航老师《统计学习方法》第2章阅读笔记
感知机(perceptron)时二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面 想象一下在一个平面…...
ruoyi框架修改左侧菜单样式
菜单效果 ruoyi前端框架左侧的菜单很丑,我们需要修改一下样式,下面直接看效果。 修改代码 1、sidebar.scss .el-menu-item, .el-submenu__title {overflow: hidden !important;text-overflow: ellipsis !important;white-space: nowrap !important;//…...

【已解决】PyCharm里的黄色波浪线
问题描述 有时候在PyCharm中某些代码下面会有黄色波浪线。 问题解释 黄色波浪线只是提示这段代码不规范,但对程序的运行并没有本质影响。...
)
设计模式:策略模式(C++实现)
策略模式(Strategy Pattern)是一种行为设计模式,它定义了一系列的算法,并将每个算法封装成独立的对象,使得它们可以互相替换。下面是一个使用C实现策略模式的示例: #include <iostream>// 抽象策略类…...

网络安全深入学习第二课——热门框架漏洞(RCE—Thinkphp5.0.23 代码执行)
文章目录 一、什么是框架?二、导致框架漏洞原因二、使用步骤三、ThinkPHP介绍四、Thinkphp框架特征五、Thinkphp5.0.23 远程代码执行1、漏洞影响范围2、漏洞成因 六、POC数据包Windows下的Linux下的 七、漏洞手工复现1、先Burp抓包,把抓到的请求包发送到…...

Pdf文件签名检查
如何检查pdf的签名 首先这里有一个已经签名的pdf文件,通过pdf软件可以看到文件的数字签名。 图1为签名后的文件,图2为签名后文件被篡改。 下面就是如何代码检查这里pdf文件的签名 1.引入依赖 <dependency><groupId>org.projectlombok<…...

web前端之float布局与flex布局
float布局 <style>.nav {overflow: hidden;background-color: #6adfd0; /* 导航栏背景颜色 */}.nav a {float: left;display: block;text-align: center;padding: 14px 16px;text-decoration: none;color: #000000; /* 导航栏文字颜色 */}.nav a:hover {background-col…...

expected ‘,’ after expression in R【R错误】
出现如下错误: 在红色叉的位置,会有提示“expected . after expression”,咋一看出现红色叉的位置没有任何的错误,怎么会出现错误呢? 解决办法: 寻找这个代码第一次出现红色叉的位置,看其是否…...

算法|图论 2
LeetCode 695- 岛屿的最大面积 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给你一个大小为 m x n 的二进制矩阵 grid 。 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求…...

使用C#实现服务端与客户端的简陋聊天
服务端代码: using System; using System.Net.Sockets; using System.Net; using System.IO;//服务器程序 namespace CSharpStudy_09_21 {class Program{static void Main(string[] args){int port 8865;TcpClient tcpClient;//创建tcp对象IPAddress[] serverIp Dns.GetHost…...
生成式模型和判别式模型区别
目录 1.概念 2.定义 3.举例 (1)例子 A (2)例子 B 4.特点 5.优缺点 6.代表算法 1.概念 首先我们需要明确,两种不同的模型都用于监督学习任务中。监督学习的任务就是从数据中学习一个模型,并用…...

【kafka实战】03 SpringBoot使用kafka生产者和消费者示例
本节主要介绍用SpringBoot进行开发时,使用kafka进行生产和消费 一、引入依赖 <dependencies><dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId></dependency><depen…...
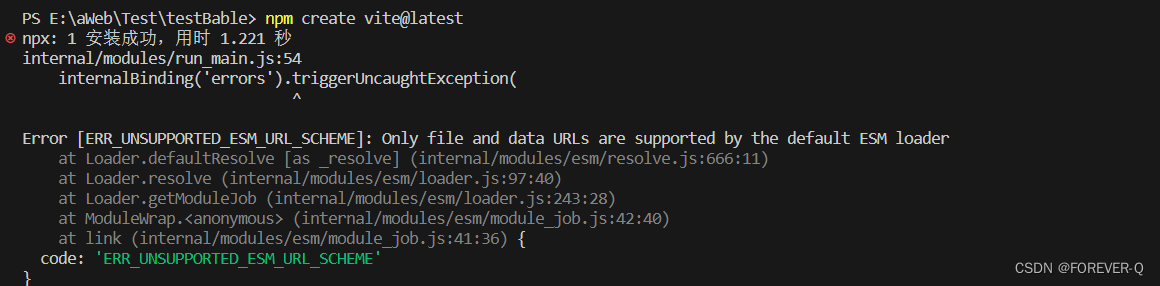
Only file and data URLs are supported by the default ESM loader
1.版本问题 说明:将node版本提高就可以了。 2.nvm 说明:如果不想重复安装node版本,那么可以参考本人的nvm文档. nvm版本控制工具_FOREVER-Q的博客-CSDN博客...
LeetCode01
LeetCode01 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和 为目标值 target 的那两个整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你…...

计算机网络高频面试题集锦
问题1:谈一谈对OSI七层模型和TCP/IP四层模型的理解? 回答点:七层模型每层对应的作用及相关协议、为什么分层、为什么有TCP/IP四层模型 参考: 1、OSI七层参考模型是一个ISO组织所提出的一个标准参考分层模型,它按照数…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
