当前位置： 首页 > news >正文

科目三基础四项（一）

news 2025/12/17 5:27:16

​ 第一天，基础操作，仪表，方向，挡位

按照模块来

1、方向盘两手在两侧

​

编辑

转向时的角度，只用：向左540°，向右180°

向左打和向右打的角度要抵消，回正

掉头向左打满再回

注意每旋转180度的交叉手，这个很难用语言形容

 2、挡位：

我的考场是：

1

3

5

空挡

空挡

空挡

2

4

R

注意换挡的时候，手虚抓，用力的方向。

中央的空挡如果在两侧会自动弹回，停车需要确认。

升档一档一档升，降档无所谓

每一档对应有速度限制，要在限制内开车

1

0-10

2

10-20

3

20-30

4

30-40

5

40-50

换挡时，处于下一档的速度区间，最好是中间值。

比如在一档，加速到15，换二档

3、上车的四件事

从车头方向上车，调节座椅前后，调节靠背，调节安全带

4、离合

理解成两个相互咬合的齿轮，踩离合会让齿轮分开，松开离合齿轮咬合，这个是基础

在这个基础上，可以理解一些熄火的事件。

比如换挡，要先加速到合适的速度；

松开油门，离合器踩到底；

换挡；

缓缓松开离合器；

踩油门保持速度。

减速时要先踩离合再踩刹车

这是因为如果直接踩刹车，齿轮还处于咬合状态，但是车轮一边的齿轮不转了。

发动机累积的动力释放不出去，会损伤发动机，自我保护选择熄火。

5、起步

离合刹车踩到底，缓缓抬起离合器，直到出现震动感后，松开刹车，车辆向前滑行，达到5公里以上后，松开离合器就不会熄火了。

半坡起步同样适用。

6、怠速

发动机没有加油门的速度，不挂档也会往前跑，教练车10km，发动机转速800r/min

相关文章：

科目三基础四项（一）

​ 第一天，基础操作，仪表，方向，挡位 按照模块来 1、方向盘两手在两侧 ​ 编辑 转向时的角度，只用：向左540，向右180 向左打和向右打的角度要抵消，回正 掉头向左打满再回 注意…...

编程日记 2023/9/23 17:08:16

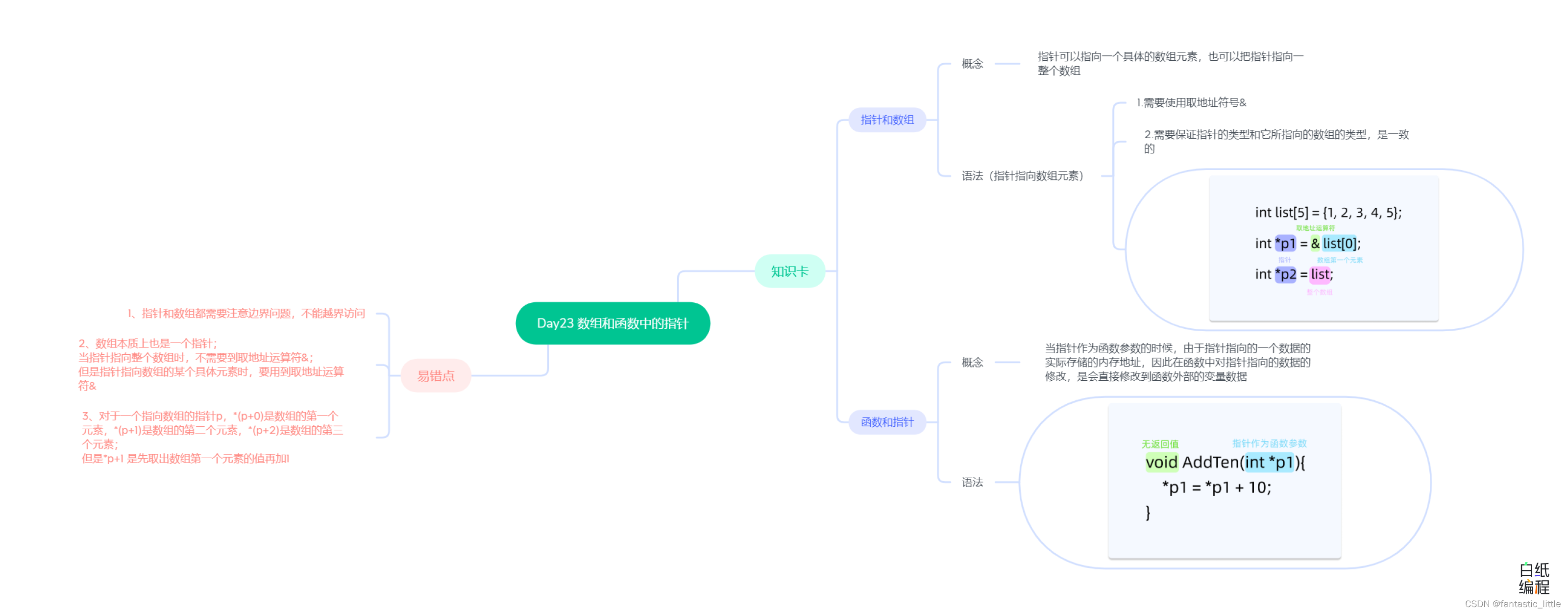
C语言入门Day_24 函数与指针

目录 前言： 1.指针和数组 2.函数和指针 3.易错点 4.思维导图 前言： 我们知道数组是用来存储多个数据的，以及我们可以用指针来指向一个变量。那么我们可以用指针来指向一个数组中的数据么？ 指针除了可以像指向一个变量一样指…...

编程日记 2023/9/23 17:07:15

9月21日，每日信息差

今天是2023年9月21日，以下是为您准备的14条信息差 第一、谷歌高管已经广泛讨论了在2027年之前将博通作为人工智能芯片供应商的可能性 第二、清华系团队宣布研发出千亿参数“制药版ChatGPT”，覆盖药物立项、临床前研究、临床试验的各阶段，作…...

编程日记 2023/9/23 17:06:14

【FAQ】安防监控系统/视频云存储/监控平台EasyCVR服务器解释器出现变更该如何修改？

安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快，可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等，以及支持厂家私有协议与SDK接入，包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...

编程日记 2023/9/23 17:05:13

Python手写人脸识别

Python手写人脸识别 引言 人脸识别是一种通过计算机视觉和模式识别技术来识别和验证人脸的技术。Python是一种广泛使用的编程语言，它提供了许多强大的库和工具来实现人脸识别。 在Python中，可以使用多种方法来实现人脸识别，包括基于特征提取的方法、基于深度学习的方法等…...

编程日记 2023/9/23 17:03:09

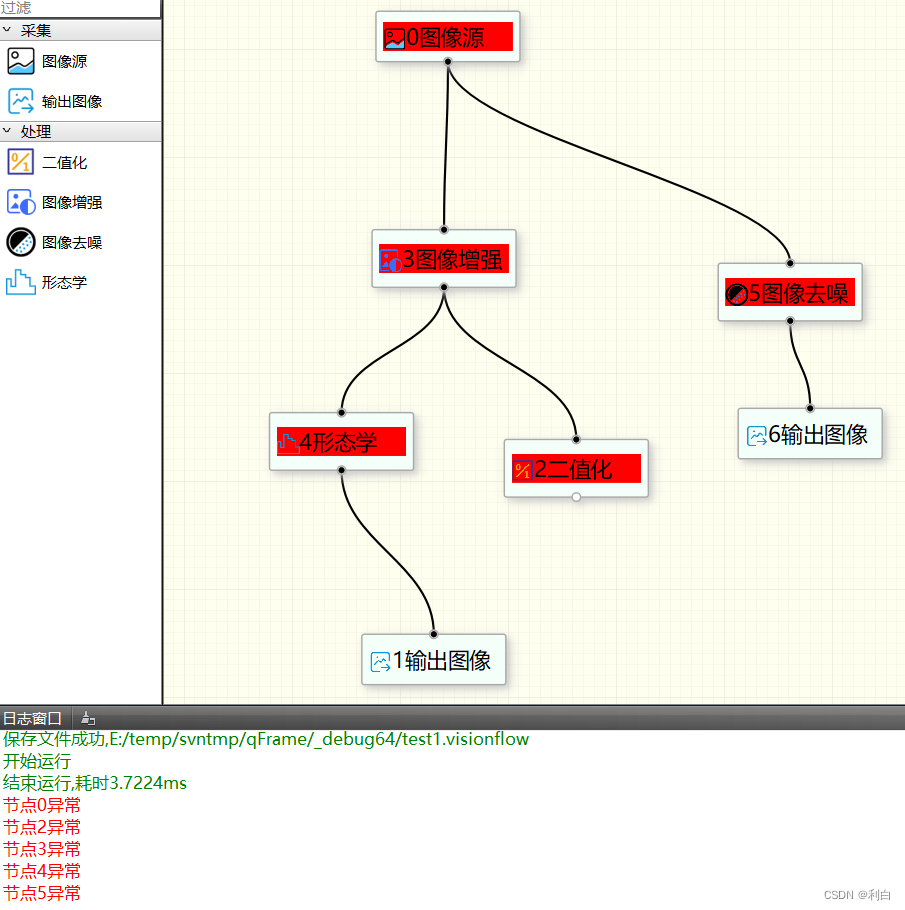
我的Qt作品（19）使用Qt写一个轻量级的视觉框架---第2章，仿海康VM实现思维导图拖拽方式的算法流程图

上次写的第1章介绍了主界面的设计。 https://blog.csdn.net/libaineu2004/article/details/130277151 本次是第2章，主要介绍流程图的运行。 目前市面上视觉框架很多，主要有列表图方式和流程图方式。海康VM的流程图方式比较受用户的喜爱和欢迎&#xf…...

编程日记 2023/9/23 17:02:08

仿写Timi记账

项目仿照Timi记账，本 APP 仅用作学习，如有侵权联系删除，项目地址：Timi记账 TIMI记账项目 简单功能对于tableview向上延伸部分采用了insertSubview形式：添加特殊字体添加.ttf文件获取plist文件数据 计算器功能说明简单逻…...

编程日记 2023/9/23 17:01:06

Java语言实现 比较两个Date日期的先后

在 Java 中，可以使用 Date 类的 compareTo() 方法或 before()、after() 方法来比较两个 Date 类型的日期的先后顺序。 使用 compareTo() 方法： Date date1 ...; // 第一个日期 Date date2 ...; // 第二个日期int result date1.compareTo(date2); if (…...

编程日记 2023/9/23 16:56:59

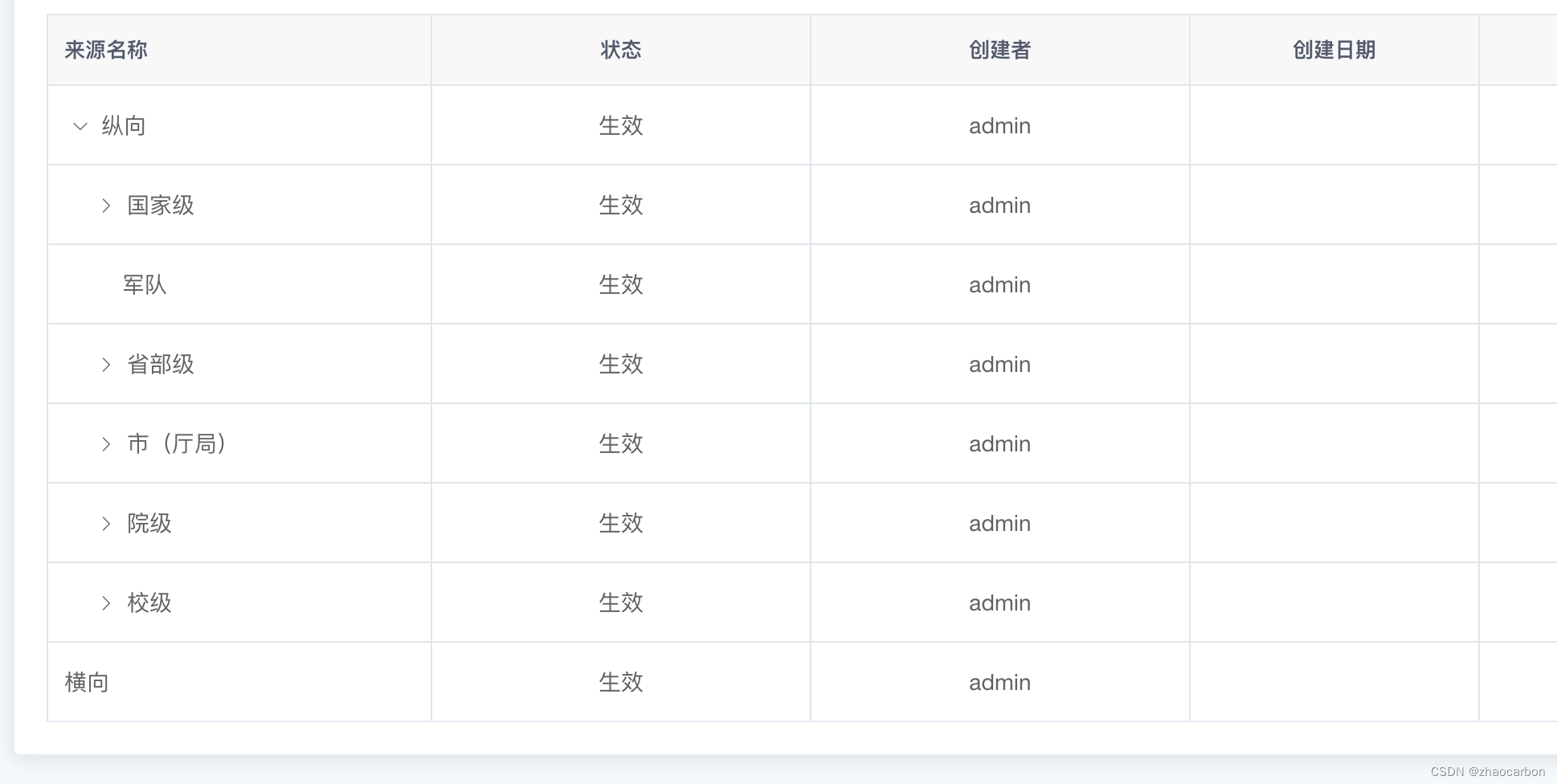
el-table 指定层级展开

先来看看页面默认全部展开时页面的显示效果&#xff1a;所有节点被展开&#xff0c;一眼望去杂乱无章&#xff01; 那么如何实现只展开指定的节点呢&#xff1f;最终效果如下&#xff1a;一眼看去很舒爽。 干货上代码&#xff1a; <el-table border v-if"refreshTabl…...

编程日记 2023/9/23 16:55:58

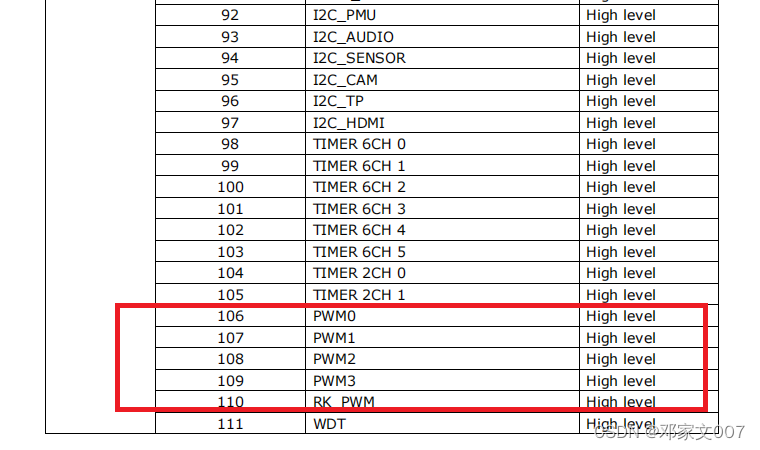
3288S Android11 适配红外遥控功能（超详细）

目录 一、rk3288平台红外遥控介绍二、原理图分析三、配置设备树并使能红外遥控功能四、打开红外打印功能&#xff0c;查看红外遥控的用户码和键值五、将查看到的红外遥控用户码和键值添加到设备树和.kl文件六、Android红外遥控.kl文件映射知识和使用添加新的.kl文件七、补充&am…...

编程日记 2023/9/23 16:53:54

Linux高性能服务器编程 学习笔记 第三章 TCP协议详解

与IP协议相比&#xff0c;TCP协议更靠近应用层&#xff0c;因此在应用程序中有更强的可操作性。一些重要的socket选项都和TCP协议相关。 本章从以下方面讨论TCP协议&#xff1a; 1.TCP头部信息。TCP头部信息出现在每个TCP报文段中&#xff0c;用于指定通信的源端端口号、目的端…...

编程日记 2023/9/23 16:52:54

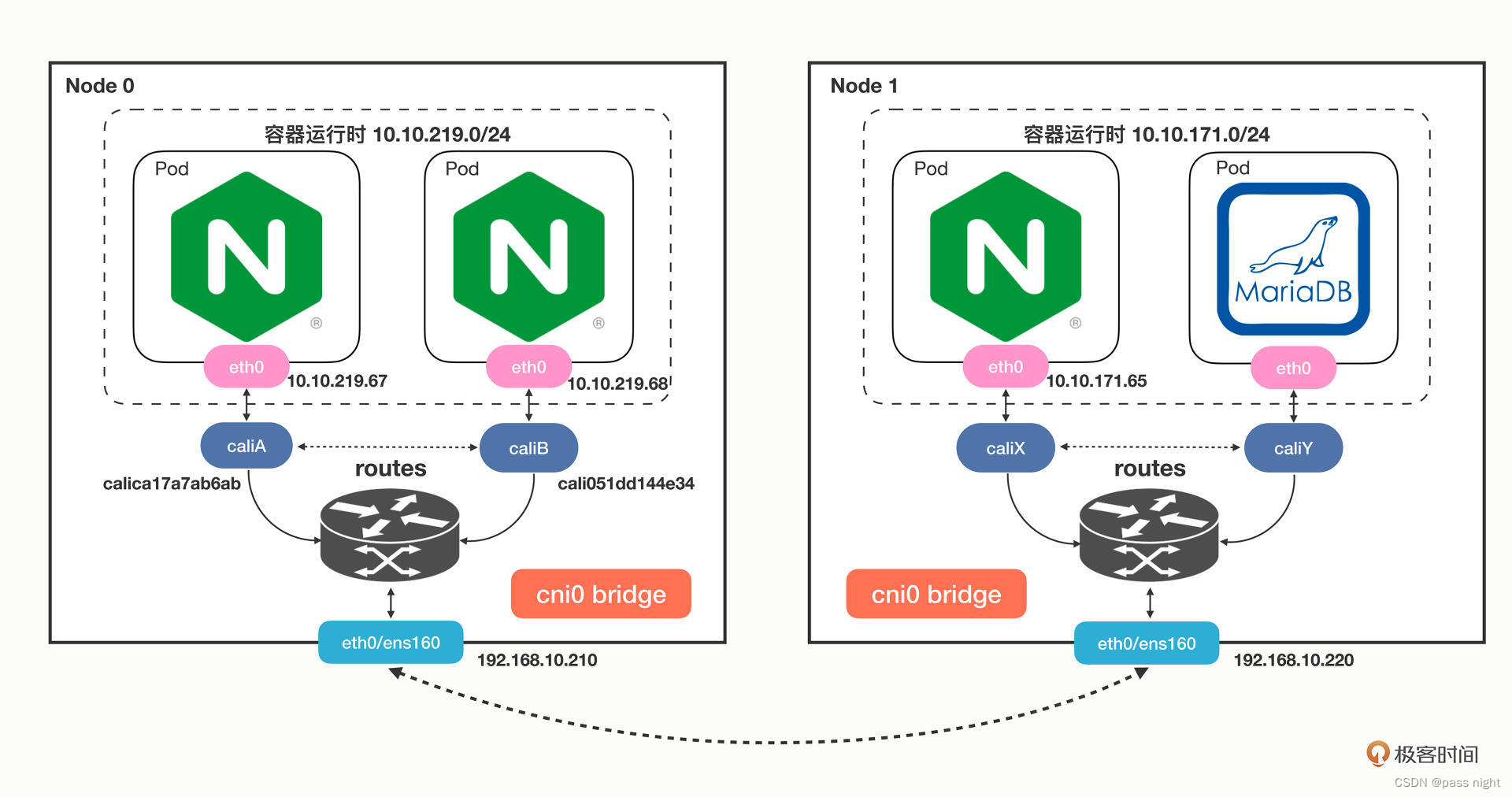
【云原生】Kubernetes学习笔记

部署 在部署前强调几点 不要使用IPv6, 很多组件都不支持IPv6不要使用最新版本, 最新版本非常不稳定, 甚至可能存在无法运行的bug不要版本更新, 安装后就将版本固定下来, 新的版本可能会引入新功能, 或移除旧功能, 导致Kubernetes无法运行 Kubeadm介绍 K8s是由多个模块构成的…...

编程日记 2023/9/23 16:49:49

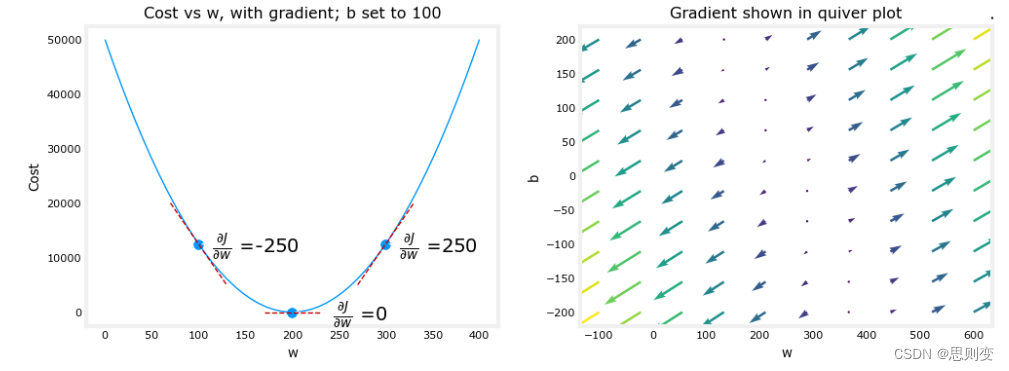
[Machine Learning][Part 2]监督学习的实现

目录 线性模型实现&#xff1a; cost function &#xff1a;代价函数或者损失函数——衡量模型优劣的一个指标 理论&#xff1a; 代码实现: 梯度下降——自动寻找最小的cost function 代价函数 梯度的概念&#xff1a; 梯度下降公式&#xff1a; 实现一个简单的监督学习…...

编程日记 2023/9/23 16:48:48

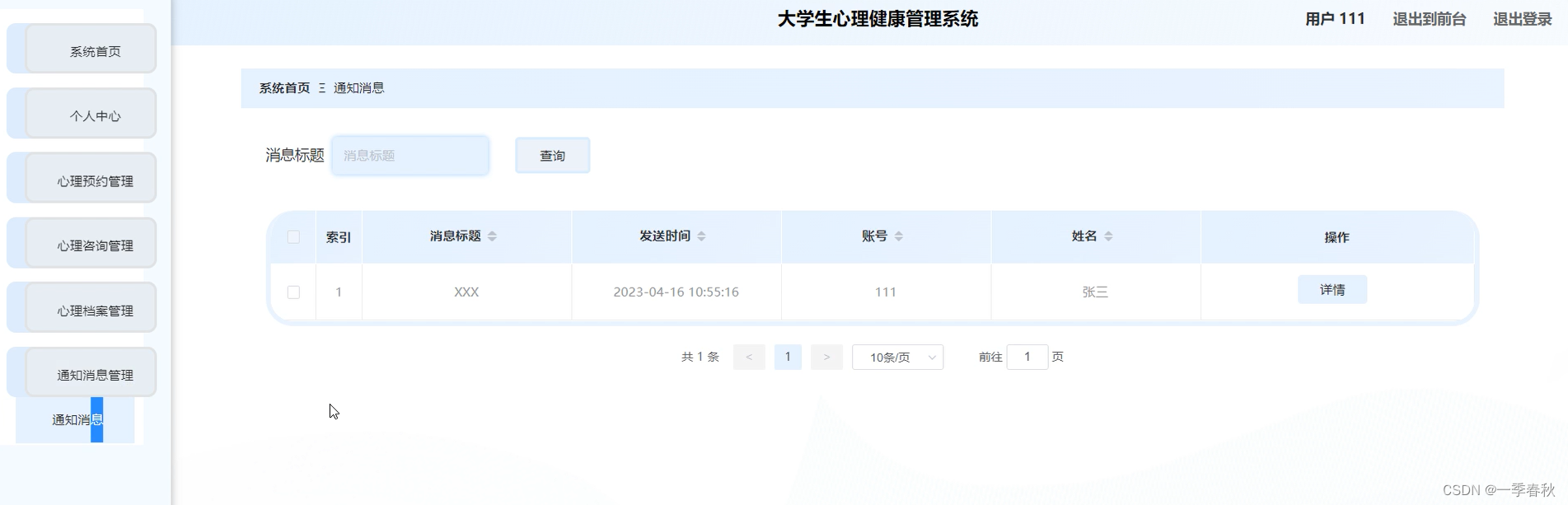
【计算机毕业设计】基于SpringBoot+Vue大学生心理健康管理系统的开发与实现

博主主页&#xff1a;一季春秋博主简介&#xff1a;专注Java技术领域和毕业设计项目实战、Java、微信小程序、安卓等技术开发&#xff0c;远程调试部署、代码讲解、文档指导、ppt制作等技术指导。主要内容&#xff1a;毕业设计(Java项目、小程序等)、简历模板、学习资料、面试题…...

编程日记 2023/9/23 16:47:47

下载水果FLStudio21.2软件安装更新教程

编曲是一种对音乐创作过程中涉及的元素和步骤进行组织和安排的艺术形式。对于想要学习编曲的人来说&#xff0c;以下是一些有用的建议&#xff1a; 1. 学习基础知识 在开始学习编曲之前&#xff0c;你需要掌握一些基础知识&#xff0c;例如音乐理论、乐器演奏和数字音乐制作技…...

编程日记 2023/9/23 16:46:46

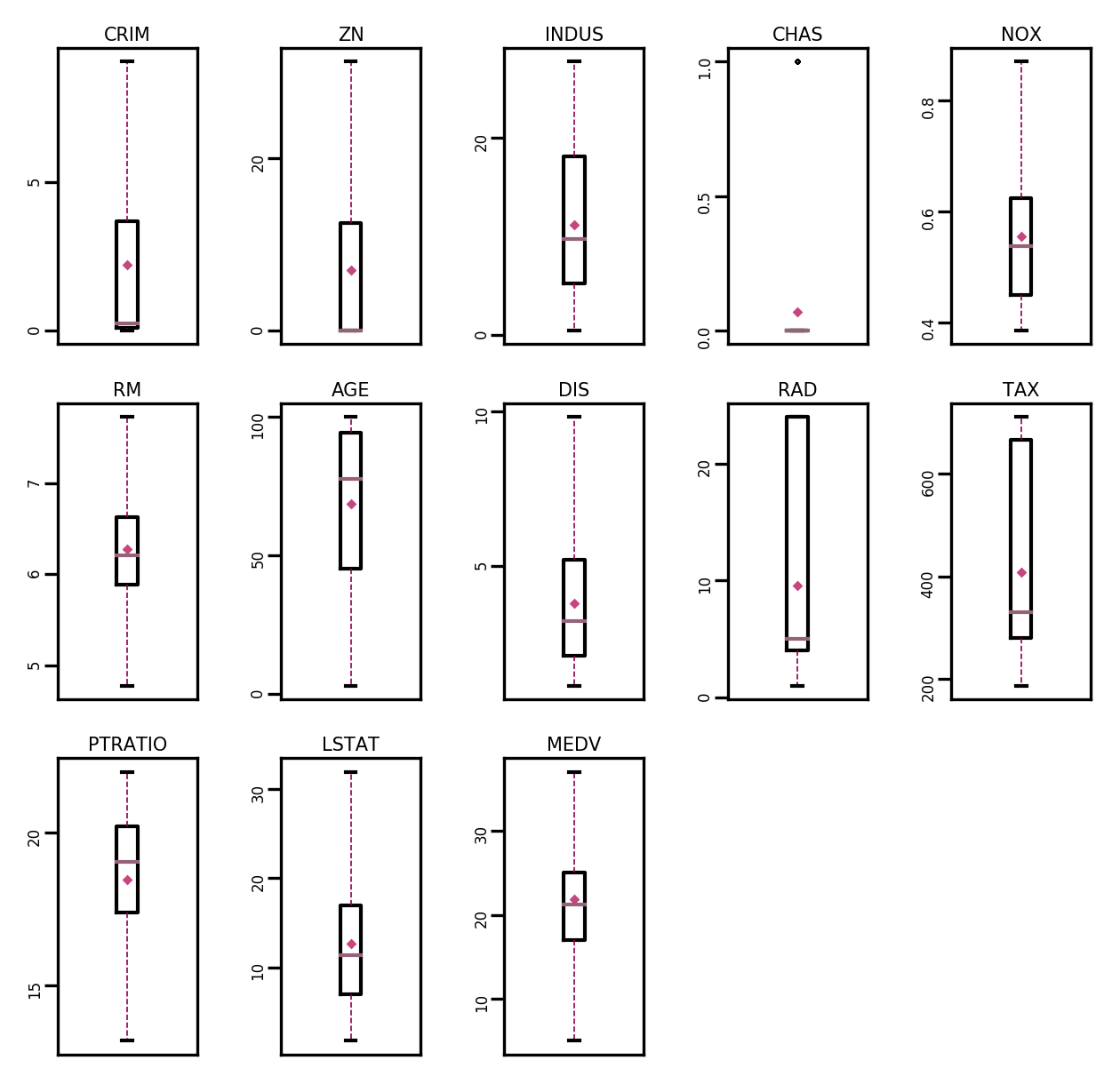
人工智能机器学习-飞桨神经网络与深度学习

飞桨神经网络与深度学习-机器学习 目录 飞桨神经网络与深度学习-机器学习 1.机器学习概述 2.机器学习实践五要素 2.1.数据 2.2.模型 2.3.学习准则 2.4.优化算法 2.5.评估标准 3.实现简单的线性回归模型 3.1.数据集构建 3.2.模型构建 3.3.损失函数 3.4.模型优化 3…...

编程日记 2023/9/23 16:45:44

linux部署页面内容

/bin&#xff1a;该目录包含了常用的二进制可执行文件&#xff0c;如ls、cp、mv、rm等等。 /boot&#xff1a;该目录包含了启动Linux系统所需的文件&#xff0c;如内核文件和引导加载程序。 /dev&#xff1a;该目录包含了所有设备文件&#xff0c;如硬盘、光驱、鼠标、键盘等等…...

编程日记 2023/9/23 16:42:39

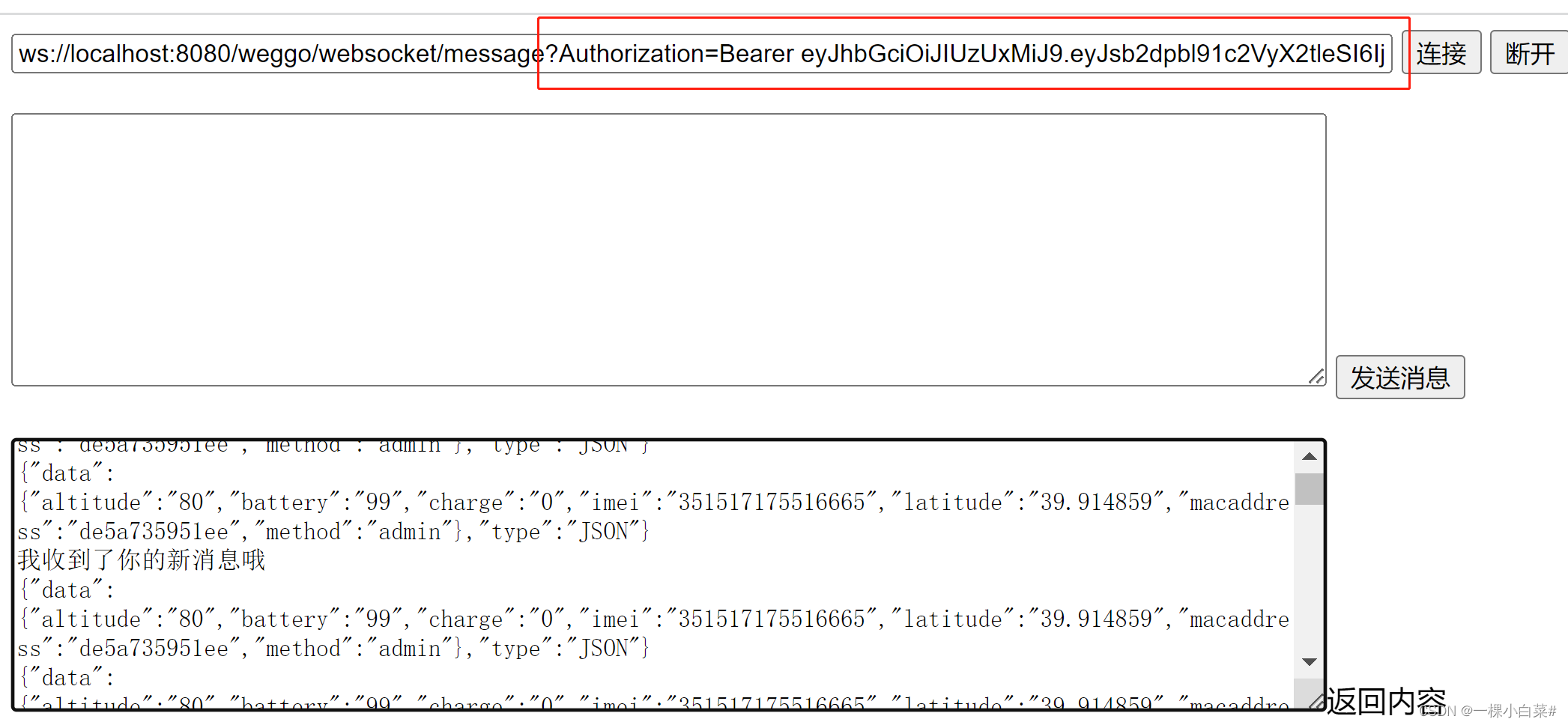
若依框架集成WebSocket带用户信息认证

一、WebSocket 基础知识 我们平时前后台请求用的最多的就是 HTTP/1.1协议&#xff0c;它有一个缺陷&#xff0c; 通信只能由客户端发起&#xff0c;如果想要不断获取服务器信息就要不断轮询发出请求&#xff0c;那么如果我们需要服务器状态变化的时候能够主动通知客户端就需要用…...

编程日记 2023/9/23 16:41:37

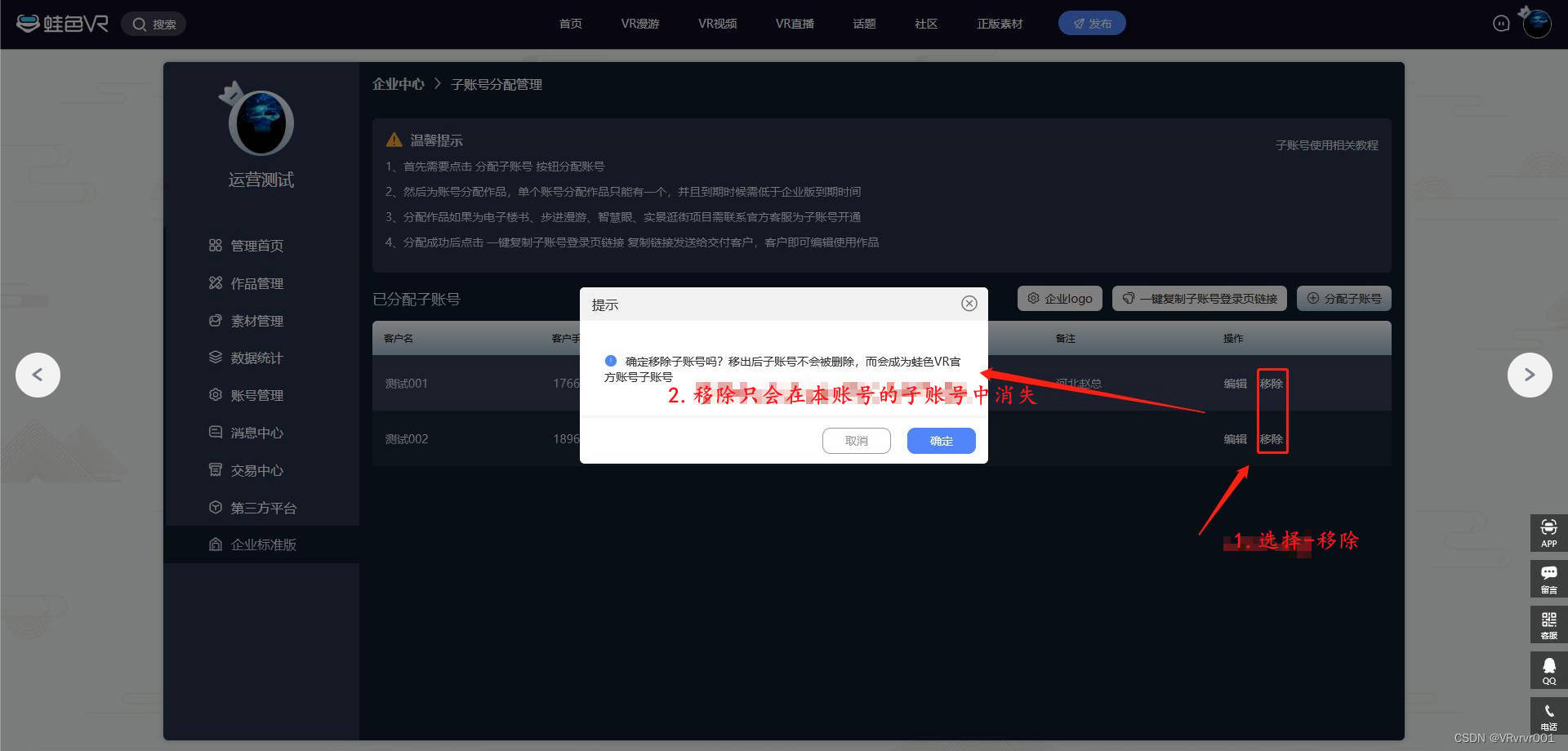
0基础学习VR全景平台篇 第101篇：企业版功能-子账号分配管理

大家好&#xff0c;欢迎观看蛙色VR官方系列——后台使用课程&#xff01; 本期为大家带来蛙色VR平台&#xff0c;企业版教程-子账号分配管理功能&#xff01; 功能位置示意 一、本功能将用在哪里&#xff1f; 子账号分配管理功能&#xff0c;主要用于企业版用户为自己服务的终…...

编程日记 2023/9/23 16:35:29

adb 命令集

adb 查看app启动时间 1.清除时间 adb shell am start -S com.android.systemui/.SystemUIService2.启动应用并记录 adb shell am start -W <PACKAGE_NAME>/.<ACTIVITY_NAME>TotalTime: 491 adb 查看分辨率、dpi 分辨率 adb shell wm sizePhysical size: 1080…...

编程日记 2023/9/23 16:29:21

Golang 面试经典题：map 的 key 可以是什么类型？哪些不可以？

Golang 面试经典题&#xff1a;map 的 key 可以是什么类型&#xff1f;哪些不可以&#xff1f; 在 Golang 的面试中&#xff0c;map 类型的使用是一个常见的考点&#xff0c;其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

编程新知 2025/9/23 20:53:38

Zustand 状态管理库：极简而强大的解决方案

Zustand 是一个轻量级、快速和可扩展的状态管理库&#xff0c;特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

编程新知 2025/12/16 16:47:13

如何在看板中有效管理突发紧急任务

在看板中有效管理突发紧急任务需要&#xff1a;设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP&#xff08;Work-in-Progress&#xff09;弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中&#xff0c;设立专门的紧急任务通道尤为重要&#xff0c;这能…...

编程新知 2025/12/15 20:41:37

Python爬虫（二）：爬虫完整流程

爬虫完整流程详解&#xff08;7大核心步骤实战技巧&#xff09; 一、爬虫完整工作流程 以下是爬虫开发的完整流程&#xff0c;我将结合具体技术点和实战经验展开说明&#xff1a; 1. 目标分析与前期准备 网站技术分析&#xff1a; 使用浏览器开发者工具&#xff08;F12&…...

编程新知 2025/10/19 5:48:51

PAN/FPN

import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

编程新知 2025/10/20 4:39:36

Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换

目录 关键点 技术实现1 技术实现2 摘要&#xff1a; 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式&#xff08;自动驾驶、人工驾驶、远程驾驶、主动安全&#xff09;&#xff0c;并通过实时消息推送更新车…...

编程新知 2025/11/12 0:06:50

Unity UGUI Button事件流程

场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

编程新知 2025/12/17 3:20:13

学习一下用鸿蒙​​DevEco Studio HarmonyOS5实现百度地图

在鸿蒙&#xff08;HarmonyOS5&#xff09;中集成百度地图&#xff0c;可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API&#xff0c;可以构建跨设备的定位、导航和地图展示功能。 ​​1. 鸿蒙环境准备​​ ​​开发工具​​&#xff1a;下载安装 ​​De…...

编程新知 2025/11/13 2:37:01

WEB3全栈开发——面试专业技能点P7前端与链上集成

一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染&#xff08;SSR&#xff09;与静态网站生成&#xff08;SSG&#xff09; 框架&#xff0c;由 Vercel 开发。它简化了构建生产级 React 应用的过程&#xff0c;并内置了很多特性&#xff1a; ✅ 文件系…...

编程新知 2025/11/22 5:40:56

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据（33个指标）

旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据&#xff01;该数据集源自2025年4月发表于《地理学报》的论文成果…...

编程新知 2025/12/9 4:34:27