线性归一化是什么,用python实现数据的线性归一化
线性归一化(Linear Normalization)是一种常见的数据预处理方法,也被称为 Min-Max 归一化。它通过对原始数据进行线性变换,将其缩放到特定的范围内,常用的是将数据缩放到 [0, 1] 或 [-1, 1] 范围内。
具体来说,对于原始数据 X X X,它的线性归一化可以表示为:
X n o r m = X − X m i n X m a x − X m i n X_{norm} = \frac{X - X_{min}}{X_{max} - X_{min}} Xnorm=Xmax−XminX−Xmin
其中, X m i n X_{min} Xmin 和 X m a x X_{max} Xmax 分别表示原始数据中的最小值和最大值。通过这个公式,将原始数据 X X X 缩放到 [ 0 , 1 ] [0, 1] [0,1] 的区间内,使得新的归一化后的数据 X n o r m X_{norm} Xnorm 满足 0 ≤ X n o r m ≤ 1 0 \leq X_{norm} \leq 1 0≤Xnorm≤1。
需要注意的是,线性归一化假设数据的分布是均匀分布的,并且对于极端值比较敏感,可能会受到异常值的影响。因此,在使用线性归一化进行数据预处理时,需要针对具体问题进行评估,并考虑其他数据预处理方法的使用。
python实现
在Python中,可以使用NumPy库来实现数据的线性归一化。下面是一个简单的示例代码:
import numpy as npdef linear_normalization(data):# 计算最大值和最小值min_val = np.min(data)max_val = np.max(data)# 线性归一化normalized_data = (data - min_val) / (max_val - min_val)return normalized_data# 示例数据
data = np.array([1, 2, 3, 4, 5])# 线性归一化
normalized_data = linear_normalization(data)print(normalized_data)
运行以上代码,将输出归一化后的数据 [0. 0.25 0.5 0.75 1. ]。
在上述代码中,linear_normalization 函数接受一个包含原始数据的NumPy数组作为输入,使用 np.min() 和 np.max() 函数分别计算数据的最小值和最大值。然后,通过 (data - min_val) / (max_val - min_val) 进行线性归一化计算,得到归一化后的数据 normalized_data,并将其返回。
注意,在实际应用中,可能需要对数据进行处理,例如转换成浮点数类型或处理多维数据。此外,如果数据集很大,也可以考虑使用更高效的方法来计算最小值和最大值,以提高计算速度。
相关文章:

线性归一化是什么,用python实现数据的线性归一化
线性归一化(Linear Normalization)是一种常见的数据预处理方法,也被称为 Min-Max 归一化。它通过对原始数据进行线性变换,将其缩放到特定的范围内,常用的是将数据缩放到 [0, 1] 或 [-1, 1] 范围内。 具体来说ÿ…...
超级好用绘图工具(Draw.io+Github)
超级好用绘图工具(Draw.ioGithub) 方案简介 绘图工具:Draw.io 存储方式: Github 1 Draw.io 1.2 简介 是一款免费开源的在线流程图绘制软件,可以用于创建流程图、组织结构图、网络图、UML图等各种类型的图表。…...
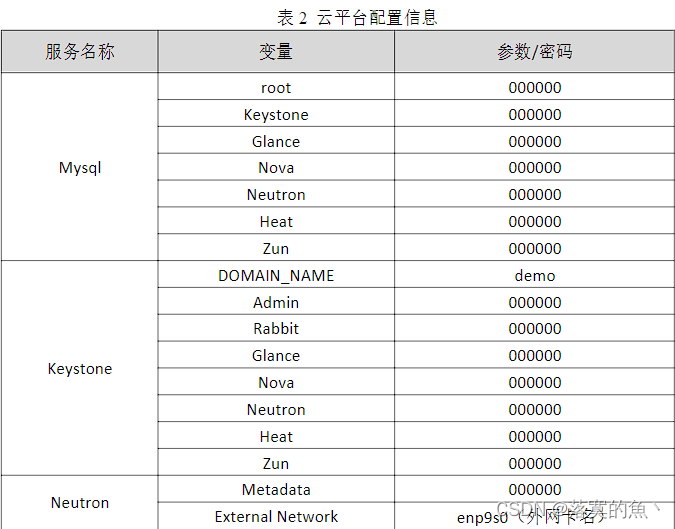
全国职业技能大赛云计算--高职组赛题卷③(私有云)
全国职业技能大赛云计算--高职组赛题卷③(私有云) 第一场次题目:OpenStack平台部署与运维任务1 基础运维任务(5分)任务2 OpenStack搭建任务(15分)任务3 OpenStack云平台运维(15分&am…...
)
Redis SCAN命令操作实战(详细)
目录 SCAN 介绍 SCAN 命令基本用法 MATCH 选项用法 COUNT 选项用法 TYPE 选项用法 补充 并发执行多个迭代 中途停止迭代 使用错误的游标进行增量式迭代 迭代终结的保证 SCAN 介绍 SCAN cursor [MATCH pattern] [COUNT count][TYPE type]:SCAN 命令及其相…...
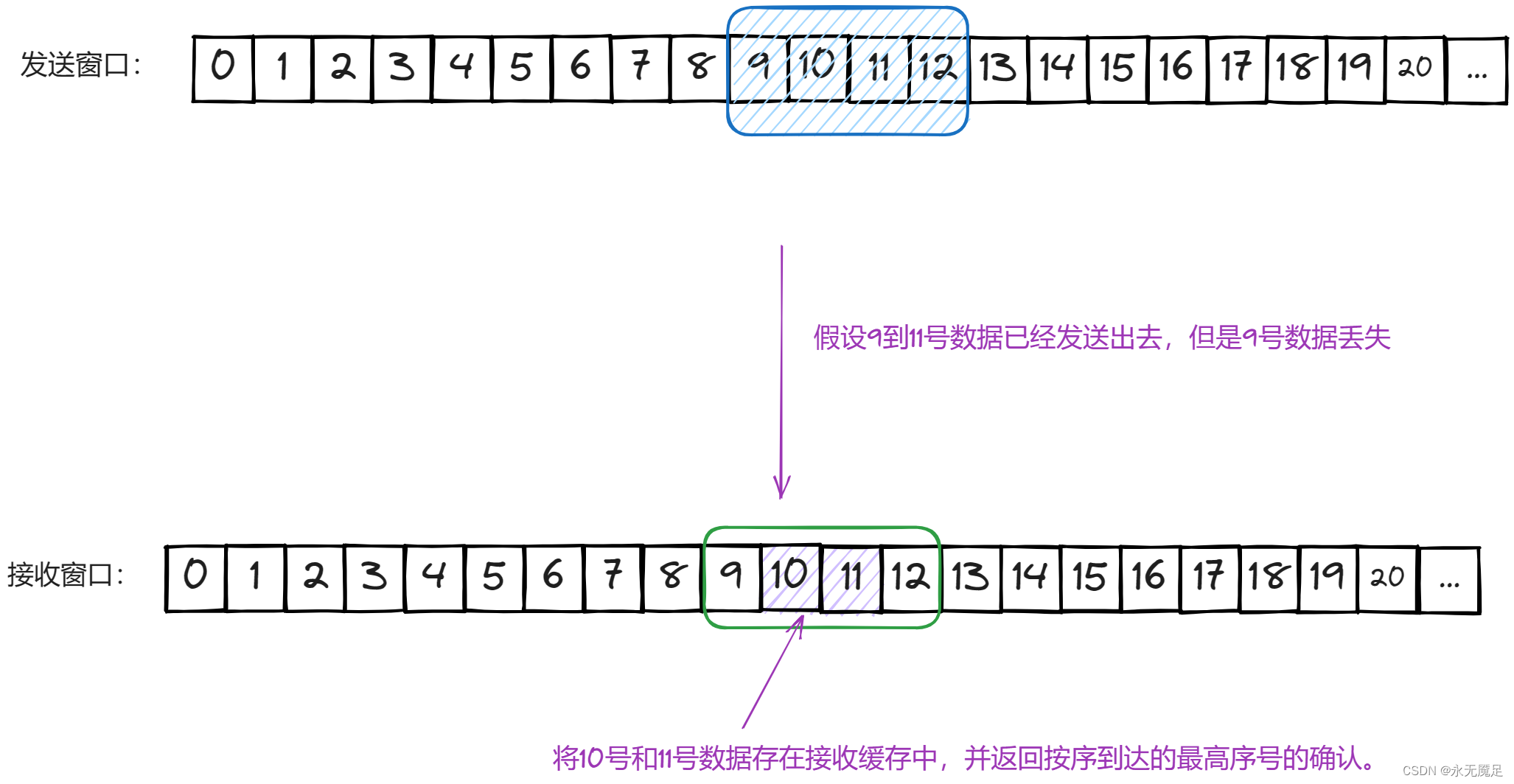
计网第五章(运输层)(六)(TCP可靠传输的实现)
目录 一、基本概述 二、具体实现 1.前后沿: 2.利用指针描述发送窗口的状态 3.有差错情况 之前在数据链路层时已经讨论过可靠传输(计网第三章(数据链路层)(二)(可靠传输)&#x…...
酒店外卖小程序商城的作用是什么
随着线上餐品销售属性增强,传统酒店除了承接到店客户,外送也成为生意的一部分,但传统打电话、微信发送的方式无法实现餐品全面呈现和客户随时订购需求,在配送方面也无法规范化。 除此之外,还需要完善营销、会员管理、…...

居家养老一键通的功能
居家养老一键通的功能 居家养老一键通是指为老年人提供全方位的居家养老服务的平台或系统。它通过整合各种资源和服务,为老年人提供便捷、安全、舒适的居家养老环境,帮助他们解决生活中的各种难题。 居家养老一键通的功能通常包括以下几个方面ÿ…...
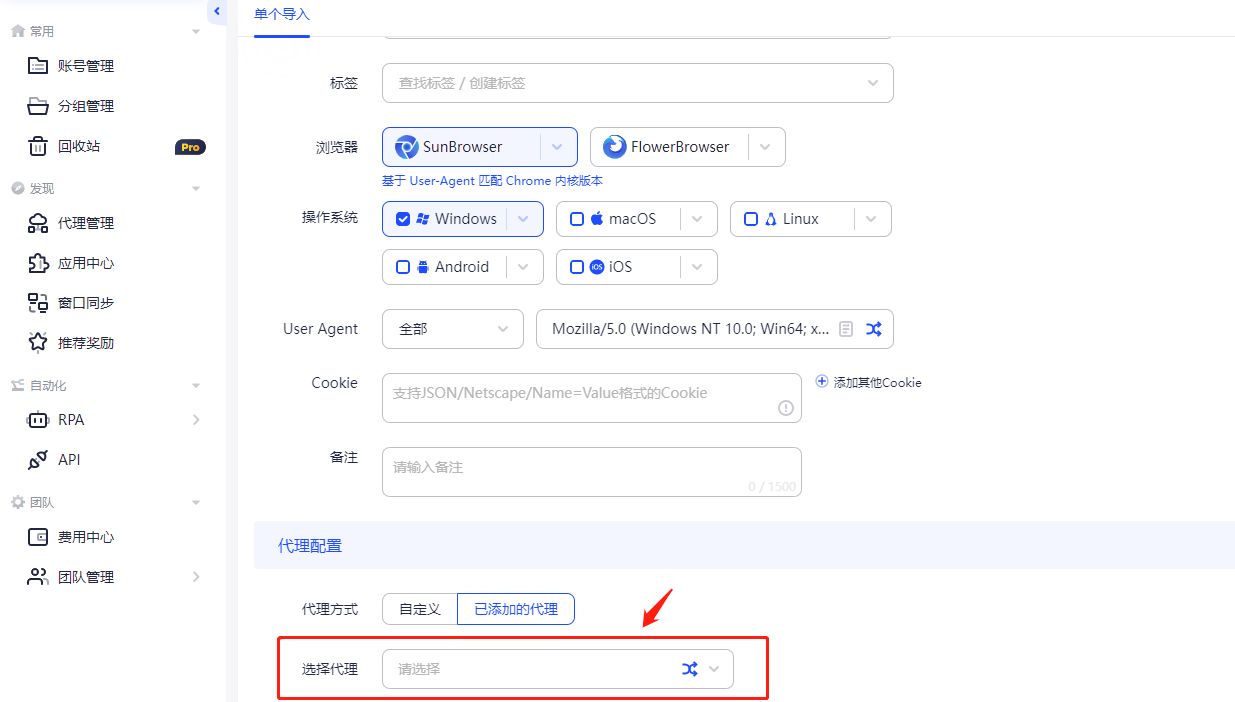
海外代理IP是什么?如何使用?
一、海外代理IP是什么? 首先,代理服务器是在用户和互联网之间提供网关的系统或路由器。它是一个服务器,被称为“中介”,因为它位于最终用户和他们在线访问的网页之间。 海外IP代理是就是指从海外地区获取的IP地址,用…...

mmdetection v3避坑
命令: python tools/test.py projects/DiffusionDet/configs/diffusiondet_r50_fpn_500-proposals_1-step_crop-ms-480-800-450k_coco.py /data/zhangrui/mmdetection-master/checkpoints/diffusiondet_r50_fpn_500-proposals_1-step_crop-ms-480-800-450k_coco_202…...

备份服务器数据库并保存到Git仓库
备份项目及数据库脚本 #!/bin/bash # MySQL数据库信息 DB_HOST"localhost" DB_USER"root" DB_PASS"************" DB_NAME"my-space" # 导出文件目录 EXPORT_PATH"/home/MySpace/mysql" # 获取当前时间并格式…...
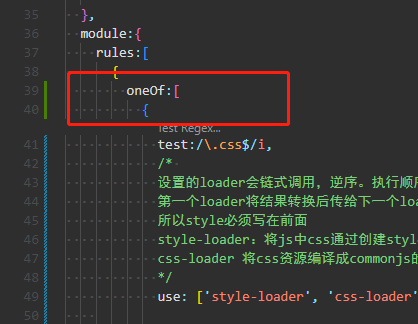
尚硅谷wepack课程学习笔记
为什么需要使用打包工具? 开发时使用的框架、es6 语法 、less 等浏览器无法识别。 需要经过编译成浏览器能识别的css、js才可以运行。 打包工具可以帮我们编译,号可以做代码压缩、兼容处理、性能优化。 常见的打包工具有什么? vite、webpac…...

c++模版元编程-可变参数模版
在 C 中,我们可以使用模板参数包(Template Parameter Pack)和展开表达式(Expanding Expression)来定义可变参数模板。 模板参数包 模板参数包是一种特殊的语法,用于表示接受多个模板类型参数或非类型参数…...

pcl--第十节 点云曲面重建
曲面重建技术在逆向工程、数据可视化、机器视觉、虚拟现实、医疗技术等领域中得到了广泛的应用 。 例如,在汽车、航空等工业领域中,复杂外形产品的设计仍需要根据手工模型,采用逆向工程的手段建立产品的数字化模型,根据测量数据建…...

【力扣-每日一题】2560. 打家劫舍 IV
class Solution { public:bool check(vector<int> &nums,int max_num,int k){//只需要计算可以偷的房间。在满足最大值为max_num下时,能偷的最多的房间,与k值比较//如果大于K,说明max_num还可以缩小//如果小于看,说明ma…...
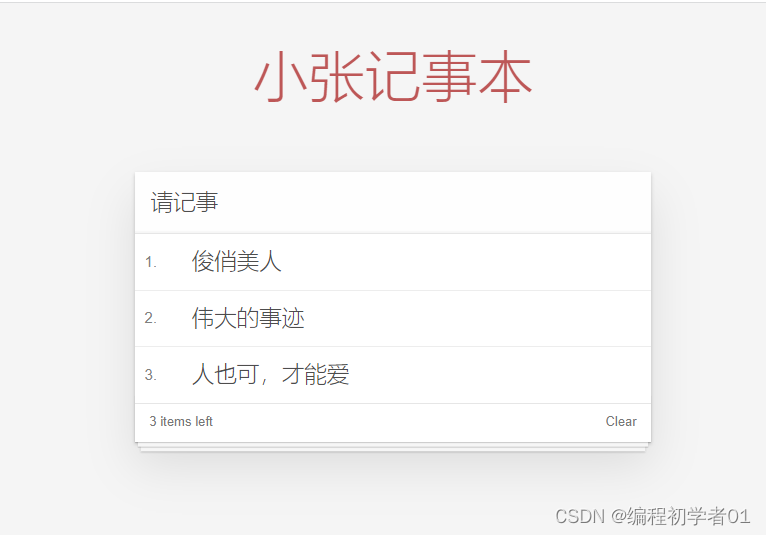
vue简单案例----小张记事本
小张记事本 具体效果如图所示,这里就简单展示,还有很多不足的地方,希望大家可以对这个小项目进行改进,话不多说可以参考下面的代码 源代码如下 <html lang"en"><head><meta charset"UTF-8"…...
爬虫获取接口数据
上一讲讲的是获取静态网页数据的教程,适用于我们要爬取的数据在网页源代码中出现,但是还是有很多的数据是源代码中没有的,需要通过接口访问服务器来获得,下面我就来讲讲如何爬取这类数据。 以巨潮资讯网爬取比亚迪企业年报为例。…...

私域流量的变现方式,你知道多少?
私域流量的变现方式是指通过有效的管理和运营自有的用户群体,将流量转化为实际收益的过程。私域流量的变现方式多样,下面将介绍其中几种常见的方式。 1. 电商平台入驻 通过将自有流量引导到电商平台,开设店铺进行商品销售,从中获…...
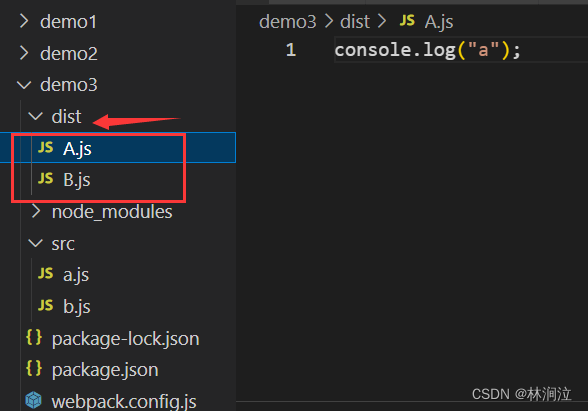
Webpack配置entry修改入口文件或打包多个文件
当我们使用Webpack进行文件打包时,默认打包的文件是src文件下的index.js文件 一、修改Webpack打包入口 如果我们想要在其他文件下打包指定的js文件就需要在webpack.config.js文件中进行entry配置 二、将指定的多个文件打包为一个文件 现在有两个文件,…...
重装回MacOS)
Mac mini2014(装的windows)重装回MacOS
Mac mini2014(装的windows)重装回MacOS 制作macos的启动U盘,我的是32G的 第一步下载你的硬件能使用的系统,建议最好低一个版本,因为我安装的时候出现问题。 下载地址:https://blog.csdn.net/netgc/article/details/130641479下载…...

珠海建筑模板厂家-能强优品木业:为您提供优质建筑模板解决方案
在珠海这座美丽的沿海城市,建筑行业蓬勃发展,对于高质量的建筑模板需求也日益增加。在这里,有一家备受赞誉的建筑模板厂家,那就是能强优品木业。作为一家专业的建筑模板供应商,他们以优质的产品和卓越的服务在业界享有…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
