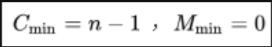八大排序(一)冒泡排序,选择排序,插入排序,希尔排序
一、冒泡排序
冒泡排序的原理是:从左到右,相邻元素进行比较。每次比较一轮,就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。
以从小到大排序为例,第一轮比较后,所有数中最大的那个数就会浮到最右边;第二轮比较后,所有数中第二大的那个数就会浮到倒数第二个位置……就这样一轮一轮地比较,最后实现从小到大排序。
代码如下:
void BubbleSort(int* a, int n)
{for (size_t j = 0; j < n; j++){int exchange = 0;for (size_t i = 1; i < n-j; i++){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}}
}冒泡排序时间复杂度
如果待排序序列的初始状态恰好是我们希望的排序结果(如升序或降序),一趟扫描即可完成排序。
所需的关键字比较次数C和记录移动次数M均达到最小值:
冒泡排序最好的时间复杂度为O(n)。
如果待排序序列是反序(如我们希望的结果是升序,待排序序列是降序)的,需要进行n-1趟排序。每趟排序要进行n-i次关键字的比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:
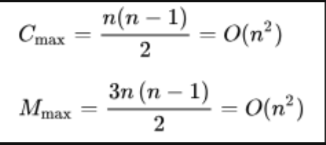
冒泡排序的最坏时间复杂度为O(N^2)
综上,因此冒泡排序总的平均时间复杂度为O(N^2)冒泡排序是稳定的排序
二、选择排序
选择排序的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,继续放在起始位置知道未排序元素个数为0。
选择排序的步骤:
1>首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
2>再从剩余未排序元素中继续寻找最小(大)元素,然后放到未排序序列的起始位置。
3>重复第二步,直到所有元素均排序完毕。
选择排序代码实现:
//交换两个数据
void Swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}//选择排序
void SelectSort(int* arr, int size)
{int i = 0;for (i = 0; i < size-1; i++){int min = i;int j = 0;for (j = i+1; j < size; j++){if (arr[j] < arr[min]){min = j;}}Swap(&arr[i], &arr[min]);}
}
思路优化:
以上算法是每次找出最小的放在指定位置,一共要找n-1次,如果我们每次不但找到最小的,还找到最大的,将最小的与左端交换,最大的与右端交换,那么就少了一半的遍历次数,从而提高效率。
- 变量
begin和变量end是数组的两端,min和max分别找小和大的下标- 先交换
min与begin位置的数值,再交换max与end位置的数值begin右移,end左移,继续找大找小,继续交换- 重复上述操作,直到遍历完所有数组
排序优化后问题
若是max的位置与begin重合,则begin先与min的位置交换,此时max位置的最大值被交换走,导致end与max交换的数值是错误的。
问题解决:
当max与begin重合时,begin与min交换后导致max指向的不再是最大值,所以当我们对begin交换后,就要对max进行一个修正,让max指向最大值,然后完成end的交换
1、max与
begin重合,并且begin此时完成了交换,此时最大值已经交换到了min所指向的位置2、对
max进行修正并完成与end的交换
优化后代码:
//交换两个数据
void Swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}//选择排序
void SelectSort(int* arr, int size)
{int begin = 0;int end = size - 1;while (begin < end){int max = begin;int min = begin;int i = 0;for (i = begin+1; i <= end; i++){if (arr[i] < arr[min]){min = i;}if (arr[i] > arr[max]){max = i;}}Swap(&arr[begin], &arr[min]);if (begin == max) //修正max{max = min;}Swap(&arr[end], &arr[max]);begin++;end--;}
}
选择排序时间复杂度:
时间复杂度:O(n^2)
空间复杂度:O ( 1 )
选择排序是不稳定的排序
三、插入排序
直接插入排序是一种简单的插入排序法,对数组进行一个遍历,每次都对待排的数据按照大小顺序插入到一个有序数组中的特定位置,直到所有的数据全部插入完毕,就得到一个有序数列。
插入排序的算法非常简单,依次对每一个元素进行单趟排序就行了,由于要前一个数比较则只需要从1开始遍历n-1次

当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的
元素顺序后移
插入排序代码:
void InsertSort(int* arr, int size)
{int i = 0;for (i = 1; i < size; i++){int end = i;int temp = arr[end]; //记录待排数值while (end > 0){if (arr[end-1] > temp) //若前一个数大于待排数值,则后移一位{arr[end] = arr[end-1];end--;}else{break;}}// arr[end-1] = temp;是之前的错误,现已修正arr[end] = temp; //将数据放入插入位置}
}
插入排序的时间复杂度:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
四、希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
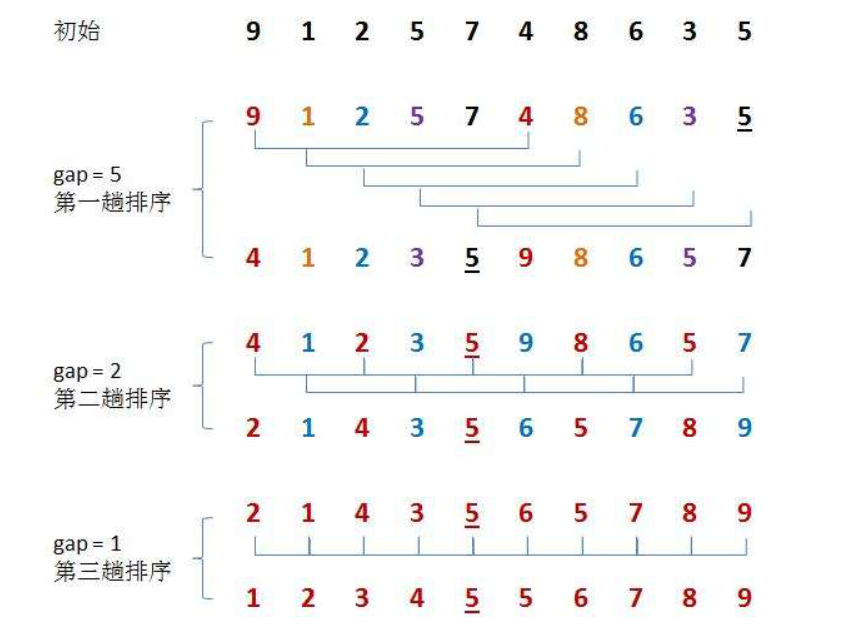
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
3. 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
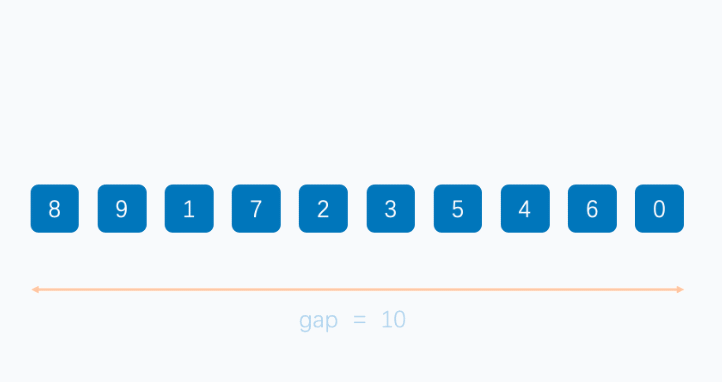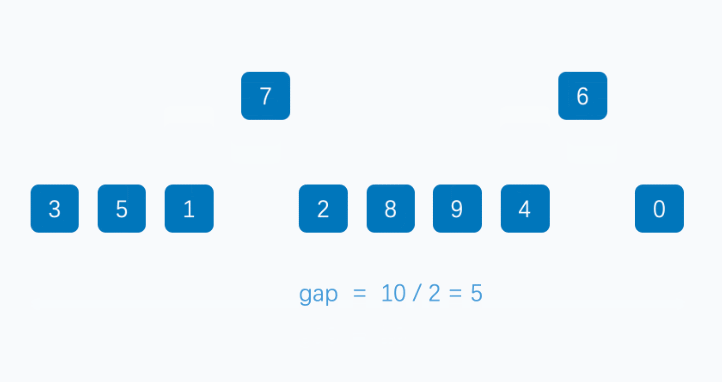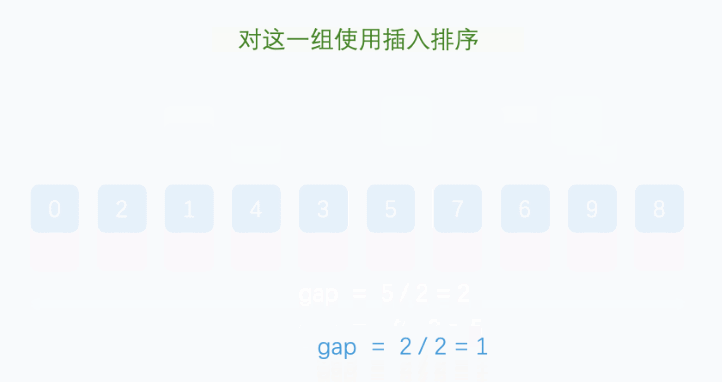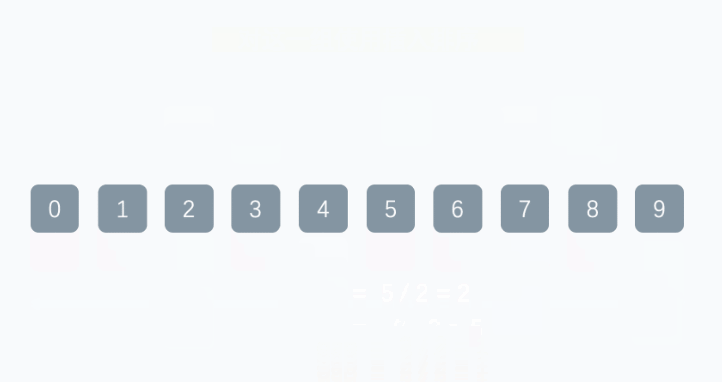
希尔排序代码实现:
void ShellSort(int* arr, int size)
{int gap = size;while (gap > 1){gap = gap / 2; //调整希尔增量int i = 0;for (i = 0; i < size - gap; i++) //从0遍历到size-gap-1{int end = i;int temp = arr[end + gap];while (end >= 0){if (arr[end] > temp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = temp; //以 end+gap 作为插入位置}}
}
希尔排序的时间复杂度:
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些书中给出的希尔排序的时间复杂度都不固定:
时间复杂度:O(n^1.3)
稳定性:不稳定
相关文章:

八大排序(一)冒泡排序,选择排序,插入排序,希尔排序
一、冒泡排序 冒泡排序的原理是:从左到右,相邻元素进行比较。每次比较一轮,就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。 以从小到大排序为例,第一轮比较后,所有数中最大的那个数就会浮…...

泊松分布简要介绍
泊松分布是一种常见的离散概率分布,它用于描述某个时间段或区域内随机事件发生的次数。它得名于法国数学家西蒙丹尼泊松。 泊松分布的概率质量函数表示某个时间段或区域内事件发生次数的概率。如果随机变量 X 服从泊松分布,记作 X ~ Poisson(λ)&#x…...

C语言每日一题(10):无人生还
文章主题:无人生还🔥所属专栏:C语言每日一题📗作者简介:每天不定时更新C语言的小白一枚,记录分享自己每天的所思所想😄🎶个人主页:[₽]的个人主页🏄…...

VSCode开发go手记
断点调试: 安装delve(windows): go get -u github.com/go-delve/delve/cmd/dlv 设置 launch.json 配置文件: ctrlshiftp 输入 Debug: Open launch.json 打开 launch.json 文件,如果第一次打开,会新建一…...

怎么选择AI伪原创工具-AI伪原创工具有哪些
在数字时代,创作和发布内容已经成为了一种不可或缺的活动。不论您是个人博主、企业家还是网站管理员,都会面临一个共同的挑战:如何在互联网上脱颖而出,吸引更多的读者和访客。而正是在这个背景下,AI伪原创工具逐渐崭露…...

【块状链表C++】文本编辑器(指针中 引用 的使用)
》》》算法竞赛 /*** file * author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * brief 一直在竞赛算法学习的路上* * copyright 2023.9* COPYRIGHT 原创技术笔记:转载…...
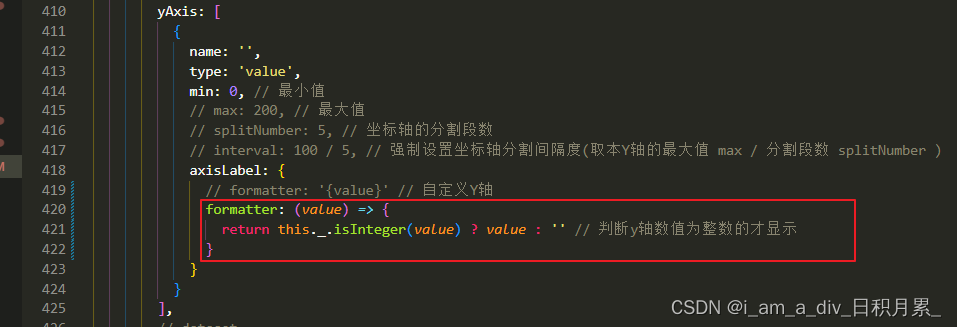
echarts的Y轴设置为整数
场景:使用echarts,设置Y轴为整数。通过判断Y轴的数值为整数才显示即可 yAxis: [{name: ,type: value,min: 0, // 最小值// max: 200, // 最大值// splitNumber: 5, // 坐标轴的分割段数// interval: 100 / 5, // 强制设置坐标轴分割间隔度(取本Y轴的最大…...
恢复删除文件?不得不掌握的4个方法!
“删除了的文件还可以恢复吗?有个文件我本来以为不重要了,就把它删除了,没想到现在还需要用到!这可怎么办?有没有办法找回来呢?” 重要的文件一旦丢失或误删可能都会对我们的工作和学习造成比较大的影响。怎…...

GitLab CI/CD:.gitlab-ci.yml 文件常用参数小结
文章目录 一、.gitlab-ci.yml 文件作用二、一个简单的.gitlab-ci.yml 文件示例参考 一、.gitlab-ci.yml 文件作用 可以定义跑CI时想要运行的命令或脚本 可以定义job之间的依赖和缓存 可以执行程序部署并定义部署位置 可以定义想要包含的其他配置文件和模版 二、一个简单的.gi…...
MySQL学习笔记9
MySQL数据表中的数据类型: 在考虑数据类型、长度、标度和精度时,一定要仔细地进行短期和长远的规划,另外,公司制度和希望用户用什么方式访问数据也是要考虑的因素。开发人员应该了解数据的本质,以及数据在数据库里是如…...

从零学习开发一个RISC-V操作系统(三)丨嵌入式操作系统开发的常用概念和工具
本篇文章的内容 一、嵌入式操作习系统开发的常用概念和工具1.1 本地编译和交叉编译1.2 调试器GDB(The GNU Project Debugger)1.3 QEMU模拟器1.4 项目构造工具Make 本系列是博主参考B站课程学习开发一个RISC-V的操作系统的学习笔记,计划从RISC…...
小米机型解锁bl 跳“168小时”限制 操作步骤分析
写到前面的安全提示 了解解锁bl后的风险: 解锁设备后将允许修改系统重要组件,并有可能在一定程度上导致设备受损;解锁后设备安全性将失去保证,易受恶意软件攻击,从而导致个人隐私数据泄露;解锁后部分对系…...

基础练习 回文数
问题描述 1221是一个非常特殊的数,它从左边读和从右边读是一样的,编程求所有这样的四位十进制数。 输出格式 按从小到大的顺序输出满足条件的四位十进制数。 solution1 #include <stdio.h> int main(){int n 1000, n1, n2, n3, n4;while(n &…...

解决Spring Boot 2.7.16 在服务器显示启动成功无法访问问题:从本地到服务器的部署坑
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

洛谷P5661:公交换乘 ← CSP-J 2019 复赛第2题
【题目来源】https://www.luogu.com.cn/problem/P5661https://www.acwing.com/problem/content/1164/【题目描述】 著名旅游城市 B 市为了鼓励大家采用公共交通方式出行,推出了一种地铁换乘公交车的优惠方案: 1.在搭乘一次地铁后可以获得一张优惠票&…...

mysql优化之索引
索引官方定义:索引是帮助mysql高效获取数据的数据结构。 索引的目的在于提高查询效率,可以类比字典。 可以简单理解为:排好序的快速查找数据结构 在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这种数据…...
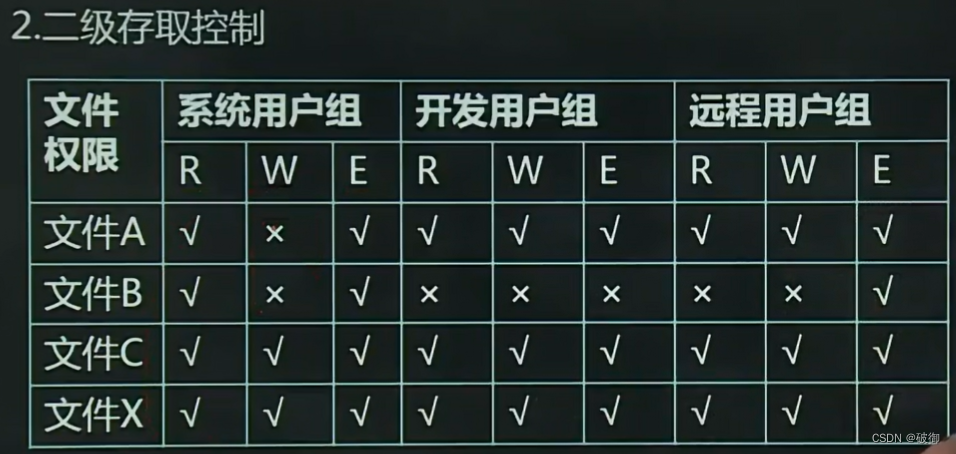
文件系统详解
目录 文件系统(1) 第一节文件系统的基本概念 一、文件系统的任务 二、文件的存储介质及存储方式 三、文件的分类 第二节 文件的逻辑结构和物理结构 一、文件的逻辑结构 二、文件的物理结构 文件系统(2) 第三节 文件目…...

有名管道及其应用
创建FIFO文件 1.通过命令: mkfifo 文件名 2.通过函数: mkfifo #include <sys/types.h> #include <sys/stat.h> int mkfifo(const char *pathname, mode_t mode); 参数: -pathname:管道名称的路径 -mode:文件的权限&a…...

加州大学伯克利分校 计算机科学专业
加州大学伯克利分校 计算机科学专业 cs 61a cs 61b cs61c...
一个关于 i++ 和 ++i 的面试题打趴了所有人
前言 都说大城市现在不好找工作,可小城市却也不好招人。 我们公司招了挺久都没招到,主管感到有些心累。 我提了点建议,是不是面试问的太深了,在这种小城市,能干活就行。 他说自己问的面试题都很浅显,如果答…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...