概率论几种易混淆的形式
- 正态分布标准型
x − μ σ \frac{x - \mu}{\sigma} σx−μ
- 大数定律形式
P { X ≤ ∑ i = 1 n x i − n μ n σ 2 } = ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\sum_{i= 1}^{n}x_i -n\mu}{\sqrt{n\sigma^2}} \} = \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx P{X≤nσ2∑i=1nxi−nμ}=∫−∞X2π1e−2x2dx
即:
P { X ≤ x ˉ − μ σ n } = ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\bar x -\mu}{\frac{\sigma}{\sqrt{n}}} \} = \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx P{X≤nσxˉ−μ}=∫−∞X2π1e−2x2dx
- 关于 χ 2 \chi^2 χ2的定理
( n − 1 ) S 2 σ 2 ∼ χ 2 ( n − 1 ) \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) σ2(n−1)S2∼χ2(n−1)
- x ˉ − μ S / n ∼ t 2 ( n − 1 ) \frac{\bar x - \mu}{S/\sqrt{n}} \sim t^2(n-1) S/nxˉ−μ∼t2(n−1)
相关文章:

概率论几种易混淆的形式
正态分布标准型 x − μ σ \frac{x - \mu}{\sigma} σx−μ 大数定律形式 P { X ≤ ∑ i 1 n x i − n μ n σ 2 } ∫ − ∞ X 1 2 π e − x 2 2 d x P\{X \le \frac{\sum_{i 1}^{n}x_i -n\mu}{\sqrt{n\sigma^2}} \} \int _{-\infty}^{X}\frac{1}{\sqrt{2\pi}}e^{-\fr…...

PyTorch数据增强后的结果展示
from PIL import Image import torch from torchvision import transformstrans transforms.Compose([transforms.ToTensor(), transforms.RandomErasing(p0.9, value 120, inplaceTrue)]) # 这里Compose是所做的变换img_path 02-56-45-060-1454-camra1.bmp img Image.open…...

指定程序在哪个GPU上运行
摘要: 当本地(或服务器)有个多个GPU时,需要指定程序在指定GPU上运行,需要做以下设置。 目录 一、在终端上指定GPU二、在程序中指定GPU三、系统变量指定GPU四、pytorch中指定GPU 一、在终端上指定GPU 在终端运行程序时…...

Linux CentOS7 vim多文件编辑
使用vim编辑多个文件,十分常用的操作。本文从打开、显示、切换文件到退出,进行简单讨论。 一、打开文件 1.一次打开多个文件 vim还没有启动的时候,在终端里输入vim file1 file2 … filen便可以打开所有想要打开的文件。 执行命令 vim fil…...

PAT甲级真题1153: 解码PAT准考证
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux菜鸟刷题集 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的…...

linux信号
title: linux信号 createTime: 2020-10-29 18:05:52 updateTime: 2020-10-29 18:05:52 categories: linux tags: SIGHUP 终止进程 终端线路挂断[喝小酒的网摘]http://blog.hehehehehe.cn/a/16999.htm SIGINT 终止进程 中断进程 SIGQUIT 建立CORE文件终止进程,并且生…...

JavaWeb开发-05-SpringBootWeb请求响应
一.请求 1.Postman 2.简单参数 package com.wjh.controller;import org.springframework.web.bind.annotation.RequestMapping; import org.springframework.web.bind.annotation.RestController;import javax.servlet.http.HttpServletRequest;/** 测试请求参数接受*/ R…...

Ubuntu下载
参考文档: 镜像文件:VMware下安装ubuntu 16.04(全步骤)_vmwaubuntu-16.04.4-desktop-amd64.iso_ST0new的博客-CSDN博客 vmware tools使用安装:VMware——VMware Tools的介绍及安装方法_William.csj的博客-CSDN博客 …...

Vue 的组件加载顺序和渲染顺序
1、结论先行 组件的加载顺序是自上而下的,也就是先加载父组件,再递归地加载其所有的子组件。 而组件渲染顺序是按照深度优先遍历的方式,也就是先渲染最深层的子组件,再依次向上渲染其父组件。 2、案例 下面是一个简单的示例代…...
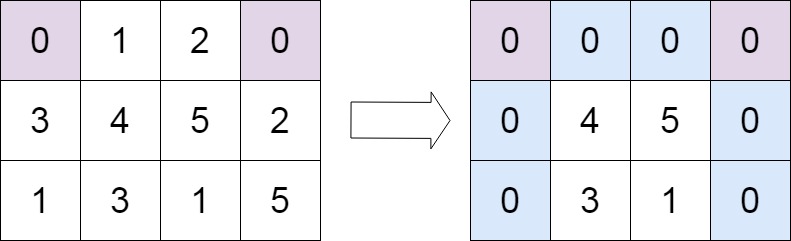
leetcode Top100(17)矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2: 输入&…...
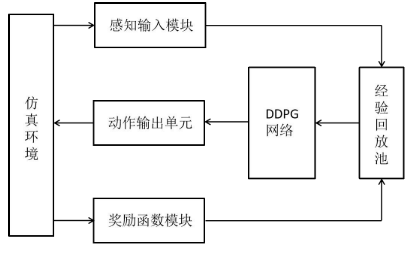
论文精读(2)—基于稀疏奖励强化学习的机械臂运动规划算法设计与实现(内含实现机器人控制的方法)
目录 1.作者提出的问题及解决方向 2.延深-用如何用强化学习对机器人进行控制 2.1思路 2.2DQN和DDPG在机器人控制中的应用 3.解决方案 3.1思路 3.2实验 3.3创新点 4.展望 1.作者提出的问题及解决方向 目的:使机械臂在非结构化环境下实现端到端的自主学习控制…...

快速安装keepalive
快速安装keepalive #安装 yum install keepalived -y# 查看版本: rpm -q -a keepalived#修改配置文件 vim /etc/keepalived.conf虚拟 ip :随意选一个,不被占用的ip即可。...
nginx实现反向代理实例
1 前言 1.1 演示内容 在服务器上访问nginx端口然后跳转到tomcat服务器 1.2 前提条件 前提条件:利用docker安装好nginx、tomcat、jdk8(tomcat运行需要jdk环境) 只演示docker安装tomcat: 默认拉取最新版tomcat docker pull t…...

使用Freemarker填充模板导出复杂Excel,其实很简单哒!
文章目录 1. 需求分析2. 对象生成3. 列表插值4. 另存xml格式化5. ftl修改6. 程序转化7. 犯的错误8. 总结 1. 需求分析 类似这样的一个表格 我们需要从数据库中查询对应的数据,将其汇总进该表格,并且可能还需要复制表格项,我这个案例中没有&a…...

windows环境下安装logstash同步数据,注册系统服务
windows环境下安装logstash同步数据,注册系统服务 此方法适用于Windows环境,同一个配置文件配置多个管道,并且配置系统服务,防止程序被杀进程 一、安装logstash (1)下载压缩包,解压后修改con…...
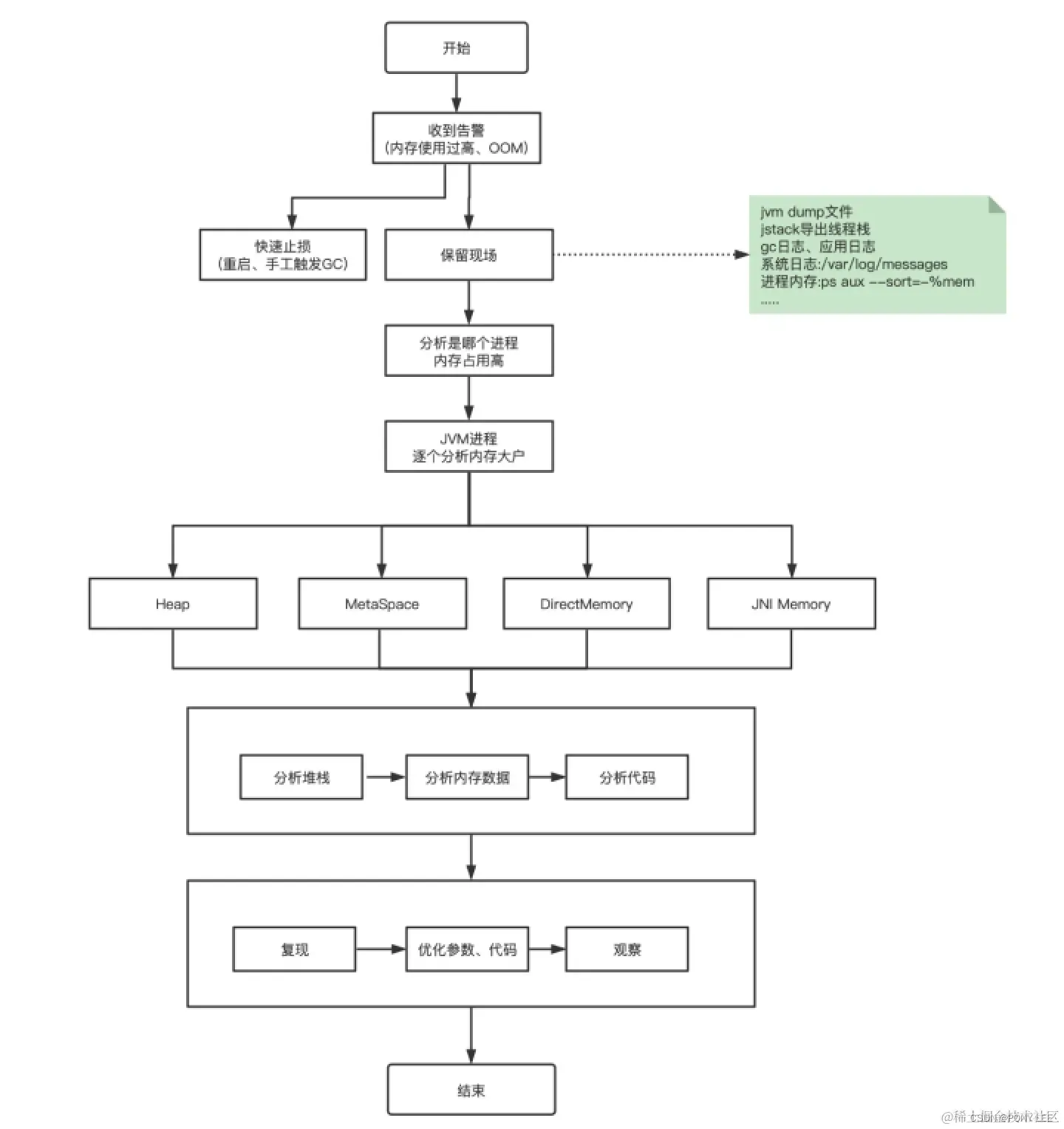
java服务内存说明及配置详解
java进程内存 JVM内存分布图: 【java进程内存】【堆外内存】 【jvm堆内存】 【堆外内存】 【Metaspace】 【Direct Memory】【JNI Memory】【code_cache】 … 堆外内存泄漏的排查在于【本地内存(Native Memory)】【Direct Memory】【JNI Memory】 一般…...
Mybatis-MyBatis的缓存
Mybatis-MyBatis的缓存 一、MyBatis的一级缓存二、MyBatis的二级缓存二级缓存的相关配置 三、MyBatis缓存查询的顺序 一、MyBatis的一级缓存 一级缓存是SqlSession级别的,通过同一个SqlSession查询的数据会被缓存,下次查询相同的数据,就 会从…...
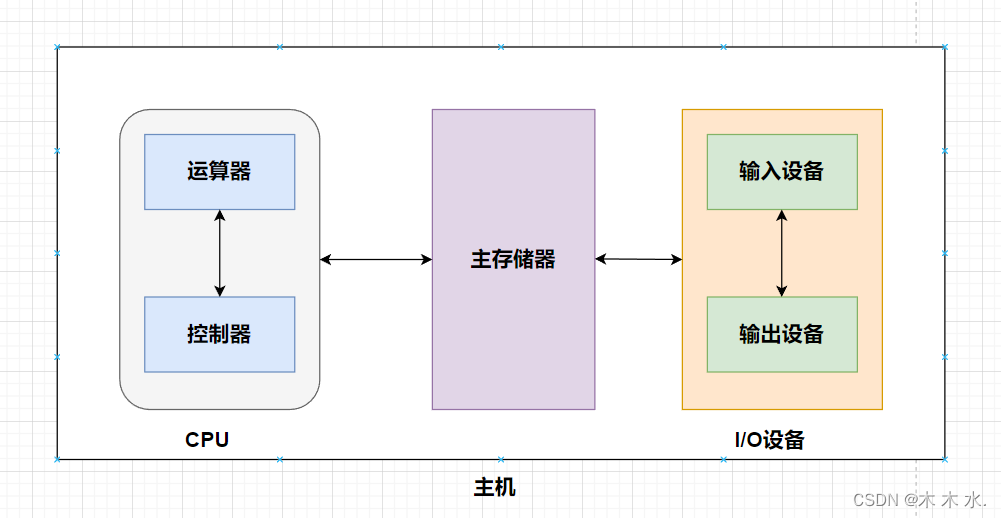
计算机组成原理之硬件的基本组成,深入介绍两大计算机结构体系,从底层出发认识计算机。
大家好,欢迎阅读《计算机组成原理》的系列文章,本系列文章主要的内容是从零学习计算机组成原理,内容通俗易懂,大家好好学习吧!!! 更多的优质内容,请点击以下链接查看哦~~ ↓ ↓ ↓ …...
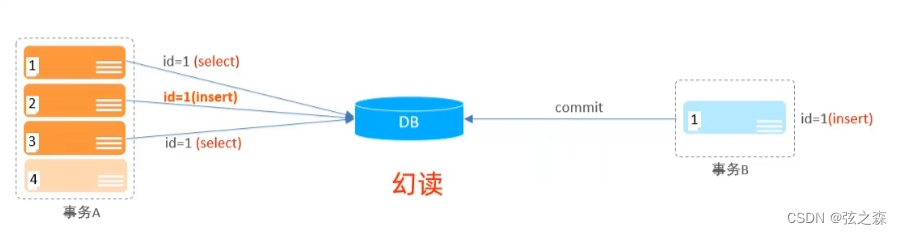
二十五、MySQL事务的四大特性和常见的并发事务问题
1、事务的四大特性 2、常见的并发事务问题 (1)并发事务问题分类: (2)脏读: 一个事务正在对一条记录做修改,在这个事务完成并提交前,这条记录的数据就处于不一致的状态;…...
辨析常见的医学数据分析(相关性分析回归分析)
目录 1 常见的三种分类结果? 2 什么是相关性分析? 相关性分析的结果怎么看? 3 什么是回归分析? 1)前提 2)常见的回归模型 4 对于存在对照组实验的医学病例如何分析? 1)卡方检验…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
