李航老师《统计学习方法》第五章阅读笔记
决策树(decision tree)是一种基本的分类与回归方法。本章主要讨论用于分类的决策树。决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。
以下是关于分类决策树的一些基本概念和特点:
- 树形结构:决策树模型呈现为一种树状结构,其中包括根节点、内部节点和叶子节点。每个节点表示一个特征或属性,每个边表示一个特征值或属性值的判断条件。从根节点开始,通过遵循不同的条件路径,最终到达叶子节点,叶子节点代表了一个类别标签或回归值。
- if-then规则:决策树可以看作是一组if-then规则的集合,每个规则表示一个从根节点到叶子节点的路径,其中包括特征条件和对应的类别标签。当新样本进入决策树时,它会根据特征的条件依次遵循路径,最终确定样本所属的类别。
- 条件概率分布:决策树也可以看作是定义在特征空间与类别空间上的条件概率分布。每个内部节点表示一个特征条件,每个叶子节点表示一个类别,并且沿着路径的条件概率决定了样本被分类到不同的类别。
- 学习过程:决策树的学习过程通常包括以下步骤:
- 特征选择:选择最佳的特征作为根节点,以最大化分类效果。
- 分裂节点:将数据集根据选定的特征进行分割,生成子节点。
- 递归学习:对每个子节点递归应用上述步骤,直到达到停止条件(例如,达到最大深度、样本数量小于阈值等)。
- 剪枝(可选):在生成决策树后,可以应用剪枝算法来减小过拟合风险。
- 优点:决策树具有易于理解和解释的特点,可以生成清晰的分类规则。它们适用于离散和连续特征,对缺失值具有一定的容忍性,且在某些情况下表现良好。
- 缺点:决策树容易过拟合训练数据,因此需要进行剪枝等正则化方法。它们可能在处理复杂问题时产生过多的规则,导致模型过于复杂。此外,决策树对数据中的噪声和不稳定性敏感。
决策树是一种强大的机器学习工具,适用于各种分类和回归任务。通过合适的参数调整和正则化方法,可以改善其性能并减小过拟合的风险。在实际应用中,决策树通常与集成学习方法(如随机森林和梯度提升树)相结合,以进一步提高模型的性能。
它可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
特征空间(Feature Space)和类空间(Class Space)是机器学习中常用的两个概念,它们用于描述模型和数据的属性。
- 特征空间(Feature Space):
- 特征空间是指用来描述样本(数据点)的属性或特征的空间。每个样本可以在特征空间中表示为一个向量,其中每个维度对应一个特征。
- 在特征空间中,每个维度表示一个特征,而每个样本由这些特征的值组成。例如,在文本分类任务中,特征空间可能包括词汇表中的单词,每个维度表示一个单词在文本中的出现次数或TF-IDF值。
- 特征空间的维度取决于数据集中的特征数量,可以是高维的(包含许多特征)或低维的(包含较少的特征)。
- 类空间(Class Space):
- 类空间是指用来描述样本所属类别或标签的空间。每个样本都被分配到类空间中的一个类别。
- 在分类问题中,类空间包括所有可能的类别或标签。每个样本在类空间中被分配到一个类别,以表示其所属类别。
- 类空间通常是离散的,每个类别由一个唯一的标识符表示。例如,二元分类问题中的类空间可能包括 “正类” 和 “负类” 两个类别。
在机器学习任务中,特征空间和类空间之间的映射关系是模型的关键。机器学习模型的目标是学习如何从特征空间中的数据映射到类空间中的类别。决策树、支持向量机、神经网络等各种模型都是用来建立特征空间到类空间的映射关系,并用于分类或回归任务。
总之,特征空间描述了数据的特征属性,而类空间描述了数据的类别或标签,它们在机器学习中是重要的概念,用于建模和解决各种问题。
其主要优点:1.模型具有可读性;2.分类速度快
| 阶段 | 操作 |
|---|---|
| 学习时 | 利用训练数据,根据损失函数最小化的原则建立决策树模型 |
| 预测时 | 对新的数据,利用决策树模型进行分类 |
决策树学习通常包括3个步骤:特征选择->决策树的生成->决策树的修剪
5.1决策树模型与学习
5.1.1决策树模型
定义5.1(决策树):分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型:内部结点(internalnode)和叶结点(leaf node)。内部结点表示一个特征或属性,叶结点表示一个类。
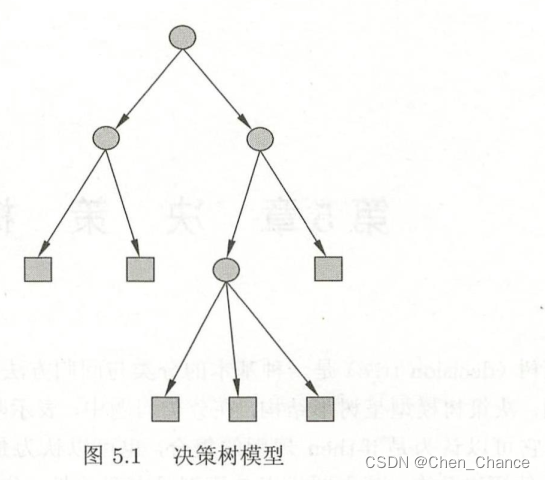
5.1.2决策树与if-then规则
5.1.3决策树与条件概率分布
5.1.4决策树学习
决策树学习用损失函数表示这一目标。如下所述,决策树学习的损失函数通常是正则化的极大似然函数。决策树学习的策略是以损失函数为目标函数的最小化。
当损失函数确定后,学习问题就变为在损失函数意义下选择最优决策树的问题。因为从所有可能的决策树中选取最优决策树是NP完全问题,所以现实中决策树学习算法通常采用启发式方法,近似求解这一最优化问题,这样得到的决策树是次最优(sub-optimal)的。
- 从所有可能的决策树中选择最优决策树是一个非常复杂的问题,它属于NP完全问题,这意味着在现实世界中,找到确切的最优解可能需要大量时间,甚至是不可行的。
- 为了解决这个问题,决策树学习算法通常采用一种称为启发式方法的策略。这就像在迷宫中找到出口,你可能不会尝试每个可能的路径,而是根据一些规则或经验选择下一步,希望最终找到出口。在决策树学习中,这些规则和经验可以是分裂节点的标准、剪枝策略、节点的排序等。
- 使用这些启发式方法,我们可以获得一个次最优(sub-optimal)的决策树,这意味着它可能不是全局最优解,但在实践中性能仍然很好。次最优的决策树通常能够很好地拟合训练数据,并且具有较好的泛化性能,可以用于对未见数据的分类或回归。
简而言之,决策树学习算法面临一个非常复杂的优化问题,通常无法找到全局最优解。因此,它使用一些经验法则和启发式方法来近似求解这个问题,最终得到一个次最优的决策树,以在实际应用中表现良好。这类似于在实际问题中使用经验和直觉来做出决策,而不是尝试每种可能的选择。
决策树学习算法包含特征选择、决策树的生成与决策树的剪枝过程。由于决策树表示一个条件概率分布,所以深浅不同的决策树对应着不同复杂度的概率模型。决策树的生成对应于模型的局部选择,决策树的剪枝对应于模型的全局选择。决策树的生成只考虑局部最优,相对地,决策树的剪枝则考虑全局最优。
决策学习常用的算法有ID3、C4.5与CART,下面结合这些算法分别叙述决策树学习的特征选择、决策树的生成和剪枝过程。
5.2特征选择
5.2.1特征选择问题
通常特征选择的准则是信息增益或信息增益比
5.2.2信息增益
为了便于说明,先给出熵与条件熵的定义
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量,其概率分布为
P ( X = x i ) = p i , i = 1 , 2 , . . . , n P(X=x_i)=p_i,i=1,2,...,n P(X=xi)=pi,i=1,2,...,n
则随机变量X的熵定义为(若 p i = 0 p_i=0 pi=0,则定义 0 l o g 0 = 0 0log0=0 0log0=0)
H ( X ) = − ∑ i = 1 n p i l o g p i H(X)=-\sum\limits_{i=1}^n p_i log p_i H(X)=−i=1∑npilogpi
由于熵只依赖于X的分布,而与X的取值无关,所以也可将X的熵记作H§,即
H ( p ) = − ∑ i = 1 n p i l o g p i H(p)=-\sum\limits_{i=1}^n p_i log p_i H(p)=−i=1∑npilogpi
熵越大,随机变量的不确定性就越大。从定义可验证
0 ≤ H ( p ) ≤ l o g n 0≤H(p)≤log n 0≤H(p)≤logn
它是信息熵的基本性质之一。这是信息熵 H ( p ) H(p) H(p) 的性质,不需要再次证明。
设有随机变量 ( X , Y ) (X,Y) (X,Y),其联合概率分布为
P ( X = x i , Y = y j ) = p i j , i = 1 , 2 , . . . , n ; j = 1 , 2 , . . . , m P(X=x_i,Y=y_j)=p_{ij},i=1,2,...,n;j=1,2,...,m P(X=xi,Y=yj)=pij,i=1,2,...,n;j=1,2,...,m
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵(conditional entropy)H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=\sum\limits_{i=1}^n p_iH(Y|X=x_i) H(Y∣X)=i=1∑npiH(Y∣X=xi)
这里, p i = P ( X = x i ) , i = 1 , 2 , . . . , n p_i=P(X=x_i),i=1,2,...,n pi=P(X=xi),i=1,2,...,n
让我们通过一个简单的例子来计算条件熵。
假设我们有两个随机变量X和Y,它们的联合分布如下:
X/Y Y=1 Y=2 X=1 0.2 0.1 X=2 0.3 0.4 X=3 0.1 0.2 首先,我们需要计算条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X),然后根据这个分布计算条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)。让我们按照步骤进行计算:
步骤 1:计算边际概率分布 P ( X ) P(X) P(X)
首先,我们计算随机变量X的边际概率分布 P ( X ) P(X) P(X),即X取每个可能值的概率。
P ( X = 1 ) = 0.2 + 0.1 + 0.1 = 0.4 P(X=1) = 0.2 + 0.1 + 0.1 = 0.4 P(X=1)=0.2+0.1+0.1=0.4
P ( X = 2 ) = 0.3 + 0.4 + 0.2 = 0.9 P(X=2) = 0.3 + 0.4 + 0.2 = 0.9 P(X=2)=0.3+0.4+0.2=0.9
P ( X = 3 ) = 0.1 + 0.2 = 0.3 P(X=3) = 0.1 + 0.2 = 0.3 P(X=3)=0.1+0.2=0.3
步骤 2:计算条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)
接下来,我们计算条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X),即在给定X的条件下Y的概率分布。我们可以使用条件概率的定义来计算它:
P ( Y = 1 ∣ X = 1 ) = P ( X = 1 , Y = 1 ) P ( X = 1 ) = 0.2 0.4 = 0.5 P(Y=1|X=1) = \frac{P(X=1, Y=1)}{P(X=1)} = \frac{0.2}{0.4} = 0.5 P(Y=1∣X=1)=P(X=1)P(X=1,Y=1)=0.40.2=0.5
P ( Y = 2 ∣ X = 1 ) = P ( X = 1 , Y = 2 ) P ( X = 1 ) = 0.1 0.4 = 0.25 P(Y=2|X=1) = \frac{P(X=1, Y=2)}{P(X=1)} = \frac{0.1}{0.4} = 0.25 P(Y=2∣X=1)=P(X=1)P(X=1,Y=2)=0.40.1=0.25
P ( Y = 1 ∣ X = 2 ) = P ( X = 2 , Y = 1 ) P ( X = 2 ) = 0.3 0.9 = 1 3 P(Y=1|X=2) = \frac{P(X=2, Y=1)}{P(X=2)} = \frac{0.3}{0.9} = \frac{1}{3} P(Y=1∣X=2)=P(X=2)P(X=2,Y=1)=0.90.3=31
P ( Y = 2 ∣ X = 2 ) = P ( X = 2 , Y = 2 ) P ( X = 2 ) = 0.4 0.9 ≈ 0.4444 P(Y=2|X=2) = \frac{P(X=2, Y=2)}{P(X=2)} = \frac{0.4}{0.9} \approx 0.4444 P(Y=2∣X=2)=P(X=2)P(X=2,Y=2)=0.90.4≈0.4444
P ( Y = 1 ∣ X = 3 ) = P ( X = 3 , Y = 1 ) P ( X = 3 ) = 0.1 0.3 ≈ 0.3333 P(Y=1|X=3) = \frac{P(X=3, Y=1)}{P(X=3)} = \frac{0.1}{0.3} \approx 0.3333 P(Y=1∣X=3)=P(X=3)P(X=3,Y=1)=0.30.1≈0.3333
P ( Y = 2 ∣ X = 3 ) = P ( X = 3 , Y = 2 ) P ( X = 3 ) = 0.2 0.3 ≈ 0.6667 P(Y=2|X=3) = \frac{P(X=3, Y=2)}{P(X=3)} = \frac{0.2}{0.3} \approx 0.6667 P(Y=2∣X=3)=P(X=3)P(X=3,Y=2)=0.30.2≈0.6667
步骤 3:计算条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X)
现在我们可以使用条件熵的定义来计算 H ( Y ∣ X ) H(Y|X) H(Y∣X),根据公式:
H ( Y ∣ X ) = ∑ i = 1 n P ( X = x i ) H ( Y ∣ X = x i ) H(Y|X) = \sum_{i=1}^n P(X=x_i) H(Y|X=x_i) H(Y∣X)=i=1∑nP(X=xi)H(Y∣X=xi)
代入我们计算得到的条件概率值:
H ( Y ∣ X ) = P ( X = 1 ) ⋅ [ − ( 0.5 log 2 ( 0.5 ) + 0.25 log 2 ( 0.25 ) ) ] + P ( X = 2 ) ⋅ [ − ( 1 3 log 2 ( 1 3 ) + 0.4444 log 2 ( 0.4444 ) ) ] + P ( X = 3 ) ⋅ [ − ( 0.3333 log 2 ( 0.3333 ) + 0.6667 log 2 ( 0.6667 ) ) ] H(Y|X) = P(X=1) \cdot [-(0.5 \log_2(0.5) + 0.25 \log_2(0.25))] + P(X=2) \cdot [-(\frac{1}{3} \log_2(\frac{1}{3}) + 0.4444 \log_2(0.4444))] + P(X=3) \cdot [-(0.3333 \log_2(0.3333) + 0.6667 \log_2(0.6667))] H(Y∣X)=P(X=1)⋅[−(0.5log2(0.5)+0.25log2(0.25))]+P(X=2)⋅[−(31log2(31)+0.4444log2(0.4444))]+P(X=3)⋅[−(0.3333log2(0.3333)+0.6667log2(0.6667))]
计算每个部分的值并求和:
H ( Y ∣ X ) ≈ 0.8464 + 0.6492 + 0.6365 ≈ 2.1321 H(Y|X) \approx 0.8464 + 0.6492 + 0.6365 \approx 2.1321 H(Y∣X)≈0.8464+0.6492+0.6365≈2.1321
所以,在给定随机变量X的条件下,随机变量Y的条件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X) 约为2.1321。
当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时,所对应的熵与条件熵分别称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy)。此时,若有0概率,令0log0=0
经验熵和经验条件熵是信息论中的概念,它们涉及到基于实际观测数据来估计随机变量的熵和条件熵。
- 经验熵(Empirical Entropy):
经验熵是指根据实际观测数据来估计一个随机变量的熵。通常情况下,我们没有完全的先验知识,无法直接知道随机变量的概率分布。因此,我们可以使用观测到的数据来估计这个分布,最常见的估计方法之一是极大似然估计。通过统计数据中每个事件(或取值)的频率,我们可以估计随机变量的概率分布,然后计算熵。这个估计得到的熵被称为经验熵。- 经验条件熵(Empirical Conditional Entropy):
经验条件熵是在已知另一个随机变量的条件下,根据实际观测数据估计另一个随机变量的条件熵。与经验熵类似,我们可以使用观测到的数据来估计条件概率分布,然后计算条件熵。这个估计得到的条件熵被称为经验条件熵。这两个概念的核心思想是,当我们不知道真实的概率分布,但有一些观测数据时,我们可以基于数据来估计信息熵和条件熵,以便在实际问题中应用信息论的概念。这对于机器学习、数据分析和模型建立等领域非常有用,因为通常我们只能获得有限的数据,而无法获得完整的概率分布信息。所以,经验熵和经验条件熵允许我们在缺乏完整信息的情况下进行信息论分析。
信息增益(information gain)表示得知特征X的信息而使得类Y的信息不确定性减少的程度
定义5.2(信息增益)特征A对训练数据集D的信息增益 g ( D , A ) g(D,A) g(D,A),定义为集合D的经验熵 H ( D ) H(D) H(D)与特征A给定条件下D的经验条件熵 H ( D ∣ A ) H(D|A) H(D∣A)之差,即
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
一般地,熵H(Y)与条件熵H(Y|X)之差称为互信息(mutual information)。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
根据信息增益准则的特征选择方法是:对训练数据集(或子集)D,计算其每个特征的信息增益,并比较它们的大小,选择信息增益最大的特征。
5.2.3信息增益比
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题。
以信息增益作为划分训练数据集的特征存在偏向于选择取值较多的特征的问题,这是因为信息增益的计算方式使得在有更多取值的特征上产生更多的子分支,从而可能导致信息增益偏向于选择取值较多的特征。让我更详细地解释这个问题。
信息增益的计算方式涉及到条件熵(Conditional Entropy),其计算公式为:
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ⋅ H ( D i ) H(D|A) = \sum_{i=1}^n \frac{|D_i|}{|D|} \cdot H(D_i) H(D∣A)=i=1∑n∣D∣∣Di∣⋅H(Di)
其中, H ( D ∣ A ) H(D|A) H(D∣A) 是在特征 A A A 条件下数据集 D D D 的条件熵, D i D_i Di 是特征 A A A 的每个取值对应的子数据集, ∣ D i ∣ |D_i| ∣Di∣ 表示子数据集的大小, ∣ D ∣ |D| ∣D∣ 表示总数据集的大小。
注意到在计算条件熵时,分母 ∣ D ∣ |D| ∣D∣ 是不变的,但分子 ∣ D i ∣ |D_i| ∣Di∣ 取决于特征 A A A 的取值个数。如果特征 A A A 的取值较多,那么就会有更多的 ∣ D i ∣ |D_i| ∣Di∣ 需要相加,这会导致条件熵的计算中有更多的项。
这个问题的关键在于,条件熵的值越低,信息增益越高。因此,如果特征 A A A 具有更多的取值,它可能会导致更多的子分支,每个子分支对应一个取值,而每个子分支的条件熵通常较低,因为数据更容易在这个子分支中进行分类。这会使得信息增益在计算时受到特征取值数量的影响,偏向于选择取值较多的特征。
为了克服这个问题,可以考虑使用一些改进的特征选择准则,例如信息增益比(Information Gain Ratio)或基尼不纯度(Gini impurity)。这些准则在计算中会考虑到特征取值的数量,以减轻信息增益对取值较多特征的偏向,使得特征选择更加平衡。
5.3决策树的生成
5.3.1 ID3算法
5.3.2 C4.5的生成算法
5.4决策树的剪枝
5.5 CART算法
5.5.1 CART生成
5.5.2 CART剪枝
相关文章:

李航老师《统计学习方法》第五章阅读笔记
决策树(decision tree)是一种基本的分类与回归方法。本章主要讨论用于分类的决策树。决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。 以下是关于分类决策树的一些基本概念和特点: 树形结构&am…...

iOS16新特性:实时活动-在锁屏界面实时更新APP消息 | 京东云技术团队
简介 之前在 《iOS16新特性:灵动岛适配开发与到家业务场景结合的探索实践》 里介绍了iOS16新的特性:实时更新(Live Activity)中灵动岛的适配流程,但其实除了灵动岛的展示样式,Live Activity还有一种非常实用的应用场景…...
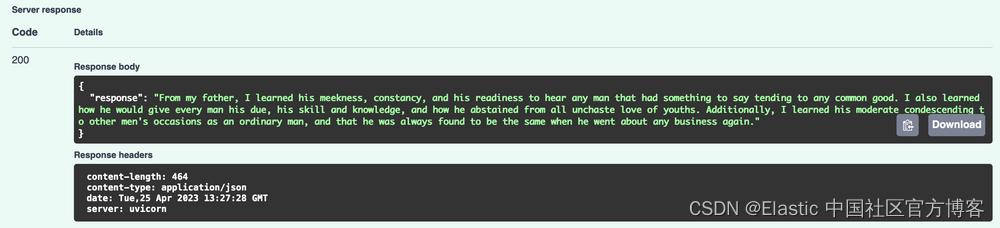
使用 Elasticsearch、OpenAI 和 LangChain 进行语义搜索
在本教程中,我将引导您使用 Elasticsearch、OpenAI、LangChain 和 FastAPI 构建语义搜索服务。 LangChain 是这个领域的新酷孩子。 它是一个旨在帮助你与大型语言模型 (LLM) 交互的库。 LangChain 简化了与 LLMs 相关的许多日常任务,例如从文档中提取文本…...
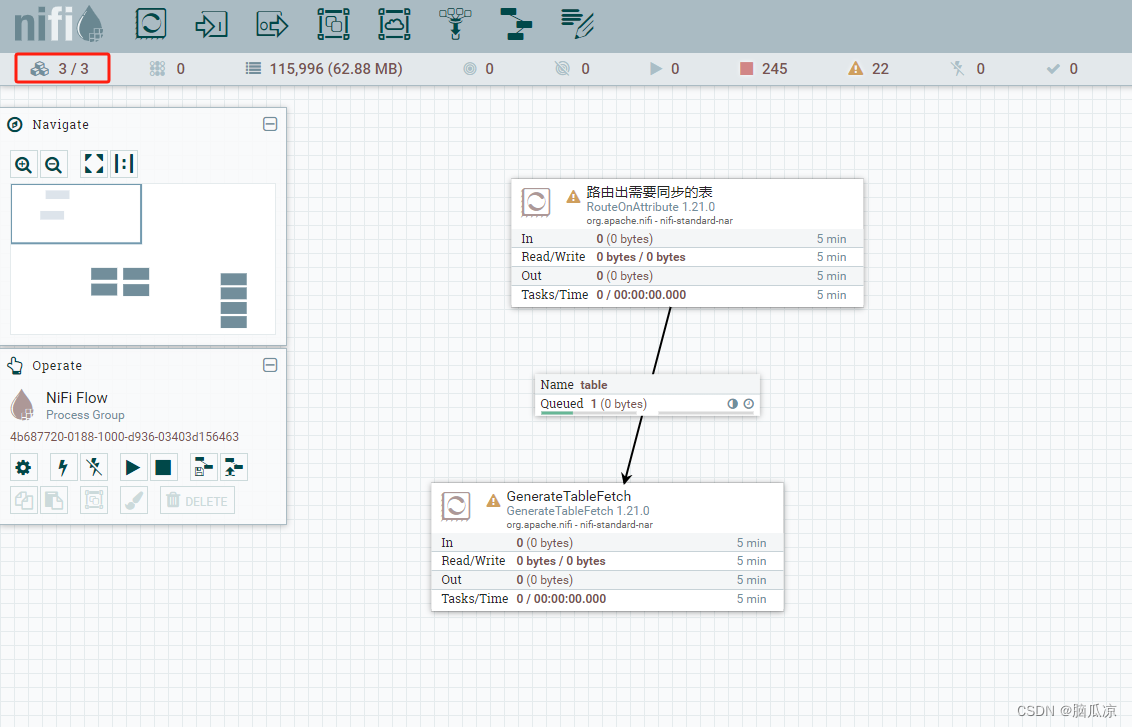
NIFI集群_队列Queue中数据无法清空_清除队列数据报错_无法删除queue_解决_集群中机器交替重启删除---大数据之Nifi工作笔记0061
今天发现,有两个处理器,启动以后,数据流不过去,后来,锁定问题在,queue队列上面,因为别的队列都可以通过,右键,empty queue清空,就是 这个队列不行,这个队列无法被删除,至于为什么导致这样的, 猜测是因为之前,流程设计好以后,队列没有设置背压,也没有设置队列中的内容大小和fl…...

leetcode20. 有效的括号 [简单题]
题目 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。每个右括号都有一个对应的相同类型…...

ubuntu20.04下源码编译colmap
由于稠密重建需要CUDA,因此先安装CUDA,我使用的是3050GPU,nvidia-smi显示最高支持CUDA11.4。 不要用sudo apt安装,版本较低,30系显卡建议安装CUDA11.0以上,这里安装了11.1版本。 下载: cuda_1…...
Jumpserver堡垒机
一、堡垒机概述 1、堡垒机的基本概念 堡垒机也是一台服务器,在一个特定的网络环境下,为了保障网络和数据不受来自外部和内部用户的入侵和破坏,而运用各种技术手段实时收集、监控网络环境中每一个组成部分(服务器)的系…...

第一百五十三回 如何实现滑动窗口
文章目录 概念介绍实现方法示例代码 我们在上一章回中介绍了自定义组件实现游戏摇杆相关的内容,本章回中将介绍 如何实现滑动窗口.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在本章回中介绍的滑动窗口表示在屏幕底部向上滑动时弹出一个窗口&a…...

Oracle 12c自动化管理特性的新进展:自动备份、自动恢复和自动维护功能的优势|oracle 12c相对oralce 11g的新特性(3)
一、前言: 前面几期讲解了oracle 12c多租户的使用、In-Memory列存储来提高查询性能以及数据库的克隆、全局数据字典和共享数据库资源的使用 今天我们讲讲oracle 12c的另外的一个自动化管理功能新特性:自动备份、自动恢复、自动维护的功能 二、自动备份、自动恢复、自动维护…...

Redis——Jedis中hash类型使用
hset 和 hget hset可以逐一添加key和value,也可以通过map类型来直接添加多组fields 而hget则返回string类型,如果元素不存在则返回null private static void hsetAndHget(Jedis jedis) {jedis.flushAll();jedis.hset("key", "f1"…...
肖sir__项目实战讲解__004
项目实战讲解 一、项目的类型 金融类: 保险(健康险理财险)、证券、基金(股票型基金、混合型基金、指数型基金、债券型基金、 天天基金网(ETF基金、货币型基金、量化基金)、银行、贷款、信用卡、外汇、二元期权、期货原油、blockchain、 数字货币、黄金白…...

数据库数据恢复-ORACLE常见故障有哪些?恢复数据的可能性高吗?
ORACLE数据库常见故障: 1、ORACLE数据库无法启动或无法正常工作。 2、ORACLE数据库ASM存储破坏。 3、ORACLE数据库数据文件丢失。 4、ORACLE数据库数据文件部分损坏。 5、ORACLE数据库DUMP文件损坏。 ORACLE数据库数据恢复可能性分析: 1、ORACLE数据库无…...

合规性管理如何帮助产品团队按时交付?
成功的产品和产品发布背后通常需要经过一个涉及多个监督机构、多功能团队和利益相关者的复杂流程。在组织的治理、风险管理和合规性(GRC)框架下,产品团队不仅需要追求市场创新,还需要确保符合所有适用的法规、标准和合同要求。由于…...
从平均数到排名算法
平均数用更少的数字,概括一组数字。属于概述统计量、集中趋势测度、位置测度。中位数是第二常见的概述统计量。许多情况下比均值更合适。算术平均数是3中毕达哥拉斯平均数之一,另外两种毕达哥拉斯平均数是几何平均数和调和平均数。 算术平均 A M 1 n ∑…...

如何使用ESP8266微控制器和Nextion显示器为Home Assistant展示温度传感器和互联网天气预报
第一部分:引言与项目概述 在智能家居领域,实时监控和显示环境数据已经成为了一个热门的话题。无论是室内温度、室外温度,还是游泳池的温度,都可以通过各种传感器轻松获取。但如何将这些数据以直观、美观的方式展现出来呢…...
阻塞队列-生产者消费者模型
阻塞队列介绍标准库阻塞队列使用基于阻塞队列的简单生产者消费者模型。实现一个简单型阻塞队列 (基于数组实现) 阻塞队列介绍 不要和之前学多线程的就绪队列搞混; 阻塞队列:也是一个队列,先进先出。带有特殊的功能 &…...

Vector Art - 矢量艺术
什么是矢量艺术? 矢量图形允许创意人员构建高质量的艺术作品,具有干净的线条和形状,可以缩放到任何大小。探索这种文件格式如何为各种规模的项目提供创造性的机会。 什么是矢量艺术作品? 矢量艺术是由矢量图形组成的艺术。这些图形是基于…...
)
ruoyi-nbcio增加flowable流程待办消息的提醒,并提供右上角的红字数字提醒(一)
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 1、数据库表方面 在原来sys_notice修改基础上增加一个表叫sys_notice_send 表结构如下: DROP …...
数据结构:二叉树的基本概念
文章目录 1. 二叉树的定义2. 二叉树的特点3. 特殊二叉树斜树满二叉树完全二叉树 4. 二叉树的性质 1. 二叉树的定义 如果我们猜一个100以内的数字,该怎么猜才能理论最快呢? 第一种方式:从1,2一直猜到100, 反正数字都是100以内,总能猜到的 第二种方式:先猜50,如果比结果小,猜75…...

利用Socks5代理IP加强跨界电商爬虫的网络安全
随着跨界电商的兴起,爬虫技术在这个领域变得越来越重要。然而,网络安全一直是一个值得关注的问题。在本文中,我们将讨论如何利用代理IP和Socks5代理来增强跨界电商爬虫的网络安全,确保稳定和可靠的数据采集,同时避免封…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
