数据结构与算法之时间复杂度和空间复杂度(C语言版)
1. 时间复杂度
1.1 概念
简而言之,算法中的基本操作的执行次数,叫做算法的时间复杂度。也就是说,我这个程序执行了多少次,时间复杂度就是多少。
比如下面这段代码的执行次数:
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}Func1执行的基本操作次数:
F(N) = N^2 + 2*N + 10
在这里两层for循环的次数是N^2,第二个for循环的次数是2*N,while循环的次数是10
所以这个算法中的基本操作次数就是 N^2 + 2*N + 10。
那我们的时间复杂度就是这个吗,其实不是的。实际上我们在计算时间复杂度的时候,我们并不一定要计算精确的执行次数,而只需要大概执行次数。
这又是为什么呢?
当N = 10的时候,F(N) = 130
当 N = 100 的时候,F(N) = 10210
当 N = 1000 的时候,F(N) = 1002010
我们发现当N趋于无穷大的时候,对F(N)影响最大的是N^2,这就跟我们在数学里找极限一样,抓大头,找影响最大的一项,用影响最大的一项来表示我们的时间复杂度
这种表示方法我们称作大O的渐进表示法。
1.2大O的渐进表示法
大O符号(Big O notation):用于描述函数渐进行为的数学符号。
基本执行次数用大O阶方法表示的规则:
1. 如果执行次数中出现加法常数(无论多大,只要是常数),用1来代替。
2. 如果执行次数是多项式,执行次数只保留最高阶项(最高次项)
3. 如果最高阶项存在且不是1,舍去系数。
4.经过1,2,3操作得到的结果就是大O阶表示。
所以我们上面的F(N) = N^2 + 2*N + 10 用大O阶表示就是 O(N^2)。
1.3 最好,平均,最坏情况
有些算法的时间复杂度是存在最好,平均,最坏情况的。
1.最好情况:基本操作次数的最小值
2.平均情况:期望的基本操作次数
3.最坏情况:基本操作次数的最大值
但是在实际中我们都是用最坏情况来表示时间复杂度
1.4 时间复杂度例题
1.4.1 例题1
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}答案:O(N)
基本执行次数是(2 * N + 10),用大O阶表示为O(N)
1.4.2 例题2
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}答案:O(M+N)
基本执行次数是M+N次,由于有两个未知数M和N,所以大O阶表示为O(M+N)
1.4.3 例题3
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}答案:O(1)
基本执行次数是100次,用大O阶表示为O(1)
1.4.4 例题4
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}答案:O(N^2)
基本操作次数是(n-1)+(n-2)+(n-3)+....+3+2+1 = ((n + 1) * n) / 2
最好情况就是遍历一次就排序成功,基本操作次数是n-1,大O阶表示是O(N)
最坏情况就是全部遍历完,基本操作次数是((n + 1) * n) / 2,大O阶表示为O(N^2)
时间复杂度一般看最坏情况,为O(N^2)
大O表示为O(N^2)
1.4.5 例题5
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}答案:O(log N)
这个算法是二分查找
最好情况是查找一次,为O(1)
最坏情况是begin = end 了,只剩了一个元素,我们可以设循环的次数是x,一次循环我们是砍掉了一半的数组元素,那到最后没有元素了,说明n / 2^x = 1
所以x = log n(以2为底)。时间复杂度的大O阶表示就是O(logN)。
我们规定以2为底的对数函数写成 log N
1.4.6 例题6
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}答案:O(N)
基本操作次数:这个函数一共递归了N次,时间复杂度就是O(N)
1.4.7 例题7
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}答案:O(2^N)
基本操作次数:这个函数递归了1+2+4+8+... 是一个不完整的等比数列,在N<3之后不会递归,但是不影响整体的趋势,可以忽略不计,这个等比数列的和是2^n - 1
所以大O阶表示为O(2^n)
2.空间复杂度
2.1概念
空间复杂度指的是临时占用存储空间大小的量度,需要注意的是空间复杂度并不是程序占了多少个字节的空间,因为没有什么太大意义,所以空间复杂度指的是新创建的变量个数
空间复杂度计算规则和时间复杂度基本一致,用大O阶渐渐表示法。
注意⚠️⚠️⚠️:
1. 计算空间复杂度时,一般不需要考虑函数的形式参数。空间复杂度主要关注的是算法执行过程中所占用的额外空间,而函数的形式参数在函数调用时会被压入调用栈中,属于函数调用过程中的内存分配,并不计入空间复杂度的计算。
2. 递归算法在每次递归调用时需要维护函数调用栈,而函数调用栈会占用额外的内存空间,所以其空间复杂度为递归所使用的堆栈空间的大小。
2.2 空间复杂度例题
2.2.1 例题1
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i) {if (a[i - 1] > a[i]) {Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}这个冒泡排序临时创建的变量分别是 end , exchange 和 i 一共三个,是常数个。
所以空间复杂度用大O阶表示为O(1)
2.2.2 例题2
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}这个算法我们直接看新创建的变量是fibArray这个数组,是动态开辟的一个数组,开辟了n+1个空间,还有个i变量,一共是n+2个变量。
用大O阶表示为O(n)
2.2.3 例题3
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}首先我们要明确的是这是一个函数递归调用
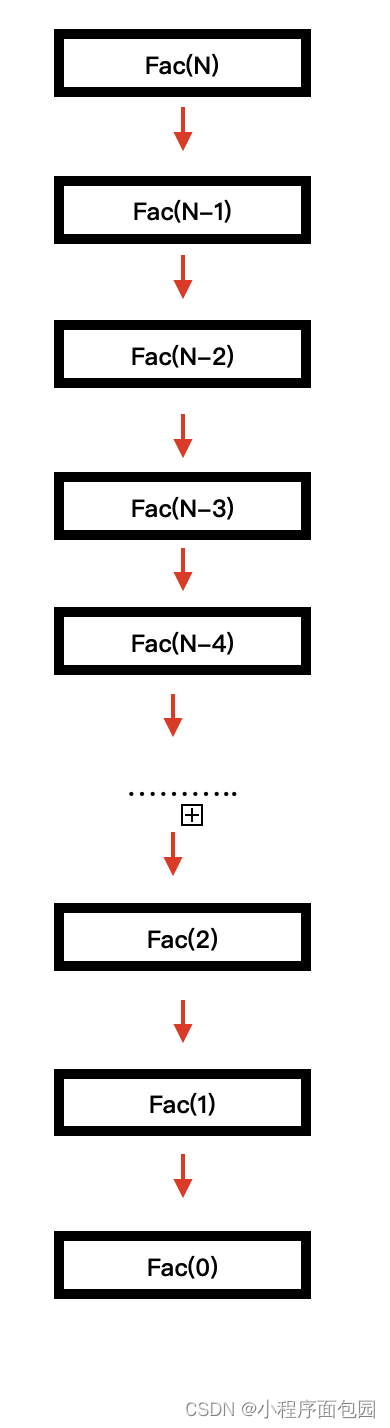
我们函数递归一共要递归N次,共创建新的栈空间N个
所以空间复杂度为O(N)
2.2.4 例题4
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}此时的空间复杂度是多少呢? O(2^N)? 还是O(N)?
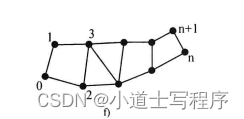
我们画图来说明
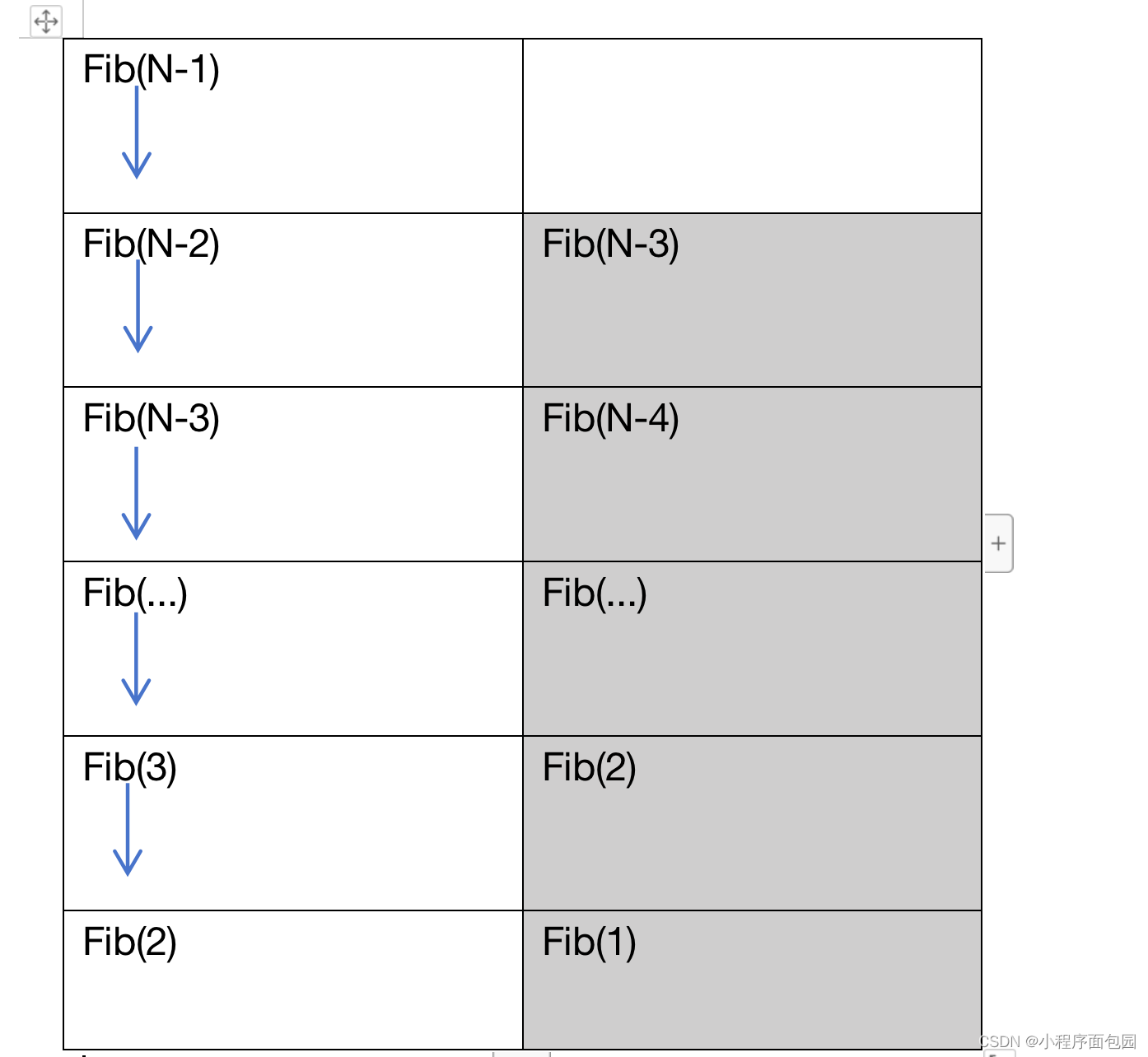
我们来看这个函数的递归调用并不是同时进行的,而是先调用左边的,左边调用完了,最下面Fib(2)往回销毁空间之后才去调用Fib(1),也就是在这个时候才开辟Fib(1)的空间
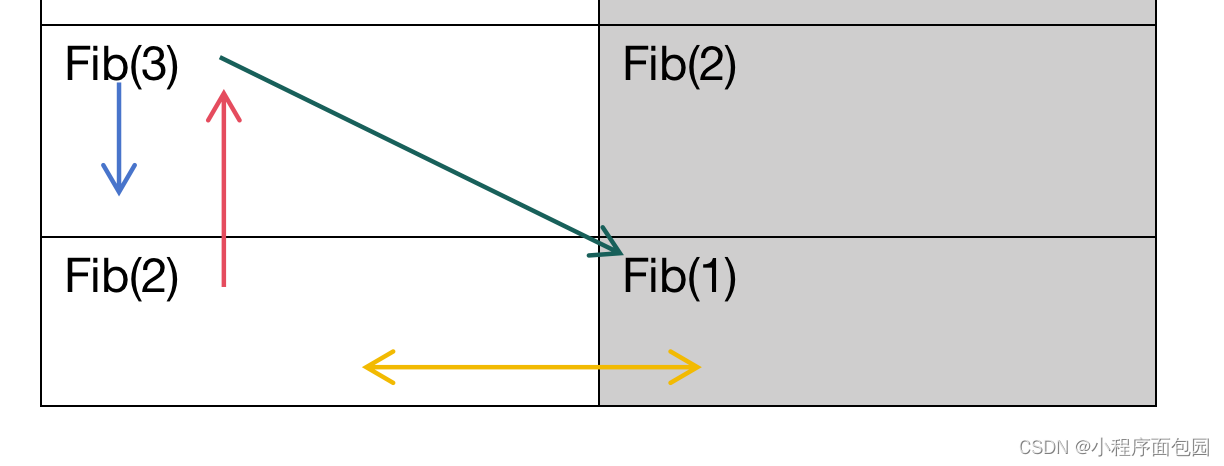
蓝色箭头代表从Fib(3)到Fib(2)先开辟Fib(2)的栈空间,当调用结束的时候,这段空间就要销毁,于是就有了红色的箭头代表销毁Fib(2)的空间,销毁之后我们才开始调用Fib(1),绿色箭头代表调用Fib(1),此时就要开辟Fib(1)的空间,要知道的是我们刚刚销毁一个栈空间,现在又要开辟一个栈空间,所以空间是被重复利用的,也就是黄色的箭头,Fib(1)的空间跟Fib(2)的空间是同一块空间。
所以我们真正开辟的空间只有从Fib(N)到Fib(2)这一段,其他的调用函数,都是在重复利用栈空间的过程。
所以空间复杂度是O(N)
总结:时间是累积的,一去不复返
空间是可以重复利用的。
3.常见复杂度的对比
| 常数阶 | O(1) | 5201314 |
| 线性阶 | O(N) | 3N+1 |
| 平方阶 | O(N^2) | 2N^2 + 3N + 1 |
| 对数阶 | O(logN) | 3log(2)N + 2 |
| NlogN阶 | O(NlogN) | 2N+3Nlog(2)N + 1 |
| 立方阶 | O(N^3) | 3N^3+2N^2+N+1 |
| 指数阶 | O(2^N) | 2^N |
O(1) < O(log n) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
相关文章:

数据结构与算法之时间复杂度和空间复杂度(C语言版)
1. 时间复杂度 1.1 概念 简而言之,算法中的基本操作的执行次数,叫做算法的时间复杂度。也就是说,我这个程序执行了多少次,时间复杂度就是多少。 比如下面这段代码的执行次数: void Func1(int N) {int count 0;for…...

TLS/SSL(十) session缓存、ticket 票据、TLS 1.3的0-RTT
一 TLS优化手段 TLS 为了提升握手速度而提出优化手段,主要是减少TLS握手中RTT消耗的时间关于session cache和session ticket,nginx关于ssl握手的地方都有影子 [指令] https面经 ① session 缓存 resume: 重用,复用 案例: 第二次访问www.baidu.com 说明&#x…...
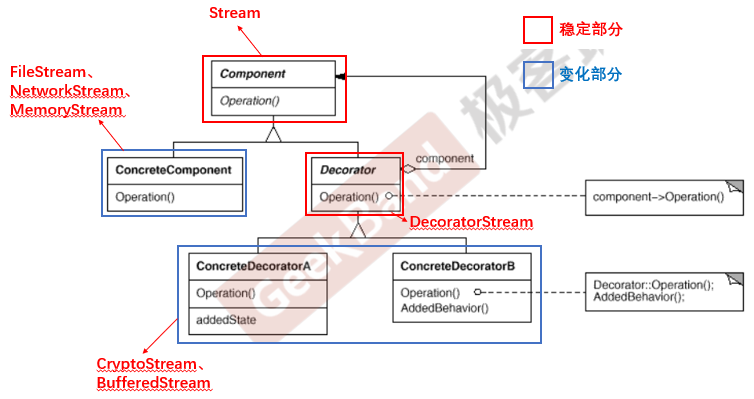
C++设计模式_06_Decorator 装饰模式
本篇将会介绍Decorator 装饰模式,它是属于一个新的类别,按照C设计模式_03_模板方法Template Method中介绍的划分为“单一职责”模式。 “单一职责”模式讲的是在软件组件的设计中,如果责任划分的不清晰,使用继承得到的结果往往是随…...
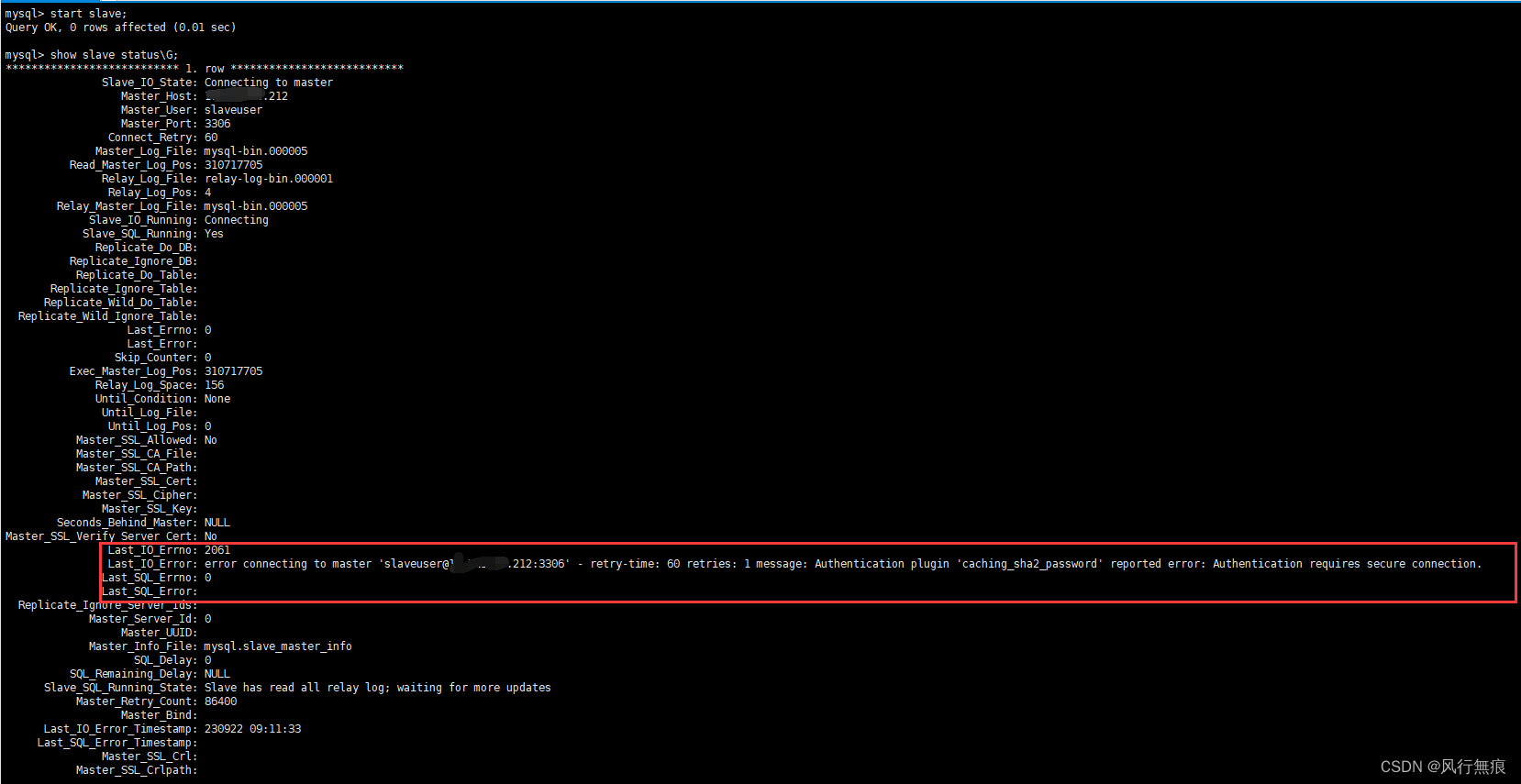
MySQL 8.0数据库主从搭建和问题处理
错误处理: 在从库通过start slave启动主从复制时出现报错 Last_IO_Error: error connecting to master slaveuser10.115.30.212:3306 - retry-time: 60 retries: 1 message: Authentication plugin caching_sha2_password reported error: Authentication require…...
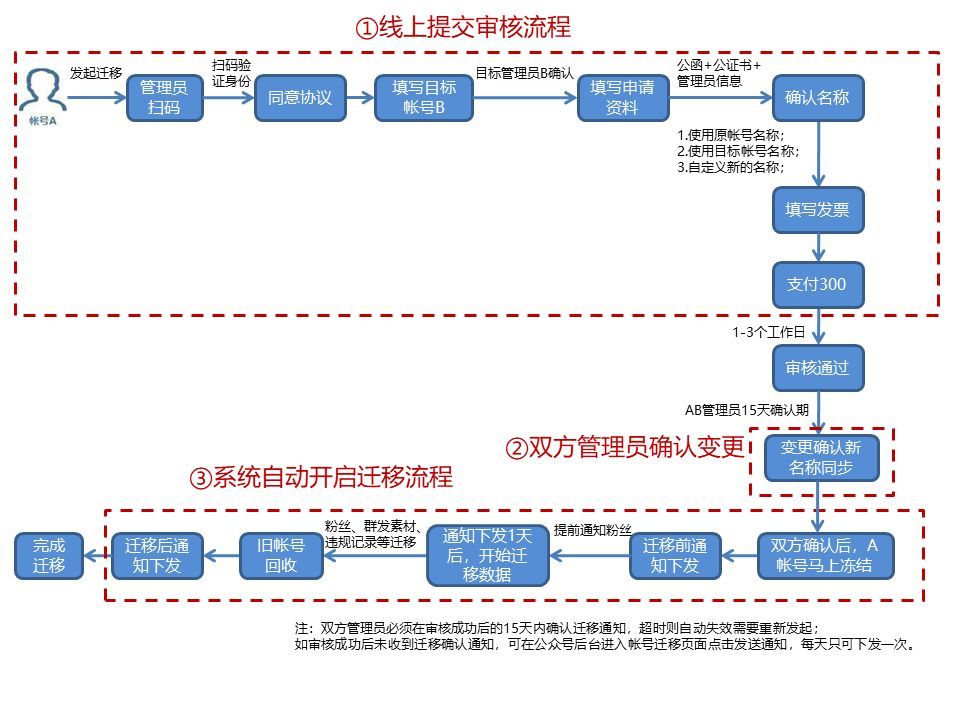
公众号迁移多久可以完成?
公众号账号迁移的作用是什么?只能变更主体吗?长期以来,由于部分公众号在注册时,主体不准确的历史原因,或者公众号主体发生合并、分立或业务调整等现实状况,在公众号登记主体不能对应实际运营人的情况下&…...
使用)
Spring Cloud Stream Kafka(3.2.2版本)使用
问题 正在尝试只用Spring Cloud Stream Kafka。 步骤 配置 spring:cloud:function:definition: project2Building stream:kafka:binder:brokers: xxxx:9002configuration:enable.auto.commit: falsesession.timeout.ms: 30000max.poll.records: 30allow.auto.create.top…...

8位微控制器上的轻量级SM2加密算法实现:C语言详细指南与完整代码解析
引言 在当今的数字化世界中,安全性是每个系统的核心。无论是智能家居、医疗设备还是工业自动化,每个设备都需要确保数据的安全性和完整性。对于许多应用来说,使用高级的微控制器或处理器可能是不切实际的,因为它们可能会增加成本…...
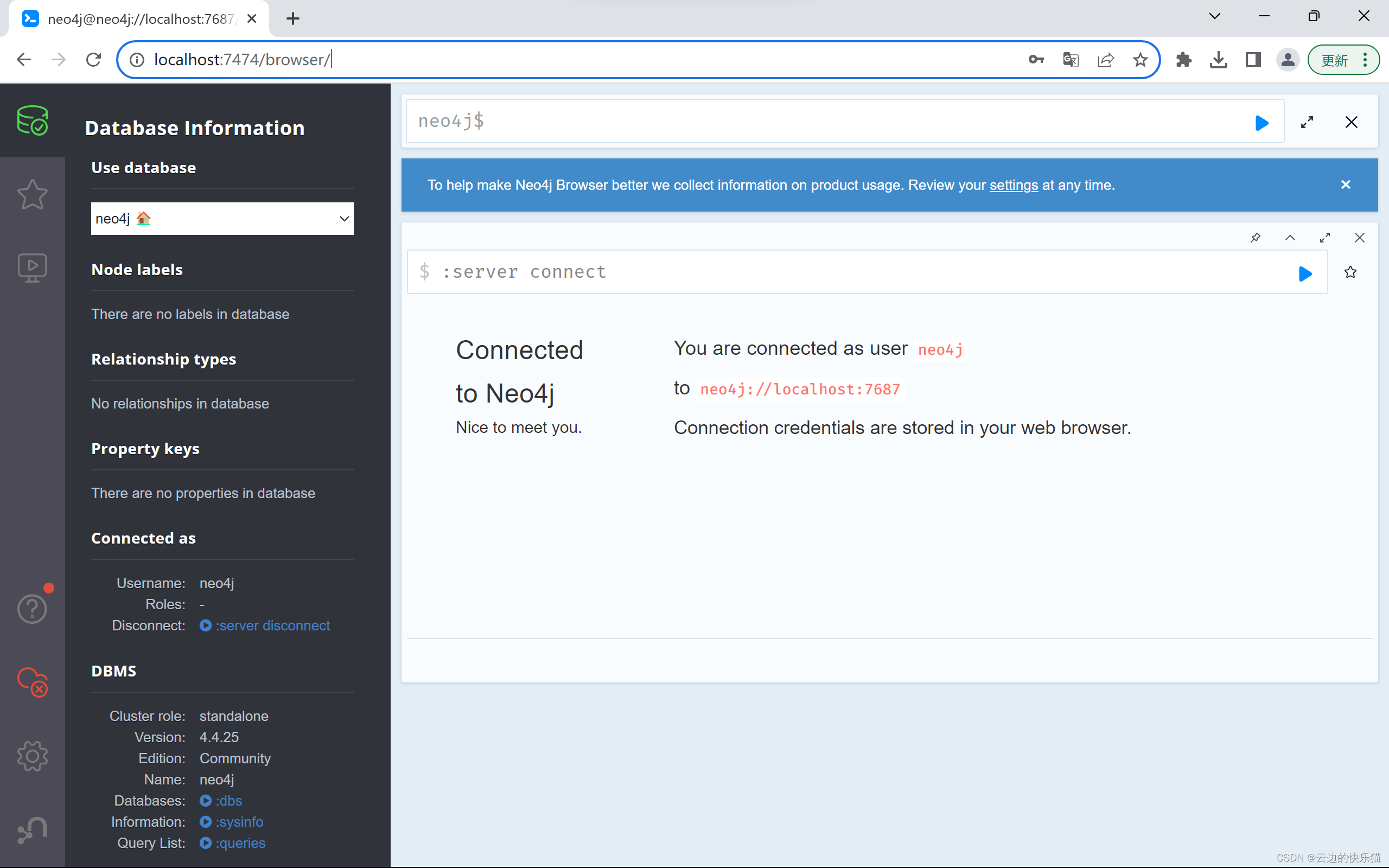
neo4j下载安装配置步骤
目录 一、介绍 简介 Neo4j和JDK版本对应 二、下载 官网下载 直接获取 三、解压缩安装 四、配置环境变量 五、启动测试 一、介绍 简介 Neo4j是一款高性能的图数据库,专门用于存储和处理图形数据。它采用节点、关系和属性的图形结构,非常适用于…...

【机组】计算机系统组成课程笔记 第二章 计算机中的信息表示
2.1 无符号数和有符号数 2.1.1 无符号数 没有符号的数,其实就是非负数。在计算机中用字节码表示,目前最常用的是八位和十六位的。 2.1.2 有符号数 将正负符号数字化,0代表 ,1代表 - ,并把代表符号的数字放在有效数…...
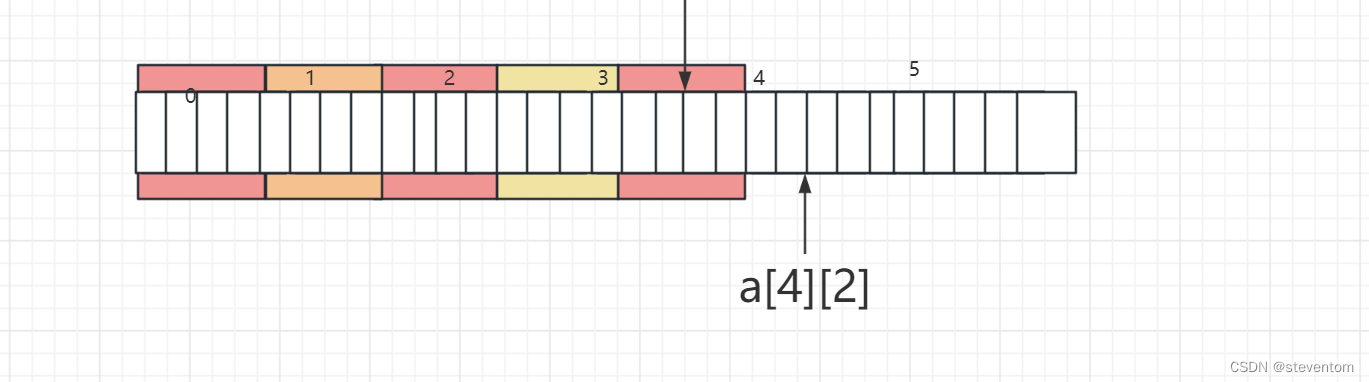
指针笔试题详解
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.前言 2.指针题写出下列程序的结…...

MySQL 日志管理、备份与恢复
目录 1 数据备份的重要性 2 MySQL 日志管理 3 备份类型 3.1 数据备份的分类 3.2 备份方式比较 3.3 合理值区间 3.4 常见的备份方法 4 MySQL 完全备份与恢复 4.1 MySQL 完全备份 5 mysqldump 备份与恢复 5.1 MySQL 完全恢复 6 MySQL 增量备份与恢复 6.1 MySQL 增量…...
vtk- 数据类型(一) 三角链实例代码
三角链实例代码 #include <iostream> #include <string> #include <regex> #include "tuex.h" #include "vtkCylinderSource.h" #include "vtkPolyDataMapper.h" #include "vtkActor.h" #include "vtkRendere…...
Git大全
目录 一、Git概述 1.1Git简介 1.2Git工作流程图 1.3查看Git的版本 1.4 Git 使用前配置 1.5为常用指令配置别名(可选) 1.5.1打开用户目录,创建 .bashrc 文件 1.5.2在 .bashrc 文件中输入如下内容: 1.5.3打开gitBash,执行…...

Touch命令使用指南:创建、更新和修改文件时间戳
文章目录 教程:touch命令的使用指南一、介绍1.1 什么是touch命令?1.2 touch命令的作用1.3 touch命令的语法 二、基本用法2.1 创建新文件2.2 更新文件时间戳2.3 创建多个文件2.4 修改文件访问时间2.5 修改文件修改时间2.6 修改文件创建时间 三、高级用法3…...

Windows开启 10 Telnet
在Windows 10中,Telnet客户端默认是不安装的。要在Windows 10上使用Telnet客户端,您需要手动启用它。以下是启用Telnet客户端的步骤: 打开控制面板。您可以通过在开始菜单中搜索"控制面板"来找到它。在控制面板中,选择…...

高教杯数学建模A题程序设计要点与思路
2023 年是我最后一次参加 高教杯大学生数学建模竞赛 以后不会再参加了(大四参加意义不太,研究生有研究生的数学建模大赛) 很遗憾 由于各种原因 我们没有能够完成赛题2022 年 美赛 2022年 Mathor Cup 2022 年国赛 2022 亚太杯 2023年 美赛 202…...

Spring Boot的新篇章:探索2.0版的创新功能
文章目录 引言1. Spring Boot 2.0的响应式编程2. 自动配置的改进3. Spring Boot 2.0的嵌入式Web服务器4. Spring Boot 2.0的Actuator端点5. Spring Boot 2.0的Spring Data改进6. Spring Boot 2.0的安全性增强7. Spring Boot 2.0的监控和追踪8. Spring Boot 2.0的测试改进结论 &…...
5、SpringBoot_热部署
六、热部署 1.热部署概述 概述:程序更改后,不需要重新启动服务器也能够实现动态更新 springboot 项目如何实现热部署? tomcat 已经内置到项目容器中了希望tomcat监听外部程序变化通过新建一个程序来监控你代码的变化 2.依赖导入 依赖 <…...
【kohya】训练自己的LoRA模型
文章目录 序言准备环境准备图片处理图片下载kohya_ss代码修改pyvenv.cfg启动界面访问地址生成字幕准备训练的文件夹配置训练参数开始训练遇到的问题: 序言 在把玩stable diffusion的webUI和comfyUI后,思考着自己也微调一个个性化风格的checkpoint、LyCO…...
[尚硅谷React笔记]——第1章 React简介
目录: 第1章 React简介 React的基本使用:虚拟DOM的两种创建方式: 使用jsx创建虚拟DOM使用js创建虚拟DOM(一般不用)虚拟DOM与真实DOM:React JSX:JSX练习:模块与组件、模块化与组件化的理解 模块组件模块化组件化 第1章 React简介 中文官网: …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
