2023 “华为杯” 中国研究生数学建模竞赛(E题)深度剖析|数学建模完整代码+建模过程全解全析

问题一
血肿扩张风险相关因素探索建模
思路:
根据题目要求,首先需要判断每个患者是否发生了血肿扩张事件。根据定义,如果后续检查的血肿体积比首次检查增加≥6 mL或≥33%,则判断为发生了血肿扩张。
具体判断步骤:
(1) 从表1中提取每个患者的入院首次影像检查流水号;
(2) 根据流水号在附表1中查找对应首次检查的时间点;
(3) 计算发病到首次检查的时间间隔;
(4) 在表2中找到每个随访时间点的血肿体积;
(5) 依次计算相邻两次检查血肿体积变化量和变化百分比;
(6) 如果变化量≥6 mL 或变化百分比≥33%,则记为发生血肿扩张,记录下血肿扩张发生的时间点。
3.使用logistic回归建模,以是否发生血肿扩张作为目标变量,个人史、疾病史和首次影像特征作为自变量,建立预测模型。
目标变量: Y = 是否发生血肿扩张(1是,0否)
自变量: X1, X2, …, Xn(个人史、疾病史等)
建模公式: P(Y=1|X) = 1 / (1+e^-(b0+b1X1+…+bnXn))
4.使用训练集拟合logistic回归模型
(1) 将训练集的个人史、疾病史和首次影像特征整理为自变量X
(2) 将训练集的血肿扩张标记(1或0)作为目标变量Y
(3) 将自变量X和目标变量Y喂入logistic回归模型进行拟合
(4) 使用最大似然估计获得变量系数b0, b1, …, bn
(5) 得到拟合后的模型:
P(Y=1|X) = 1 / (1+e^-(b0+b1X1+…+bnXn))
5.用拟合好的模型对测试集进行预测
(1) 对测试集数据进行同样的特征工程,提取自变量X
(2) 将测试集的自变量X代入上面得到的模型中
(3) 计算每个样本的血肿扩张概率P(Y=1|X)
(4) 如果P(Y=1|X) ≥ 0.5,则预测该样本发生了血肿扩张
(5) 计算模型在测试集上的评估指标,如AUC等
(6) 根据变量系数的大小分析变量与血肿扩张的相关性
import pandas as pd
from sklearn.linear_model import LogisticRegression# 读取表1和表2中的数据
table1 = pd.read_excel('表1.xlsx')
table2 = pd.read_excel('表2.xlsx')# 将表1和表2进行合并
data = pd.merge(table1, table2, on='ID')# 提取需要的特征
features = ['age', 'gender', 'history', ...] # 获得每个患者的首次影像时间和血肿体积
first_scan = data.groupby('ID')['time'].min()
first_volume = data[data['time'] == first_scan]['HM_volume']
代码主要步骤包括:
读取和合并表格
特征工程
标记目标变量
划分训练集和测试集
模型训练和预测
输出结果
此处我们使用xgboost训练模型:
主要步骤为:
导入xgboost
设置xgboost的参数:
eta:学习率
max_depth:树的最大深度
objective:二分类的逻辑回归
eval_metric:评估指标设为AUC
将训练数据转换为DMatrix格式
使用xgboost训练模型
将测试数据也转为DMatrix格式
用训练好的模型进行预测
输出结果
XGBoost是一个流行且高效的树模型库,可以提取数据的复杂特征关系。
相比逻辑回归,XGBoost可处理各种类型的特征,也便于调参优化模型。
问题二
血肿周围水肿的发生及进展建模,并探索治疗干预和水肿进展的关联关系。
构建水肿体积随时间变化的模型
可以使用 Curve Fitting 的方法,以时间为自变量,水肿体积为目标变量,拟合出水肿体积随时间的曲线模型:
V E D = f ( t ) V_{ED} = f(t) VED=f(t)
其中, V E D V_{ED} VED表示水肿体积, t t t表示时间。
可以试用不同的曲线拟合方法,如线性回归、多项式回归、局部加权回归等。
计算患者真实值与拟合曲线的残差
对第i个样本:
r i = V E D i − f ( t i ) r_i = V_{ED_i} - f(t_i) ri=VEDi−f(ti)
其中, V E D i V_{ED_i} VEDi为第i个样本的真实水肿体积, f ( t i ) f(t_i) f(ti)为对应时间点上的拟合值。
划分患者亚组,拟合各亚组的水肿体积曲线
可以使用聚类算法如K-means对患者进行分群,然后对每一群体单独拟合曲线。
分析不同治疗对水肿演变的影响
可以将治疗方法作为类别特征,构建不同的曲线模型,然后比较模型效果。
也可以通过统计学方法(如t检验)比较不同治疗组水肿体积变化的差异。
分析三者之间的关系
可以采用相关性分析等统计学方法探索血肿体积、水肿体积和治疗之间的关系。
也可以构建包含三者作为特征的预测模型,通过分析系数等来发现三者之间的关联。
具体来说,相关性分析法
(1) 计算每个样本的血肿体积、水肿体积和各种治疗方式的 0/1 表示
(2) 使用 Pearson 相关系数计算血肿体积和水肿体积的线性相关性
(3) 使用 Spearman 秩相关系数计算血肿体积与各治疗方法的秩相关性
(4) 使用 Spearman 秩相关系数计算水肿体积与各治疗方法的秩相关性
(5) 比较不同系数的大小,分析三者之间的相关程度
建模法
(1) 将血肿体积、水肿体积作为连续特征,治疗方法作为分类特征
(2) 构建回归模型,以水肿体积为目标变量,血肿体积和治疗作为自变量
(3) 训练模型,得到各变量的系数
(4) 比较各治疗类别的系数,看其对水肿体积的影响效果
(5) 通过变量的显著性检验,选择关键的影响因素
(6) 分析模型总体表现,评估各变量的解释能力
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.cluster import KMeans# 读取数据
data = pd.read_excel('table2.xlsx') # 特征工程:提取时间和水肿体积
X = data[['time']]
y = data[['ED_volume']]# 构建线性回归模型
lr = LinearRegression()# 训练模型
lr.fit(X, y)# 获取拟合的系数
print('模型Slope:', lr.coef_)
print('模型Intercept:', lr.intercept_)# 预测水肿体积
y_pred = lr.predict(X)
问题三
出血性脑卒中患者预后预测及关键因素探索
1.基于首次影像结果预测预后
使用回归模型,以90天mRS评分为目标变量,个人史、疾病史和首次影像特征为自变量:
m R S = w 0 + w 1 x 1 + . . . + w n x n mRS = w_0 + w_1x_1 + ... + w_nx_n mRS=w0+w1x1+...+wnxn
其中, m R S mRS mRS为预后评分, x i x_i xi为各特征, w i w_i wi为对应的权重系数。
可以试用线性回归、LASSO回归等算法。
2.基于全部影像结果预测预后
同上,不仅使用首次影像,还结合后续各时间点的影像特征,构建回归模型进行预测。
3.分析关键影响因素
通过分析各变量的权重 w i w_i wi,确定对 m R S mRS mRS影响最大的特征。
使用统计检验分析不同特征对 m R S mRS mRS的显著影响。
采用则特征选择的方法(如RFE),选择关键特征。
将无关特征删除后,观察模型评分的变化。
具体来说,
1)建模算法的选择
可以尝试线性回归、LASSO回归、GBDT等多种算法
比较不同算法的误差、过拟合情况,选择较优算法
调参优化模型,提升准确率
2)特征工程
处理缺失值:删除/填充
编码类别特征:One-hot 编码
标准化连续特征:去均值和方差归一化
提取时间序列特征:趋势、周期性等
采用 PCA 等方法降维
3)模型评估
划分训练集、验证集、测试集
多次交叉验证,观察方差
计算 RMSE、R2、MAE 等评价指标
绘制学习曲线,检查过拟合问题
4)关键因素分析
计算特征影响力,排序筛选
通过添加/删除特征,比较模型效果变化
使用统计学检验(t-test等)判断显著性
采用正则化方法自动特征筛选
分析特征在不同亚群中的效果
4.提出建议
对具有显著影响的特征,分析临床意义,给出干预建议。
对预后良好和预后不良的患者组,进行对比分析,找出影响因素的差异。
代码:
# 导入需要的库
import pandas as pd
from sklearn.linear_model import Lasso
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt# 读取数据
data = pd.read_csv('data.csv')# 特征工程
X = data[['age', 'gender', 'treatment', 'image_features']]
y = data['mRS']# 拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2020)# Lasso回归
model = Lasso()# 使用网格搜索找到最优参数
from sklearn.model_selection import GridSearchCV
params = {'alpha': [0.001, 0.01, 0.1, 1]}
gs = GridSearchCV(model, params, scoring='neg_mean_squared_error', cv=5)
gs.fit(X_train, y_train)
print('最优参数:', gs.best_params_)
model = gs.best_estimator_#见完整版
完整版的思路看看我的回答哈~
(5 封私信 / 2 条消息) 如何评价2023数学建模研赛? - csdn
相关文章:

2023 “华为杯” 中国研究生数学建模竞赛(E题)深度剖析|数学建模完整代码+建模过程全解全析
问题一 血肿扩张风险相关因素探索建模 思路: 根据题目要求,首先需要判断每个患者是否发生了血肿扩张事件。根据定义,如果后续检查的血肿体积比首次检查增加≥6 mL或≥33%,则判断为发生了血肿扩张。 具体判断步骤: (1) 从表1中提取每个患者的入院首次影像检查…...
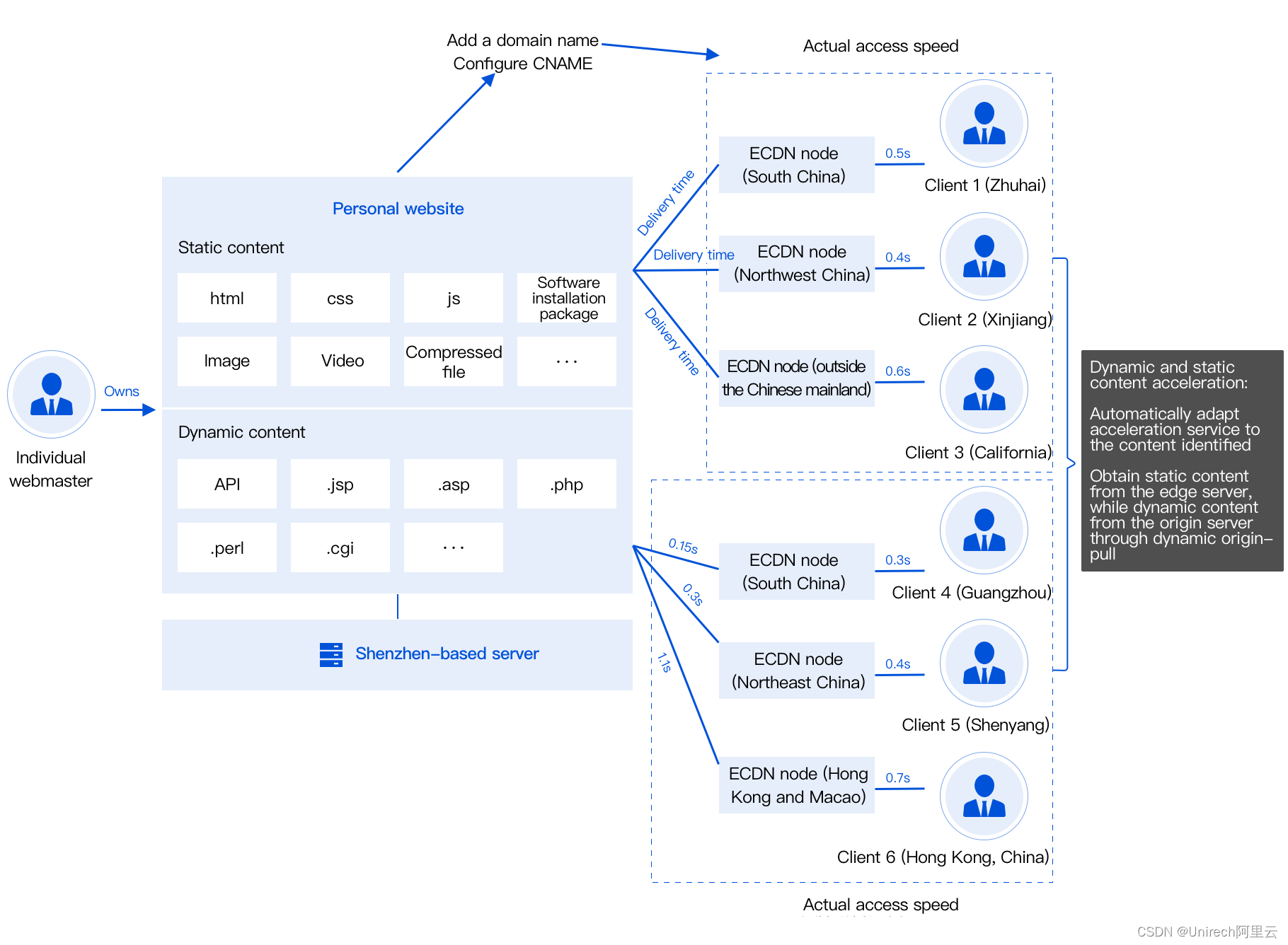
【腾讯云国际站】CDN内容分发网络特性介绍
为什么使用腾讯云国际站 CDN 内容分发网络? 当用户直接访问源站中的静态内容时,可能面临的体验问题: 客户离服务器越远,访问速度越慢。客户数量越多,网络带宽费用越高。跨境用户访问体验较差。 腾讯云国际站CDN 如何改…...

【工业机器人视觉】
工业机器人视觉 工业机器人的定位、抓取任务是工业生产线上一项重要的应用,一般通过预先示教的方式让机器人执行预定的指令动作。但是,一旦工件的状态发生改变时,机器人便无法完成工作任务。区别:就像人睁眼走直线和闭眼走直线。…...
)
跨域(浏览器)
跨域问题 是前端开发中常遇到的一个挑战。由于浏览器的同源策略限制,前端在发起异步请求时会受到限制,只能向相同源(域名、协议和端口号都相同)的服务器发送请求。当请求的目标服务器与当前页面的源不一致时,就会触发…...

Leetcode 2866. Beautiful Towers II
Leetcode 2866. Beautiful Towers II 1. 解题思路2. 代码实现 题目链接:2866. Beautiful Towers II 1. 解题思路 这一题其实思路上还是比较明显的,就是一个单调数组的问题,问题在于说如果具体去设计这个单调数组。 我们从题目出发&#x…...

电脑C盘爆红怎么办?(小白篇)
文章目录 前言:1、清理临时和系统文件2、更改电脑默认软件安装位置3、微信、QQ文件存储路径放在其它盘4、卸载一些不常用的软件彩蛋 前言: C盘作为电脑的系统盘,如果出现爆满或者剩余空间很小整个C盘变红,这样会导致电脑系统运行…...

Office Xml 2003转XLSX
一、使用到的依赖包 1、xelem-3.1.jar 下载地址:管网下载地址 2、poi-3.17.jar 下载地址:https://mvnrepository.com/artifact/org.apache.poi/poi 二、实现方法 1、Xml2003公式转XLSX公式算法 (1)Xml2003函数格式 SUM(R[-1…...
)
skyWalking搭建(一)
title: “SkyWalking搭建(一)” createTime: 2021-07-27T14:34:2108:00 updateTime: 2021-07-27T14:34:2108:00 draft: false author: “name” tags: [“skywalking”] categories: [“java”] description: “测试的” 基于 docker 部署 skywalking 并实现 SpringBoot 全链路…...

Golang开发--sync.WaitGroup
sync.WaitGroup 是 Go 语言标准库中的一个并发原语,用于等待一组并发操作的完成。它提供了一种简单的方式来跟踪一组 goroutine 的执行状态,并在所有 goroutine 完成后恢复执行。 下面是关于 sync.WaitGroup 的实现细节的详细解释: 创建 Wa…...

Linux命令教程:使用cat命令查看和处理文件
文章目录 教程:使用cat命令在Linux中查看和处理文件1. 引言2. cat命令的基本概述3. 查看文件内容4. 创建文件5. 文件重定向和管道6. 格式化和编辑文件7. 实际应用示例7.1 使用cat命令浏览日志文件7.2 利用cat命令合并多个配置文件7.3 使用cat命令将文件内容发送到其…...
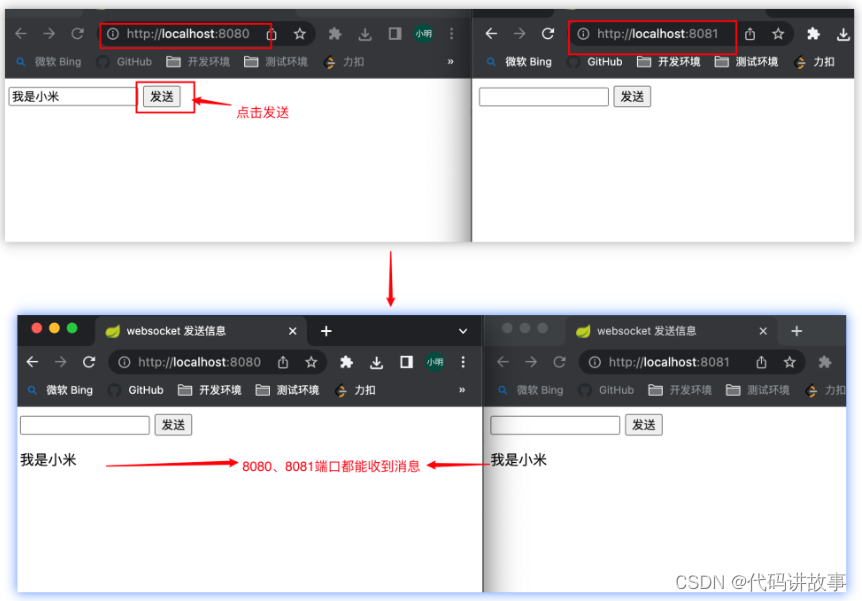
Websocket集群解决方案以及实战(附图文源码)
最近在项目中在做一个消息推送的功能,比如客户下单之后通知给给对应的客户发送系统通知,这种消息推送需要使用到全双工的websocket推送消息。 所谓的全双工表示客户端和服务端都能向对方发送消息。不使用同样是全双工的http是因为http只能由客户端主动发…...
)
科技的成就(五十一)
397、初等数论的不可解问题 1936 年 4 月,邱奇证明判定性问题不可解。33 岁的邱奇发表论文《初等数论的不可解问题》,运用λ演算给出了判定性问题一个否定的答案。λ演算是一套从数学逻辑中发展起来的形式系统,采用变量绑定和替换,…...
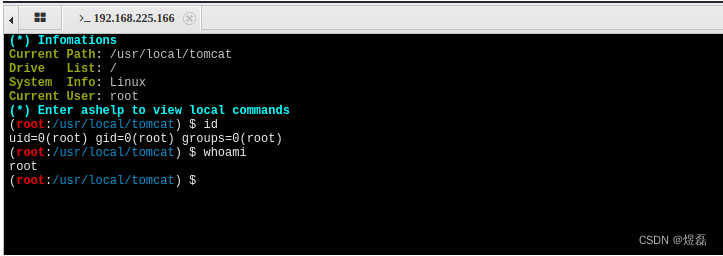
Tomcat8 任意写文件PUT方法 (CVE-2017-12615)
Tomcat 任意写文件PUT方法 (CVE-2017-12615) 文章目录 Tomcat 任意写文件PUT方法 (CVE-2017-12615)1 在线漏洞解读:2 版本影响3 环境搭建4 漏洞复现4.1 访问4.2 POC攻击点4.2.1 直接发送以下数据包,然后shell将被写入Web根目录。4.2.2 访问是否通,可以访…...

SAP服务器修改主机名操作手册
1、业务背景 SAP服务器P2V:虚拟化后的服务器主机名(或叫计算机名、设备名,hostname,下文同)会和原参照克隆的服务器主机名一样,若两台服务器处于同一网域,会出现域冲突,导致以下事故发生 (1)、使得原服务器出现掉域情况(DEV->CLN->PRD后台服务器访问失效) …...

【大数据】Doris 构建实时数仓落地方案详解(一):实时数据仓库概述
本系列包含: Doris 构建实时数仓落地方案详解(一):实时数据仓库概述Doris 构建实时数仓落地方案详解(二):Doris 核心功能解读Doris 构建实时数仓落地方案详解(三)&#…...
C++ list容器的实现及讲解
所需要的基础知识 对C类的基本了解 默认构造函数 操作符重载 this指针 引用 模板等知识具有一定的了解,阅读该文章会很轻松。 链表节点 template<class T>struct list_node{T _data;list_node<T>* _next;list_node<T>* _prev;list_node(const T&…...
前端项目练习(练习-002-NodeJS项目初始化)
首先,创建一个web-002项目,内容和web-001一样。 下一步,规范一下项目结构,将html,js,css三个文件放到 src/view目录下面: 由于html引入css和js时,使用的是相对路径,所以…...
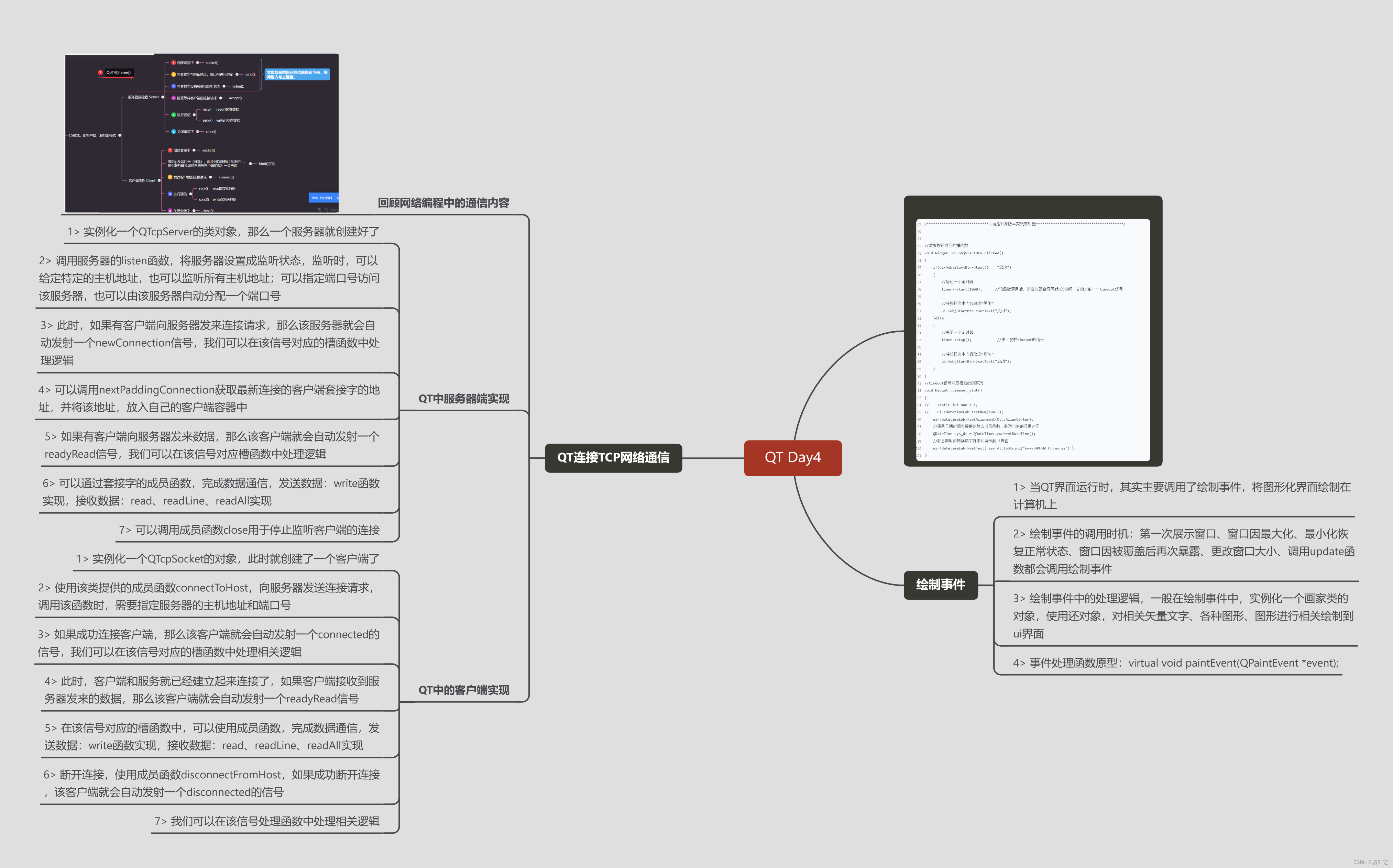
C++QT day11
绘制时钟 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPaintEvent>//绘制事件类 #include <QDebug>//信息调试类 #include <QPainter>//画家类 #include <QTimer>//定时器类 #include <QTime> #include &…...

Stable DIffusion 炫酷应用 | AI嵌入艺术字+光影光效
目录 1 生成AI艺术字基本流程 1.1 生成黑白图 1.2 启用ControlNet 参数设置 1.3 选择大模型 写提示词 2 不同效果组合 2.1 更改提示词 2.2 更改ControlNet 2.2.1 更改模型或者预处理器 2.2.2 更改参数 3. 其他应用 3.1 AI光影字 本节需要用到ControlNet,可…...

C#通过重写Panel改变边框颜色与宽度的方法
在C#中,Panel控件是一个容器控件,用于在窗体或用户控件中创建一个可用于容纳其他控件的面板。Panel提供了一种将相关控件组合在一起并进行布局的方式。以下是Panel控件的详细使用方法: 在窗体上放置 Panel 控件: 在 Visual Studio 的窗体设计器中,从工具箱中拖动并放置一…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
