洛谷 P5764 [CQOI2005]新年好
P5764 [CQOI2005]新年好
题目描述
重庆城里有 nnn 个车站,mmm 条双向公路连接其中的某些车站。每两个车站最多用一条公路连接,从任何一个车站出发都可以经过一条或者多条公路到达其他车站,但不同的路径需要花费的时间可能不同。在一条路径上花费的时间等于路径上所有公路需要的时间之和。
佳佳的家在车站 111,他有五个亲戚,分别住在车站 a,b,c,d,ea,b,c,d,ea,b,c,d,e。过年了,他需要从自己的家出发,拜访每个亲戚(顺序任意),给他们送去节日的祝福。怎样走,才需要最少的时间?
输入格式
第一行:n,mn,mn,m,分别为车站数目和公路的数目。
第二行:a,b,c,d,ea,b,c,d,ea,b,c,d,e,分别为五个亲戚所在车站编号。
以下 mmm 行,每行三个整数 x,y,tx,y,tx,y,t,为公路连接的两个车站编号和时间。
输出格式
仅一行,包含一个整数 TTT,为最少的总时间。保证 T≤109T\le 10^9T≤109。
样例 #1
样例输入 #1
6 6
2 3 4 5 6
1 2 8
2 3 3
3 4 4
4 5 5
5 6 2
1 6 7
样例输出 #1
21
提示
对于 40%40\%40% 的数据,有 1≤n≤5001≤n≤5001≤n≤500,1≤m≤20001≤m≤20001≤m≤2000。
对于 100%100\%100% 的数据,有 1≤n≤500001≤n≤500001≤n≤50000,1≤m≤1000001≤m≤1000001≤m≤100000,1≤a,b,c,d,e≤n1\le a,b,c,d,e≤n1≤a,b,c,d,e≤n,1≤x,y≤n1≤x,y≤n1≤x,y≤n,1≤t≤100001≤t≤100001≤t≤10000。
思路
起点确定,所到达的点集有限,且大小固定为5,非常小,于是我们可以爆搜访问点集中每个点的顺序,也就是全排列。在爆搜过程中我们需要知道当前点xxx到要访问的点yyy的最短距离,最短距离可以用很多算法求解,本题数据量可知所给出的图为稀疏图,范围比较大,首选堆优化的Dijkstra算法,最短距离需要预先处理,这样在爆搜的过程中离线查询即可。本题的存图方式比较常规,但是记录最短路有些讲究,我们需要开一个二维数组dist[7][N]dist[7][N]dist[7][N],dist[i][j]dist[i][j]dist[i][j]表示start[i]start[i]start[i]到jjj的最短路,这样记录最短路的话,我们可以枚举会访问六个点到其他点的最短路。
参考代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 50010, M = 200010, INF = 0x3f3f3f3f;int n, m, res;
int start[7], dist[7][N];
int h[N], e[M], ne[M], w[M], idx;
bool st[N], vis[6];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}void dijkstra(int sr, int dist[]) {memset(st, 0, sizeof st);priority_queue<PII, vector<PII>, greater<PII>> que;dist[sr] = 0;que.push({0, sr});while(que.size()) {auto tt = que.top(); que.pop();if(st[tt.y]) continue;st[tt.y] = true;for(int i = h[tt.y]; ~i; i = ne[i]) {int j = e[i];if(dist[j] > tt.x + w[i]) {dist[j] = tt.x + w[i];que.push({dist[j], j});}}}
}void dfs(int u, int cost, int p) {if(u == 6) {res = min(res, cost);}if(cost > res) return ;for(int i = 2; i <= 6; i ++) {if(!vis[i]) {vis[i] = true;dfs(u + 1, cost + dist[p][start[i]], i);vis[i] = false;}}
}int main() {scanf("%d%d", &n, &m);start[1] = 1;for(int i = 2; i <= 6; i ++) scanf("%d", &start[i]);memset(h, -1, sizeof h);while(m --) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}memset(dist, 0x3f, sizeof dist);for(int i = 1; i <= 6; i ++) dijkstra(start[i], dist[i]);res = INF;dfs(1, 0, 1);printf("%d\n", res);return 0;
}
疑问
有疑问欢迎私信或者评论,看到消息会解答
相关文章:

洛谷 P5764 [CQOI2005]新年好
P5764 [CQOI2005]新年好 题目描述 重庆城里有 nnn 个车站,mmm 条双向公路连接其中的某些车站。每两个车站最多用一条公路连接,从任何一个车站出发都可以经过一条或者多条公路到达其他车站,但不同的路径需要花费的时间可能不同。在一条路径上…...

【自然语言处理】主题建模:BERTopic(实战篇)
主题建模:BERTopic(实战篇)BERTopic 是基于深度学习的一种主题建模方法。201820182018 年底,Devlinetal.Devlin\ et\ al.Devlin et al. 提出了 Bidirectional Encoder Representations from Transformers (BERT)[1]^{[1]}[1]。BER…...

k8s学习笔记
目录 一、安装前准备 二、安装 1、安装kubelet、kubeadm、kubectl 2、使用kubeadm引导集群 1、下载各个机器需要的镜像 2、初始化主节点 3、加入node节点 3、部署dashboard 1、主节点安装 2、设置访问端口 3、创建访问账号 4、令牌访问获取token 三、实战 1、资源创…...

web自动化测试入门篇05——元素定位的配置管理
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...
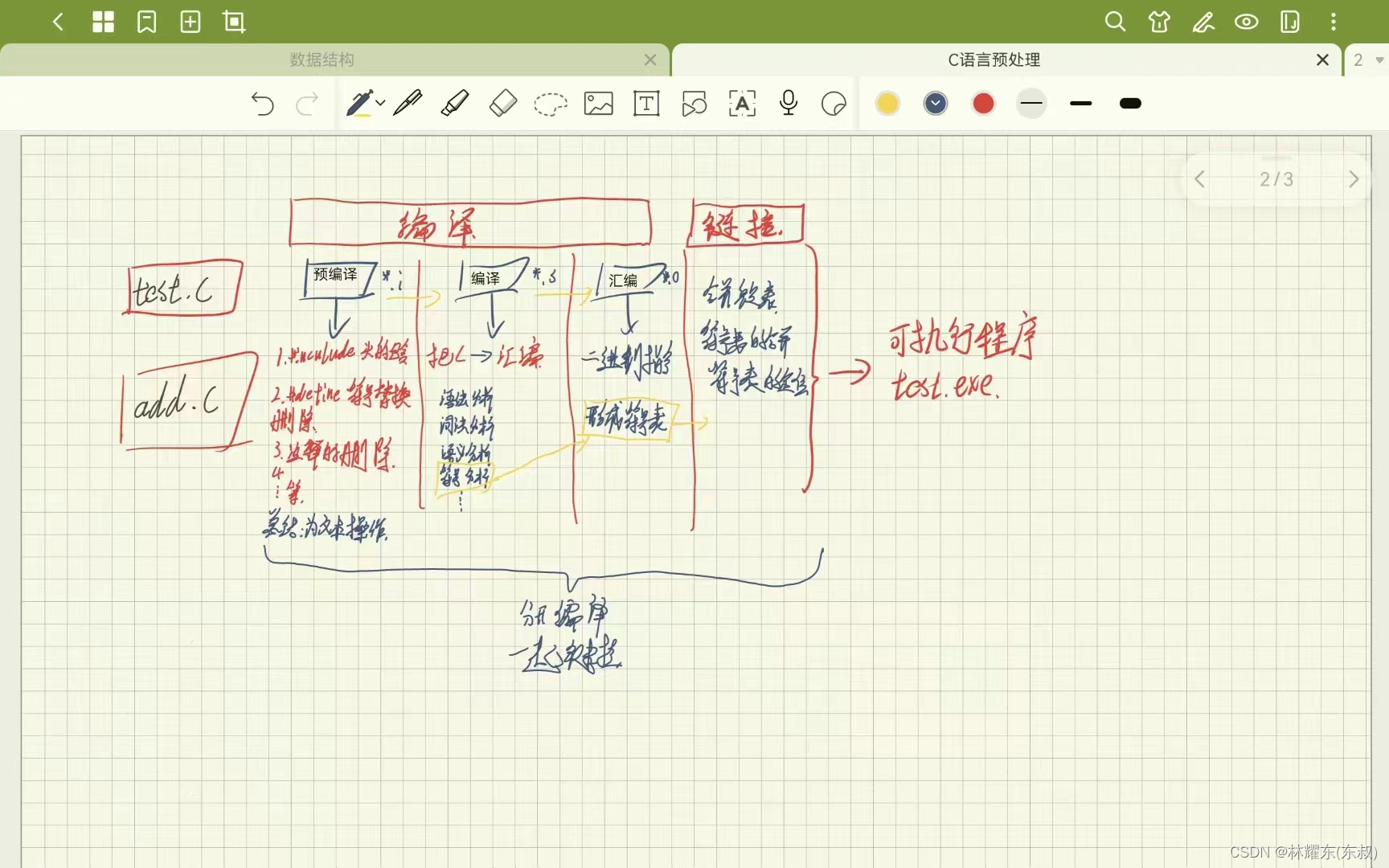
C语言预处理
文章目录 目录 文章目录 前言 一、程序编译的过程 二、编译阶段 1.预处理(*.i) 2.编译(*.s) 3.汇编(*.o) 4.链接 总结 前言 提示:使用vs code(gcc编译器)与vs2022来演示c语言的预处理 提示:以下是本篇文章正文内容,下面…...
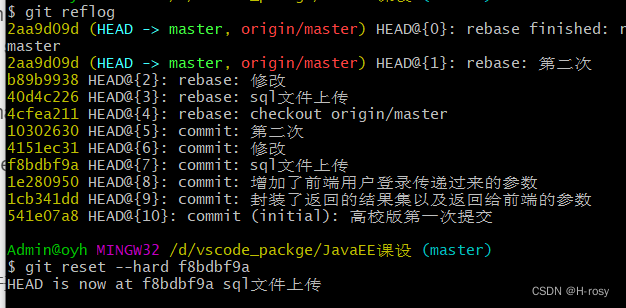
git报错大全,你将要踩的坑我都帮你踩了系列
使用git push -u origin master报下面的错: 使用git push -u origin master报下面的错: Updates were rejected because the remote contains work that you do not have locally,This is usually caused by another repository pushing to …...
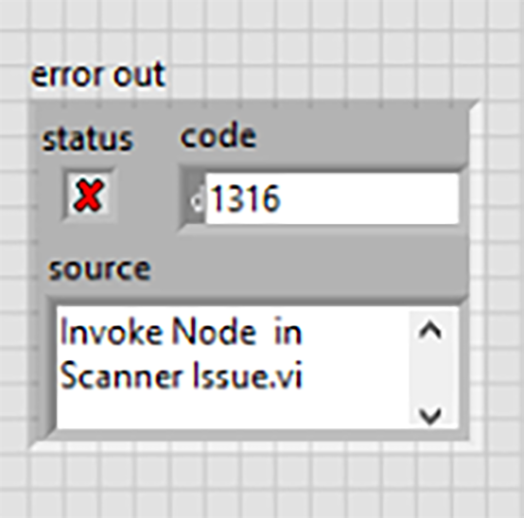
LabVIEW中使用.NET方法时出现错误1316
LabVIEW中使用.NET方法时出现错误1316为什么不能调用带有泛型参数的方法?LabVIEW不支持哪些.NET功能?为什么会收到以下错误:发生此错误的原因是正在调用LabVIEW中不支持的.NET功能。有关解决方法,请参阅“其他信息”部分。可以在下…...

HTTP2.0 相比 HTTP1.0、HTTP1.1 有哪些重大改进?值得升级更换吗?
目录 HTTP1.0 HTTP1.1 HTTP2.0 主要特性对比 HTTP发展历史 HTTP2解决的问题 HTTP1.0 HTTP1.1 HTTP2.0...
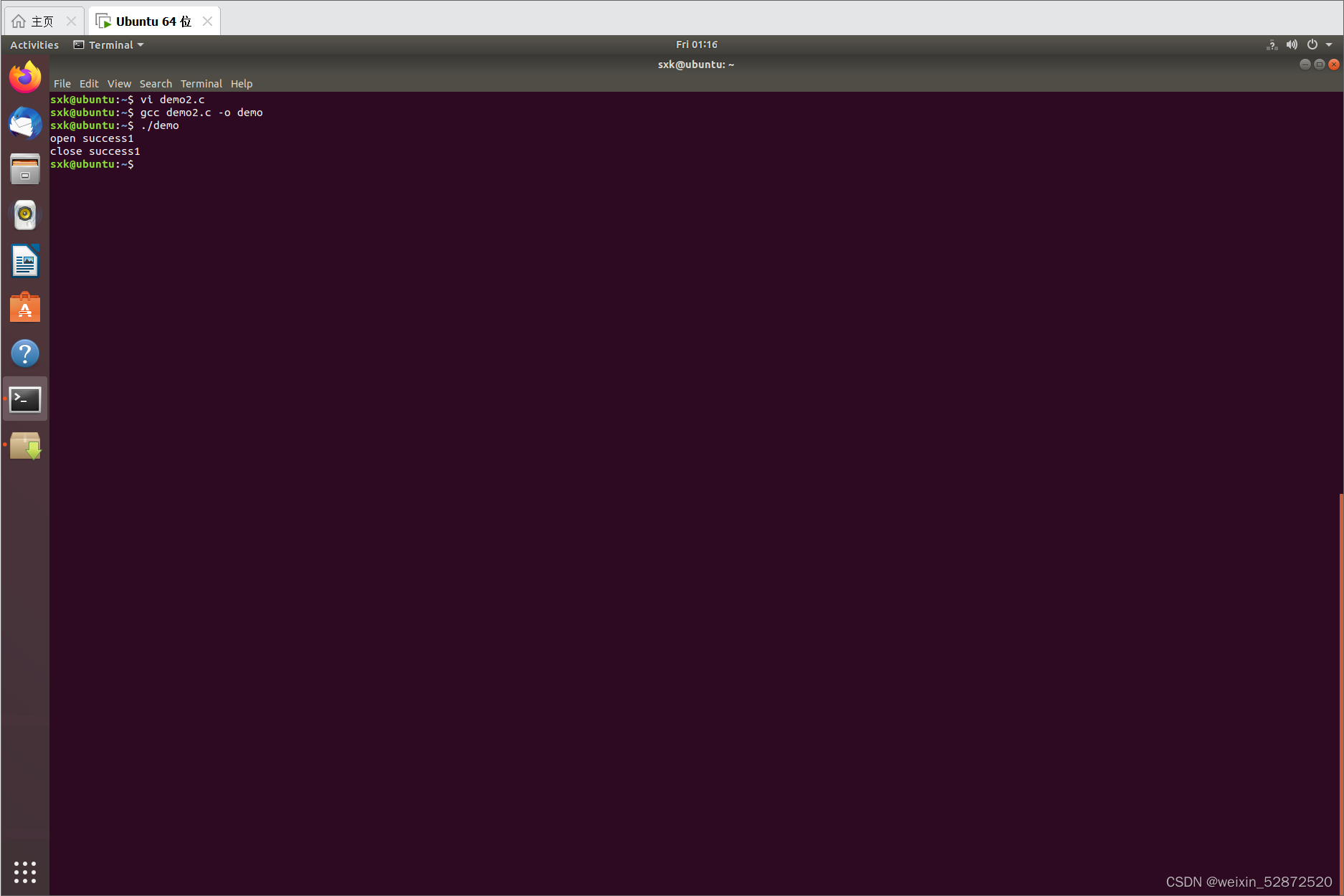
九、Linux文件 - fopen函数和fclose函数讲解
目录 1.fopen函数 2.fclose函数 3.fopen函数和fclose实战 1.fopen函数 fopen fwrite fread fclose ...属于标准C库 include <stdio.h> standard io lib open close write read 属于Linux系统调用 可移植型:fopen > open(open函数只在嵌入…...

轨迹预测算法vectorNet调研报告
前言 传统的行为预测方法是规则的,基于道路结构的约束生成多个行为假设。最近,很多基于学习的预测方法被提出。他们提出了对于不同行为假设的进行概率解释的好处,但是需要重构一个新的表示来编码地图和轨迹信息。有趣的是,虽然高精…...
基于STM32设计的避障寻迹小车
一、前言 1.1 项目背景 根据美国玩具协会在一项研究中,过去几年全球玩具销售增长与GDP的世界平均水平大致相同。但全球玩具市场的内部结构已经占据了巨大的位置变化:传统玩具的市场份额正在下降,高科技电子玩具正在蓬勃发展。全球玩具市场的…...

【视觉检测】使用opencv编写一个图片缺陷检测流程
1. 导入必要的库,如OpenCV,NumPy等。 2. 使用OpenCV读取图像,并将其转换为灰度图像。 3. 使用OpenCV的Canny边缘检测算法检测图像中的边缘。 4. 使用OpenCV的Hough变换算法检测图像中的线条。 5. 使用OpenCV的模板匹配算法检测图像中的缺…...

3.Dockerfile 定制镜像
3. Dockerfile 定制镜像 从上一节的docker commit的学习中,我们可以了解到,镜像的定制实际上就是定制每一层所添加的配置、文件等信息,但是命令毕竟只是命令,每次定制都得去重复执行这个命令,而且还不够直观ÿ…...

Web基础与HTTP协议
Web基础与HTTP协议一、Web基础与HTTP概述1、域名概念二、域名服务与域名注册1、域名定义2、域名服务三、网页访问(http、https)1、网页概述2、网页的基本标签四、Web1、Web概述2、Web1.0 Web2.0五、HTTP协议概述1、HTTP协议简介2、HTTP协议请求总结一、W…...
【化学试剂】endo-BCN-PEG4-Pomalidomide,(1R,8S,9S)-双环[6.1.0]壬-四聚乙二醇-泊马度胺纯度95%+
一、基础产品数据(Basic Product Data):CAS号:N/A中文名:(1R,8S,9S)-双环[6.1.0]壬-四聚乙二醇-泊马度胺英文名:endo-BCN-PEG4-Pomalidomide二、详细产品数据(Detailed Product Data)…...
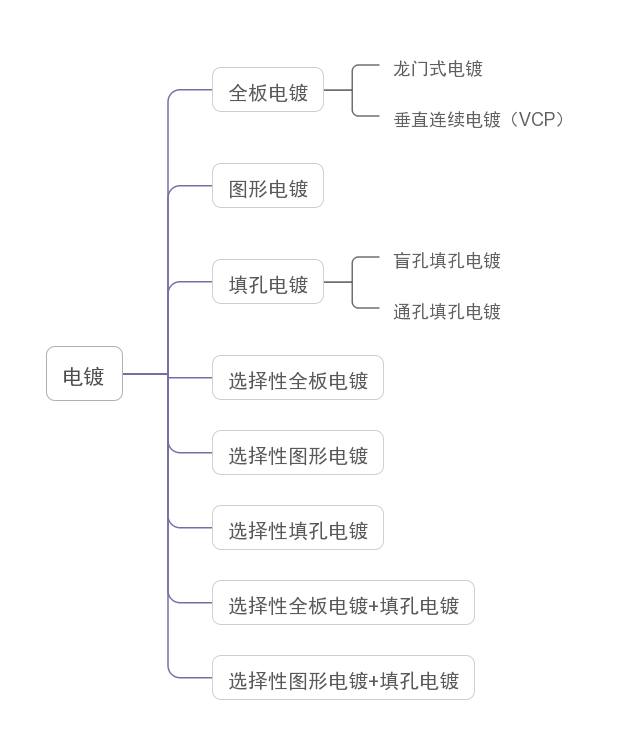
全板电镀与图形电镀,到底有什么区别?
衔接上文,继续为朋友们分享普通单双面板的生产工艺流程。 如图,第四道主流程为电镀。 电镀的目的为: 适当地加厚孔内与板面的铜厚,使孔金属化,从而实现层间互连。 至于其子流程,可以说是非常简单&#x…...
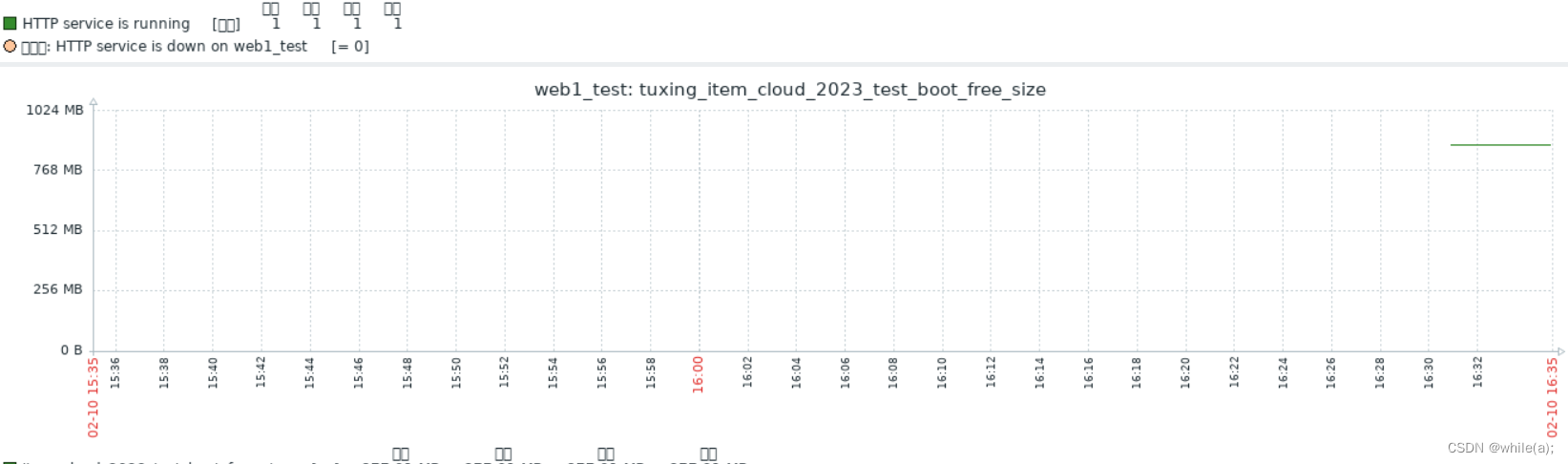
Zabbix 构建监控告警平台(二)--
Apache监控示例(图形监控)模板TemplateZabbix Items 1.Apache监控示例(图形监控) 1.1创建主机组 在“配置”->“主机群组”->“创建主机群组” 填入组名“webserver_test” 创建完成之后可以在“配置”->"主机群组&…...

开学季,关于校园防诈骗宣传,如何组织一场微信线上答题考试
开学季,关于校园防诈骗宣传,如何组织一场微信线上答题考试如何组织一场微信线上答题考试在线考试是一种非常节约成本的考试方式,考生通过微信扫码即可参加培训考试,不受时间、空间的限制,近几年越来越受企事业单位以及…...
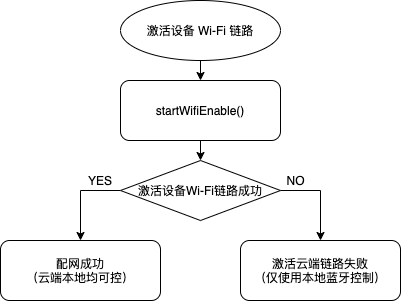
蓝牙单点技术实现路径介绍
本文主要介绍蓝牙设备与手机一对一相连的 蓝牙单点 技术。 准备工作 系统要求:蓝牙使用需要安卓 4.3 以及以上版本,智能生活 App SDK 从安卓 4.4 开始支持。Manifest 权限: <uses-permission android:name"android.permission.ACCE…...

Ubuntu22.04 用 `hwclock` 或 `timedatectl` 来设置RTC硬件时钟为本地时区
Ubuntu22.04用 hwclock 或 timedatectl 来设置硬件时区为本地时区 可以用hwclock命令 sudo hwclock --localtime --systohc👆效果等同👇 , --localtime的简写是-l ; --systohc的简写是-w sudo hwclock -l -w也可以用timedatectl命令 👆效果…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
