刷题记录:牛客NC25078[USACO 2007 Ope S]City Horizon
传送门:牛客
题目描述:
Farmer John has taken his cows on a trip to the city! As the sun sets, the cows gaze at the city horizon and
observe the beautiful silhouettes formed by the rectangular buildings.
The entire horizon is represented by a number line with N (1 ≤ N ≤ 40,000) buildings. Building i's silhouette has
a base that spans locations Ai through Bi along the horizon (1 ≤ Ai < Bi ≤ 1,000,000,000) and has height Hi (1 ≤
Hi ≤ 1,000,000,000). Determine the area, in square units, of the aggregate silhouette formed by all N buildings.
输入:
4
2 5 1
9 10 4
6 8 2
4 6 3
输出;
16
经典的多个矩形覆盖求总面积问题.需要使用扫描线算法进行解决.
对于扫描线算法,网上有大量博客对此进行讲解,此处就不在赘述了
为各位在提供一个有关这道题的另一种题面(不要换了题面就不会做了):
有一个数列,初始值均为0,他进行N次操作,每次将数列[ai,bi)这个区间中所有比Hi小的数改为Hi,他想知道N次操作后数列中所有元素的和。
看了这个题面有没有感觉扫描线的一些神奇之处??感觉有点积分的思想在那里了,反正我刚开始看到这道题(当我学完扫描线之后),我当时仍然是不知道怎么做的,根本就没有往扫描线那里想,还在想该怎么维护这道题.
优化&巧妙的想法:对于这种只需要区间[1,n]的维护值来说,我们建立线段树的时候可以不使用pushdown(因为我们根本不需要关注子节点是怎么样的),在子节点pushup的时候将父节点对子节点的lazy加上即可.
注意,此方法在我看来并不具有很强的意义,虽然省去了对子节点的维护,码量减少了,但是因为这种方式大大的修改了模板,会导致出现一写奇奇怪怪的错误甚至思维上的混乱,但是在平时可以挑战一下,这样改变常规的做法可以大大增强自己对线段树的理解
下面是具体的代码部分(标准版维护版):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,cov,lazy;
}tree[maxn*8];
struct Line{int l,r,y,cate;bool operator < (const Line &rhs) const {return y<rhs.y;}
}line[maxn];
int n;vector<int>v;
int Get_id(int x) {return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;if(l==r) return ;int mid=(l+r)>>1;build(lson);build(rson);
}
void pushup(int rt) {tree[rt].cov=min(tree[ls].cov,tree[rs].cov);
}
void change(int rt,int val) {tree[rt].cov+=val;tree[rt].lazy+=val;
}
void pushdown(int rt) {change(ls,tree[rt].lazy);change(rs,tree[rt].lazy);tree[rt].lazy=0;
}
void update(int l,int r,int val,int rt) {if(tree[rt].l==l&&tree[rt].r+1==r) {change(rt,val);return ;}if(tree[rt].lazy) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid+1) update(l,r,val,ls);else if(l>=mid+1) update(l,r,val,rs);else update(l,mid+1,val,ls),update(mid+1,r,val,rs);pushup(rt);
}
int query(int l,int r,int rt) {if(tree[rt].l==l&&tree[rt].r+1==r) {if(tree[rt].cov) return v[r-1]-v[l-1];else if(tree[rt].l==tree[rt].r) return 0; }if(tree[rt].lazy) pushdown(rt);int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid+1) return query(l,r,ls);else if(l>=mid+1) return query(l,r,rs);else return query(l,mid+1,ls)+query(mid+1,r,rs);
}
signed main() {n=read();int cnt=0;for(int i=1;i<=n;i++) {int a=read(),b=read(),h=read();line[++cnt].l=a;line[cnt].r=b;line[cnt].y=0;line[cnt].cate=1;line[++cnt].l=a;line[cnt].r=b;line[cnt].y=h;line[cnt].cate=-1;v.push_back(b);v.push_back(a);}sort(line+1,line+2*n+1);sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int Size=v.size();build(1,Size,1);int ans=0;for(int i=1;i<=2*n-1;i++) {int x1=Get_id(line[i].l),x2=Get_id(line[i].r);update(x1,x2,line[i].cate,1);ans+=query(1,Size,1)*(line[i+1].y-line[i].y);}cout<<ans<<endl;return 0;
}
下面是具体的代码部分(不维护pushdownpushdownpushdown版):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{int l,r,cov,len;
}tree[maxn*4];
int n;vector<int>v;
int Get_id(int x) {return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
struct Line{int l,r,y,cate;bool operator < (const Line &rhs) const {return y<rhs.y;}
}line[maxn];
void build(int l,int r,int rt) {tree[rt].l=l;tree[rt].r=r;if(l==r) return ;int mid=(l+r)>>1;build(lson);build(rson);
}
void pushup(int rt) {if(tree[rt].cov) tree[rt].len=v[tree[rt].r]-v[tree[rt].l-1];else tree[rt].len=tree[ls].len+tree[rs].len;
}
void update(int l,int r,int val,int rt) {if(tree[rt].l==l&&tree[rt].r+1==r) {tree[rt].cov+=val;if(tree[rt].cov) tree[rt].len=v[r-1]-v[l-1];else pushup(rt);return ;}int mid=(tree[rt].l+tree[rt].r)>>1;if(r<=mid+1) update(l,r,val,ls);else if(l>=mid+1) update(l,r,val,rs);else update(l,mid+1,val,ls),update(mid+1,r,val,rs);pushup(rt);
}
signed main() {n=read();int cnt=0;for(int i=1;i<=n;i++) {int a=read(),b=read(),h=read();line[++cnt].l=a;line[cnt].r=b;line[cnt].y=0;line[cnt].cate=1;line[++cnt].l=a;line[cnt].r=b;line[cnt].y=h;line[cnt].cate=-1;v.push_back(b);v.push_back(a);}sort(line+1,line+2*n+1);sort(v.begin(),v.end());v.erase(unique(v.begin(),v.end()),v.end());int Size=v.size();build(1,Size,1);int ans=0;for(int i=1;i<=2*n-1;i++) {int x1=Get_id(line[i].l),x2=Get_id(line[i].r);update(x1,x2,line[i].cate,1);ans+=tree[1].len*(line[i+1].y-line[i].y);}cout<<ans<<endl;return 0;
}
相关文章:

刷题记录:牛客NC25078[USACO 2007 Ope S]City Horizon
传送门:牛客 题目描述: Farmer John has taken his cows on a trip to the city! As the sun sets, the cows gaze at the city horizon and observe the beautiful silhouettes formed by the rectangular buildings. The entire horizon is represented by a number line …...

【Java|golang】 1238. 循环码排列---格雷编码
给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,…,2^n-1) 的排列 p,并且满足: p[0] start p[i] 和 p[i1] 的二进制表示形式只有一位不同 p[0] 和 p[2^n -1] 的二进制表示形式也只有一位不同 示例 1: 输入:n 2, start …...

Python自动化测试框架封装和调用
封装与调用函数与参数化前言 面实现了参数的关联,那种只是记流水账的完成功能,不便于维护,也没什么可读性,接下来这篇可以把每一个动作写成一个函数,这样更方便了。参数化的思维只需记住一点:不要写死 登录…...
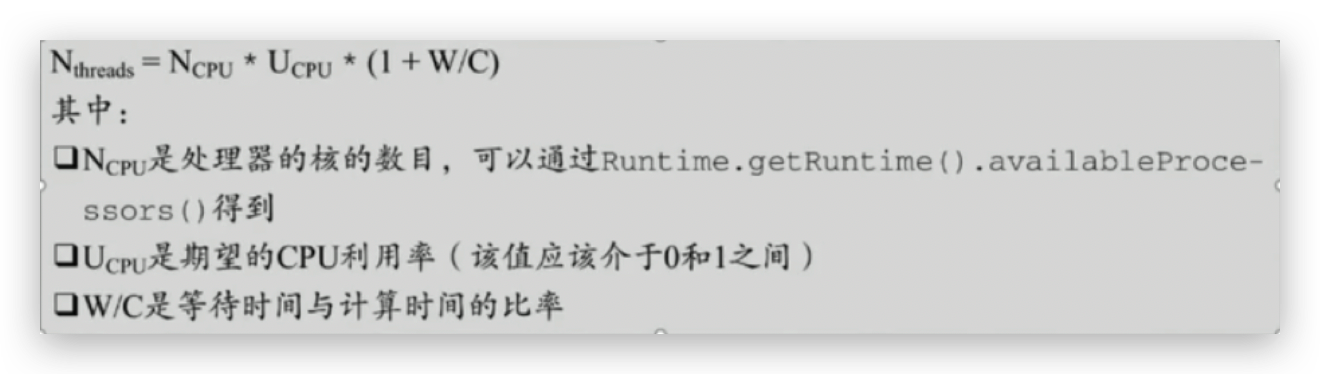
线程的执行
承接上文CPU原理简介程序的执行是由控制器发信号推动整个程序一步一步向前走,将数据存储在寄存器,从程序计数器中获取指令,比如先把3放到寄存器,再把5放到寄存器,再做一个加法,加法就是一个指令,…...

【视频】海康摄像头、NVR网络协议简介
1、软硬件整体架构 2、涉及的网络协议 3、协议简介 3.1 海康私有协议 设备发现SADP:进行设备的发现、激活、修改网络参数、忘记密码等; SDK:4200、系统平台的接入前端设备,协议不对外开放,但对外提供接口库; ISAPI:Intelligent Security API(智能安全API),基于HTTP传输…...

【Spring的事务传播行为有哪些呢?Spring事务的隔离级别?讲下嵌套事务?】
如果你想寻求一份与后端相关的开发工作,那么关于Spring事务相关的面试题你就不能说不会并且不能不知道? 人生如棋,我愿为卒,行动虽慢,可谁曾见我后退一步? 一.Spring中声明事务的方式 1.1 编程式事务 编程…...

其实一点不难学会这三步一定让你学会制作一个『3D建模』大屏
上次已经教过大家怎样制作一个简单的2D数据可视化大屏~那有一些朋友们就会说那些炫酷的3D可视化大屏是怎样制作的呢?这不就来了,今天就教大家怎样用山海鲸可视化软件制作一个带3D建模的可视化大屏,并且最重要的是无需会特别复杂的3D建模知识。…...
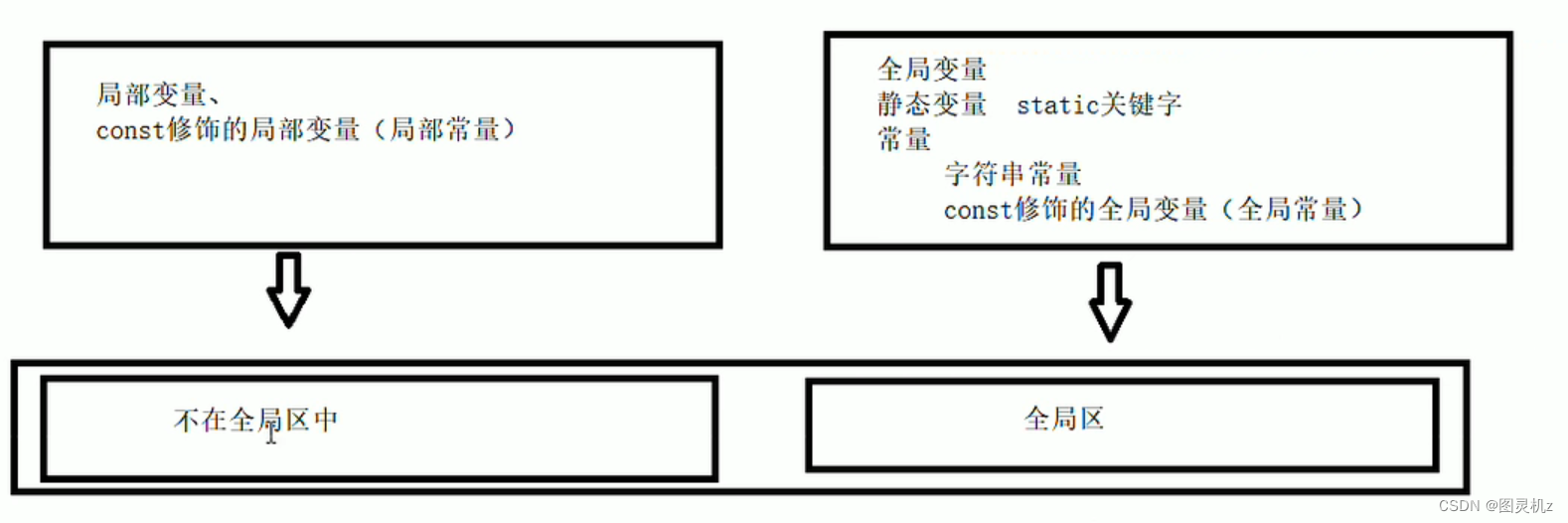
【C++】C++的内存模型之四大分区
程序的内存模型 C程序在执行时,将内存大方向划分为4个区域 代码区:存放函数体的二进制代码,由操作系统进行管理的全局区:存放全局变量和静态变量以及常量栈区:由编译器自动分配释放,存放函数的参数值&…...

Vue跨级通信(重点)
当不使用Vuex的前提下,子孙传递就得使用另外一种办法:provide 和 inject 总结:provide / inject 类似于消息的订阅和发布。- inject接收数据。- provide提供或发送数据,(1)provide(name…...

支付系统中的设计模式07:责任链模式
最近公司业务的发展果然如老板当初所画(预)饼(言)的那样红(恍)红(恍)火(惚)火(惚),蒸蒸日上,每天的流水都在不断攀升到新的高度,有不少人都从公司开发的电商平台挣到了钱。 不过问题也接着来了——运营部门经过老板的同意,也学着产品经理提出了下面几项非常合理…...

期末综合考试
一、概率论1、全概率公式、贝叶斯公式应用2、期望、方差、协方差的定义以及性质证明(1) 期望(2) 方差(3) 协方差二、数理统计1、参数估计(1) 矩估计(2) 最大似然估计(3) 综合例题一、概率论 1、全概率公式、贝叶斯公式应用 记住标黄的两段,上考场直接套数据&#x…...
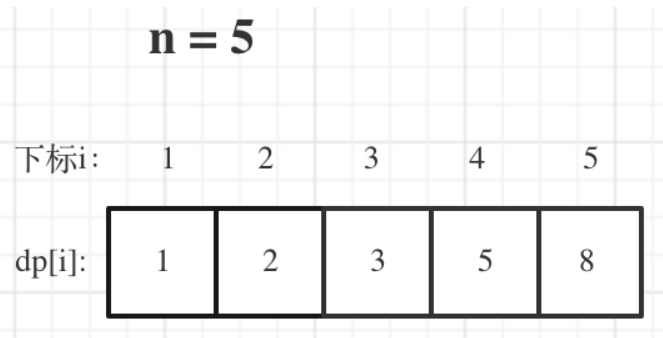
数据结构与算法之爬楼梯动态规划
一.题目(爬楼梯)假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数。示例 1:输入: 2输出: 2解释: 有两种方法可以爬…...
CleanMyMac4.12最新Mac电脑系统垃圾清理神器
CleanMyMac是Mac一款神器,特别是清理已卸载软件残留垃圾文件信息库比较全面。 clearmymac以极其快速和时尚的方式为您提供及时的建议,组织,更新和保护您的Mac。完全支持macOS 11(Big Sur)操作系统;它以其简…...

数据治理如何做?火山引擎 DataLeap 帮助这款产品 3 个月降低计算成本 20%
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 本文讲述字节跳动一款 App 产品的数据治理故事。该产品随着用户体量和数据体量不断增长,数仓的任务量、数据量也不断攀升,运维难、成本贵、稳…...
求职3个月,简历大多都石沉大海,一听是手工测试都纷纷摇头....太难了
距离被上家公司裁员已经过去了3个月了,3个月的求职经历真的让我痛不欲生,我也从中理解感叹到了很多,想写出来,告诫跟我一样的经历的人。 我今年26岁,大学是一所普通的大专,学的是机电专业,如何…...

Visual Studio快捷键汇总
常用快捷键CtrlEC 注释代码CtrlEU 取消注释代码CtrlED 格式化全部代码CtrlShiftA 新建类CtrlRG 删除无效UsingCtrlH 批量替换CtrlG 跳转到指定行CtrlEE 在交互窗口中运行选中代码(很实用)AltEnter 快速引用shiftF9 监控(代码运行时)shiftF6 生成(当前类库)F6 生成(整个解决方案…...

ctf pwn基础-2
今天学了一个保护的绕过,这里讲一讲,这个好像是使用的是格式化字符串漏洞。 目录 基础 实例讲解 基础 首先我们要知道什么是canary保护,就是在入栈EBP以后加一个Canary 我可能讲的不是很好,大家可以看看这些 文章 用通俗一点将就…...

从一个SQL打印全年日历漫谈数据仓库中时间操作场景的重点写法
文章目录前言一、我如何快速确定今年是否是闰年的😣二、 我如何从DATE类型数据获取年、月(月初&月末)、周、日、时、分、秒信息🤯三、我如何快速查到本月月初第一周的周一和本月最后一周周一是在几号😑四、我如何快速确定每个季度的开始和…...

Java跳槽涨薪之路-想学Java的赶紧上车了
前言Java 是近 10 年来计算机软件发展过程中的传奇,在很多开发者心中的地位可谓“爱不释手”,与其他一些计算机语言随着时间的流逝影响也逐渐减弱不同,Java 随着时间的推移反而变得更加强大。按应用范围,Java 可分为 3 个体系&…...

MyBatis解析全局配置文件
目录 MyBatis介绍 传统JDBC和Mybatis相比的弊病 传统JDBC的问题如下 mybatis对传统的JDBC的解决方案 Mybaits整体体系图 使用大致过程 MyBatis 源码编译 源码解析 配置文件解析 读取配置文件 返回SqlSessionFactory 配置文件内容 解析的核心方法 解析出来的对象 …...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

Yii2项目自动向GitLab上报Bug
Yii2 项目自动上报Bug 原理 yii2在程序报错时, 会执行指定action, 通过重写ErrorAction, 实现Bug自动提交至GitLab的issue 步骤 配置SiteController中的actions方法 public function actions(){return [error > [class > app\helpers\web\ErrorAction,],];}重写Error…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...
代理服务器-LVS的3种模式与调度算法
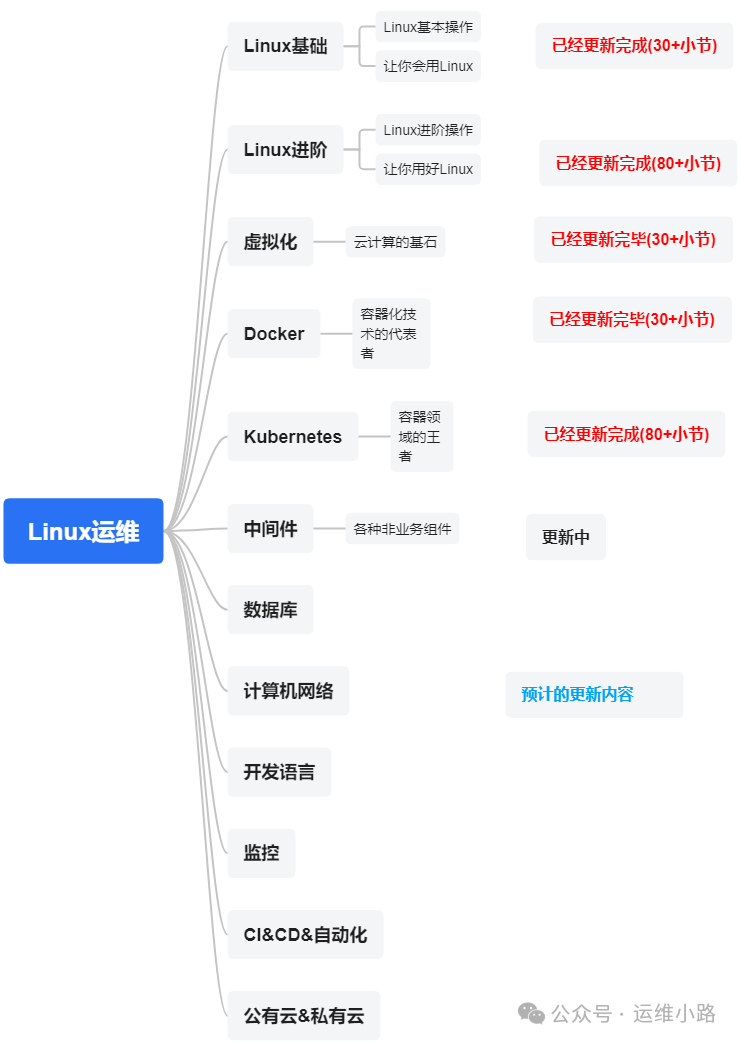
作者介绍:简历上没有一个精通的运维工程师。请点击上方的蓝色《运维小路》关注我,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 我们上一章介绍了Web服务器,其中以Nginx为主,本章我们来讲解几个代理软件:…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...
