数据结构与算法之爬楼梯动态规划
一.题目(爬楼梯)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。
你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
思路
本题大家如果没有接触过的话,会感觉比较难,多举几个例子,就可以发现其规律。
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
1)确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
2)确定递推公式
如何可以推出dp[i]呢?
从dp[i]的定义可以看出,dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
在推导dp[i]的时候,一定要时刻想着dp[i]的定义,否则容易跑偏。
这体现出确定dp数组以及下标的含义的重要性!
3)dp数组如何初始化
在回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]中方法。
那么i为0,dp[i]应该是多少呢,这个可以有很多解释,但基本都是直接奔着答案去解释的。
例如强行安慰自己爬到第0层,也有一种方法,什么都不做也就是一种方法即:dp[0] = 1,相当于直接站在楼顶。但总有点牵强的成分。
那还这么理解呢:我就认为跑到第0层,方法就是0啊,一步只能走一个台阶或者两个台阶,然而楼层是0,直接站楼顶上了,就是不用方法,dp[0]就应该是0.
其实这么争论下去没有意义,大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过,然后就往结果上靠去解释dp[0] = 1。
从dp数组定义的角度上来说,dp[0] = 0 也能说得通。
需要注意的是:题目中说了n是一个正整数,题目根本就没说n有为0的情况。
所以本题其实就不应该讨论dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,这个初始化大家应该都没有争议的。
所以原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4)确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的。
5)举例推导dp数组
举例当n为5的时候,dp table(dp数组)应该是这样的:
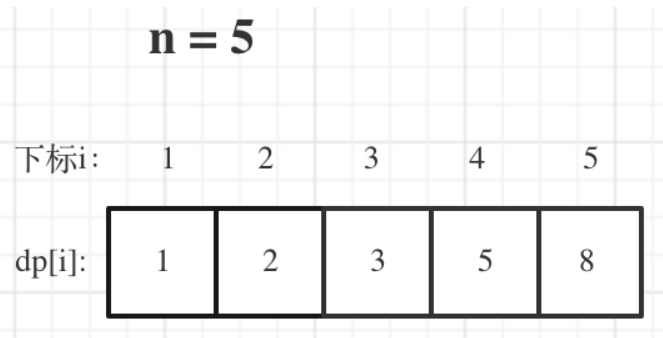
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
此时大家应该发现了,这不就是斐波那契数列么!
唯一的区别是,没有讨论dp[0]应该是什么,因为dp[0]在本题没有意义!
以上五部分析完之后,C++代码如下:
// 版本一
class Solution {
public:int climbStairs(int n) {if (n <= 1) return n; // 因为下面直接对dp[2]操作了,防止空指针vector<int> dp(n + 1);dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) { // 注意i是从3开始的dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};时间复杂度:$O(n)$
空间复杂度:$O(n)$
当然依然也可以,优化一下空间复杂度,代码如下:
// 版本二
class Solution {
public:int climbStairs(int n) {if (n <= 1) return n;int dp[3];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};时间复杂度:$O(n)$
空间复杂度:$O(1)$
后面将讲解的很多动规的题目其实都是当前状态依赖前两个,或者前三个状态,都可以做空间上的优化。
相关文章:

数据结构与算法之爬楼梯动态规划
一.题目(爬楼梯)假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数。示例 1:输入: 2输出: 2解释: 有两种方法可以爬…...
CleanMyMac4.12最新Mac电脑系统垃圾清理神器
CleanMyMac是Mac一款神器,特别是清理已卸载软件残留垃圾文件信息库比较全面。 clearmymac以极其快速和时尚的方式为您提供及时的建议,组织,更新和保护您的Mac。完全支持macOS 11(Big Sur)操作系统;它以其简…...

数据治理如何做?火山引擎 DataLeap 帮助这款产品 3 个月降低计算成本 20%
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 本文讲述字节跳动一款 App 产品的数据治理故事。该产品随着用户体量和数据体量不断增长,数仓的任务量、数据量也不断攀升,运维难、成本贵、稳…...
求职3个月,简历大多都石沉大海,一听是手工测试都纷纷摇头....太难了
距离被上家公司裁员已经过去了3个月了,3个月的求职经历真的让我痛不欲生,我也从中理解感叹到了很多,想写出来,告诫跟我一样的经历的人。 我今年26岁,大学是一所普通的大专,学的是机电专业,如何…...

Visual Studio快捷键汇总
常用快捷键CtrlEC 注释代码CtrlEU 取消注释代码CtrlED 格式化全部代码CtrlShiftA 新建类CtrlRG 删除无效UsingCtrlH 批量替换CtrlG 跳转到指定行CtrlEE 在交互窗口中运行选中代码(很实用)AltEnter 快速引用shiftF9 监控(代码运行时)shiftF6 生成(当前类库)F6 生成(整个解决方案…...

ctf pwn基础-2
今天学了一个保护的绕过,这里讲一讲,这个好像是使用的是格式化字符串漏洞。 目录 基础 实例讲解 基础 首先我们要知道什么是canary保护,就是在入栈EBP以后加一个Canary 我可能讲的不是很好,大家可以看看这些 文章 用通俗一点将就…...

从一个SQL打印全年日历漫谈数据仓库中时间操作场景的重点写法
文章目录前言一、我如何快速确定今年是否是闰年的😣二、 我如何从DATE类型数据获取年、月(月初&月末)、周、日、时、分、秒信息🤯三、我如何快速查到本月月初第一周的周一和本月最后一周周一是在几号😑四、我如何快速确定每个季度的开始和…...

Java跳槽涨薪之路-想学Java的赶紧上车了
前言Java 是近 10 年来计算机软件发展过程中的传奇,在很多开发者心中的地位可谓“爱不释手”,与其他一些计算机语言随着时间的流逝影响也逐渐减弱不同,Java 随着时间的推移反而变得更加强大。按应用范围,Java 可分为 3 个体系&…...

MyBatis解析全局配置文件
目录 MyBatis介绍 传统JDBC和Mybatis相比的弊病 传统JDBC的问题如下 mybatis对传统的JDBC的解决方案 Mybaits整体体系图 使用大致过程 MyBatis 源码编译 源码解析 配置文件解析 读取配置文件 返回SqlSessionFactory 配置文件内容 解析的核心方法 解析出来的对象 …...

37-Golang中的封装
封装介绍 封装就是把抽象出的字段和对字段的操作封装在一起,数据被保护在内部,程序的其他包只有通过被授权的操作(方法),才能对字段进行操作 封装的理解和好处 1.隐藏实现细节 2.可以对数据进行验证,保证安全合理 如何体现封…...
Python Pytorch开发环境搭建(Windows和Ubuntu)
Python Pytorch开发环境搭建(Windows和Ubuntu) 目录 Pytorch开发环境搭建 1. 安装cuda cudnn (1)Windows安装方法 (2)Ubuntu18.04安装方法 2. 安装Python(推荐使用Anaconda) (1)Windows安装方法 (2)Ubuntu18.04安装方法 3. Pytorch安装 4. 安装…...
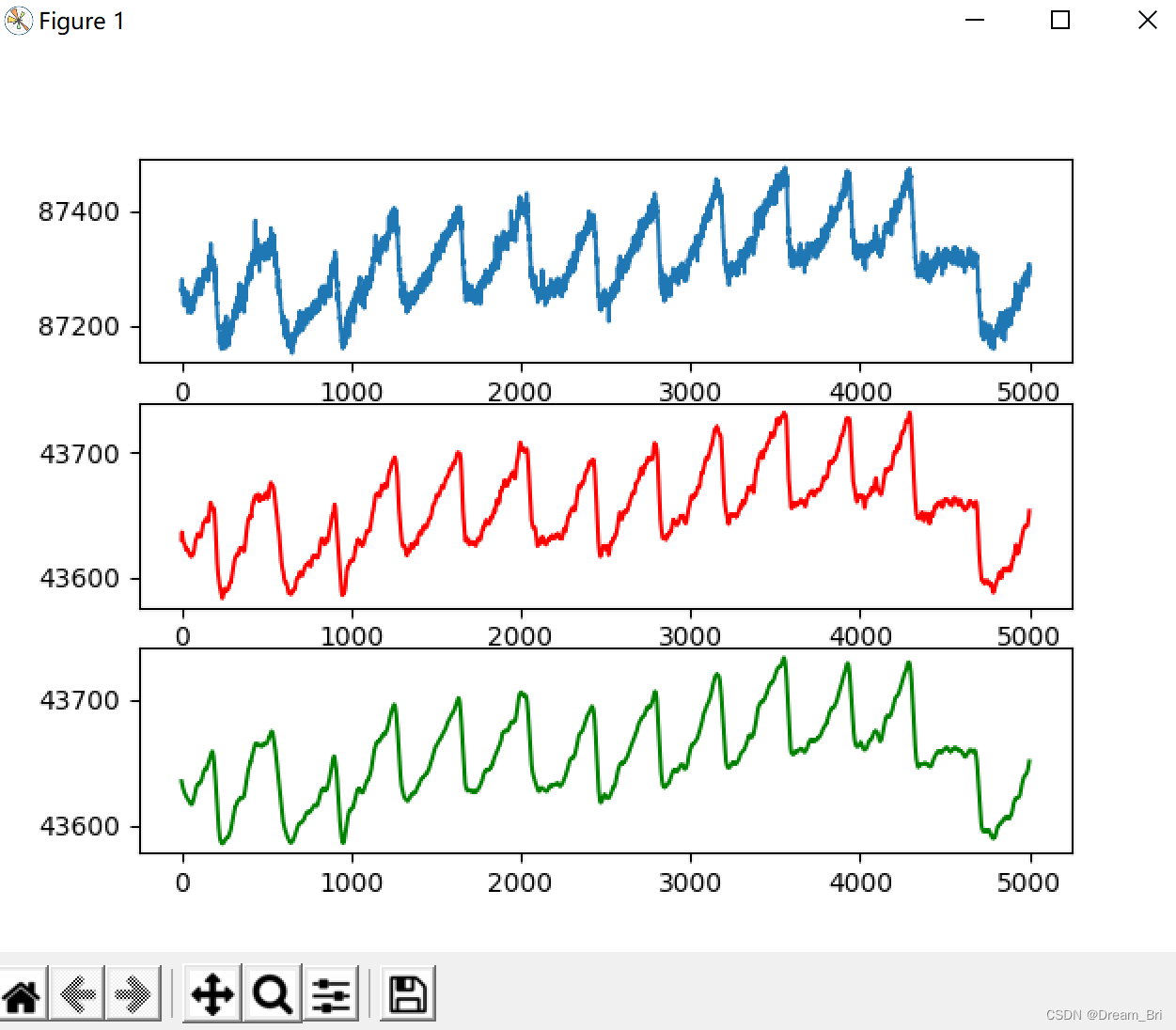
多种方法进行去基线处理
目录detrend函数去除基线多项式拟合原函数BEADS 基线处理小波算法经验模态分解(EMD)参考detrend函数去除基线 detrend函数只能用于去除线性趋势,对于非线性的无能为力。 函数表达式:y scipy.signal.detrend(x): 从信号中删除线…...
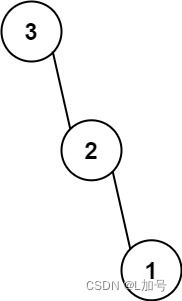
二叉树——最大二叉树
最大二叉树 链接 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums…...
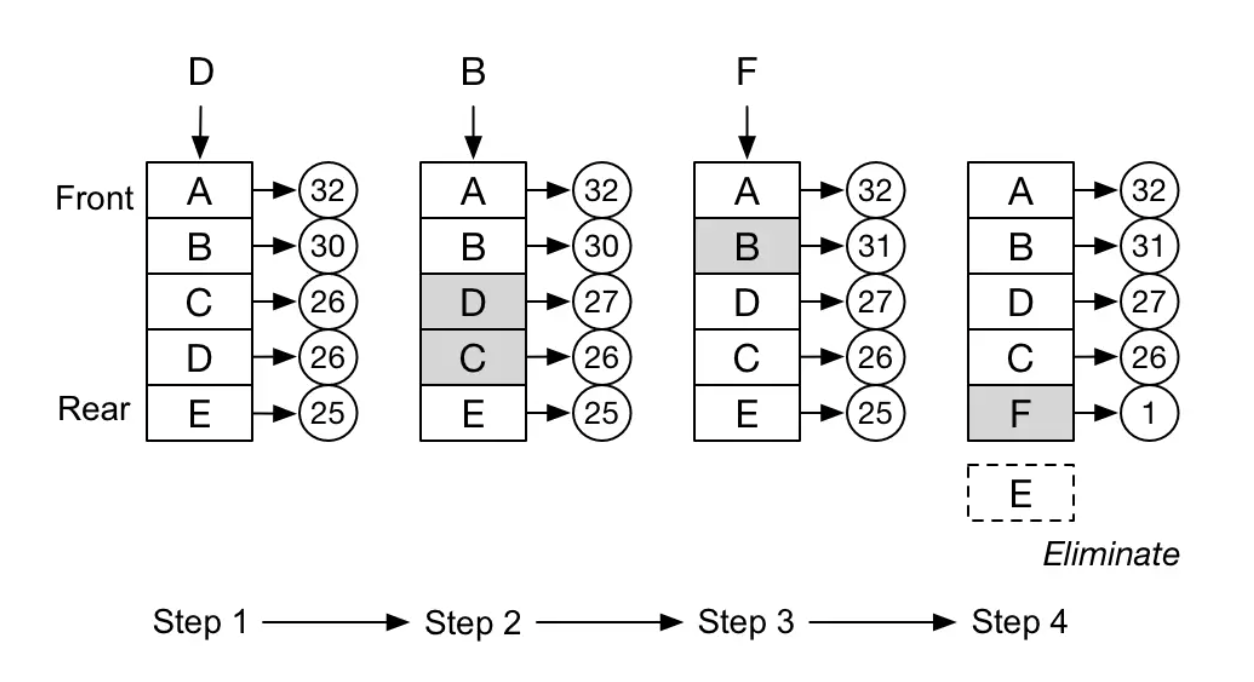
【Redis】Redis 的过期策略以及内存淘汰机制详解
Redis 的过期策略以及内存淘汰机制详解1. Redis 的过期策略1.1 如何设置 key 的过期时间?1.2 key 设置且到了过期时间后,该 key 保存的数据还占据内存么?1.3 Redis 如何删除过期的数据1.3.1 定期删除1.3.2 惰性删除2. Redis 的内存淘汰机制2.…...
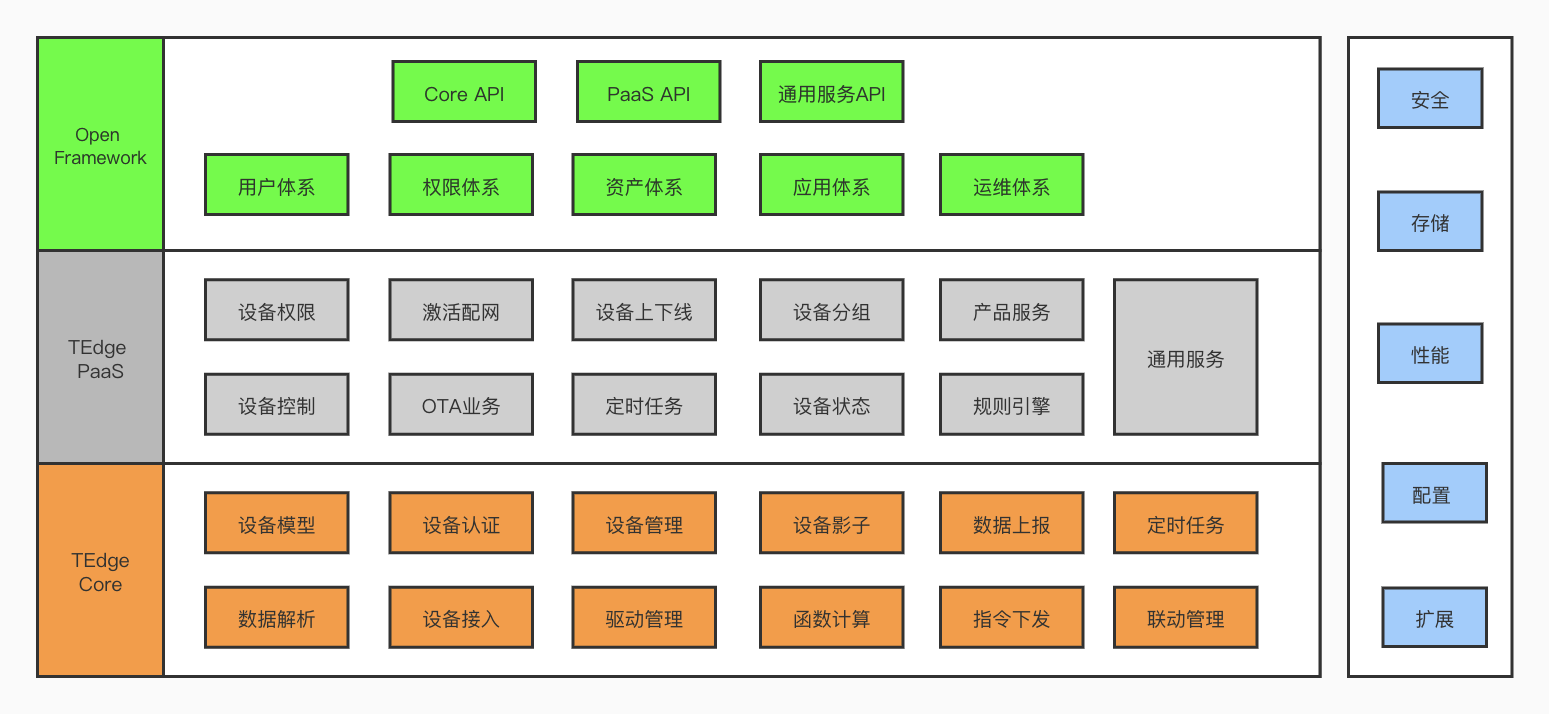
边缘云是什么?
涂鸦边缘云服务 旨在解决物联网边缘位置的连接需求和提高设备自主管理能力。并与涂鸦 IoT 云服务和 IoT 终端形成云边端三位一体的端到端产品架构。使用涂鸦边缘云,能极大降低设备响应延时、降低网络带宽压力、提高算力分发能力,并构建以下技术优势&…...

Java常用数据结构
Java常用数据结构 Java中有几种常用的数据结构,主要分为Collection和map两个主要接口(接口只提供方法,并不提供实现),而程序中最终使用的数据结构是继承自这些接口的数据结构类。 一、几个常用类的区别 1.…...
【Java基础 下】 026 -- 集合进阶(不可变集合、Stream流、方法引用)
目录 一、不可变集合 1、创建不可变集合的应用场景 2、创建不可变集合的书写格式 ①、不可变的List集合 ②、不可变的Set集合 ③、不可变的Map集合 3、小结 二、Stream流 1、体验Stream流的作用 2、Stream流的思想 3、Stream流的使用步骤 ①、单列集合获取Stream流 ②、双列集合…...

SAP 跨工厂或特定工厂的物料状态设置
在物料主数据的Basic data 1 View和MRP1 View可分别设置“跨工厂物料状态(X-plant matl status)”和“特定工厂的物料状态(Plant-sp.matl status)”。 通过对物料状态的设置,可实现对物料使用范围的限制。 例:在采购中不可用;在库存管理中不…...

jupyter的安装步骤
1.安装python文件 首先去官网python去下载python的安装包,点击donwload,选择合适的系统。这里我是windown系统,点击进去,如图找到有installer的去下载。不建议下载最新版本的,会有兼容问题。 2.安装python 点击第二个选项是自己配…...

Optional使用详解
Optional使用详解 文章目录Optional使用详解1.构造函数2.Optional.of(T value)作用使用源码(只想知道怎么用的可以略过)Optional.ofNullable(T value)作用使用源码.orElse(T other)作用使用源码.orElseGet(Supplier<? extends T> other)作用使用源…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
