代码随想录笔记--动态规划篇
1--动态规划理论基础
动态规划经典问题:① 背包问题;② 打家劫舍;③ 股票问题; ④ 子序列问题;
动态规划五部曲:
① 确定 dp 数组及其下标的含义;
② 确定递推公式;
③ 确定 dp 数组的初始化;
④ 确定遍历顺序,一般为从左到右;
⑤ 打印 dp 数组,一般用于检查;
2--斐波那契数

主要思路:
经典动态规划,dp[i] 表示第 i 个数的斐波那契数;递推公式为:dp[i] = dp[i-1] + dp[i - 2];初始化dp[0] = 1,dp[1] = 1;遍历顺序从左到右;
#include <iostream>
#include <vector>class Solution {
public:int fib(int n) {if(n <= 1) return n;std::vector<int> dp(n+1, 0);dp[0] = 0; dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};int main(int argc, char argv[]){int test = 2;Solution S1;int res = S1.fib(test);std::cout << res << std::endl;return 0;
}
3--爬楼梯
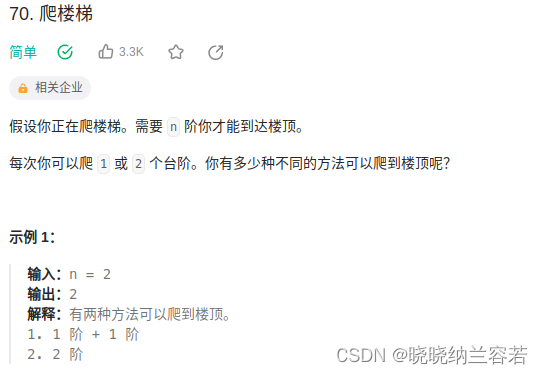
主要思路:
经典动态规划,dp[i] 表示到达第 i 阶楼梯的方法数;递推公式为 dp[i] = dp[i - 1] + dp[i - 2];初始化dp[1] = 1, dp[2] = 2;遍历顺序从左到右;
#include <iostream>
#include <vector>class Solution {
public:int climbStairs(int n) {if(n <= 2) return n; std::vector<int> dp(n+1, 0);dp[1] = 1, dp[2] = 2;for(int i = 3; i <= n; i++){dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
};int main(int argc, char argv[]){int n = 2;Solution S1;int res = S1.climbStairs(n); std::cout << res << std::endl;return 0;
}
4--使用最小花费爬楼梯

主要思路:
dp[i] 表示到达第 i 阶楼梯需要的最小花费;初始化 dp[0] = 0, dp[1] = 0,因为可以从 0 和 1 出发,因此不需要花费;递推公式为 dp[i] = std::min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);默认从左到右遍历;
#include <iostream>
#include <vector>class Solution {
public:int minCostClimbingStairs(std::vector<int>& cost) {std::vector<int> dp(cost.size()+1, 0); // 到达第i阶的最小花费dp[0] = 0;dp[1] = 0;for(int i = 2; i <= cost.size(); i++){dp[i] = std::min(cost[i-2]+dp[i-2], cost[i-1]+dp[i-1]);}return dp[cost.size()];}
};int main(int argc, char argv[]){// cost = [1,100,1,1,1,100,1,1,100,1]std::vector<int> cost = {1, 100, 1, 1, 1, 100, 1, 1, 100, 1};Solution S1;int res = S1.minCostClimbingStairs(cost);std::cout << res << std::endl;return 0;
}
5--不同路径

主要思路:
dp[i][j] 表示到达 (i, j) 位置的路径数,初始化两个边界 dp[i][0] = 1,dp[0][j] = 1;状态转移方程为:dp[i][j] = dp[i-1][j] + dp[i][j-1];遍历顺序为从上到下,从左到右;
#include <iostream>
#include <vector>class Solution {
public:int uniquePaths(int m, int n) {std::vector<std::vector<int>> dp(m, std::vector<int>(n, 0));// 初始化for(int i = 0; i < m; i++) dp[i][0] = 1;for(int j = 0; j < n; j++) dp[0][j] = 1;// 遍历for(int r = 1; r < m; r++){for(int c = 1; c < n; c++){dp[r][c] = dp[r-1][c] + dp[r][c-1];}}return dp[m-1][n-1];}
};int main(int argc, char argv[]){// m = 3, n = 7int m = 3, n = 7;Solution S1;int res = S1.uniquePaths(m, n);std::cout << res << std::endl;return 0;
}
6--不同路径II

主要思路:
与上题类似,dp[i][j] 表示到达 (i, j) 位置的路径数,初始化两个边界 dp[i][0] = 1,dp[0][j] = 1(确保边界没有障碍物,有障碍物初始化为0);状态转移方程为:(i, j)不是障碍物则 dp[i][j] = dp[i-1][j] + dp[i][j-1],(i, j)为障碍物则dp[i][j] = 0;遍历顺序为从上到下,从左到右;
#include <iostream>
#include <vector>class Solution {
public:int uniquePathsWithObstacles(std::vector<std::vector<int>>& obstacleGrid) {int m = obstacleGrid.size(), n = obstacleGrid[0].size();if(obstacleGrid[m-1][n-1] == 1) return 0;std::vector<std::vector<int>> dp(m, std::vector<int>(n, 0));// 初始化for(int i = 0; i < m && obstacleGrid[i][0] != 1; i++) dp[i][0] = 1;for(int j = 0; j < n && obstacleGrid[0][j] != 1; j++) dp[0][j] = 1;// 遍历for(int r = 1; r < m; r++){for(int c = 1; c < n; c++){if(obstacleGrid[r][c] == 1) dp[r][c] = 0; // 障碍else dp[r][c] = dp[r-1][c] + dp[r][c-1];}}return dp[m-1][n-1];}
};int main(int argc, char argv[]){// obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]std::vector<std::vector<int>> test = {{0, 0, 0}, {0, 1, 0}, {0, 0, 0}};Solution S1;int res = S1.uniquePathsWithObstacles(test);std::cout << res << std::endl;return 0;
}
7--整数拆分

主要思路:
dp[i] 表示整数 i 拆分后的最大乘积;初始化dp[0] = 0, dp[1] = 0, dp[2] = 1; 状态转移方程为:dp[i] = max(dp[i], max(j*(i-j), j * dp[i-j]));
#include <iostream>
#include <vector>class Solution {
public:int integerBreak(int n) {std::vector<int> dp(n+1, 0);// 初始化dp[0] = 0, dp[1] = 0, dp[2] = 1;// 遍历for(int i = 3; i <= n; i++){for(int j = 0; j <= i/2; j++){dp[i] = std::max(dp[i], std::max(j*(i-j), j * dp[i-j]));}}return dp[n];}
};int main(int argc, char argv[]){// n = 10int test = 10;Solution S1;int res = S1.integerBreak(test);std::cout << res << std::endl;return 0;
}
8--不同的二叉搜索树
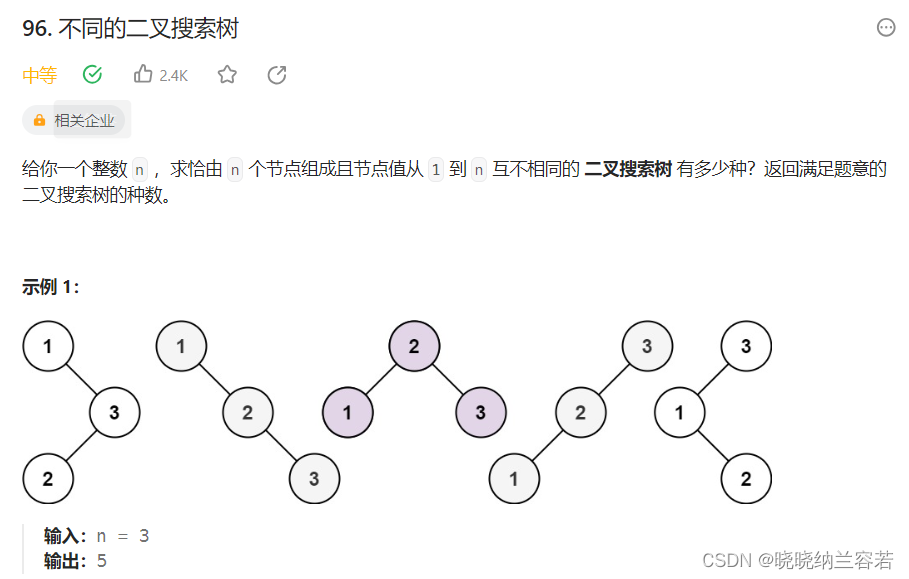
主要思路:
dp[i] 表示由 i 个数字构成的不同二叉搜索树的数目;
初始化:dp[0] = 1;
状态转移方程:dp[i] += dp[j-1] * dp[i-j],0 <= j <= i;其中 dp[j-1] 来构成 j 的左子树,dp[i-j] 来构成 j 的右子树;
遍历顺序:两个 for 循环,第 1 个 for 循环遍历 1 - n,第二个 for 循环遍历 1 - i;
#include <iostream>
#include <vector>class Solution {
public:int numTrees(int n) {std::vector<int> dp(n+1, 0);// 初始化dp[0] = 1;// 遍历for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};int main(int argc, char *argv[]) {// n = 3int test = 3;Solution S1;int res = S1.numTrees(test);std::cout << res << std::endl;return 0;
}9--
相关文章:

代码随想录笔记--动态规划篇
1--动态规划理论基础 动态规划经典问题:① 背包问题;② 打家劫舍;③ 股票问题; ④ 子序列问题; 动态规划五部曲: ① 确定 dp 数组及其下标的含义; ② 确定递推公式; ③ 确定 dp 数组…...

vue之vuex
Vuex 是 Vue.js 的一个状态管理模式和库,为应用中的所有组件提供了一个集中式的存储管理,并提供了一种强大的方式来管理应用的状态。Vuex 包含以下核心概念: State:定义了应用的状态,类似于组件中的 data。 Getters&a…...
)
ISO 26262 系列学习笔记 ———— ASIL定义(Automotive Safety Integration Level)
文章目录 介绍严重度(Severity)暴露概率(Probability of Exposure)可控性(Controllability) 介绍 如果没有另行说明,则应满足ASIL A、B、C和D各分条款的要求或建议。这些要求和建议参考了安全目…...

代码随想录 第8章 二叉树
1、理论知识 (1)、满二叉树 如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。 (2)、完全二叉树 除了底层节点可能没有填满,其余每层的节点…...
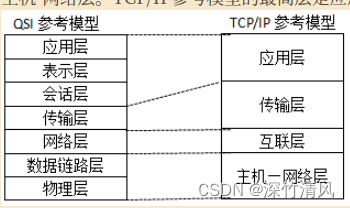
计算机网络工程师多选题系列——计算机网络
2 计算机网络 2.1 网络技术基础 题型1 TCP/IP与ISO模型的问题 TCP/IP由IETF制定,ISO由OSI制定; TCP/IP分为四层,分别是主机-网络层、互联网络层、传输层和应用层;OSI分为七层,分别是物理层、数据链路层、网络层(实…...
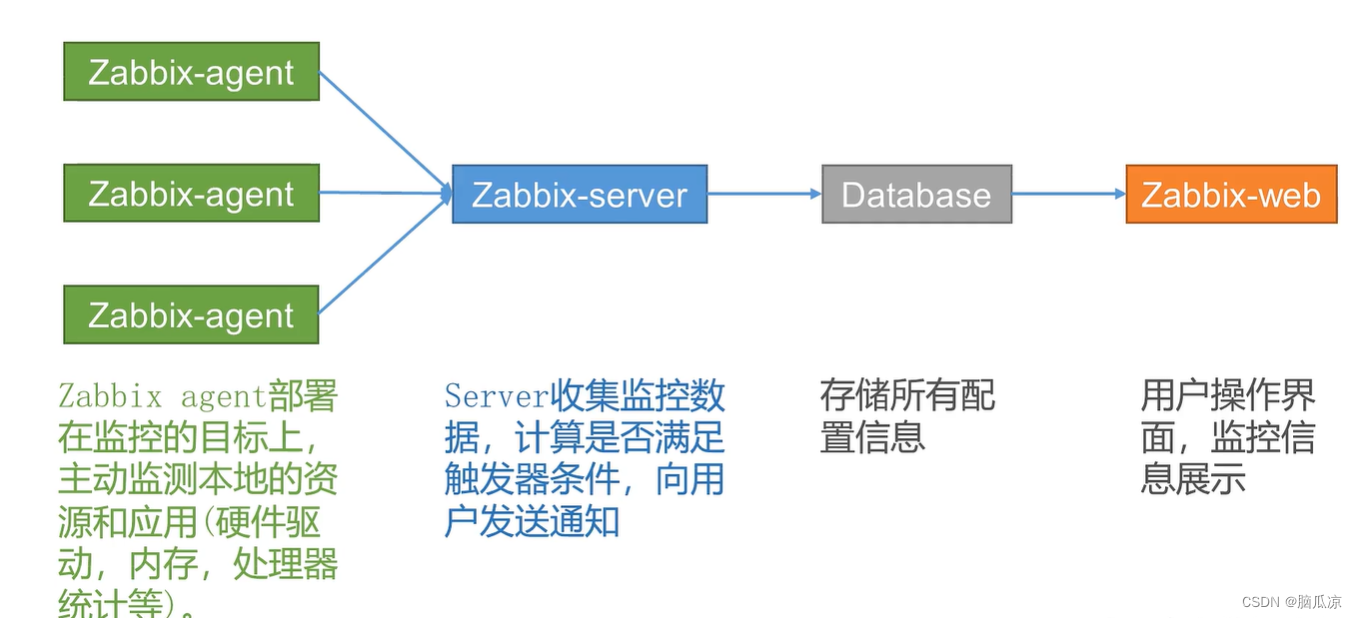
Zabbix5.0_介绍_组成架构_以及和prometheus的对比_大数据环境下的监控_网络_软件_设备监控_Zabbix工作笔记001
z 这里Zabbix可以实现采集 存储 展示 报警 但是 zabbix自带的,展示 和报警 没那么好看,我们可以用 grafana进行展示,然后我们用一个叫睿象云的来做告警展示, 会更丰富一点. 可以看到 看一下zabbix的介绍. 对zabbix的介绍,这个zabbix比较适合对服务器进行监控 这个是zabbix的…...
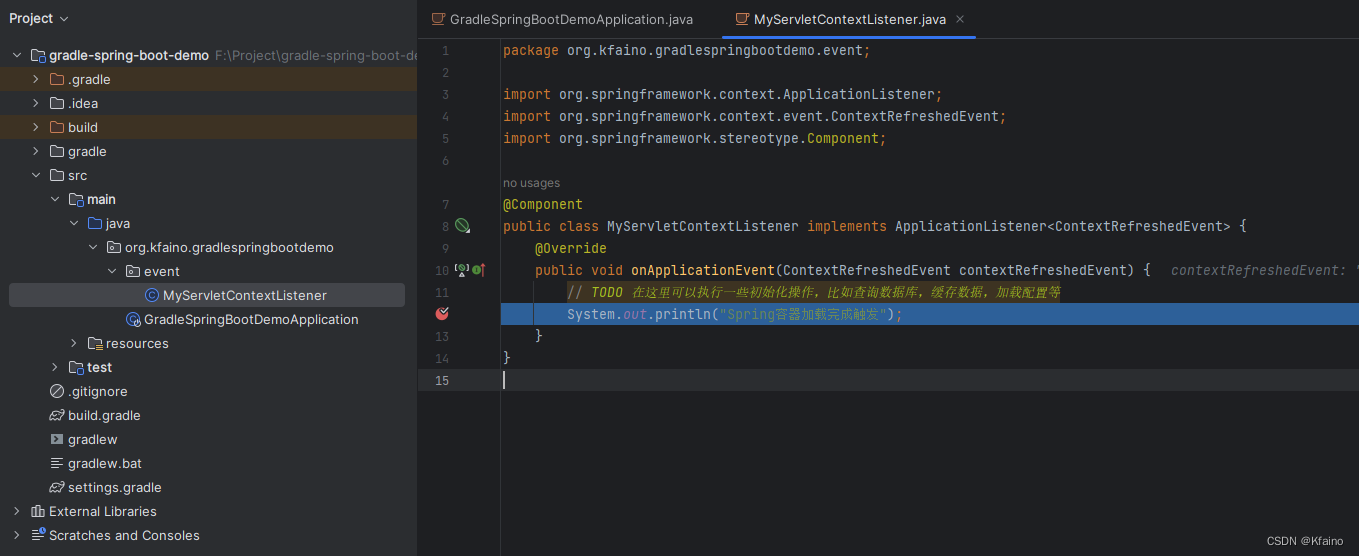
Spring | 事件监听器应用与最佳实践
引言 在复杂的软件开发环境中,组件之间的通信和信息交流显得尤为重要。Spring框架,作为Java世界中最受欢迎的开发框架之一,提供了一种强大的事件监听器模型,使得组件间的通信变得更加灵活和解耦。本文主要探讨Spring事件监听器的…...

正点原子lwIP学习笔记——NETCONN接口简介
1. NETCONN接口简介 NETCONN API 使用了操作系统的 IPC 机制, 对网络连接进行了抽象,使用同一的接口完成UDP和TCP连接。 NETCONN API接口是在RAW接口基础上延申出来的一套API接口 首先会调用netconn_new创建一个pcb控制块,其实际是一个宏定…...
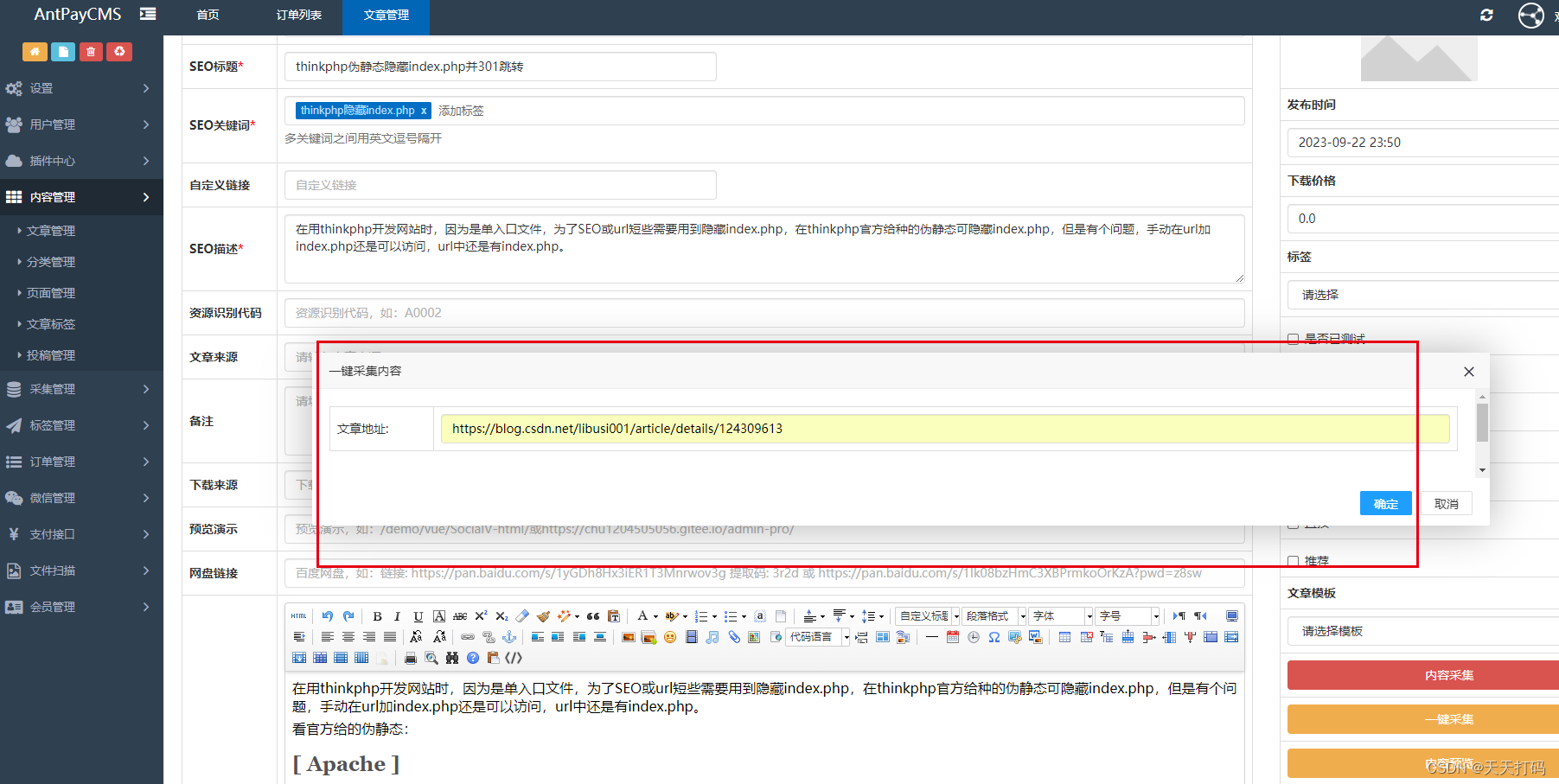
PHP自动识别采集何意网址文章正文内容
在做PHP采集内容时,用过querylist采集组件,但是这个插件采集页面内容时,都必须要写个采集选择器。这样比较麻烦,每个文章页面都必须指定一条采集规则 。就开始着手找一个插件可以能自动识别任意文章url正文内容并采集的࿰…...

区块链实验室(27) - 区块链+物联网应用案例
分享最新的区块链物联网应用案例:HPCLS-BC...
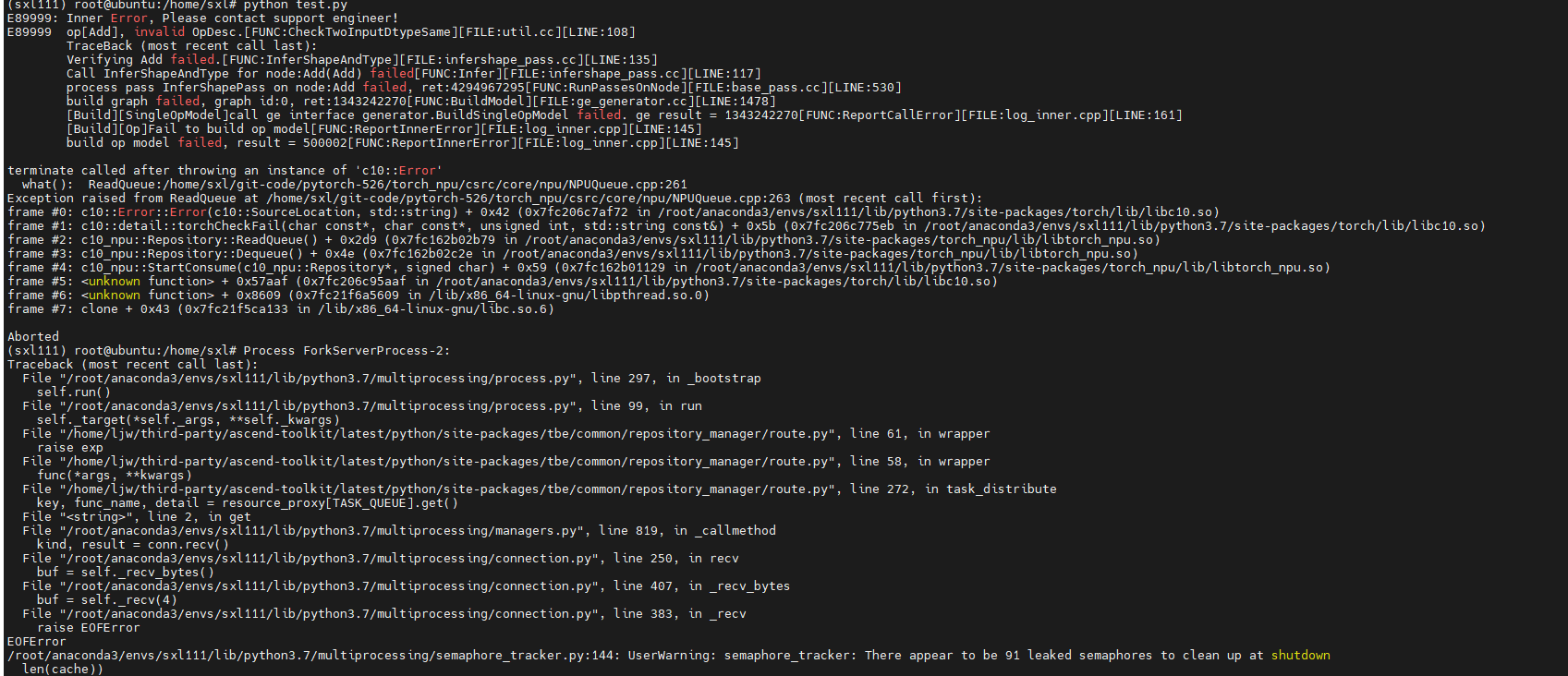
NPU上PyTorch模型训练问题案例
在昇腾AI处理器上训练PyTorch框架模型时,可能由于环境变量设置问题、训练脚本代码问题,导致打印出的堆栈报错与实际错误并不一致、脚本运行异常等问题,那么本期就分享几个关于PyTorch模型训练问题的典型案例,并给出原因分析及解决…...

出现 conda虚拟环境默认放在C盘 解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 方法一3.2 方法二1. 问题所示 通过conda配置虚拟环境的时候,由于安装在D盘下,但是配置的环境默认都给我放C盘 通过如下命令:conda env list,最后查看该环境的确在C盘下 2. 原理分析 究其根本原因,这是因为默认路径没有足够的…...

Ubuntu Postgresql开机自启动服务
1. 建立service文件 sudo vim /etc/systemd/system/postgresql.service2. postgresql service文件 [Unit] DescriptionPostgreSQL 14 database server Documentationman:postgres(1) Documentationhttp://www.postgresql.org/docs/14/static/ Afternetwork.target[Service] T…...

COTS即Commercial Off-The-Shelf 翻译为“商用现成品或技术”或者“商用货架产品”
COTS 使用“不再做修理或改进”的模式出售的商务产品 COTS即Commercial Off-The-Shelf 翻译为“商用现成品或技术”或者“商用货架产品”,指可以采购到的具有开放式标准定义的接口的软件或硬件产品,可以节省成本和时间。 中文名 商用现成品或技术 外文…...
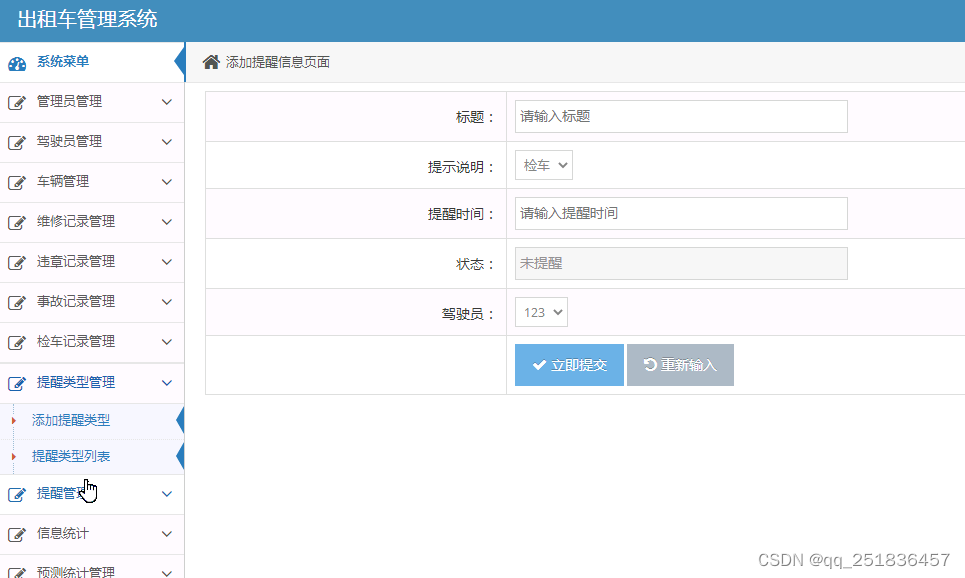
idea开发Springboot出租车管理系统VS开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 springboot 出租车管理系统是一套完善的完整信息系统,结合springboot框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用springboot框架(MVC模式开发), 系统具有完整的源代码和数据…...

Linux nohup
nohup 命令用于在 Linux 中将命令或程序在后台运行,并且在终端关闭后仍然保持运行。 nohup命令 描述 nohup 命令用于将命令或程序以不受终端挂断影响的方式在后台运行。 语法 nohup command [arguments] &参数 command:要在后台运行的命令或程…...
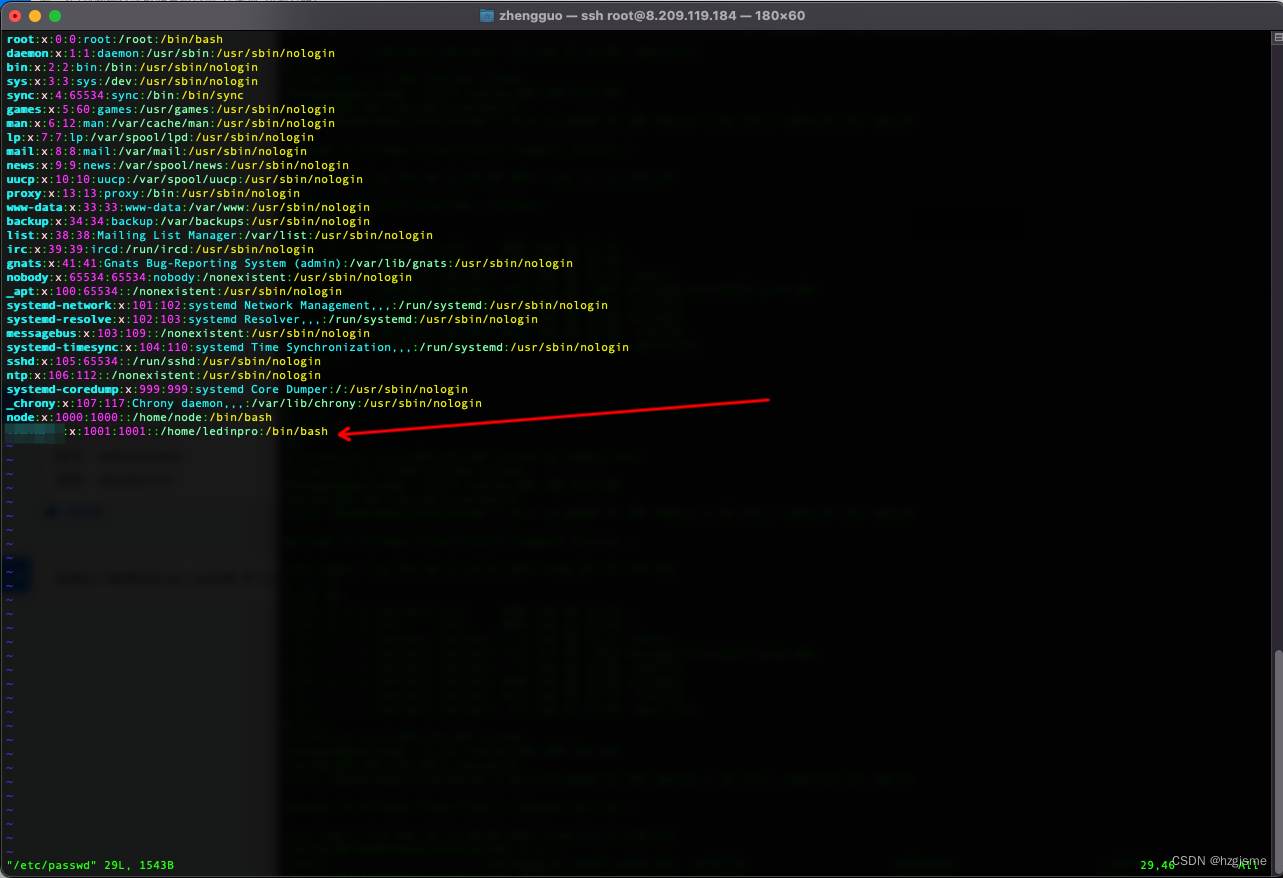
Linux 常见问题
1. 使用 sudo 命令时,提示 is not in the sudoers file. 是由于对应用户没有添加到 sudoers 文件中,可以在该文件中指定用户权限。运行以下命令即可打开该文件: visudo 添加上对应用户的权限 Ctrl x 退出保存即可。 2. Debian 新建的普通用…...

仕达利恩飞讯软件TPM设备管理项目正式启动,向数字化再迈一步
9月25日,仕达利恩(惠州)科技有限公司(以下简称“仕达利恩”)设备智能数采项目启动会成功召开,仕达利恩首席崔浩渊、杨翠琼次长携项目主要负责人共同出席本次启动会。为解决仕达利恩现阶段生产过程中的设备管理、设备配件仓管理以及…...
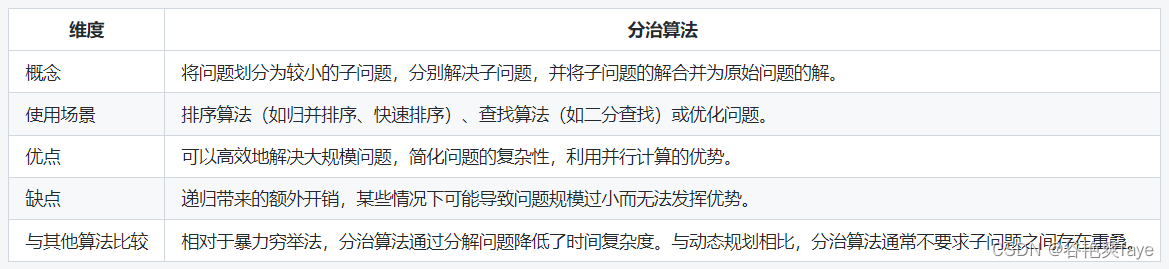
【算法】分治法
文章目录 概念原理和步骤代码示例 总结 概念 分治法(Divide and Conquer)是一种算法设计策略,其思想是将一个大问题划分为若干小规模的子问题,然后递归地解决每个子问题,并将它们的解合并起来以得到原始问题的解。分治…...
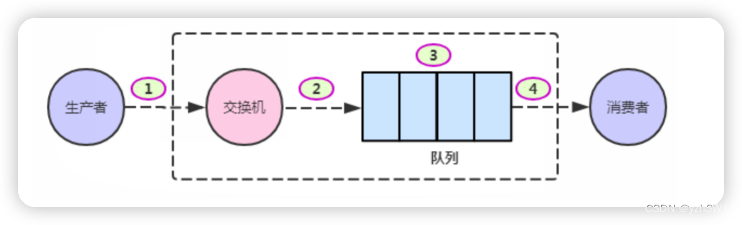
Rabbit消息的可靠性
生产者重连 消费者重试 Confirm模式简介 消息的confirm确认机制,是指生产者投递消息后,到达了消息服务器Broker里面的exchange交换机,则会给生产者一个应答,生产者接收到应答,用来确定这条消息是否正常的发送到Broker…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
