【初阶数据结构】二叉树全面知识总结
二叉树详解
- 树的概念及其结构
- 树的概念
- 树的相关概念
- 树的表示方法
- 孩纸兄弟表示法
- 双亲表示法(并查集)
- 树的实际应用
- 二叉树
- 二叉树的概念
- 二叉树的种类
- 二叉树的性质
- 二叉树的存储结构
- 二叉树顺序结构的实现
- 堆的概念及结构
- 堆向上、向下调整法
- 堆的插入
- 堆的删除
- 堆的创建
- 堆实现总代码
- 建堆时间复杂度的证明
- 堆排序
- TopK问题
- 二叉树链式结构的实现
- 创建二叉树
- 前序遍历及其实现
- 中序遍历及其实现
- 后序遍历及其实现
- 销毁二叉树
- 求二叉树的高度
- 求二叉树总节点个数
- 求二叉树叶子节点个数
- 求二叉树第k层节点个数
- 二叉树查找值为x的节点
- 二叉树总代码实现
- 层序遍历
- 判断是否为二叉树
- 总代码
铁汁们,今天给大家分享一篇二叉树全面知识总结,来吧,开造⛳️
树的概念及其结构
树的概念
树的概念:是一种非线性的数据结构,它由n个有限的节点组成的一个具有层次关系的集合。树的结构类似于真实世界中的树,它看起来就像一颗倒挂着的树,即:它的根是朝上的,而叶子是朝下的。


说明:
1.有一个特殊的节点,根节点,该节点没有父节点(前驱节点);
2.根节点除外,其他节点被分成了M个互不相交的集合{a1, a2, a3…},每个集合又是一颗结构类似的子树(每个子树又可以被分成根节点、左子树、右子树)——》递归思想,把大事化小,树是递归定义的;
3.其他节点都有一个父节点(前驱节点),并且可以有零个或多个子节点(后继节点)。一个节点可以有一个或多个子节点,但每个节点最多只能有一个父节点 ——》说明子树是不相交的。

注意:树形结构中,子树之间不能有交集,否则就不是树形结构。
树的相关概念

树的表示方法
树形结构的线性表:树在进行存储时,既要保存值域,也要保存各个节点之间的关系。
树的表示方法:双亲表示法、孩纸兄弟表示法、孩纸表示法、孩纸双亲表示法等(多叉树)。
孩纸兄弟表示法
孩纸兄弟表示法:让根节点指向第一个节点,让第一个节点指向靠的最近的兄弟节点,依次往后,直到无兄弟节点和兄弟节点无第一个节点。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>typedef int DataType;typedef struct Node //孩纸兄弟表示法
{struct Node* firstchild; struct Node* secondchild;DataType val; //值域
}Node;int main()
{Node* parent; //从根节点开始Node* child = parent->firstchild; //让根节点指向第一个节点while (child) {printf("%d ", child->val);child = child->secondchild; //第一个节点指向靠的最近的兄弟节点}return 0;
}

双亲表示法(并查集)

//c++实现代码:#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream> //合并查集(最基本版:用来1.合并两个集合, 2.查找两个数是否在一个集合内)using namespace std;const int N = 1e5 + 10;
//每个集合都用一个树来表示,树的编号就是整个集合的编号,每个数都有个树根。每个节点用来存储其父节点,p[x]表示节点x的父节点
//判断每个集合的树根,p[x] == x
//求x的集合编号,while(p[x] != x) x = p[x];
//将两个集合编号合并,因px是x的集合编号,py是y的集合编号,p[x] = y(让x所在的集合变为y所在集合的儿子)或者p[y] = x(让y所在的集合变为x所在集合的儿子)
int p[N];int find(int x) //查找每个数的树根(集合编号)+路径压缩(因每个节点均向上找树根,当一个节点找到了树根,则该节点所在的路径上所有的点父节点直接等于树根)
{if (p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) p[i] = i; //因每个数都在不同的集合中,让集合的编号的本身(p[x] == x,树根)while (m--){char op[2];int a, b;cin >> op >> a >> b;if (*op == 'I') p[find(a)] = find(b); //两个集合的合并else //判断两数所在的集合是否相同,即:判断树根值是否向他{if (find(a) == find(b)) printf("YES\n"); //相同else printf("NO\n"); //不相同}}return 0;
}
树的实际应用
树的应用:用于表示文件系统的目录,表示方法为孩子兄弟法。



二叉树
二叉树的概念
二叉树定义:是由有限节点组成的集合,该集合可能为空(空树),或不为空(由一个根节点加上左子树和右子树组成)。
注意:
1.二叉树度小于等于2。
2.二叉树不存在度大于2的节点。
3.二叉树有左、右子树之分,次序不能颠倒,所以二叉树也为有序树。
二叉树都是由以下几种情况的树复合而成的:

二叉树的种类
特殊的二叉树:满二叉树、完全二叉树。
1.满二叉树:
一个二叉树,每一层节点达到了最大值(度等于2),则这个二叉树为满二叉树。

注意:满二叉树高度为h,满二叉树总结点树为2^n-1个。
现实生活中的满二叉树:

2.完全二叉树:
二叉树深度为n,1.我是文本 红色red前n-1层结点数都要达到最大值(度为2),最后一层结点数不一定达到最大值,但最后一层节点一定是从左到右排布的。完全二叉树是一种特殊的满二叉树。

注意:完全二叉树的总结点个数范围为[ 2^(n-1), 2^n-1]。
二叉树的性质

题目:

二叉树的存储结构
二叉树一般可分为两种结构存储,一种为顺序存储,一种为链式存储。
1.顺序存储
顺序结构存储数据实质就是用数组来存储,一般数组只适用于存储满二叉树、完全二叉树,若存储普通的二叉树则会造成空间浪费,堆、栈、顺序表均为顺序存储结构,均用数组来存储数据。二叉树顺序存储在逻辑结构上是一颗二叉树(想象出来的结构),在 color = red>物理结构上是一个数组(实际存在的)。

2.链式存储
二叉树链式存储:
用链表来表示二叉树节点之间的逻辑关系,通常链表中每个节点由三个域组成,数据域和左、右指针域,左、右指针域分别存储该节点的左、右孩子的地址,根节点通过其左右子节点指针连接到左右子树,子节点可以依次连接到它们的子树。链式结构又可以分为二叉链、三叉链。
二叉链:
每个节点包含数据元素和指向左右子节点的指针。通过这个指针,可以实现从子节点到父节点的访问。二叉链结构使得在树中的任意节点上,能够直接访问其父节点,方便进行反向操作。但要注意,根节点的父节点指针为空。
三叉链:
每个节点除了包含数据元素和指向左右子节点的指针之外,还包含一个指向父节点的指针。三叉链结构使得在树中的任意节点上,能够同时访问其父节点和子节点,方便进行各种树的操作。
二叉树顺序结构的实现
堆的概念及结构
堆:堆中所有的元素按完全二叉树的顺序全部存储到一维数组中,当根节点的值<=左、右子树的根节点的值,任意父亲节点值<=左、右孩纸节点的值,则该堆为小堆;当根节点的值>=左、右子树的根节点的值,任意父亲节点值>=左、右孩纸节点的值,则该堆为大堆。
注意:堆的性质:
1.任意父亲节点值<=(或者>=)左、右孩纸节点的值。
2.堆的逻辑结构为完全二叉树(堆是一颗完全二叉树),物理结构为数组。

堆向上、向下调整法
给出一个数组,就可以画出其对应得完全二叉树,通过向上或向下调整法可以将其调整为一个小堆。
向上、向下调整法使用前提:左、右子树必须都为堆。
向上调整法:从根节点的左结点开始,从左到右依次调整每一层的所有节点形成堆。
void AdjustUp(HPDataType* a, int child) //(使用前提:左、右子树均为堆)向上调整,从根节点的左结点开始,数据从上往下依次向上调整形成堆
{int parent = (child - 1) / 2; //父亲节点(找父亲节点)while (child > 0) //{if (a[child] < a[parent]) //该节点与父节点值进行比较swap(&a[child], &a[parent]); //交换,形成小堆child = parent; //递归parent = (child - 1) / 2;}
}

向下调整法:从最后一个非叶子节点开始,数据从下往上依次向下调整每个节点形成堆。
void AdjustDown(int* a, int n, int parent) //(使用前提:根的左、右子树均为堆)向下调整,从最后一个非叶子节点开始,数据从下往上依次向下调整形成堆
{int child = parent * 2 + 1; //孩纸节点,初始化左孩子值比右孩纸值小(找孩纸节点)while (child < n) //{if (child + 1 < n && a[child] > a[child + 1]) //左、右孩纸值进行比较,确保右孩纸存在,且左孩子值比右孩纸值大swap(&a[child], &a[child + 1]); //交换,此时child节点中的值为孩纸节点的最小值if (a[child] < a[parent]) //左孩子值与父节点值进行比较swap(&a[child], &a[parent]); //交换,形成小堆parent = child; //递归child = parent * 2 + 1;}
}

堆的插入
思路:将数据直接插入到最后一个位置,新插入的元素在向上调整。
void HeapPush(Heap* hp, HPDataType x) //向堆中插入一个元素
{assert(hp); //断言,不能对空指针进行加、减、解引用操作if (hp->size == hp->capacity) //空间满了,不能进行插入数据,如需插入数据,需要realloc进行扩容{int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2; //新容量HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity); if (tmp == NULL) //realloc开辟失败{perror("realloc failed");exit(-1);}hp->a = tmp; //realloc开辟成功hp->capacity = newcapacity; //容量进行更新为新容量}hp->a[hp->size] = x; //在末尾插入一个元素hp->size++;AdjustUp(hp->a, hp->size - 1); //在将新插入的元素进行向上调整形成堆
}
堆的删除
思路:将堆中最后一个元素覆盖堆顶元素,堆顶元素在向下调整。
void HeapPop(Heap* hp) //删除堆顶元素
{assert(hp); //断言,不能对空指针进行加、减、解引用操作hp->a[0] = hp->a[hp->size-1]; //将最后一个元素覆盖堆顶元素hp->size--; AdjustDown(hp->a, hp->size, 0); //在将堆顶元素进行向下调整形成堆
}
堆的创建
void HeapCreat(Heap* hp, int* b, int n) //建堆(堆的创建)
{assert(hp && b); //断言,不能对空指针进行加、减、解引用操作hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n); //malloc动态开辟数组空间 if (hp->a == NULL) //malloc动态开辟失败{perror("malloc failed");exit(-1); //异常退出,终止程序,(非0值表示不正常退出,0表示正常退出)}memcpy(hp->a, b, sizeof(HPDataType) * n); //此处需要将已知的数组建成堆,将数组中所有值拷贝给动态开辟的数组hp->size = hp->capacity = n; for (int i = (n-2)/2; i >= 0; i--) //向下调整法建堆,从倒数第一个非叶子节点开始调整,层数依次向上,每层从右到左遍历每个节点,每个节点都向下调整AdjustDown(hp->a, n, i);
}
堆实现总代码
Heap.h
#pragma once //用数组来模拟实现堆(顺序表实现)#include<stdio.h>
#include<stdlib.h> //malloc
#include<assert.h> //assert
#include<string.h> //memcpytypedef int HPDataType; typedef struct HeapNode //动态版
{HPDataType* a; //malloc动态开辟数组空间,存储每个节点的值int size; //表示堆中实际有效节点的总个数int capacity; //容量
}Heap;//传址调用,此处只需要改变结构体中的成员变量,只需要传结构体的地址,形参为一级指针(顺序表),若需要改变结构体的地址,则形参为二级指针(单链表)。void HeapCreat(Heap* hp, int* b, int n); //建堆(堆的创建)void HeapPush(Heap* hp, HPDataType x); //向堆中插入一个元素void HeapDestory(Heap* hp); //销毁void HeapPop(Heap* hp); //删除堆顶元素HPDataType HeapTop(Heap* hp); //获取堆顶元素int HeapSize(Heap* hp); //获取堆中有效节点的总个数int HeapEmpty(Heap* hp); //判断堆是否为空void HeapPrint(Heap* hp); //打印堆中节点的值
Heap.c
#define _CRT_SECURE_NO_WARNINGS 1#include"Heap.h"void swap(int* p1, int* p2) //交换两元素的值,传址调用,传值调用(形参的改变不会影响实参的改变)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(int* a, int n, int parent) //(使用前提:根的左、右子树均为堆)向下调整,从最后一个非叶子节点开始,数据从下往上依次向下调整形成堆
{int child = parent * 2 + 1; //孩纸节点,初始化左孩子值比右孩纸值小while (child < n) //{if (child + 1 < n && a[child] > a[child + 1]) //左、右孩纸值进行比较,确保右孩纸存在,且左孩子值比右孩纸值大swap(&a[child], &a[child + 1]); //交换,此时child节点中的值为孩纸节点的最小值if (a[child] < a[parent]) //左孩子值与父节点值进行比较swap(&a[child], &a[parent]); //交换,形成小堆parent = child; //递归child = parent * 2 + 1;}
}void AdjustUp(HPDataType* a, int child) //(使用前提:左、右子树均为堆)向上调整,从根节点的左结点开始,数据从上往下依次向上调整形成堆
{int parent = (child - 1) / 2; //父亲节点while (child > 0) //{if (a[child] < a[parent]) //该节点与父节点值进行比较swap(&a[child], &a[parent]); //交换,形成小堆child = parent; //递归parent = (child - 1) / 2;}
}void HeapCreat(Heap* hp, int* b, int n) //建堆(堆的创建)
{assert(hp && b); //断言,不能对空指针进行加、减、解引用操作hp->a = (HPDataType*)malloc(sizeof(HPDataType) * n); //malloc动态开辟数组空间 if (hp->a == NULL) //malloc动态开辟失败{perror("malloc failed");exit(-1); //异常退出,终止程序,(非0值表示不正常退出,0表示正常退出)}memcpy(hp->a, b, sizeof(HPDataType) * n); //此处需要将已知的数组建成堆,将数组中所有值拷贝给动态开辟的数组hp->size = hp->capacity = n; for (int i = (n-2)/2; i >= 0; i--) //向下调整法建堆,从倒数第一个非叶子节点开始调整,层数依次向上,每层从右到左遍历每个节点,每个节点都向下调整AdjustDown(hp->a, n, i);
}void HeapPush(Heap* hp, HPDataType x) //向堆中插入一个元素
{assert(hp); //断言,不能对空指针进行加、减、解引用操作if (hp->size == hp->capacity) //空间满了,不能进行插入数据,如需插入数据,需要realloc进行扩容{int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2; //新容量HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity); if (tmp == NULL) //realloc开辟失败{perror("realloc failed");exit(-1);}hp->a = tmp; //realloc开辟成功hp->capacity = newcapacity; //容量进行更新为新容量}hp->a[hp->size] = x; //在末尾插入一个元素hp->size++;AdjustUp(hp->a, hp->size - 1); //在将新插入的元素进行向上调整形成堆
}void HeapDestory(Heap* hp) //销毁
{assert(hp);//断言,不能对空指针进行加、减、解引用操作free(hp->a); //释放malloc动态开辟的空间hp->a = NULL; //防止该空间被其他变量存储了该地址,通过该地址访问此空间,不能访问已经释放的空间,会造成野指针hp->size = hp->capacity = 0;
}void HeapPop(Heap* hp) //删除堆顶元素
{assert(hp); //断言,不能对空指针进行加、减、解引用操作hp->a[0] = hp->a[hp->size-1]; //将最后一个元素覆盖堆顶元素hp->size--; AdjustDown(hp->a, hp->size, 0); //在将堆顶元素进行向下调整形成堆
}HPDataType HeapTop(Heap* hp) //获取堆顶元素
{return hp->a[0];
}int HeapSize(Heap* hp) //获取堆中有效节点的总个数
{return hp->size;
}int HeapEmpty(Heap* hp) //判断堆是否为空,为空,则为true,不为空,则为false
{if (hp->size > 0) return 0;else return 1;
}void HeapPrint(Heap* hp) //打印堆中节点的值
{assert(hp);for (int i = 0; i < hp->size; i++) //遍历堆中元素(通过数组的下标来遍历完全二叉树中的每个节点)printf("%d ", hp->a[i]);printf("\n");
}Test.c
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once#include"Heap.h"int main()
{Heap hp;int b[4] = { 3, 2, 1 ,4};int n = sizeof(b) / sizeof(int);HeapCreat(&hp, b, n);HeapPrint(&hp);for (int i = 0; i < 5; i++){int x;scanf("%d", &x);HeapPush(&hp, x);}HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);printf("%d\n", HeapTop(&hp));printf("%d\n", HeapSize(&hp));if (HeapEmpty(&hp))printf("YES\n");elseprintf("NO\n");HeapDestory(&hp);return 0;
}

建堆时间复杂度的证明

堆排序
注意:在进行堆排序建堆时:升序,建大堆、 降序,建小堆。
原因:堆排序是为了对数组进行排序,不是进行打印数组,便于进行其他一系列操作。
排升序,如果建小堆,只可以第一次获得最小的数,若要将剩余的元素进行排升序,只能将剩余的元素看成个堆,但各个元素对应的节点之间的关系已全部打乱,需要将剩余的元素重新建成堆,代价太大,时间复杂度为O(n*longn)。
排升序,建大堆,将第一个最大的数与最后一个元素进行交换,个数减1,在从剩余的n-1个找出次大的数,在与最后一个元素交换,个数减1,如此反复,时间复杂度为O(nlong)。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>void swap(int* p1, int* p2) //传址调用,形参的改变会影响实参的改变
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void down(int* a, int n, int parent) //向下调整法建堆,建大堆
{int child = parent * 2 + 1; //左孩纸节点while (child < n) //边界{if (child + 1 < n && a[child] < a[child + 1])//找到左孩纸与右孩纸节点中的最大值swap(&a[child], &a[child + 1]);if(a[parent] < a[child]) //建大堆swap(&a[child], &a[parent]);parent = child; //循环处理child = parent * 2 + 1;}
}void Heapsort(int* a, int n) //堆排序,对数组进行排序,升序,建大堆
{for (int i = (n - 2) / 2; i >= 0; i--) //向下调整法建堆,从下标为(i-1-1)/2的节点开始down(a, n, i);int end = n - 1; //最后一个元素所对应的下标值while (end > 0){swap(&a[0], &a[end]); //堆中最大的树与最后一个树进行交换down(a, end, 0); //将剩余的n-1个元素建大堆end--;}for (int i = 0; i < 6; i++) printf("%d ", a[i]);}int main()
{int a[6];for (int i = 0; i < 6; i++)scanf("%d", &a[i]);Heapsort(a, sizeof(a) / sizeof(int)); //堆排序return 0;
}

TopK问题
TopK问题:
求数据中的前k个大的数或者前k个小的数,该数据个数的范围非常的大,一般情况是建个堆,但在内存中不能一次性将所有数据全部加载到内存中,此时考虑将数据存入文件中,即:在文件中找TopK问题,实际应用场景:世界前500名富豪,游戏中前100名活跃的玩家等。
在文件中找前K个大的数:
1.将所有数据先存入文件中去,在从文件中读取,建成前K个数小堆。
2.在依次将文件中剩余的数据读取,每读取一个数,分别与堆中第一个树进行比较,比它大,两数据值进行交换,该数往下沉建成小堆,如此反复,最终堆中的K个数为文件中最大的前K个数。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h> //malloc, srand
#include<time.h> //time(时间戳)void swap(int* p1, int* p2) //传址调用
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustDown(int* a, int n, int parent) //(使用前提:根的左、右子树均为堆)向下调整,从最后一个非叶子节点开始,数据从下往上依次向下调整形成堆
{int child = parent * 2 + 1; //孩纸节点,初始化左孩子值比右孩纸值小while (child < n) //{if (child + 1 < n && a[child] > a[child + 1]) //左、右孩纸值进行比较,确保右孩纸存在,且左孩子值比右孩纸值大swap(&a[child], &a[child + 1]); //交换,此时child节点中的值为孩纸节点的最小值if (a[child] < a[parent]) //左孩子值与父节点值进行比较swap(&a[child], &a[parent]); ///交换,形成小堆parent = child; //递归child = parent * 2 + 1;}
}void CreatNData() //在文件中创造数据
{int n = 100000;const char* file = "data.txt"; FILE* fin = fopen(file, "w"); //以写的方式将文件打开if (fin == NULL) //文件打开失败{perror("fopen failed");exit(-1); //异常退出,终止程序(负数)}for (int i = 0; i < n; i++) //创造n个随机数{int x = rand() % 10000; //数据值得范围为0~9999fprintf(fin, "%d\n", x); //将n个树写到文件中("%d\n",每个数据占一行)}fclose(fin); //关闭文件
}/*思路:一、从文件中读出k个数据放在数组中(fscanf,有格式),将k个数建成小堆(不可以是大堆,最大的数据会堵在堆顶不下去)
* 二、依次将文件中剩余的n-k个数据读取过来,与堆顶进行比较,大于,则往下沉
* 此时堆中剩余的k个数为最大的前k个数(且为升序)
*/
void HeapTopK(int k) //topk
{const char* file = "data.txt";FILE* fout = fopen(file, "r"); //以读的方式将文件打开if (file == NULL) //文件打开失败{perror("fopen failed");exit(-1); //异常退出,终止程序(负数)}//一、从文件中读出k个数据放在数组中(fscanf,有格式),将k个数建成小堆(不可以是大堆,最大的数据会堵在堆顶不下去)int* mink = (int*)malloc(sizeof(int) * k); //malloc创造一个动态数组用来存储文件中的前k个数if (mink == NULL) //malloc开辟失败{perror("malloc failed");exit(-1);//异常退出,终止程序(负数)}for (int i = 0; i < k; i++) //从文件中读出k个数据fscanf(fout, "%d", &mink[i]); for (int i = (k-2)/2; i >= 0; i--)//将k个数建成小堆AdjustDown(mink, k, i);// 二、依次将文件中剩余的n - k个数据读取过来,与堆顶进行比较,大于,则往下沉int x = 0;while (fscanf(fout, "%d", &x) != EOF)//将文件中剩余的n - k个数据读取{ //fscanf返回值为读取的个数,读取失败或者读取为NULL,则返回EOF(~EOF(-1)== 0)if (x > mink[0]) //与堆顶进行比较,大于,则往下沉mink[0] = x;AdjustDown(mink, k, 0);}for (int i = 0; i < k; i++)printf("%d ", mink[i]);free(mink); //释放malloc动态开辟的空间mink = NULL;fclose(fout); //关闭文件
}int main()
{srand((unsigned int)time(NULL)); //生成随机数srand~time~rand//CreatNData(); //创造数据int k;scanf("%d", &k); //topkHeapTopK(k);return 0;
}




二叉树链式结构的实现
创建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* i) //由前序遍历将数组中的值创建二叉树
{ if (a[*i] == '#') // '#'代表空节点{(*i)++; //数组向后走一位,构建下一个节点return NULL; }BTNode* root = (BTNode*)malloc(sizeof(BTNode)); //malloc动态开辟内存,创建新节点if (root == NULL) //malloc动态开辟失败{perror("malloc failed"); exit(-1); //终止程序,异常退出,0表示正常退出,非0表示异常退出}root->val = a[*i]; //数组中值不为空,将该值赋给新节点(*i)++; //数组向后走一位,构建下一个节点//该节点的左、右节点均创建完成,该节点在其左、右节点进行链接root->left = BinaryTreeCreate(a, n, i); //递归处理创建左节点,左节点遇到空,递归结束root->right = BinaryTreeCreate(a, n, i); //递归处理创建右节点,右节点遇到空,递归结束return root; //返回树的根节点
}

前序遍历及其实现
void BinaryTreePrevOrder(BTNode* root) //前序遍历,根、左、右
{if (root == NULL) //空树return ;printf("%c ", root->val); //根BinaryTreePrevOrder(root->left); //递归处理左BinaryTreePrevOrder(root->right); //递归处理右
}
中序遍历及其实现
void BinaryTreeInOrder(BTNode* root) //中序遍历,左、根、右
{if (root == NULL) //空树return;BinaryTreeInOrder(root->left); //递归处理左printf("%c ", root->val); //根BinaryTreeInOrder(root->right); //递归处理右
}
后序遍历及其实现
void BinaryTreePostOrder(BTNode* root) //后序遍历,左、右、根
{if (root == NULL) //空树return;BinaryTreePostOrder(root->left); //递归处理左BinaryTreePostOrder(root->right); //递归处理右printf("%c ", root->val); //根
}
销毁二叉树
/*采用后序遍历,不可采用前序遍历,原因:销毁根节点之前需要存储左子树的根,便于可以找到左子树,也需要存储右子树的根,便于可以找到右子树*/
void BinaryTreeDestory(BTNode* root) //销毁,后序遍历
{if (root == NULL) //空树,未动态开辟任何节点return;BinaryTreeDestory(root->left); //递归处理左BinaryTreeDestory(root->right); //递归处理右free(root); //销毁根
}
求二叉树的高度
int BinaryTreeHeight(BTNode* root) //树的高度
{if (root == NULL) //空树return 0;int leftheight = BinaryTreeHeight(root->left); //左子树的高度int rightheight = BinaryTreeHeight(root->right); //右子树的高度return leftheight > rightheight ? leftheight + 1 : rightheight + 1; //找出左、右子树高度大的树+根(+1)
}
求二叉树总节点个数
int BinaryTreeSize(BTNode* root) //树的总节点个数,分治法、递归法(将其分为根、左子树、右子树,对应的子树又可以分成根、左、右子树)
{if (root == NULL) //空树return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; //左子树的节点+右子树的节点+根节点(+1)
}
求二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root) //树中叶子节点的个数,分治法、递归法(将其分为根、左子树、右子树,对应的子树又可以分成根、左、右子树)
{if (root == NULL) //空树return 0;if (root->left == NULL && root->right == NULL) //叶子节点的特征,该左、右节点均为空,则该节点为叶子节点return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right); //左子树叶子节点个数+右子树叶子节点个数
}
求二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k) //树中第k层节点的总个数,将第k层转换为1层,将k-1层转换为第2层..直到k==1,则为第k层
{if (root == NULL) //空树return 0;if (k == 1) //第k层return 1; return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) //在树中查找是否存在值为x的节点
{if (root == NULL) //空树return 0;if (root->val == x) //找到了return root;BTNode* ret = NULL; ret = BinaryTreeFind(root->left, x); //递归左子树if (ret) //若左子树找到了直接返回return ret;ret = BinaryTreeFind(root->right, x); //左子树找不到,在找右子树if (ret) //右子树找到了直接返回return ret;return NULL; //找不到
}二叉树总代码实现
BinaryTree.h
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<stdlib.h> //malloc
#include<string.h> //strlentypedef char BTDataType; //二叉树节点值的类型,适用于任意数据类型typedef struct BinaryTreeNode //树中的节点
{struct BinaryTreeNode* left; //指针域:左孩纸struct BinaryTreeNode* right; //右孩纸BTDataType val; //数据域
}BTNode;BTNode* BinaryTreeCreate(BTDataType* a, int n, int* i); //由前序遍历将数组中的值创建二叉树void BinaryTreePrevOrder(BTNode* root);//前序遍历,根、左、右void BinaryTreeInOrder(BTNode* root); //中序遍历,左、根、右void BinaryTreePostOrder(BTNode* root); //后序遍历,左、右、根void BinaryTreeDestory(BTNode *root); //销毁int BinaryTreeHeight(BTNode* root); //树的高度int BinaryTreeSize(BTNode* root); //树的总节点个数int BinaryTreeLeafSize(BTNode* root); //树中叶子节点的个数int BinaryTreeLevelKSize(BTNode* root, int k); //树中第k层节点的总个数BTNode* BinaryTreeFind(BTNode* root, BTDataType x); //在树中查找是否存在值为x的节点BinaryTree.c
#define _CRT_SECURE_NO_WARNINGS 1#include"BinaryTree.h"BTNode* BinaryTreeCreate(BTDataType* a, int n, int* i) //由前序遍历将数组中的值创建二叉树
{ if (a[*i] == '#') // '#'代表空节点{(*i)++; //数组向后走一位,构建下一个节点return NULL; }BTNode* root = (BTNode*)malloc(sizeof(BTNode)); //malloc动态开辟内存,创建新节点if (root == NULL) //malloc动态开辟失败{perror("malloc failed"); exit(-1); //终止程序,异常退出,0表示正常退出,非0表示异常退出}root->val = a[*i]; //数组中值不为空,将该值赋给新节点(*i)++; //数组向后走一位,构建下一个节点//该节点的左、右节点均创建完成,该节点在其左、右节点进行链接root->left = BinaryTreeCreate(a, n, i); //递归处理创建左节点,左节点遇到空,递归结束root->right = BinaryTreeCreate(a, n, i); //递归处理创建右节点,右节点遇到空,递归结束return root; //返回树的根节点
}void BinaryTreePrevOrder(BTNode* root) //前序遍历,根、左、右
{if (root == NULL) //空树return ;printf("%c ", root->val); //根BinaryTreePrevOrder(root->left); //递归处理左BinaryTreePrevOrder(root->right); //递归处理右
}void BinaryTreeInOrder(BTNode* root) //中序遍历,左、根、右
{if (root == NULL) //空树return;BinaryTreeInOrder(root->left); //递归处理左printf("%c ", root->val); //根BinaryTreeInOrder(root->right); //递归处理右
}void BinaryTreePostOrder(BTNode* root) //后序遍历,左、右、根
{if (root == NULL) //空树return;BinaryTreePostOrder(root->left); //递归处理左BinaryTreePostOrder(root->right); //递归处理右printf("%c ", root->val); //根
}
/*采用后序遍历,不可采用前序遍历,原因:销毁根节点之前需要存储左子树的根,便于可以找到左子树,也需要存储右子树的根,便于可以找到右子树*/
void BinaryTreeDestory(BTNode* root) //销毁,后序遍历
{if (root == NULL) //空树,未动态开辟任何节点return;BinaryTreeDestory(root->left); //递归处理左BinaryTreeDestory(root->right); //递归处理右free(root); //销毁根
}int BinaryTreeSize(BTNode* root) //树的总节点个数,分治法、递归法(将其分为根、左子树、右子树,对应的子树又可以分成根、左、右子树)
{if (root == NULL) //空树return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1; //左子树的节点+右子树的节点+根节点(+1)
}int BinaryTreeLeafSize(BTNode* root) //树中叶子节点的个数,分治法、递归法(将其分为根、左子树、右子树,对应的子树又可以分成根、左、右子树)
{if (root == NULL) //空树return 0;if (root->left == NULL && root->right == NULL) //叶子节点的特征,该左、右节点均为空,则该节点为叶子节点return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right); //左子树叶子节点个数+右子树叶子节点个数
}int BinaryTreeLevelKSize(BTNode* root, int k) //树中第k层节点的总个数,将第k层转换为1层,将k-1层转换为第2层..直到k==1,则为第k层
{if (root == NULL) //空树return 0;if (k == 1) //第k层return 1; return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}BTNode* BinaryTreeFind(BTNode* root, BTDataType x) //在树中查找是否存在值为x的节点
{if (root == NULL) //空树return 0;if (root->val == x) //找到了return root;BTNode* ret = NULL; ret = BinaryTreeFind(root->left, x); //递归左子树if (ret) //若左子树找到了直接返回return ret;ret = BinaryTreeFind(root->right, x); //左子树找不到,在找右子树if (ret) //右子树找到了直接返回return ret;return NULL; //找不到
}int BinaryTreeHeight(BTNode* root) //树的高度
{if (root == NULL) //空树return 0;int leftheight = BinaryTreeHeight(root->left); //左子树的高度int rightheight = BinaryTreeHeight(root->right); //右子树的高度return leftheight > rightheight ? leftheight + 1 : rightheight + 1; //找出左、右子树高度大的树+根(+1)
}
Test.c
#define _CRT_SECURE_NO_WARNINGS 1#include"BinaryTree.h"int main()
{BTDataType arr[] = "ABD##E#H##CF##G##"; int n = strlen(arr);int j = 0;BTNode* root = BinaryTreeCreate(arr, n, &j); //由前序遍历将数组中的值创建二叉树BinaryTreePrevOrder(root); //前序遍历printf("\n");BinaryTreeInOrder(root); //中序遍历printf("\n");BinaryTreePostOrder(root); //后序遍历printf("\n");printf("%d\n", BinaryTreeHeight(root)); //树的高度printf("%d\n",BinaryTreeSize(root)); //树的总节点个数printf("%d\n", BinaryTreeLeafSize(root)); //树中叶子节点的个数printf("%d\n", BinaryTreeLevelKSize(root, 3)); //树中第k层节点的总个数BTNode* ret = BinaryTreeFind(root, 'F'); //在树中查找是否存在值为x的节点if (ret != NULL) printf("找到了\n"); elseprintf("找不到\n");BinaryTreeDestory(root); //销毁return 0;
}

层序遍历

void BinaryTreeLevelOrder(BTNode* root) //层次遍历,用队列实现,上一层带下一层,当上一层节点全部出队,则下一层所有节点均入队了
{Queue plist;QueueInit(&plist); //初始化队列,队列中用于存储树中的节点if (root == NULL) //空树return;QueuePush(&plist, root); //将根插入队列中while (!QueueEmpty(&plist)) //{BTNode* front = QueueFront(&plist); //获取队头元素printf("%d ", front->val); //打印树中节点的值if (front->left) //左孩纸不为空,空节点不能入队QueuePush(&plist, front->left); //将该节点的左孩子入队if (front->right) //右孩纸不为空,空节点不能入队QueuePush(&plist, front->right); //将该节点的右孩子入队QueuePop(&plist); //删除队头元素}printf("\n");QueueDestroy(&plist); //二叉树的销毁
}
判断是否为二叉树

int BinaryTreeComplete(BTNode* root) //判断其是否为二叉树,最后一层非空节点从左到右连续分布
{Queue plist;QueueInit(&plist); //初始化队列,队列中用于存储树中的节点if (root == NULL) //空树return;QueuePush(&plist, root); //将根插入队列中while (!QueueEmpty(&plist)) //{BTNode* front = QueueFront(&plist); //获取队头元素if (front == NULL) //队头为空节点break;QueuePush(&plist, front->left); //左孩纸入队,空节点也需入队QueuePush(&plist, front->right); //右孩纸入队,空节点也需入队QueuePop(&plist); //删除非空节点}while (!QueueEmpty(&plist)) //{BTNode* front = QueueFront(&plist); //获取队头元素QueuePop(&plist); //删除队头节点if (front != NULL) //队头为非空节点{QueueDestroy(&plist); return false; //不是完全二叉树}QueuePop(&plist); //删除队头节点}QueueDestroy(&plist); //销毁return true; //是完全二叉树printf("\n");
}
总代码
Tset.c
#define _CRT_SECURE_NO_WARNINGS 1#include"Queue.h"/*void test()
{Queue plist;QueueInit(&plist);QueuePush(&plist, 1);QueuePush(&plist, 2);QueuePush(&plist, 3);QueuePush(&plist, 4);QueuePush(&plist, 5);QueuePush(&plist, 6);while (!QueueEmpty(&plist)){printf("%d ", QueueFront(&plist));QueuePop(&plist);}printf("\n");QueueDestroy(&plist);
}int main()
{test(); //测试队列,先进先出return 0;
}
*/
BTNode* BuyNode(int x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->left = NULL;root->right = NULL;root->val = x;return root;
}void BinaryTreeLevelOrder(BTNode* root)
{Queue plist;QueueInit(&plist);if (root == NULL)return;QueuePush(&plist, root);while (!QueueEmpty(&plist)){BTNode* front = QueueFront(&plist);printf("%d ", front->val);if (front->left)QueuePush(&plist, front->left);if (front->right)QueuePush(&plist, front->right);QueuePop(&plist);}printf("\n");QueueDestroy(&plist);
}int BinaryTreeComplete(BTNode* root)
{Queue plist;QueueInit(&plist);if (root == NULL)return;QueuePush(&plist, root);while (!QueueEmpty(&plist)){BTNode* front = QueueFront(&plist);if (front == NULL)break;QueuePush(&plist, front->left);QueuePush(&plist, front->right);QueuePop(&plist);}while (!QueueEmpty(&plist)){BTNode* front = QueueFront(&plist);QueuePop(&plist); //if (front != NULL){QueueDestroy(&plist);return false;}QueuePop(&plist);}QueueDestroy(&plist);return true;printf("\n");
}int main()
{BTNode* n1 = BuyNode(1);BTNode* n2 = BuyNode(6);BTNode* n3 = BuyNode(7);BTNode* n4 = BuyNode(2);BTNode* n5 = BuyNode(3);BTNode* n6 = BuyNode(4);BTNode* n7 = BuyNode(5);n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;BinaryTreeLevelOrder(n1);if (BinaryTreeComplete(n1))printf("是完全二叉树\n");elseprintf("不是完全二叉树\n");return 0;
}Queue.c
#define _CRT_SECURE_NO_WARNINGS 1#include"Queue.h"void QueueInit(Queue* p) //初始化
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作p->front = NULL;p->rear = NULL;p->size = 0;
}void QueuePush(Queue* p, QDataType x) //入队
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作QNode* newnode=(QNode*)malloc(sizeof(QNode)); //malloc动态开辟新的节点if (newnode == NULL) //开辟空间失败{perror("malloc"); //报错原因exit(-1); //终止程序,异常结束}newnode->data = x; newnode->next = NULL;if (p->rear == NULL) //注意:头插(特殊处理),链表为空{p->front = p->rear = newnode;}else //尾插 ,需要找尾节点{p->rear->next = newnode; p->rear=p->rear->next;}p->size++; //链表中有效元素个数加+
}bool QueueEmpty(Queue* p) //判断队列是否为空
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作return p->front == NULL; //为空,则为真,返回非0值,若不为空,为假,则返回0
}void QueuePop(Queue* p) //出队
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作assert(!QueueEmpty(p)); //断言,链表为空,则不能进行删除 if (p->front->next == NULL) //注意:当链表中只剩一个元素,因为尾指针、头指针同时指向该节点,释放该节点,需要将尾指针、头指针都置成NULL,否则会造成野指针(指向已经被释放的空间){free(p->front);p->front = p->rear = NULL;}else //链表中剩余至少有1个元素{QNode* next = p->front->next;free(p->front);p->front = next;}p->size--; //链表中有效元素个数加-
}QDataType QueueFront(Queue* p) //获取队头元素
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作assert(!QueueEmpty(p)); //断言,链表为空,则不能获取到队头的元素return p->front->data;
}QDataType QueueBack(Queue* p) //获取队尾元素
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作assert(!QueueEmpty(p)); //断言,链表为空,则不能获取到队尾的元素return p->rear->data;
}int QueueSize(Queue* p) //获取队列中有效元素的个数
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作assert(!QueueEmpty(p)); //断言,链表为空,则不能获取到有效元素的总个数return p->size;
}void QueueDestroy(Queue* p) //销毁
{assert(p); //断言,检查指针的有效性,防止对空指针进行解引用,加减操作while (p->front) //遍历链表{QNode* next = p->front->next;free(p->front);p->front = next;}p->front = p->rear = NULL;p->size = 0;
}
Queue.h
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<stdlib.h> //malloc
#include<assert.h> //assert
#include<stdbool.h> //bool类型typedef struct BinaryTreeNode* QDataType;typedef int BTDataType;typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType val;
}BTNode;typedef struct QueueNode //链式结构:表示队列
{QDataType data; struct QueueNode* next;
}QNode;typedef struct Queue //队列结构
{QNode* front; //队头QNode* rear; //队尾int size; //有效元素个数
}Queue;void QueueInit(Queue* p); //初始化
void QueuePush(Queue* p, QDataType x); //入队
void QueuePop(Queue* p); //出队
QDataType QueueFront(Queue* p); //获取队头元素
QDataType QueueBack(Queue* p); //获取队尾元素
int QueueSize(Queue* p); //获取队列中有效元素的个数
bool QueueEmpty(Queue* p); //判断队列是否为空
void QueueDestroy(Queue* p); //销毁

铁铁们,二叉数全面知识总结就到此结束啦,若博主有不好的地方,请指正,欢迎铁铁们留言,请动动你们的手给作者点个👍鼓励吧,你们的鼓励就是我的动力✨
相关文章:

【初阶数据结构】二叉树全面知识总结
二叉树详解 树的概念及其结构树的概念树的相关概念树的表示方法孩纸兄弟表示法双亲表示法(并查集) 树的实际应用 二叉树二叉树的概念二叉树的种类二叉树的性质二叉树的存储结构 二叉树顺序结构的实现堆的概念及结构堆向上、向下调整法堆的插入堆的删除堆…...
CMD命令终端快捷键学习
很多环境需要安装并且指定环境变量才可用终端访问 比如一些数据库、一些环境、例如:nodejs Oracle、mysql 在一个文件夹按住shift鼠标右键可以快速在当前目录运行终端!免去cd 目录的烦恼 快捷键 当你学习和使用命令终端(如 Windows 的 CMD&…...

Leetcode198. 打家劫舍
https://leetcode.cn/problems/house-robber/description/ 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入&…...

前端技术社区总目录
前端技术社区欢迎您的订阅。订阅后,您将可以查看以下所有博客内容。 注:专栏内容主要面向新手 注:每个示例都有相对应的完整代码 注:该专栏博客内容将会逐步迁移至https://blog.csdn.net/m0_60387551/article/details/128017725 …...

极客时间:左耳听风【文章笔记 思考总结】
本篇博客是学习过程中的笔记、思考和总结。原文链接:https://time.geekbang.org/column/intro/100002201 开篇词 | 洞悉技术的本质,享受科技的乐趣01 | 程序员如何用技术变现(上)02 | 程序员如何用技术变现(下…...

《论文阅读27》SuperGlue: Learning Feature Matching with Graph Neural Networks
一、论文 研究领域: 图像特征点匹配论文:SuperGlue: Learning Feature Matching with Graph Neural NetworksCVPR 2020veido论文code 二、论文简述 [参考] [参考] [参考] 三、论文详述 SuperGlue:使用图神经网络学习特征匹配 本文介绍了…...
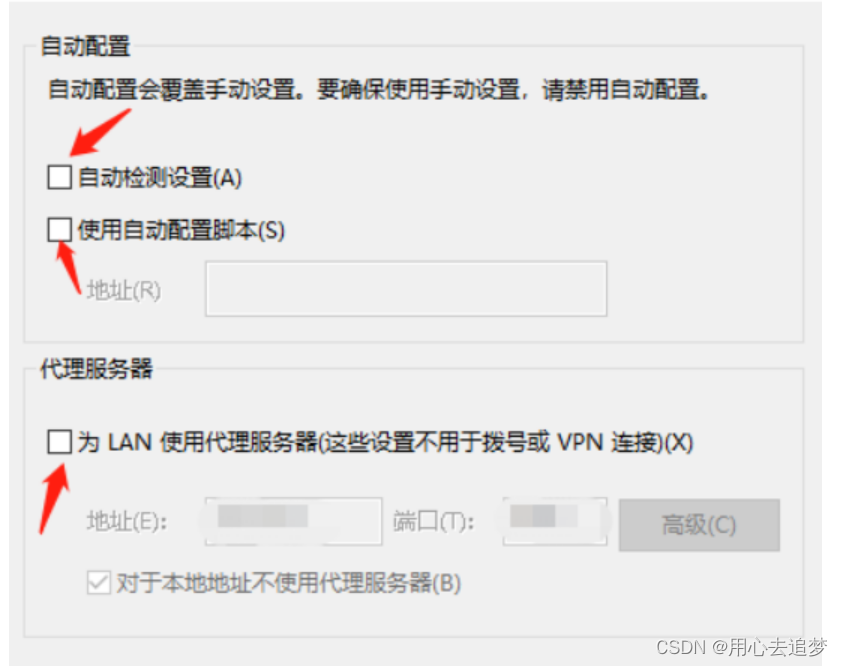
远程计算机或设备不接受连接解决方法
远程计算机或设备不接受连接解决方法 点击左下角开始,点击运行,输入inetcpl.cpl,点击确定,打开Internet选项。 将三个框的勾勾去掉,即为不选中状态,点击确定。 当你的电脑浏览器不能正常上网时ÿ…...
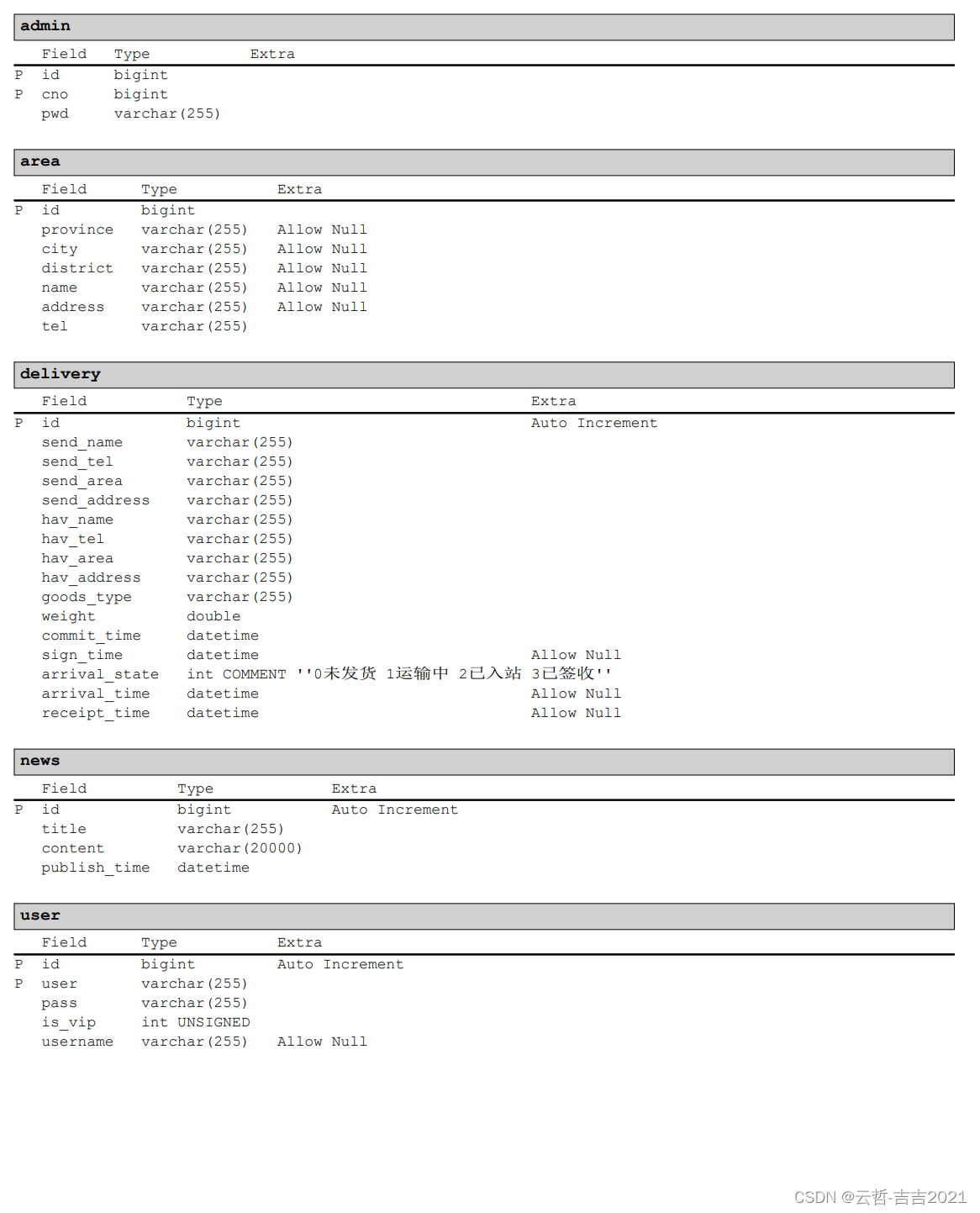
基于Python实现的快递管理系统源码+数据库,采用PyQt6实现GUI界面
快递管理系统 完整代码下载地址:快递管理系统 介绍 通过对传统的快递收发流程进行分析,完成网上快递管理系统的分析设计与开发,使客户能方便在网站上查询自己的快件信息以及网上寄件,同时管理员又能对每天的收到快件进行登记和…...
如何使用docker快速部署MinDoc文档系统
MinDoc是非常优秀的知识分享系统,但是很多刚接触的人会一脸懵逼,而且官方文档写的也并不清晰,所以和大家分享一下快速部署MinDoc的方法。 首先docker环境先自行安装好,这里不再赘述。 拉取docker镜像: docker pull …...

9月25日,每日信息差
今天是2023年9月27日,以下是为您准备的18条信息差 第一、苹果向法国监管机构提交iPhone 12软件更新,解决辐射超标问题 第二、“双节”期间,北京全市预计接待游客1283万人次,中秋国庆“双节”长假将至,北京市民和游客…...

【网络协议】Https
HTTP 协议内容都是按照⽂本的⽅式明⽂传输的,这就可能导致在传输过程中出现⼀些被篡改的情况。所以在HTTP协议的基础上,引入加密层,形成了HTTPS协议。 HTTPS 协议是由 HTTP 加上 TLS/SSL 协议构建的可进行加密传输、身份认证的网络协议,主要…...
Elasticsearch模板与索引设置)
Lostash同步Mysql数据到Elasticsearch(三)Elasticsearch模板与索引设置
logstash数据同步ES相关 同步数据时,Elasticsearch配合脚本的相关处理设置 1.模板创建更新 在kibana中执行,或者直接给ES发送请求,你懂得,不懂得百度下ES创建template PUT /_template/test-xxx {"template": "…...
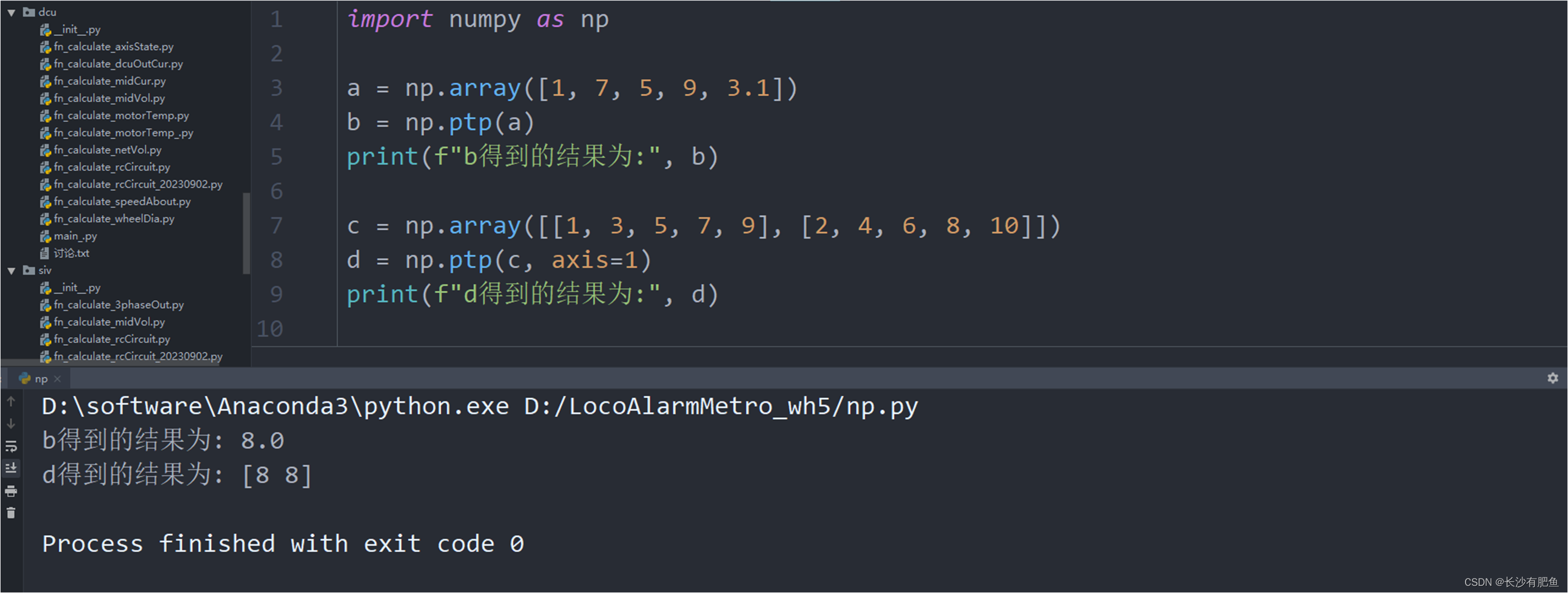
python——ptp()函数
函数功能:求最大值和最小值的差值 def ptp(a, axisNone, outNone):"""沿轴的值范围(最大值-最小值)。该函数的名称来自“peak-to-peak”的首字母缩写。参数----------a:array_like输入值。axis:int,可选找到山峰的…...
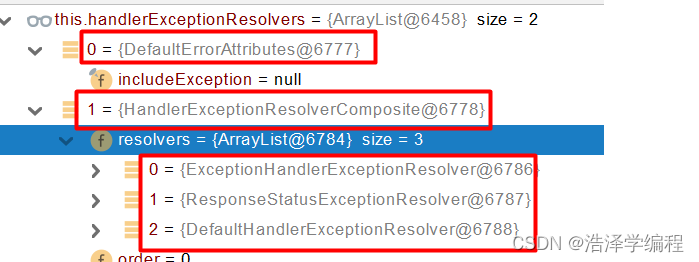
SpringBoot之异常处理
文章目录 前言一、默认规则二、定制异常处理处理自定义错误页面ControllerAdviceExceptionHandler处理全局异常ResponseStatus自定义异常自定义实现 HandlerExceptionResolver 处理异常 三、异常处理自动配置原理四、异常处理流程总结 前言 包含SpringBoot默认处理规则、如何定…...
: flask-socketio文档学习)
Flask-[实现websocket]-(2): flask-socketio文档学习
一、简单项目的构建 flask_websocket |---static |---js |---jquery-3.7.0.min.js |---socket.io_4.3.1.js |---templates |---home |---group_chat.html |---index.html |---app.py 1.1、python环境 python3.9.0 1.2、依赖包 Flask2.1.0 eventlet0.33.3 #使用这个性能会…...

网页中使用的图片格式
网页中使用的图片格式有以下几种,各有优缺点: JPEG:适用于照片或彩色图像,支持16.7万种颜色,有损压缩,可以调节压缩比和质量,文件较小,加载较快PNG:适用于图标或透明图像…...

【android】如何设置LD_LIBRARY_PATH?
目录 一 配置方法 1 进入Android shell 2 使用export命令 3 使用echo命令查看变量是否设置成功 二 扩展 1 LD_LIBRARY_PATH设置多个路径 2 push文件 一 配置方法 android中配置LD_LIBRARY_PATH的方法具体为: 1 进入Android shell adb shell 2 使用export…...
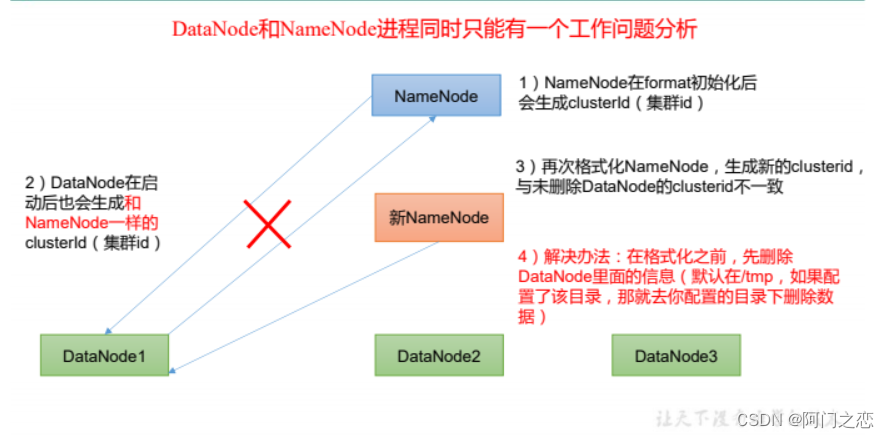
【hadoop3.x】一 搭建集群调优
一、基础环境安装 https://blog.csdn.net/fen_dou_shao_nian/article/details/120945221 二、hadoop运行环境搭建 2.1 模板虚拟机环境准备 0)安装模板虚拟机,IP 地址 192.168.10.100、主机名称 hadoop100、内存 4G、硬盘 50G 1)hadoop100…...
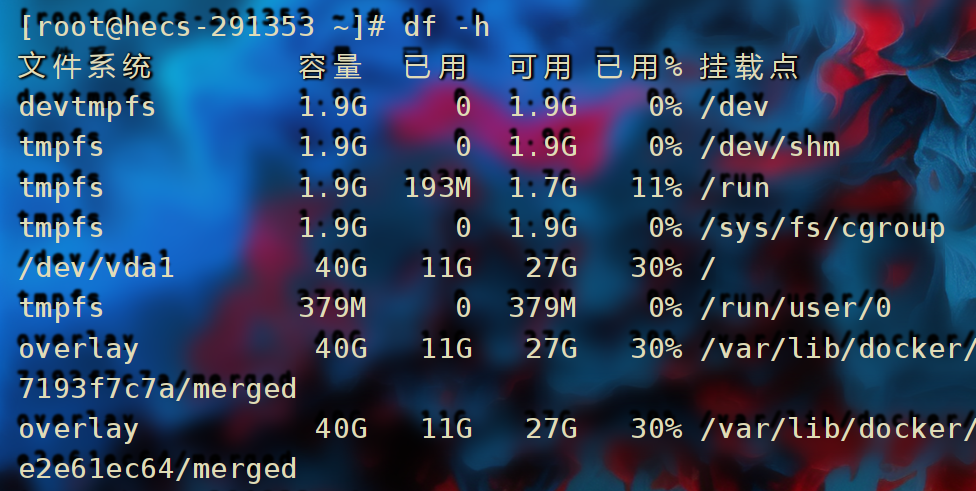
linux使用操作[2]
文章目录 版权声明网络传输ping命令wget命令curl命令端口linux端口端口命令和工具 进程管理查看进程关闭进程 主机状态top命令内容详解磁盘信息监控 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明,所有版权属于黑马程序员或相…...
华南理工大学电子与信息学院23年预推免复试面试经验贴
运气较好,复试分数90.24,电科学硕分数线84、信通83、专硕电子与信息74. 面试流程: 1:5min ppt的介绍。其中前2min用英语简要介绍基本信息,后3min可用英语也可用中文 介绍具体项目信息如大创、科研、竞赛等(…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
