数据结构与算法
目录
数据结构与算法
为什么要学习数据结构和算法?
常见的数据结构
常用算法
插入排序
一、概念及其介绍
二、适用说明
三、过程图示
希尔排序
一、概念及其介绍
二、适用说明
三、过程图示
归并排序
一、概念及其介绍
二、适用说明
三、过程图示
随机化快速排序
一、概念及其介绍
二、适用说明
三、过程图示
双路快速排序
一、概念及其介绍
二、适用说明
三、过程图示
三路排序算法
一、概念及其介绍
二、适用说明
排序算法衍生问题
(1)归并排序和快速排序都使用了分治算法。
(2)逆序对的定义
(3)取数组中第 n 大的元素
Reference Source:
数据结构与算法
数据结构(英语:data structure)是计算机中存储、组织数据的方式。
数据结构是一种具有一定逻辑关系,在计算机中应用某种存储结构,并且封装了相应操作的数据元素集合。它包含三方面的内容,逻辑关系、存储关系及操作。
不同种类的数据结构适合于不同种类的应用,而部分甚至专门用于特定的作业任务。例如,计算机网络依赖于路由表运作,B 树高度适用于数据库的封装。
为什么要学习数据结构和算法?
随着应用程序变得越来越复杂和数据越来越丰富,几百万、几十亿甚至几百亿的数据就会出现,而对这么大对数据进行搜索、插入或者排序等的操作就越来越慢,数据结构就是用来解决这些问题的。
常见的数据结构
- 栈(Stack):栈是一种特殊的线性表,它只能在一个表的一个固定端进行数据结点的插入和删除操作。
- 队列(Queue):队列和栈类似,也是一种特殊的线性表。和栈不同的是,队列只允许在表的一端进行插入操作,而在另一端进行删除操作。
- 数组(Array):数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地组织在一起的集合。
- 链表(Linked List):链表是一种数据元素按照链式存储结构进行存储的数据结构,这种存储结构具有在物理上存在非连续的特点。
- 树(Tree):树是典型的非线性结构,它是包括,2 个结点的有穷集合 K。
- 图(Graph):图是另一种非线性数据结构。在图结构中,数据结点一般称为顶点,而边是顶点的有序偶对。
- 堆(Heap):堆是一种特殊的树形数据结构,一般讨论的堆都是二叉堆。
- 散列表(Hash table):散列表源自于散列函数(Hash function),其思想是如果在结构中存在关键字和T相等的记录,那么必定在F(T)的存储位置可以找到该记录,这样就可以不用进行比较操作而直接取得所查记录。
常用算法
数据结构研究的内容:就是如何按一定的逻辑结构,把数据组织起来,并选择适当的存储表示方法把逻辑结构组织好的数据存储到计算机的存储器里。算法研究的目的是为了更有效的处理数据,提高数据运算效率。数据的运算是定义在数据的逻辑结构上,但运算的具体实现要在存储结构上进行。一般有以下几种常用运算:
- 检索:检索就是在数据结构里查找满足一定条件的节点。一般是给定一个某字段的值,找具有该字段值的节点。
- 插入:往数据结构中增加新的节点。
- 删除:把指定的结点从数据结构中去掉。
- 更新:改变指定节点的一个或多个字段的值。
- 排序:把节点按某种指定的顺序重新排列。例如递增或递减。
插入排序
一、概念及其介绍
插入排序(InsertionSort),一般也被称为直接插入排序。
对于少量元素的排序,它是一个有效的算法。插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增 1 的有序表
。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
二、适用说明
插入排序的平均时间复杂度也是 O(n^2),空间复杂度为常数阶 O(1),具体时间复杂度和数组的有序性也是有关联的。
插入排序中,当待排序数组是有序时,是最优的情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较 N-1 次,时间复杂度为 O(N)。最坏的情况是待排序数组是逆序的,此时需要比较次数最多,最坏的情况是 O(n^2)。
三、过程图示
假设前面 n-1(其中 n>=2)个数已经是排好顺序的,现将第 n 个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。
按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
从小到大的插入排序整个过程如图示:
第一轮:从第二位置的 6 开始比较,比前面 7 小,交换位置。
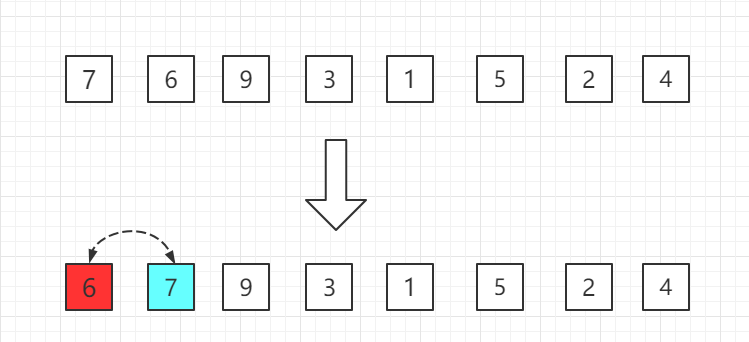
第二轮:第三位置的 9 比前一位置的 7 大,无需交换位置。

第三轮:第四位置的 3 比前一位置的 9 小交换位置,依次往前比较。

第四轮:第五位置的 1 比前一位置的 9 小,交换位置,再依次往前比较。
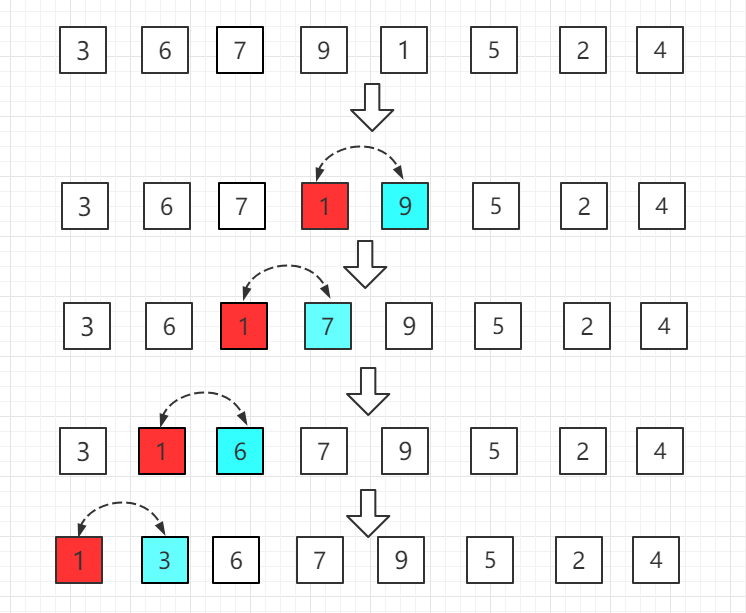
......
就这样依次比较到最后一个元素。
希尔排序
一、概念及其介绍
希尔排序(Shell Sort)是插入排序的一种,它是针对直接插入排序算法的改进。
希尔排序又称缩小增量排序,因 DL.Shell 于 1959 年提出而得名。
它通过比较相距一定间隔的元素来进行,各趟比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一趟排序为止。
二、适用说明
希尔排序时间复杂度是 O(n^(1.3-2)),空间复杂度为常数阶 O(1)。希尔排序没有时间复杂度为 O(n(logn)) 的快速排序算法快 ,因此对中等大小规模表现良好,但对规模非常大的数据排序不是最优选择,总之比一般 O(n^2 ) 复杂度的算法快得多。
三、过程图示
希尔排序目的为了加快速度改进了插入排序,交换不相邻的元素对数组的局部进行排序,并最终用插入排序将局部有序的数组排序。
在此我们选择增量 gap=length/2,缩小增量以 gap = gap/2 的方式,用序列 {n/2,(n/2)/2...1} 来表示。
如图示例:
(1)初始增量第一趟 gap = length/2 = 4
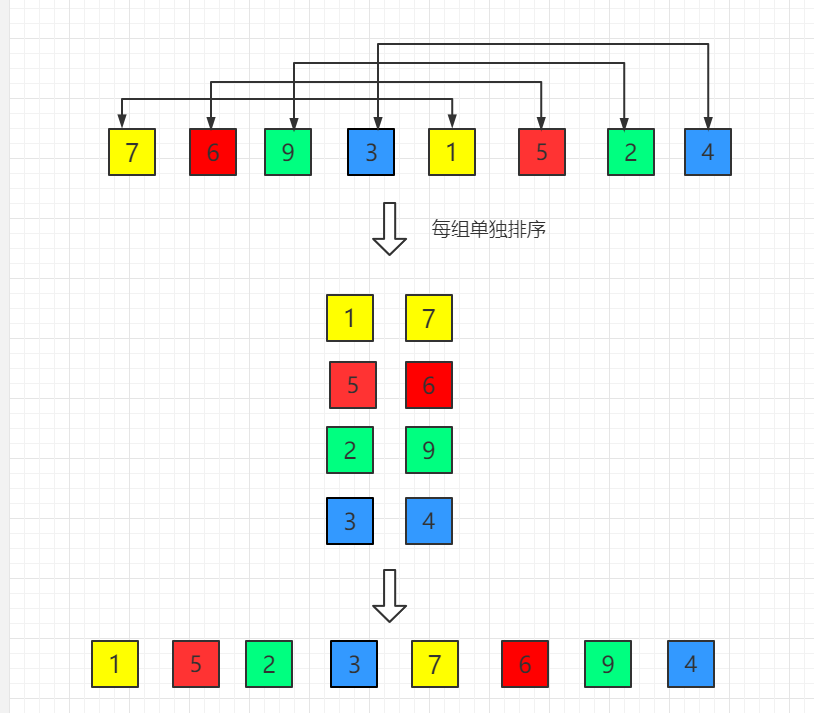
(2)第二趟,增量缩小为 2

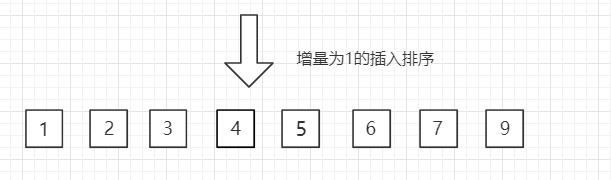
(3)第三趟,增量缩小为 1,得到最终排序结果
归并排序
一、概念及其介绍
归并排序(Merge sort)是建立在归并操作上的一种有效、稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
二、适用说明
当有 n 个记录时,需进行 logn 轮归并排序,每一轮归并,其比较次数不超过 n,元素移动次数都是 n,因此,归并排序的时间复杂度为 O(nlogn)。归并排序时需要和待排序记录个数相等的存储空间,所以空间复杂度为 O(n)。
归并排序适用于数据量大,并且对稳定性有要求的场景。
三、过程图示
归并排序是递归算法的一个实例,这个算法中基本的操作是合并两个已排序的数组,取两个输入数组 A 和 B,一个输出数组 C,以及三个计数器 i、j、k,它们初始位置置于对应数组的开始端。
A[i] 和 B[j] 中较小者拷贝到 C 中的下一个位置,相关计数器向前推进一步。
当两个输入数组有一个用完时候,则将另外一个数组中剩余部分拷贝到 C 中。
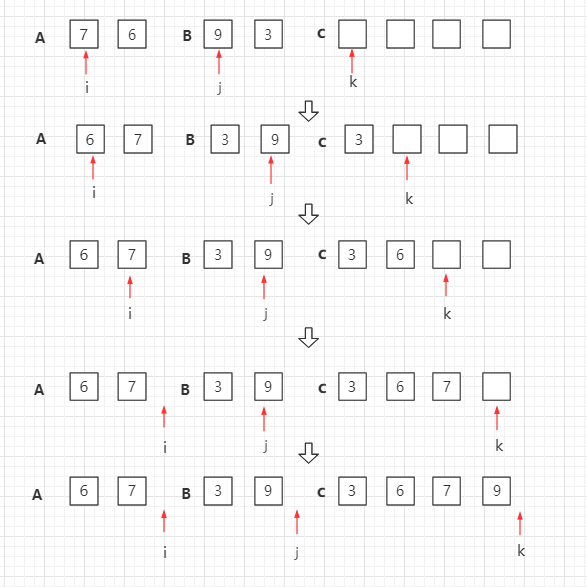
自顶向下的归并排序,递归分组图示:
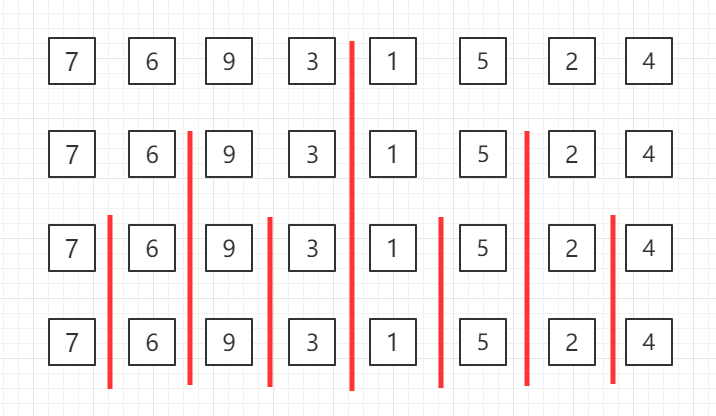
对第三行两个一组的数据进行归并排序
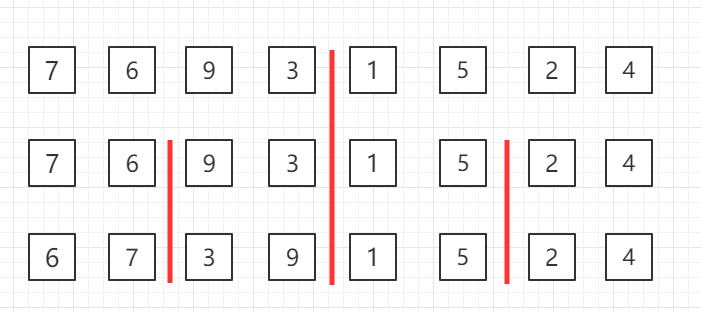
对第二行四个一组的数据进行归并排序
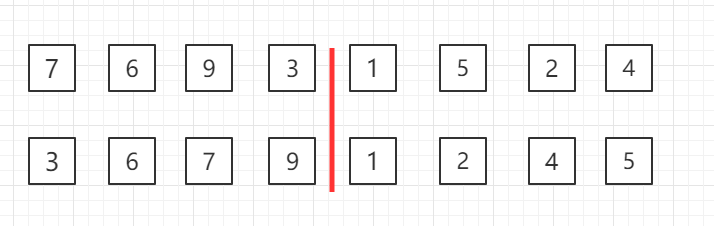
整体进行归并排序

随机化快速排序
一、概念及其介绍
快速排序由 C. A. R. Hoare 在 1960 年提出。
随机化快速排序基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
二、适用说明
快速排序是一种比较快速的排序算法,它的平均运行时间是 O(nlogn),之所以特别快是由于非常精练和高度优化的内部循环,最坏的情形性能为 O(n^2)。像归并一样,快速排序也是一种分治的递归算法。从空间性能上看,快速排序只需要一个元素的辅助空间,但快速排序需要一个栈空间来实现递归,空间复杂度也为O(logn)。
三、过程图示
在一个数组中选择一个基点,比如第一个位置的 4,然后把4挪到正确位置,使得之前的子数组中数据小于 4,之后的子数组中数据大于 4,然后逐渐递归下去完成整个排序。
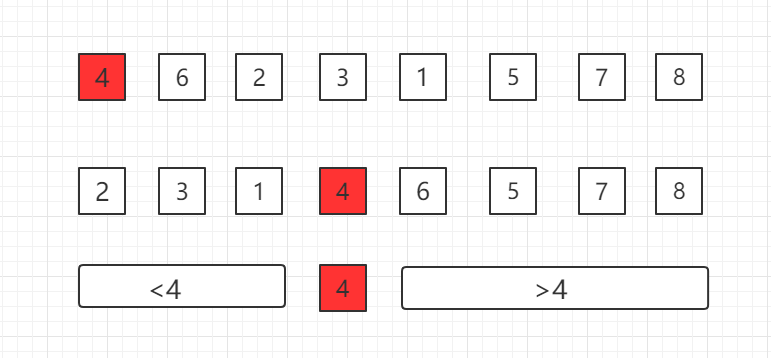
如何和把选定的基点数据挪到正确位置上,这是快速排序的核心,我们称为 Partition。
过程如下所示,其中 i 为当前遍历比较的元素位置:
如果是对近乎有序的数组进行快速排序,每次分区后子数组大小极不平衡,容易退化成 O(n^2) 的时间复杂度算法。我们需要对上述代码进行优化,随机选择一个基点做为比较,称为随机化快速排序算法。只需要在上述代码前加上下面一行,随机选择数组中一数据和基点数据进行交换。
swap( arr, l , (int)(Math.random()*(r-l+1))+l );
双路快速排序
一、概念及其介绍
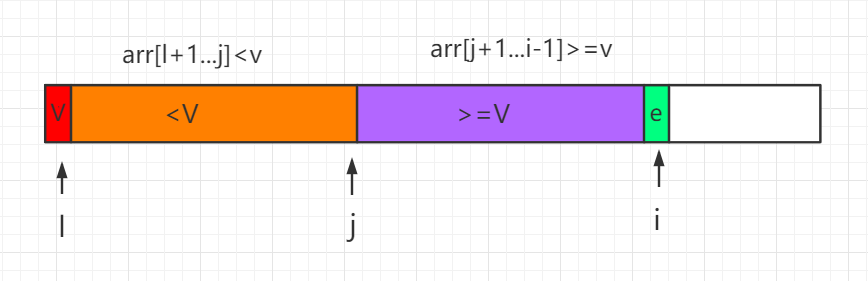
双路快速排序算法是随机化快速排序的改进版本,partition 过程使用两个索引值(i、j)用来遍历数组,将 <v 的元素放在索引i所指向位置的左边,而将 >v 的元素放在索引j所指向位置的右边,v 代表标定值。
二、适用说明
时间和空间复杂度同随机化快速排序。 对于有大量重复元素的数组,如果使用上一节随机化快速排序效率是非常低的,导致 partition 后大于基点或者小于基点数据的子数组长度会极度不平衡,甚至会退化成 O(n*2) 时间复杂度的算法,对这种情况可以使用双路快速排序算法。
三、过程图示
使用两个索引值(i、j)用来遍历我们的序列,将 <=v 的元素放在索引 i 所指向位置的左边,而将 >=v 的元素放在索引 j 所指向位置的右边,平衡左右两边子数组。

三路排序算法
一、概念及其介绍
三路快速排序是双路快速排序的进一步改进版本,三路排序算法把排序的数据分为三部分,分别为小于 v,等于 v,大于 v,v 为标定值,这样三部分的数据中,等于 v 的数据在下次递归中不再需要排序,小于 v 和大于 v 的数据也不会出现某一个特别多的情况),通过此方式三路快速排序算法的性能更优。
二、适用说明
时间和空间复杂度同随机化快速排序。
三路快速排序算法是使用三路划分策略对数组进行划分,对处理大量重复元素的数组非常有效提高快速排序的过程。它添加处理等于划分元素值的逻辑,将所有等于划分元素的值集中在一起。
三、过程图示
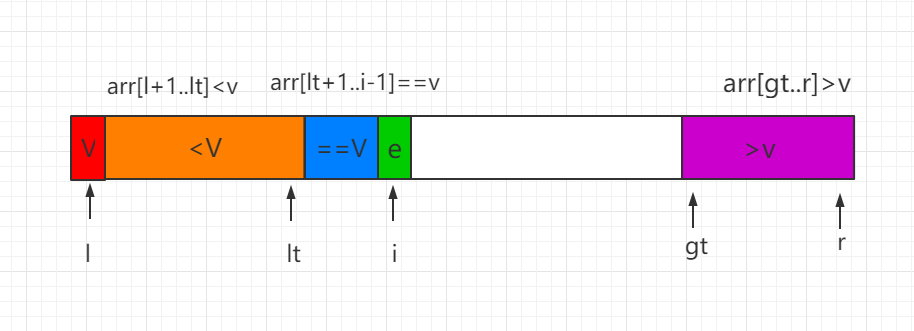
我们分三种情况进行讨论 partiton 过程,i 表示遍历的当前索引位置:
(1)当前处理的元素 e=V,元素 e 直接纳入蓝色区间,同时i向后移一位。
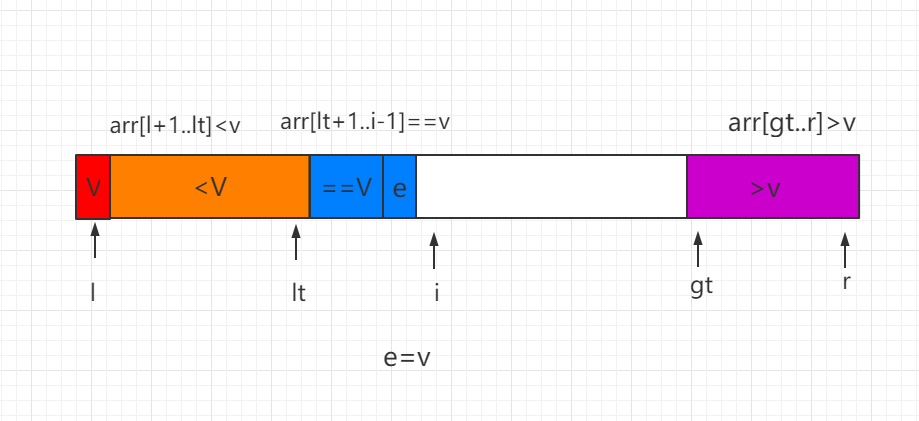
(2)当前处理元素 e<v,e 和等于 V 区间的第一个位置数值进行交换,同时索引 lt 和 i 都向后移动一位

(3)当前处理元素 e>v,e 和 gt-1 索引位置的数值进行交换,同时 gt 索引向前移动一位。
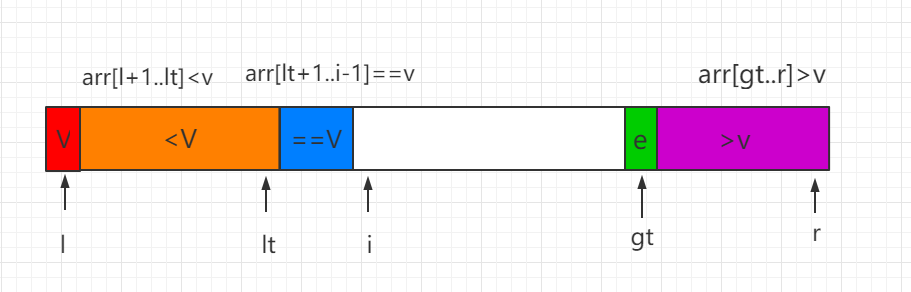
最后当 i=gt 时,结束遍历,同时需要把 v 和索引 lt 指向的数值进行交换,这样这个排序过程就完成了,然后对 <V 和 >V 的数组部分用同样的方法再进行递归排序。
排序算法衍生问题
本小节对本教程的排序算法做一个总结。
(1)归并排序和快速排序都使用了分治算法。
顾名思义,就是将原问题分割查能同等结构的子问题,之后将子问题逐一解决后,原问题也就得到了解决。
(2)逆序对的定义
如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j],则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对。我们可以使用本教程的归并思想求逆序对的数量。
(3)取数组中第 n 大的元素
并不需要对整个数组进行排序,使用快速排序的思路求数组中第 n 大元素算法复杂度为 O(n)。
Reference Source:
数据结构与算法 | 菜鸟教程
相关文章:

数据结构与算法
目录 数据结构与算法 为什么要学习数据结构和算法? 常见的数据结构 常用算法 插入排序 一、概念及其介绍 二、适用说明 三、过程图示 希尔排序 一、概念及其介绍 二、适用说明 三、过程图示 归并排序 一、概念及其介绍 二、适用说明 三、过程图示 …...
【Web3】DAO相关的基础知识
这里写目录标题 DAO 的基础概念为什么需要 DAO?DAO 的种类 DAO 的运作方式知名 DAO 的介绍Bankless DAOSeeDAO DAO 的生态全景图分类治理框架DAO 的工具 DAO 众筹平台介绍 - JuiceBoxDAO 投票治理介绍 - SnapshotDAO 贡献 & 激励 - POAPDAO 信息管理 - NotionDA…...

一文教你学会ArcGIS Pro地图设计与制图系列全流程(3)
ArcGIS Pro做的成果图及系列文章目录: 系列文章全集: 《一文教你学会ArcGIS Pro地图设计与制图系列全流程(1)》《一文教你学会ArcGIS Pro地图设计与制图系列全流程(2)》《一文教你学会ArcGIS Pro地图设计与…...
用于大规模 MIMO 检测的近似消息传递 (AMP)(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
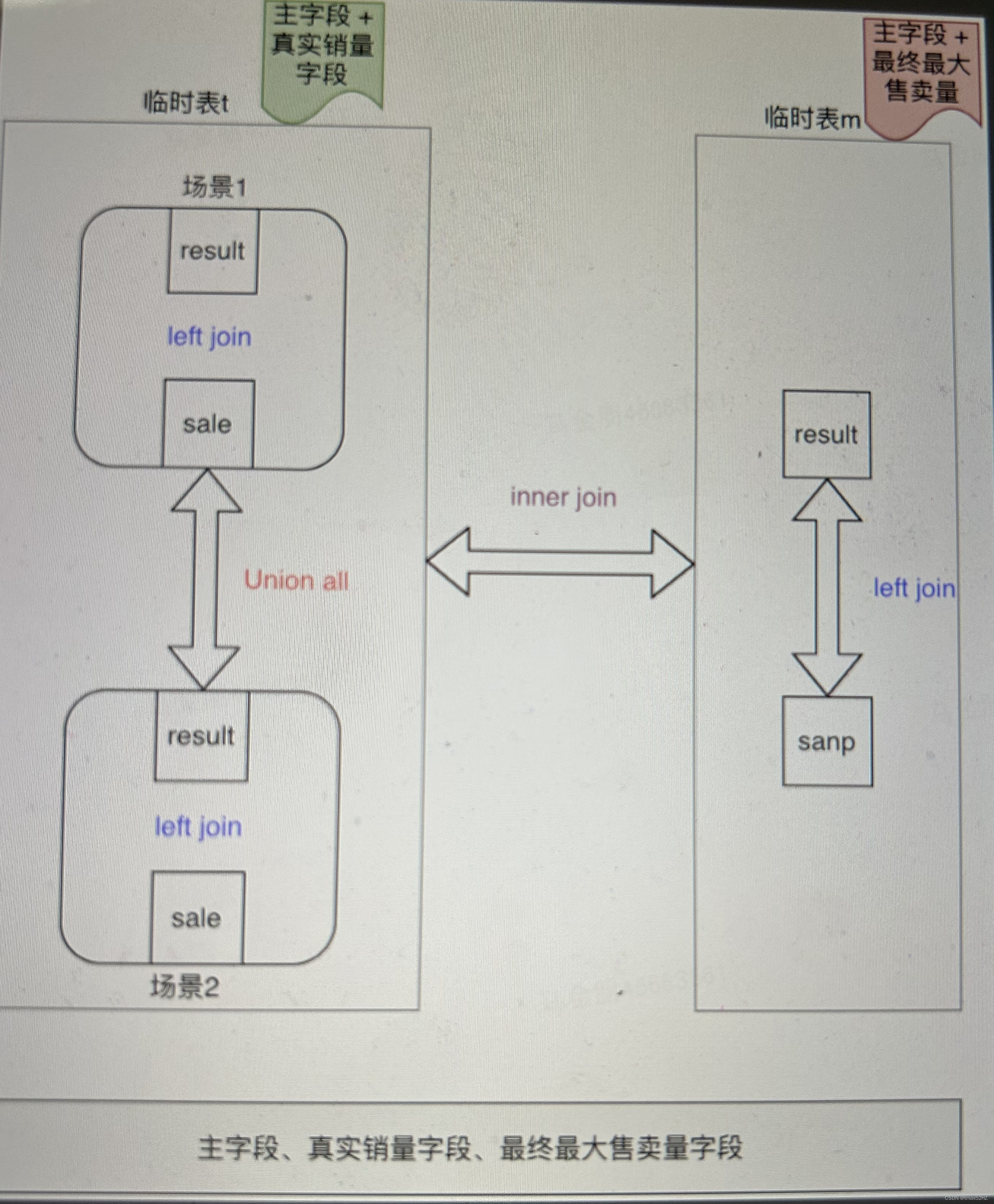
复杂SQL解析
文章目录 背景表SQL关键字分析具体Sql注意点补充:select的字段,也可以带有计算逻辑 背景表 1、sale_log as result: 主表,大部分字段都是取自这个表 2、sale_num as sale:需要从这个表获取真实销量sale_num字段 3、schedule as…...

js中哪些地方会用到window?
前言 Window 对象是JavaScript中的顶层对象,它代表了浏览器中打开的窗口或者标签页。浏览器中打开的每一个窗口/标签页都会有一个对应的 Window 对象。在浏览器中,全局作用域的 this 就是指向 Window 对象。 正文 在 JavaScript 中,window 对…...
KITTI raw_data数据集百度云下载
1. 百度云链接 链接:https://pan.baidu.com/s/1YNzfDoJomKOZhlVUr2eEOA?pwdtfh3 提取码:tfh3 –来自百度网盘超级会员V6的分享 2. 资料来源 https://www.cvlibs.net/datasets/kitti/raw_data.php 命令行执行./raw_data_downloader.sh #!/bin/bashfiles(2011_…...
 OpenCV图像处理kNN近邻算法)
(3) OpenCV图像处理kNN近邻算法
目录 一、介绍 1、类通过Matplotlib显示 2、Matplotlib显示效果 二、通过KNN近邻对新成员进行分类例程...
手撸RPC【gw-rpc】
文章目录 基于 Netty 的简易版 RPC需求分析简易RPC框架的整体实现协议模块 📖自定义协议 🆕序列化方式 🔢 服务工厂 🏭服务调用方 ❓前置知识——动态代理🕳️Proxy类InvocationHandler 接口 RPC服务代理类内嵌Netty客…...
【Linux】:Kafka组件介绍
目录 环境简介 一、消息 二、主题 三、分区 四、副本 五、生产者 六、消费者 七、消费者组 八、offsets【偏移量】 环境简介 Linux内核:Centos7 Kafka版本:3.5.1 执行命令的目录位置:Kafka安装目录的bin目录下:/usr/loca…...

Redis〔篇〕
redis怎么做到双写一致性呢? 这个是要分情况的 业务要是对一致性要求不是很高的话可以使用延时双删,要强一致的话需要双写一致性。 Redis数据持久化? redis是有两种数据持久化方式的,一种RDB一种AOF rdb是redis数据快照&#x…...
龙芯2K1000核心板在智能座舱行业产品方案-迅为电子
迅为2K1000核心板是一款高性能的处理器,适用于智能座舱行业。它具备多核CPU、高级图像处理和丰富的接口选项,可用于开发先进的智能座舱解决方案,提高乘坐体验、安全性和便捷性。以下是2K1000处理器在智能座舱行业中的产品方案。 高清晰度显…...
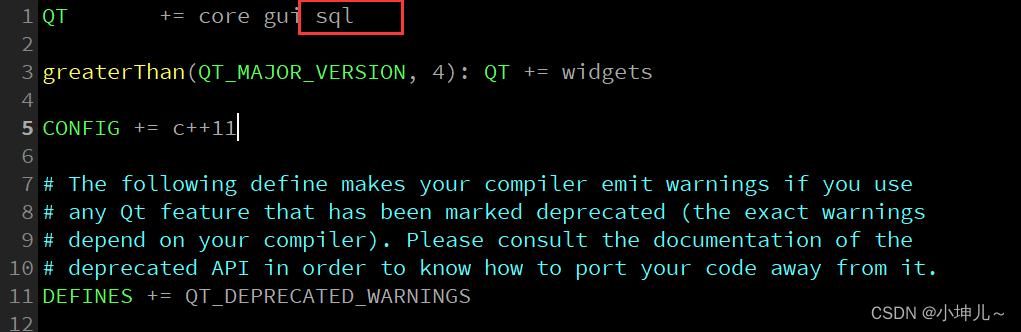
2023/9/20 -- C++/QT
时钟: widget.h: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPainter> #include <QPaintEvent> #include <QDateTime> #include <QLabel> #include <QTimer> #include <QDebug>QT_BEGIN_NAMESPACE namespac…...
WordPress主题DUX v8.2源码下载
新增产品分类左侧多级分类折叠显示 新增网站默认字体对 MiSans 和 HarmonyOS Sans 的支持 新增顶部左上角显示登录注册的模块开关,且支持原生登录方式 新增手机端导航菜单的关闭按钮 新增文章内容中标题二的强化展示 新增全站禁止复制、右键和选择的操作 新增文章内…...

c++图像的边缘检测
图像的边缘检测 cv::Canny 是 OpenCV 中用于进行边缘检测的函数,特别是用于检测图像中的边缘。Canny 边缘检测是一种广泛使用的技术,它能够识别图像中的边缘,这些边缘通常表示对象之间的边界或图像中的显著特征 void cv::Canny(const cv::M…...
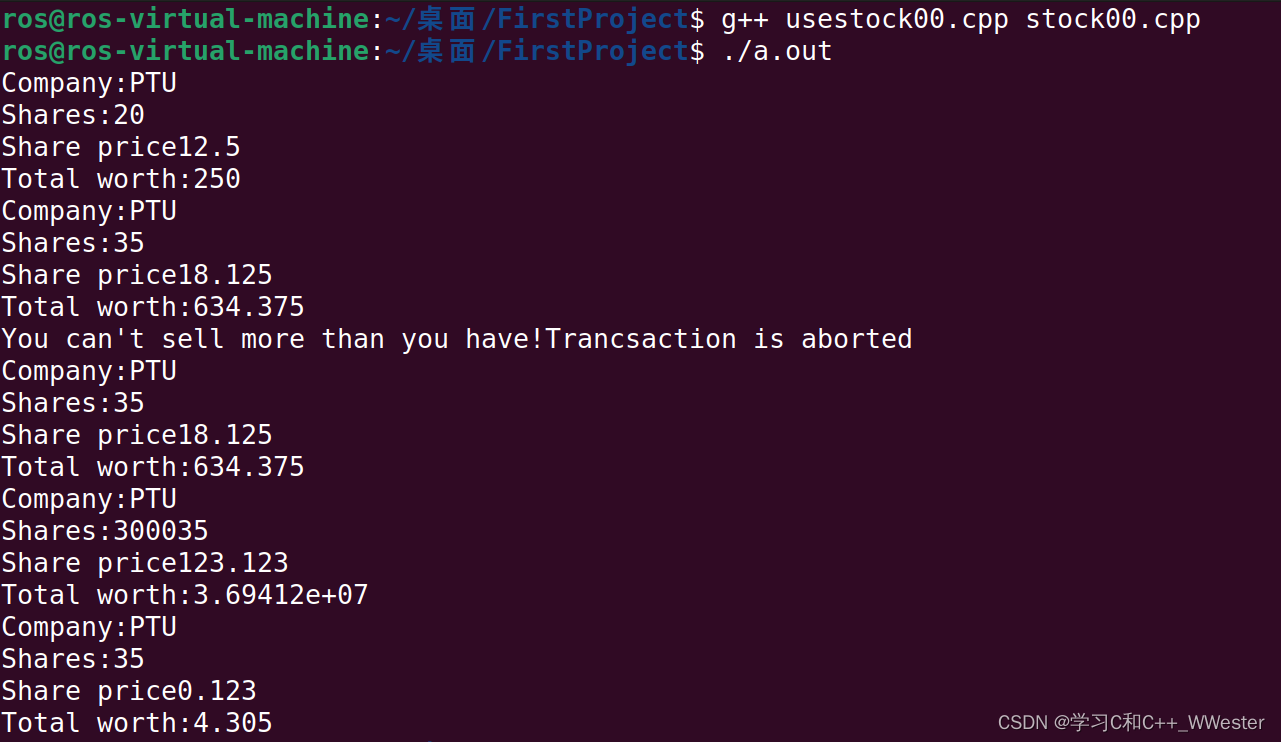
C++ Primer 类和对象(3)
类和结构体是比较相似,而传统的C的结构体中都是一些数据的类型,类除了有数据之外还有函数。所以可以把类想象成一个具有既有数据又有函数的复合数据类型。 类是一种将抽象转换为用户定义类型的C工具,它将数据表示和操纵数据的方法组合成一个整…...

IntelliJ IDEA 介绍、安装、配置优化与快捷键大全
一、简介 IDEA全称 IntelliJ IDEA,是Java编程语言的集成开发环境。IntelliJ在业界被公认为最好的Java开发工具,尤其在智能代码助手、代码自动提示、重构、JavaEE支持、各类版本工具(git、svn等)、JUnit、CVS整合、代码分析、 创新的GUI设计等方面的功能…...
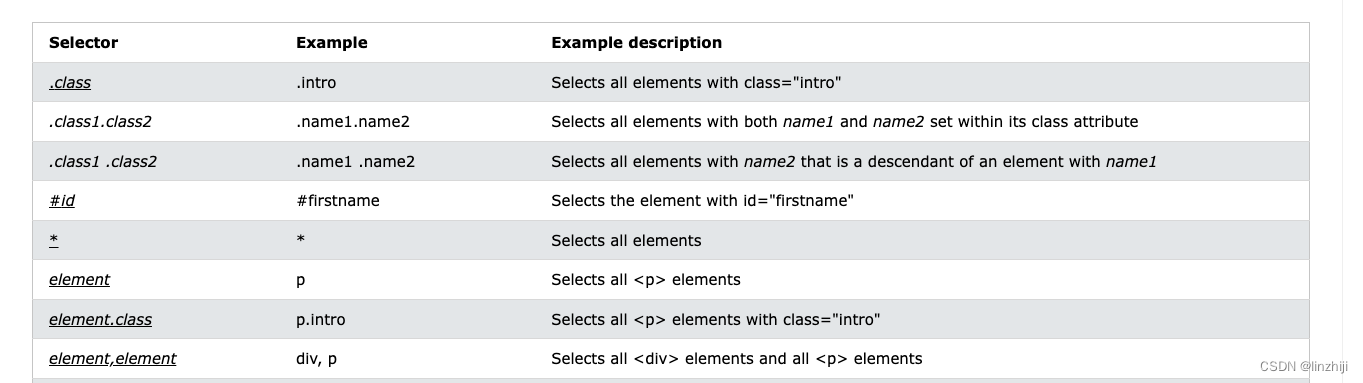
css 语法笔记
.abc {margin-left:20px; } .xyz {margin-left:20px; } 等同于 .abc, .xyz {margin-left: 20px; } 参考 CSS - 选择器_css最后一个元素选择器_伏城之外的博客-CSDN博客 CSS Selectors Reference...

【初阶数据结构】二叉树全面知识总结
二叉树详解 树的概念及其结构树的概念树的相关概念树的表示方法孩纸兄弟表示法双亲表示法(并查集) 树的实际应用 二叉树二叉树的概念二叉树的种类二叉树的性质二叉树的存储结构 二叉树顺序结构的实现堆的概念及结构堆向上、向下调整法堆的插入堆的删除堆…...
CMD命令终端快捷键学习
很多环境需要安装并且指定环境变量才可用终端访问 比如一些数据库、一些环境、例如:nodejs Oracle、mysql 在一个文件夹按住shift鼠标右键可以快速在当前目录运行终端!免去cd 目录的烦恼 快捷键 当你学习和使用命令终端(如 Windows 的 CMD&…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
