【算法分析与设计】算法概述
目录
- 一、学习要点
- 二、算法的定义
- 三、算法的性质
- 四、程序(Program)
- 五、问题求解(Problem Solving)
- 六、算法的描述
- 七、算法分析的目的
- 八、算法复杂性分析
- (一)算法时间复杂性分析
- (二)算法渐近复杂性
- 1、渐进上界记号-大O符号
- 2、渐进下界记号-大Ω符号
- 3、紧渐进界记号-Θ符号
- 4、非紧上界记号o
- 5、非紧下界记号ω
- 6、渐近分析记号在等式和不等式中的意义
- 7、渐近分析中函数比较
- 8、渐近分析记号的若干性质
- (1)传递性
- (2)反身性
- (3)对称性
- (4)互对称性
- (5)算术运算
- 9、算法渐近复杂性分析中常用函数
- (1)单调函数
- (2)取整函数
- 取整函数的若干性质
- (3)多项式函数
- (4)指数函数
- (5)对数函数
- (6)阶乘函数
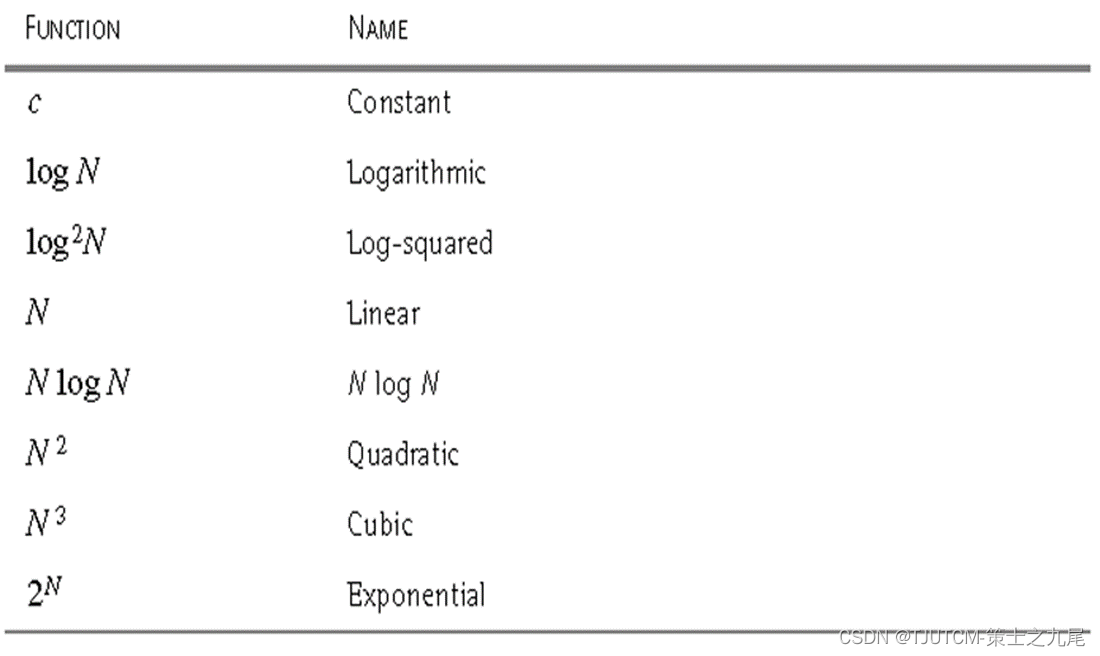
- 10、算法分析中常见的复杂性函数
- (1)小规模数据
- (2)中等规模数据
- (3)算法分析方法
- 九、算法分析的基本法则
- 1、非递归算法:
- (1)for / while 循环
- (2)嵌套循环
- (3)顺序语句
- (4)if-else语句
- 2、最优算法
数据结构+算法(+设计模式)=程序
一、学习要点
理解算法的概念。
掌握算法的计算复杂性概念。
掌握算法复杂性的渐近性态的数学表述。
了解NP类问题的基本概念。
二、算法的定义
顾名思义,计算(求解)的方法
算法(Algorithm):对特定问题求解步骤的一种描述,是指令的有限序列。
算法是指解决问题的一种方法或一个过程。
程序设计=数据结构+算法(+设计模式)
三、算法的性质
算法是若干指令的有穷序列,满足性质:
(1)输入:有外部提供的量作为算法的输入。
(2)输出:算法产生至少一个量作为输出。
(3)确定性:组成算法的每条指令是清晰,无歧义的。
(4)有限性:算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
四、程序(Program)
程序是算法用某种程序设计语言的具体实现。
程序可以不满足算法的性质。
例如操作系统,是一个在无限循环中执行的程序,因而不是一个算法。
操作系统的各种任务可看成是单独的问题,每一个问题由操作系统中的一个子程序通过特定的算法来实现。该子程序得到输出结果后便终止。
五、问题求解(Problem Solving)
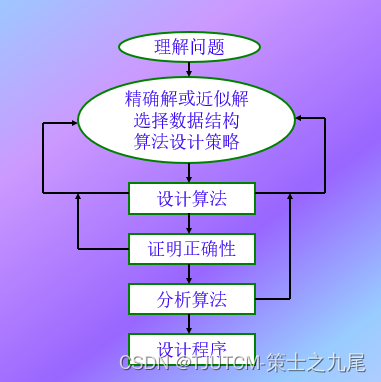
六、算法的描述
自然语言或表格
伪码方式
C++语言
Java语言
C语言
Python等其他语言
七、算法分析的目的
对算法所需要的两种计算机资源——时间和空间进行估算
设计算法——设计出复杂性尽可能低的算法
选择算法——在多种算法中选择其中复杂性最低者
八、算法复杂性分析
算法复杂性是算法运行所需要的计算机资源的量,
需要时间资源的量称为时间复杂性,需要的空间资源的量称为空间复杂性。
这个量应该只依赖于算法要解的问题的规模、算法的输入和算法本身的函数。
如果分别用N、I和A表示算法要解问题的规模、算法的输入和算法本身,而且用C表示复杂性,那么,应该有C=F(N,I,A)。
一般把时间复杂性和空间复杂性分开,并分别用T和S来表示,则有: T=T(N,I)和S=S(N,I)(通常,让A隐含在复杂性函数名当中)
(一)算法时间复杂性分析
最坏情况下的时间复杂性:
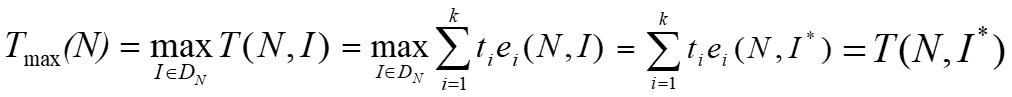
最好情况下的时间复杂性:
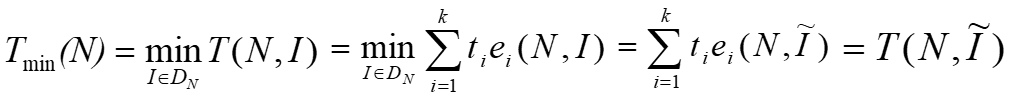
平均情况下的时间复杂性:
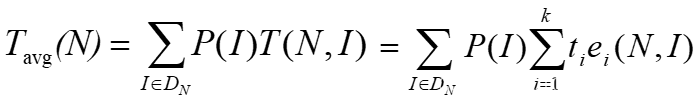
其中DN是规模为N的合法输入的集合;I* 是DN中使T(N, I*)达到Tmax(N)的合法输入; 是中使T(N, I*)达到Tmin(N)的合法输入;而P(I)是在算法的应用中出现输入I的概率。
(二)算法渐近复杂性
T(n) →∞ , 当 n→∞ ;
(T(n) - t(n) )/ T(n) →0 ,当 n→∞;
t(n)是T(n)的渐近性态,为算法的渐近复杂性。
在数学上, t(n)是T(n)的渐近表达式,是T(n)略去低阶项留下的主项。它比T(n) 简单。
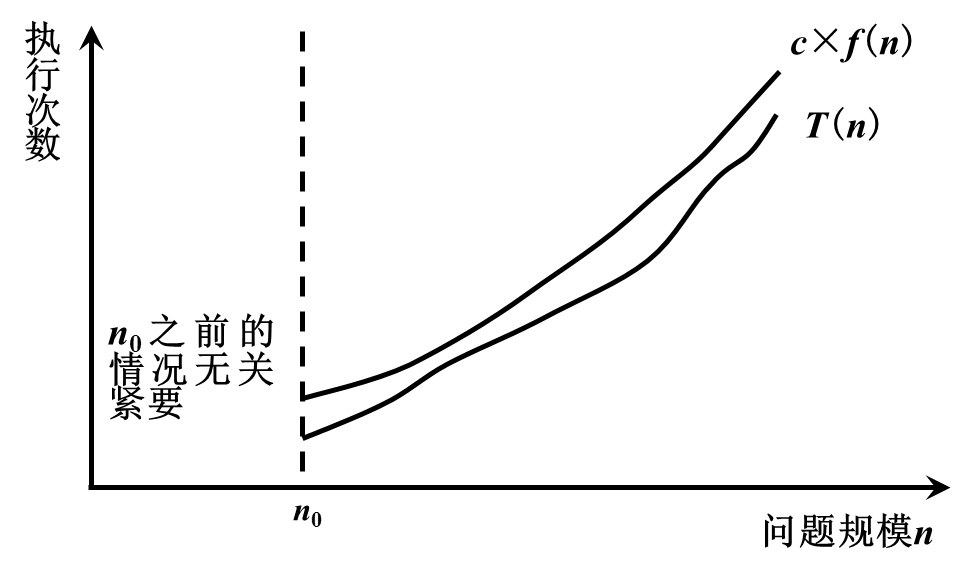
1、渐进上界记号-大O符号
若存在两个正的常数c和n0,对于任意n≥n0,都有T(n)≤c×f(n),则称T(n)=O(f(n))
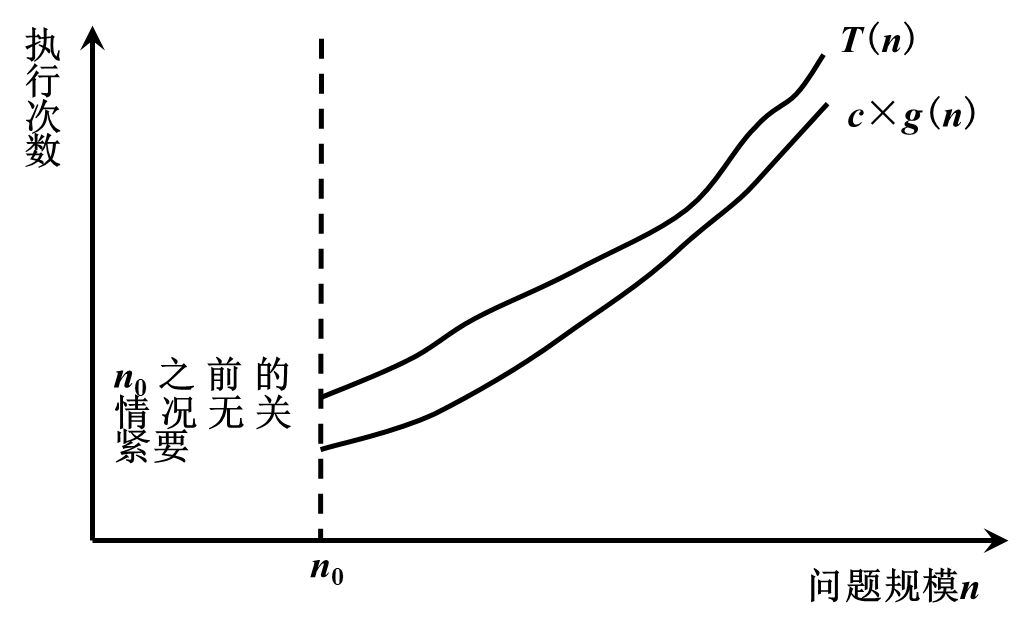
2、渐进下界记号-大Ω符号
若存在两个正的常数c和n0,对于任意n≥n0,都有T(n)≥c×g(n),则称T(n)=Ω(g(n))
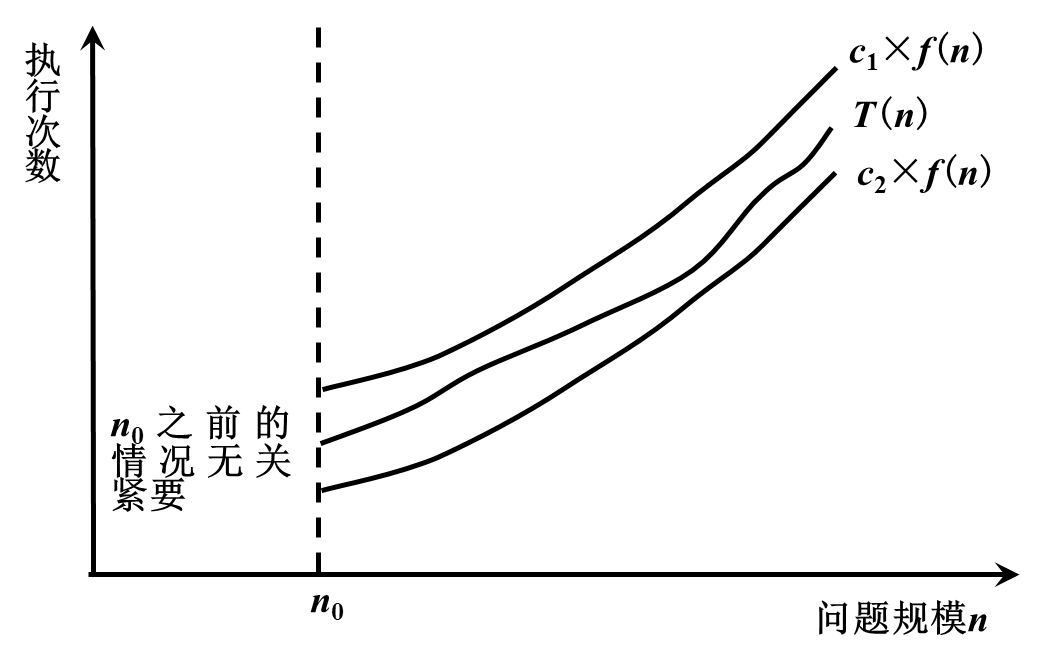
3、紧渐进界记号-Θ符号
若存在三个正的常数c1、c2和n0,对于任意n≥n0都有c1×f(n)≥T(n)≥c2×f(n),则称T(n)=Θ(f(n))
例: T(n)=5n2+8n+1
当n≥1时,5n2+8n+1≤5n2+8n+n=5n2+9n≤5n2+9n2≤14n2=O(n2)
当n≥1时,5n2+8n+1≥5n2=Ω(n2)
∴ 当n≥1时,14n2≥5n2+8n+1≥5n2
则:5n2+8n+1=Θ(n2)
定理:若T(n)=amnm +am-1nm-1 + … +a1n+a0(am>0),则有T(n)=O(nm)且T(n)=Ω(n m),因此,有T(n)=Θ(n m)。
4、非紧上界记号o
o(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0<f(n)<cg(n) }
等价于 f(n) / g(n) →0 ,当 n→∞。
5、非紧下界记号ω
ω(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n> n0有:0 ≤ cg(n) < f(n) }
等价于 f(n) / g(n) →∞ ,当 n→∞。
6、渐近分析记号在等式和不等式中的意义
f(n)= Θ(g(n))的确切意义是:f(n) ∈ Θ(g(n))。
一般情况下,等式和不等式中的渐近记号Θ(g(n))表示Θ(g(n))中的某个函数。
例如:2n2 + 3n + 1 = 2n2 + Θ(n) 表示
2n2 +3n +1=2n2 + f(n),其中f(n) 是Θ(n)中某个函数。
等式和不等式中渐近记号O,o, Ω和ω的意义是类似的。
7、渐近分析中函数比较
f(n)= O(g(n)) ≈ a ≤ b;
f(n)= Ω(g(n)) ≈ a ≥ b;
f(n)= Θ(g(n)) ≈ a = b;
f(n)= o(g(n)) ≈ a < b;
f(n)= ω(g(n)) ≈ a > b.
8、渐近分析记号的若干性质
(1)传递性
f(n)= Θ(g(n)), g(n)= Θ(h(n)) → f(n)= Θ(h(n));
f(n)= O(g(n)), g(n)= O (h(n)) → f(n)= O (h(n));
f(n)= Ω(g(n)), g(n)= Ω (h(n)) → f(n)= Ω(h(n));
f(n)= o(g(n)), g(n)= o(h(n)) → f(n)= o(h(n));
f(n)= ω(g(n)), g(n)= ω(h(n)) → f(n)= ω(h(n));
(2)反身性
f(n)= Θ(f(n));
f(n)= O(f(n));
f(n)= ω(f(n)).
(3)对称性
f(n)= Θ(g(n)) ⇔ g(n)= Θ (f(n)) .
(4)互对称性
f(n)= O(g(n)) ⇔ g(n)= Ω (f(n)) ;
f(n)= o(g(n)) ⇔ g(n)= ω (f(n)) ;
(5)算术运算
O(f(n))+O(g(n)) = O(max{f(n),g(n)}) ;
O(f(n))+O(g(n)) = O(f(n)+g(n)) ;
O(f(n))*O(g(n)) = O(f(n)*g(n)) ;
O(cf(n)) = O(f(n)) ;
g(n)= O(f(n)) → O(f(n))+O(g(n)) = O(f(n)) 。
规则O(f(n))+O(g(n)) = O(max{f(n),g(n)}) 的证明:
对于任意f1(n) ∈ O(f(n)) ,存在正常数c1和自然数n1,使得对所有n≥ n1,有f1(n) ≤ c1f(n) 。
类似地,对于任意g1(n) ∈ O(g(n)) ,存在正常数c2和自然数n2,使得对所有n≥ n2,有g1(n) ≤ c2g(n) 。
令c3=max{c1, c2}, n3 =max{n1, n2},h(n)= max{f(n),g(n)} 。
则对所有的 n ≥ n3,有
f1(n) +g1(n) ≤ c1f(n) + c2g(n)
≤ c3f(n) + c3g(n)= c3(f(n) + g(n))
≤ c32 max{f(n),g(n)}
= 2c3h(n) = O(max{f(n),g(n)}) .
9、算法渐近复杂性分析中常用函数
(1)单调函数
单调递增:m ≤ n → f(m) ≤ f(n) ;
单调递减:m ≥ n → f(m) ≥ f(n);
严格单调递增:m < n → f(m) < f(n);
严格单调递减:m > n → f(m) > f(n).
(2)取整函数
⌊ x ⌋ :不大于x的最大整数;
⌈ x ⌉ :不小于x的最小整数。
取整函数的若干性质
x-1 < ⌊ x ⌋ ≤ x ≤ ⌈ x ⌉ < x+1;
⌊ n/2 ⌋ + ⌈ n/2 ⌉ = 整数n;
对于n ≥ 0,a,b>0,有:
⌈ ⌈ n/a ⌉ /b ⌉ = ⌈ n/ab ⌉ ;
⌊ ⌊ n/a ⌋ /b ⌋ = ⌊ n/ab ⌋ ;
⌈ a/b ⌉ ≤ (a+(b-1))/b;
⌊ a/b ⌋ ≥ (a-(b-1))/b;
f(x)= ⌊ x ⌋ , g(x)= ⌈ x ⌉ 为单调递增函数。
(3)多项式函数
p(n)= a0+a1n+a2n2+…+adnd; ad>0;
p(n) = Θ(nd);
f(n) = O(nk) ⇔ f(n)多项式有界;
f(n) = O(1) ⇔ f(n) ≤ c;
k ≥ d → p(n) = O(nk) ;
k ≤ d → p(n) = Ω(nk) ;
k > d → p(n) = o(nk) ;
k < d → p(n) = ω(nk) .
(4)指数函数
对于正整数m,n和实数a>0:
a0=1;
a1=a ;
a-1=1/a ;
(am)n = amn ;
(am)n = (an)m ;
aman = am+n ;
a>1 → an为单调递增函数;
a>1 →
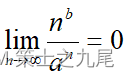
→ nb = o(an)
(5)对数函数
log n = log2n;
lg n = log10n;
ln n = logen;
logkn = (log n)k;
log log n = log(log n);
for a>0,b>0,c>0

(6)阶乘函数
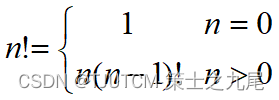
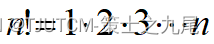
Stirling’s approximation
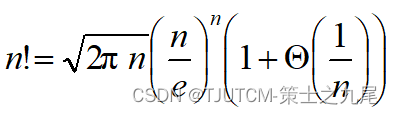
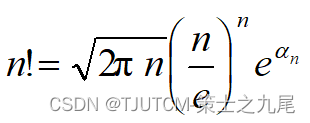

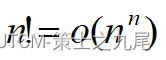
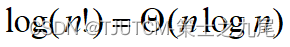
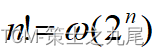
10、算法分析中常见的复杂性函数
(1)小规模数据
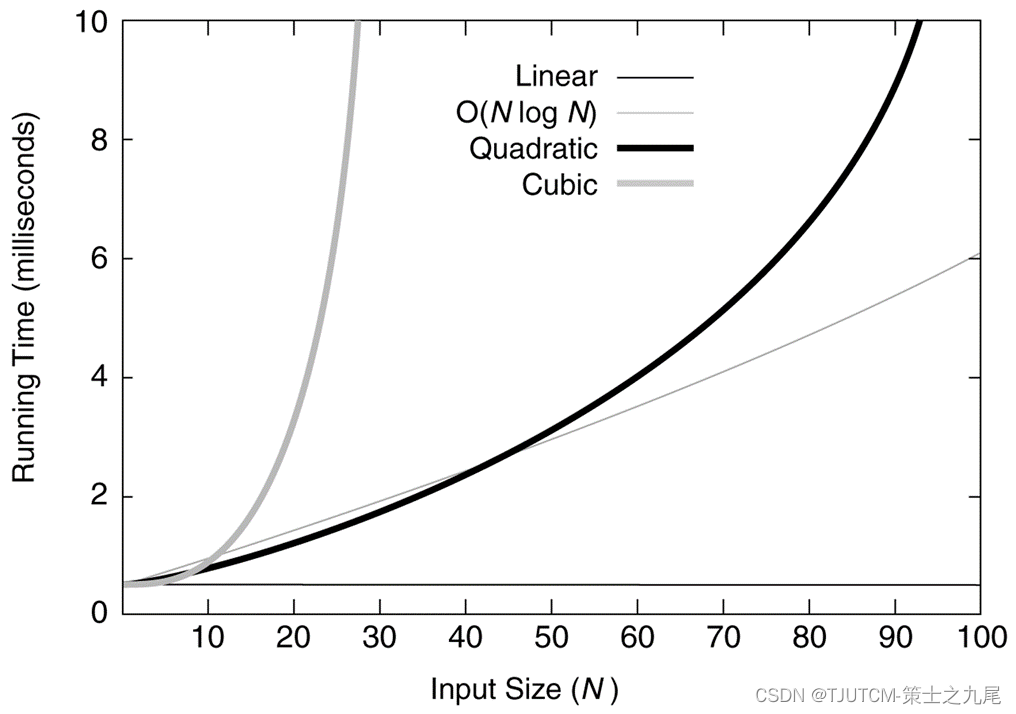
(2)中等规模数据
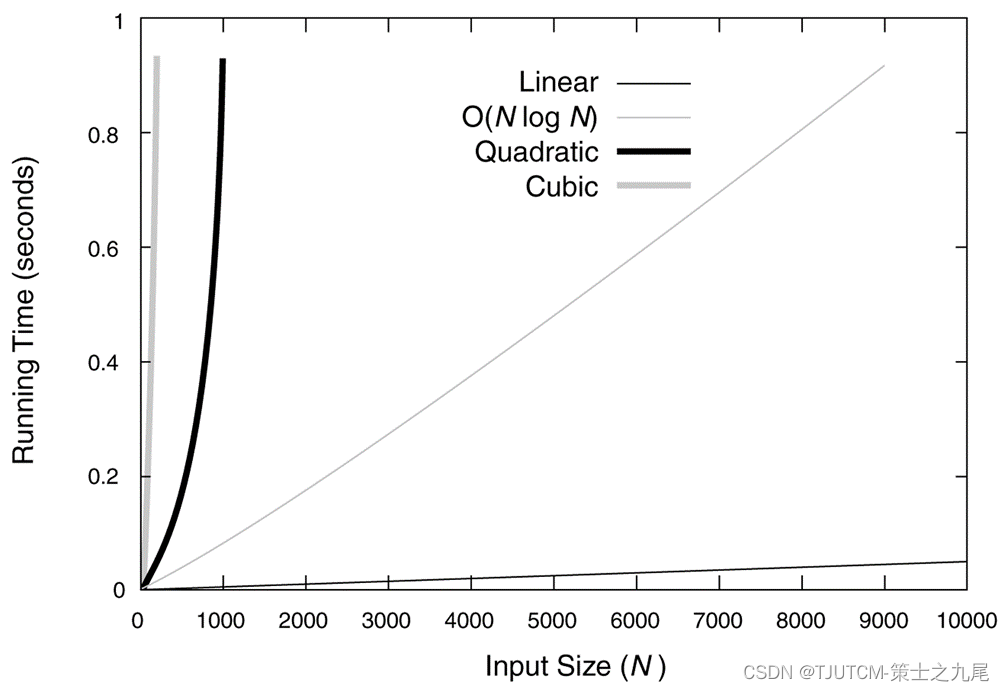
(3)算法分析方法
例:顺序搜索算法
template<class Type>
int seqSearch(Type *a, int n, Type k)
{for(int i=0;i<n;i++)if (a[i]==k) return i;return -1;
}
(1)Tmax(n) = max{ T(I) | size(I)=n }=O(n)
(2)Tmin(n) = min { T(I) | size(I)=n }=O(1)
(3)在平均情况下,假设:
(a) 搜索成功的概率为p ( 0 ≤ p ≤ 1 );
(b) 在数组的每个位置i ( 0 ≤ i < n )搜索成功的概率相同,均为 p/n。
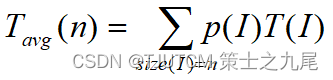
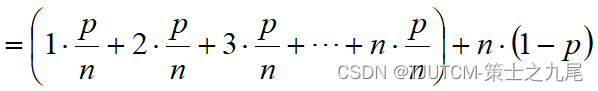
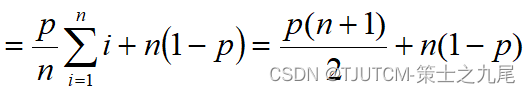
九、算法分析的基本法则
1、非递归算法:
(1)for / while 循环
循环体内计算时间*循环次数;
(2)嵌套循环
循环体内计算时间*所有循环次数;
(3)顺序语句
各语句计算时间相加;
(4)if-else语句
if语句计算时间和else语句计算时间的较大者。
2、最优算法
问题的计算时间下界为Ω(f(n)),则计算时间复杂性为O(f(n))的算法是最优算法。
例如,排序问题的计算时间下界为Ω(nlogn),计算时间复杂性为O(nlogn)的排序算法是最优算法。
堆排序算法是最优算法。
相关文章:
【算法分析与设计】算法概述
目录 一、学习要点二、算法的定义三、算法的性质四、程序(Program)五、问题求解(Problem Solving)六、算法的描述七、算法分析的目的八、算法复杂性分析(一)算法时间复杂性分析(二)算法渐近复杂性1、渐进上界记号-大O符号2、渐进下…...
如何进一步全面提高项目估算精准度?
项目估算非常重要,这直接关系着项目的成本和收入,如果估算不准确,将为项目带来较大风险。一般软件规模可以用多种方式进行估算,但是用功能点估算方式更准确,而自动估算让估算更快速,我们以CoCode开发的估算…...
Git学习笔记4
GitHub是目前最火的开源项目代码托管平台。它是基于web的Git仓库,提供公有仓库和私有仓库,但私有仓库是需要付费的。 到Github上找类似的项目软件。 GitLab可以创建免费的私有仓库。 GitLab是利用 Ruby开发的一个开源的版本管理系统,实现一个…...

【红外与可见光图像融合】离散平稳小波变换域中基于离散余弦变换和局部空间频率的红外与视觉图像融合方法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

成都睿趣科技:抖音开通橱窗带货需要钱吗
随着社交媒体和电子商务的蓬勃发展,抖音作为一种流行的短视频平台,也推出了自己的“抖音橱窗”功能,让内容创作者能够通过视频展示和销售产品,从而实现商业化。那么,抖音橱窗带货是否需要费用呢? 首先,要开…...
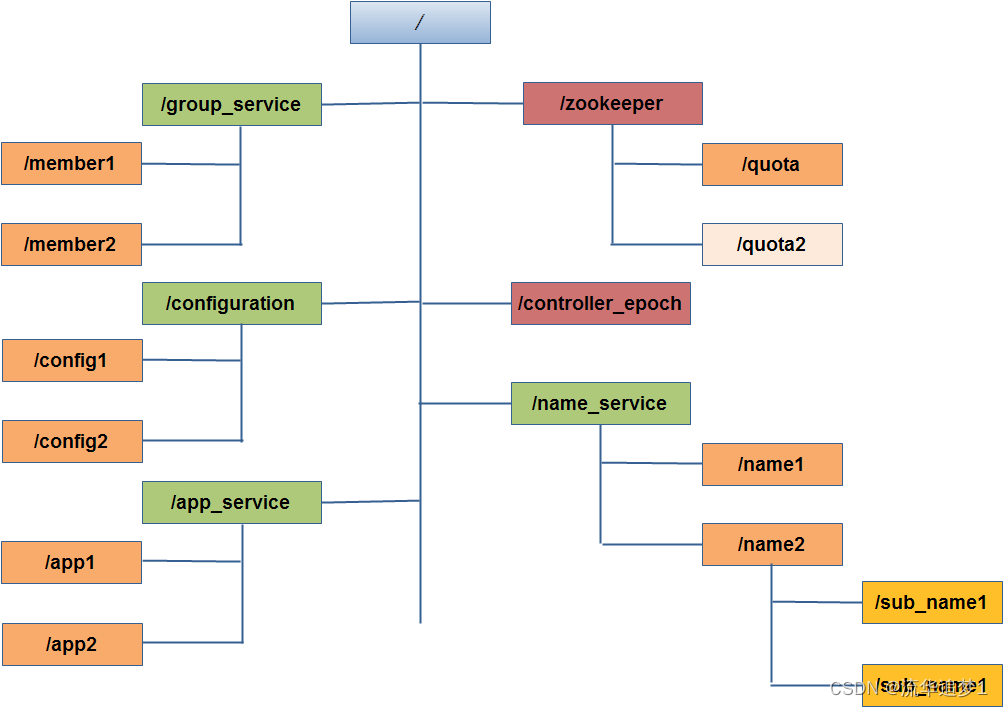
中间件 - 分布式协调服务Zookeeper
目录 一. 前言 二. 树状结构 2.1. ZNode 2.1.1. stat 2.1.2. ACL 三. NameService命名服务 四. Configuration 配置管理 五. GroupMembers 集群管理 六. 集群三个角色及状态 七. 选举算法 八. Watcher 九. 设计目的 十. 典型使用场景 一. 前言 Zookeeper是一个分布…...

golang的实用工具
golang的实用工具 Go 语言提供了许多实用的工具,以下是其中一些常用的工具: 1. go run:用于直接运行 Go 源代码文件,无需显式编译。 2. go build:用于将 Go 代码编译成可执行文件或库。 3. go test:用于…...
)
图层混合模式(三)
差值模式 差值模式:查看每个通道的数值,用基色减去混合色或用混合色减去基色。具体取决于混合色与基色那个通道的数值更大。白色与任何颜色混合得到反相色,黑色与任何颜色混合颜色不变。 计算公式:结果色 绝对值(混合…...
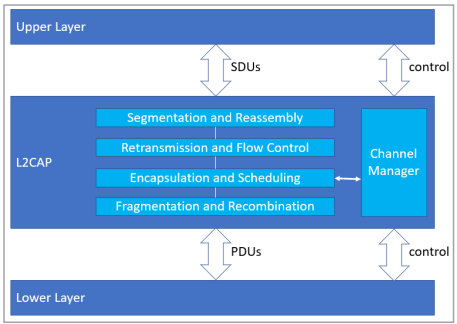
蓝牙核心规范(V5.4)10.6-BLE 入门笔记之L2CAP
蓝牙篇之蓝牙核心规范(V5.4)深入详解汇总 1.概述 L2CAP负责协议复用、流量控制、服务数据单元(SDU)的分段和重组。它使用通道的概念来分隔在堆栈层之间传递的数据包序列。固定通道不需要设置,立即可用,并与特定的上层协议相关联。通道也可以通过指定的协议服务多路复用器…...

【计算机网络】DNS原理介绍
文章目录 DNS提供的服务DNS的工作机理DNS查询过程DNS缓存 DNS记录和报文DNS记录DNS报文针对DNS服务的攻击 DNS提供的服务 DNS,即域名系统(Domain Name System) 提供的服务 一种实现从主机名到IP地址转换的目录服务,为Internet上的用户应用程序以及其他…...

Docker的基础命令
目录 一、镜像操作 1、搜索镜像 2、下载镜像 3、查看镜像 3.1 查看下载到本地的所有镜像 3.2 查看单个镜像的详细信息 4、为镜像添加新的标签 5、镜像导出和导入到本地 5.1 镜像导出到本地 5.2 导入镜像 6、删除镜像 7、批量删除镜像 8、上传镜像 8.1 官网注册登录…...

提取项目依赖包的licenses
skywalking-eyes工具可以快速提取出licenses...

Vue项目自动转换px为rem-高保真还原设计图
前端开发中还原设计图的重要性毋庸置疑,目前来说应用最多的应该也还是使用rem。然而很多人依然还是处于刀耕火种的时代,要么自己去计算rem值,要么依靠编辑器安装插件转换。 而本文的目标就是通过一系列的配置后,在开发中可以直接使…...

rman备份到远程服务器
rman备份到远程服务器磁盘 原因 业务数据量较大,数据库服务器上无足够地空间存放rman备份,磁盘扩容申请不批。无奈采取nfs远程备份 环境信息 ip操作系统备份目录远程备份服务器192.168.3.130Centos7.9rmanbak数据库服务器192.168.3.132:1521Centos7.…...
数据结构与算法
目录 数据结构与算法 为什么要学习数据结构和算法? 常见的数据结构 常用算法 插入排序 一、概念及其介绍 二、适用说明 三、过程图示 希尔排序 一、概念及其介绍 二、适用说明 三、过程图示 归并排序 一、概念及其介绍 二、适用说明 三、过程图示 …...
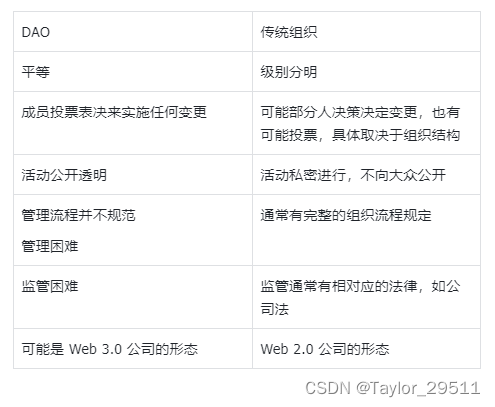
【Web3】DAO相关的基础知识
这里写目录标题 DAO 的基础概念为什么需要 DAO?DAO 的种类 DAO 的运作方式知名 DAO 的介绍Bankless DAOSeeDAO DAO 的生态全景图分类治理框架DAO 的工具 DAO 众筹平台介绍 - JuiceBoxDAO 投票治理介绍 - SnapshotDAO 贡献 & 激励 - POAPDAO 信息管理 - NotionDA…...

一文教你学会ArcGIS Pro地图设计与制图系列全流程(3)
ArcGIS Pro做的成果图及系列文章目录: 系列文章全集: 《一文教你学会ArcGIS Pro地图设计与制图系列全流程(1)》《一文教你学会ArcGIS Pro地图设计与制图系列全流程(2)》《一文教你学会ArcGIS Pro地图设计与…...
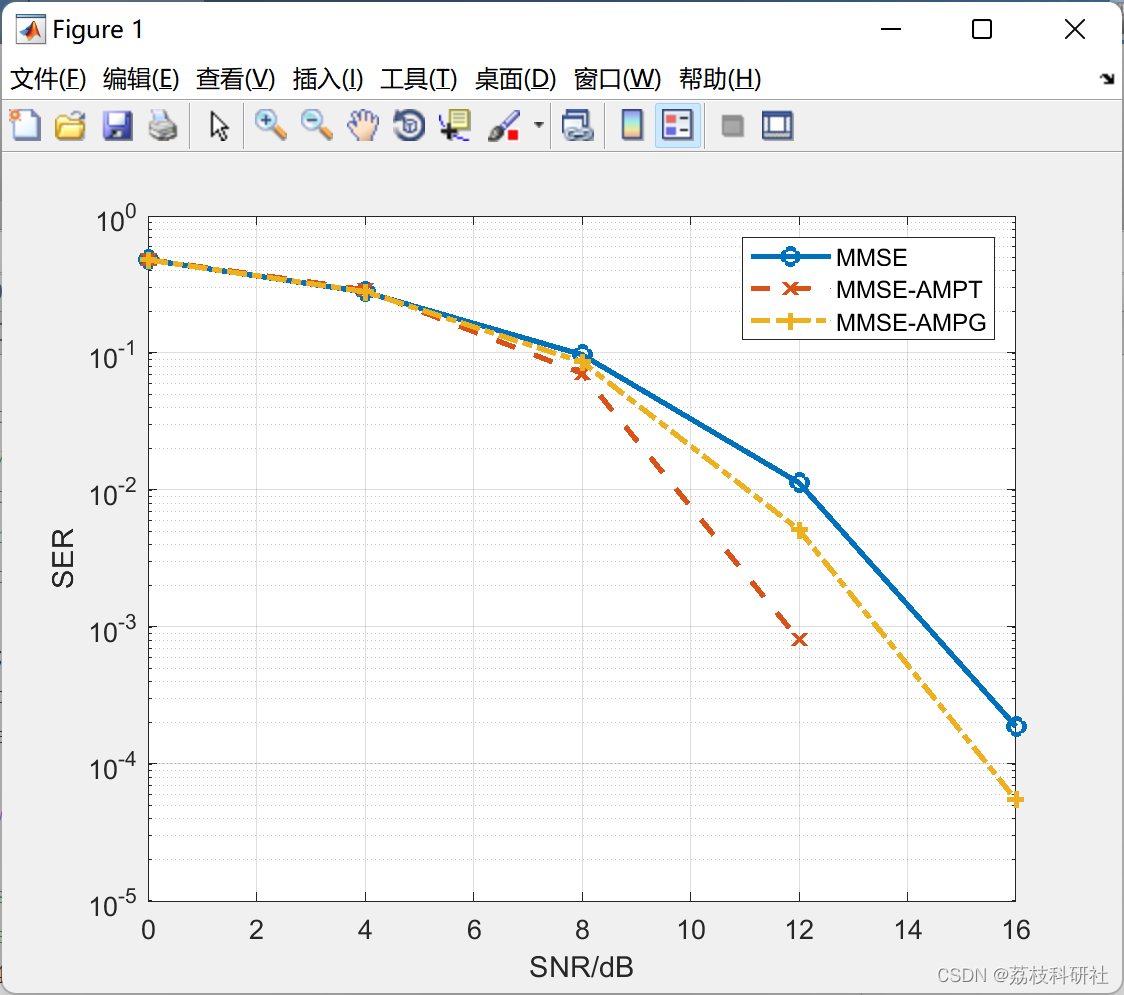
用于大规模 MIMO 检测的近似消息传递 (AMP)(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
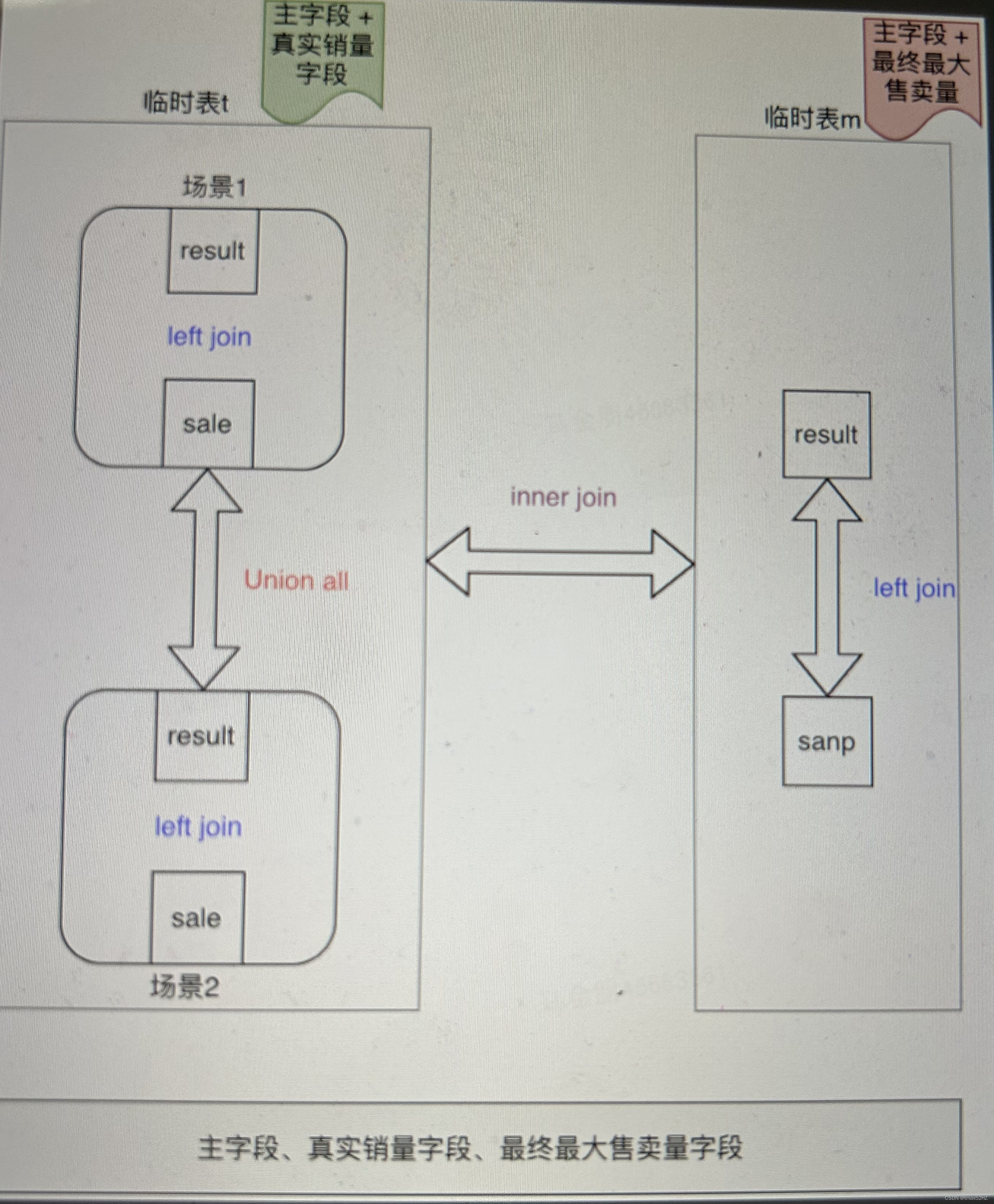
复杂SQL解析
文章目录 背景表SQL关键字分析具体Sql注意点补充:select的字段,也可以带有计算逻辑 背景表 1、sale_log as result: 主表,大部分字段都是取自这个表 2、sale_num as sale:需要从这个表获取真实销量sale_num字段 3、schedule as…...

js中哪些地方会用到window?
前言 Window 对象是JavaScript中的顶层对象,它代表了浏览器中打开的窗口或者标签页。浏览器中打开的每一个窗口/标签页都会有一个对应的 Window 对象。在浏览器中,全局作用域的 this 就是指向 Window 对象。 正文 在 JavaScript 中,window 对…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
