leetcode面试经典150题第一弹(一)
leetcode面试经典150题第一弹
一、合并俩个有序数组(难度:简单)
题目
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按非递减顺序排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
解题思路
直接合并后排序,最直观的方法是先将数组nums2放进数组nums1的尾部,然后直接对整个数组进行排序。
1、splice直接改变原数组,可用于删除、插入、替换
2、使用sort进行排序:
sort((a, b) => a - b)为正序,即从小到到大
sort((a, b) => a - b)为倒叙,即从大到小
代码示例
/*** @param {number[]} nums1* @param {number} m* @param {number[]} nums2* @param {number} n* @return {void} Do not return anything, modify nums1 in-place instead.*/
var merge = function(nums1, m, nums2, n) {nums1.splice(m, nums1.length - m, ...nums2);nums1.sort((a, b) => a - b);
};
结果
二、移除元素(难度:简单)
题目
给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
解题思路
1、js中splice可以直接改变原数组,直接使用splice删除
2、在ES6中有更简单直接的方法去重,Array.from(new Set(arr)),但是这样会改变原数组,导致leetCode测试用例不通过。题目中要求原地修改数组
代码示例
/*** @param {number[]} nums* @param {number} val* @return {number}*/
var removeElement = function(nums, val) {for(let i = 0; i < nums.length; i++) {if(nums[i] === val) {nums.splice(i, 1)i--}}
};结果
三、删除有序数组中的重复项(难度:简单)
题目
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
解题思路
我在这道题的解题中使用了ES6中的new Map(),利用map每个键都是唯一的特性去重
1、ES6中map,是一种有序的键值对集合,其中每个键都是唯一的。它可以存储任何类型的值作为键或值,包括原始类型和对象引用。
2、map.set("name","xiaobaigis"),添加键值对
3、map.has(5),判断是否有指定键
代码示例
/*** @param {number[]} nums* @return {number}*/
var removeDuplicates = function(nums) {let newMap = new Map()for(let i = nums.length; i >= 0; i-- ) {if(newMap.has(nums[i])) {nums.splice(i, 1)} else {newMap.set(nums[i])}}
};
结果

四、删除有序数组中的重复项(难度:中等)
题目
给你一个有序数组 nums ,请你原地删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组 并在使用O(1) 额外空间的条件下完成。
解题思路
1、因为是个有序数组,所以如果相同的元素必定在一起,判断如果有三个相邻元素相同,则删掉一个元素
2、splice直接改变原数组,可用于删除、插入、替换
代码示例
/*** @param {number[]} nums* @return {number}*/
var removeDuplicates = function(nums) {if(nums.length < 3) {return;}for(let i = 2; i < nums.length; i++) {if(nums[i] === nums[i-1] && nums[i] === nums[i-2]) {nums.splice(i, 1)i--}}
};
结果
欢迎关注我的个人公众号:javascript艺术
相关文章:

leetcode面试经典150题第一弹(一)
leetcode面试经典150题第一弹 一、合并俩个有序数组(难度:简单) 题目 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并…...

VME-7807RC-414001 350-93007807-414001 VMIVME-017807-411001 VMIVME-017807-414001
VME-7807RC-414001 350-93007807-414001 VMIVME-017807-411001 VMIVME-017807-414001 由于第12代英特尔酷睿处理器的16核/24线程配置,Nuvo-9000型号与之前的平台相比,性能大幅提升。它们还支持新的DDR5内存标准,以获得更多内存带宽…...

01-Zookeeper特性与节点数据类型详解
上一篇: 在了解Zookeeper之前,需要对分布式相关知识有一定了解,什么是分布式系统呢?通常情况下,单个物理节点很容易达到性能,计算或者容量的瓶颈,所以这个时候就需要多个物理节点来共同完成某项…...

TP6 TP8 使用阿里官方OSS SDK方法
安装 composer require aliyuncs/oss-sdk-php 官网:GitHub - aliyun/aliyun-oss-php-sdk: Aliyun OSS SDK for PHP 二、PHP简单上传 官网教程:如何进行字符串上传和文件上传_对象存储 OSS-阿里云帮助中心 引入 use OSS\OssClient; use OSS\Core\OssE…...
SkyWalking分布式链路追踪学习
为什么要用分布式链路追踪 实际生产中,面对几十个、甚至成百上千个的微服务实例,如果一旦某个实例发生宕机,如果不能快速定位、提交预警,对实际生产造成的损失无疑是巨大的。所以,要对微服务进行监控、预警࿰…...

git revert 撤销之前的提交
git revert 用来撤销之前的提交,它会生成一个新的 commit id 。 输入 git revert --help 可以看到帮忙信息。 git revert commitID 不编辑新的 commit 说明 git log 找到需要撤销的 commitID , 然后执行 git revert commitID ,会提示如下…...
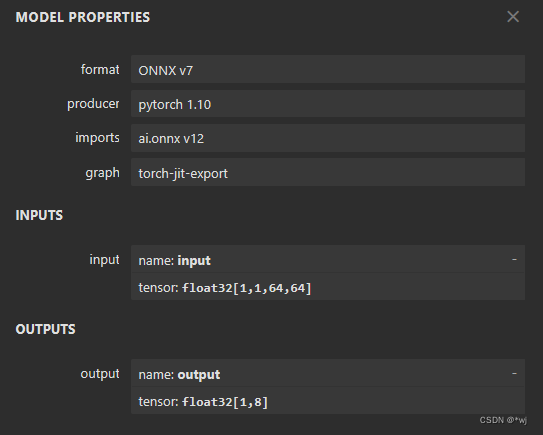
rk3568环境配置和推理报错: RKNN_ERR_MALLOC_FAIL
前言 最近在部署算法在板子侧遇到的一些问题汇总一下: 一、版本问题 经过测试现在将自己环境配置如下: 本地linux安装rknn-toolkit2-1.5.0 本地Linux使用的miniconda新建的一个python虚拟环境(自行网上查找相关方法) 安装好自…...
)
网络工程师基础笔记(一)
一、接入网 接入网,是指将端系统物理连接到边缘路由器的网络。 (1)家庭接入:数字用户线(DSL)、电缆、光纤到户(FTTH)卫星和拨号接入。 (2)企业(家庭)接入&…...
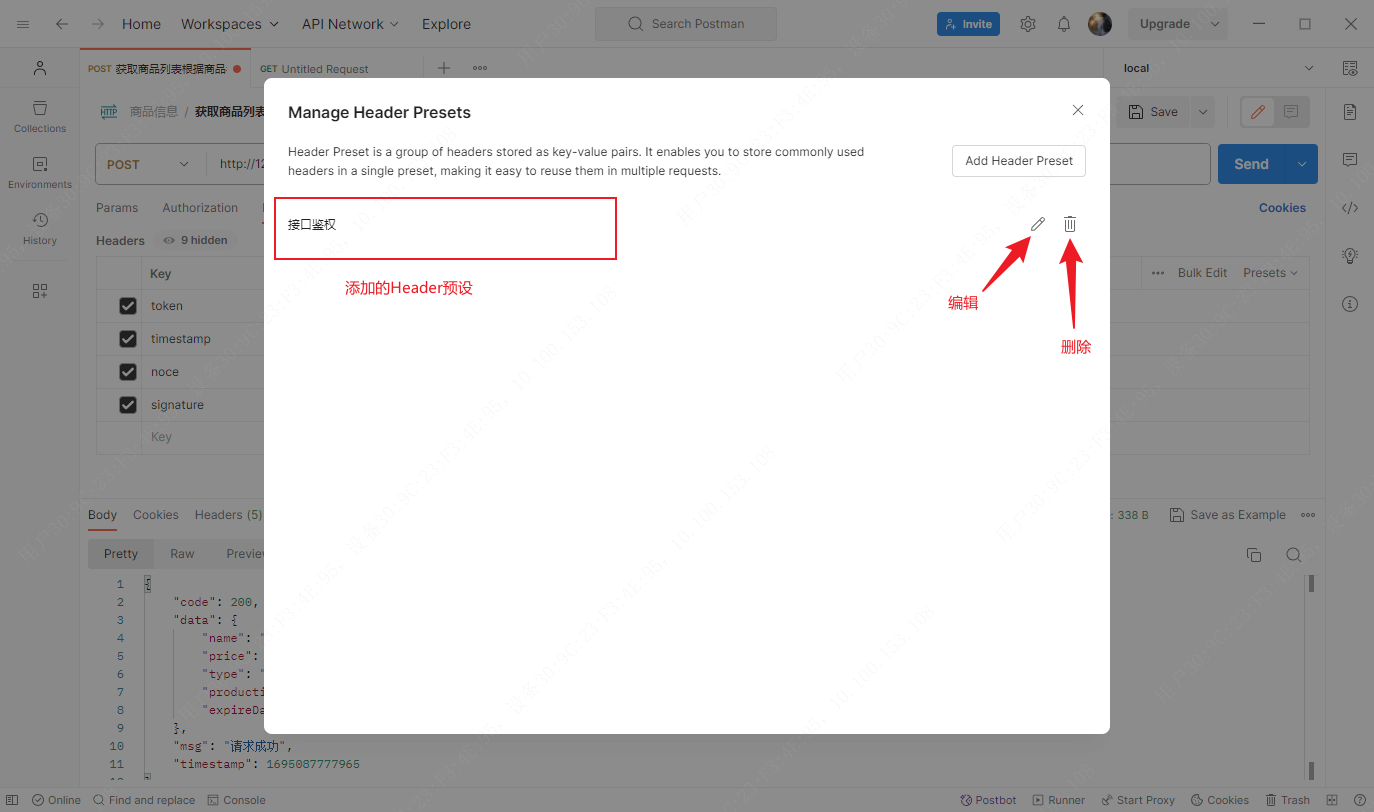
Postman应用——Headers请求头设置
文章目录 Header设置Header删除或禁用Header批量编辑Header预设添加 一般在接口需要校验签名时,Headers请求头用来携带签名和生成签名需要的参数,在Postman也可以设置请求头在接口请求时携带参数。 Header设置 说明: Key:Header…...
人人都是项目经理-项目管理概述(一)
一、重新认识项目管理 1. 什么是项目 项目(Project),是为提供某项独特的产品(交付物),服务或成果所做的临时性努力。 – PMBOK指南 项目是指一系列独特的、复杂的并相互关联的活动,这些活动有着…...

浅谈基于物联网的医院消防安全管理
安科瑞 华楠 摘 要:医院消防物联网将原本与网络无关的消防设施和网络结合起来,将消防监督管理、防火灭火所需的相关信息进行汇总,可以让医院更加轻松地发现和处理医院的警情信息,降低火灾发生频率。 关键词:物联网技…...

户用储能争斗:华宝新能“稳”、正浩科技“快”、安克创新“急”
便携式储能市场一片红海,户用储能(家用储能)成为储能企业新的“格斗场”。 过去两年,房车游、户外旅行、露营等旅游项目热度攀升,户外用电需求与日俱增,嗅觉敏锐的资本方相继加码便携储能市场,越…...

【面试篇】集合相关高频面试题
目录 1. ArrayList和LinkedList的区别?2. HashMap和HashTable的区别?1. ArrayList和LinkedList的区别? ArrayListLinkedList数据结构数组链表插入和删除在中间插入或删除元素时需要移动数组中的其他元素,时间复杂度为O(n)只需要调整指针,时间复杂度为O(1)访问元素通过索引…...

RT Preempt linux学习笔记
RT Preempt linux学习笔记 一、实时操作系统(Realtime Operating System) 1. 什么是实时操作系统 A real-time system is a time-bound system which has well-defined, fixed time constraints. Processing must be done within the defined constra…...
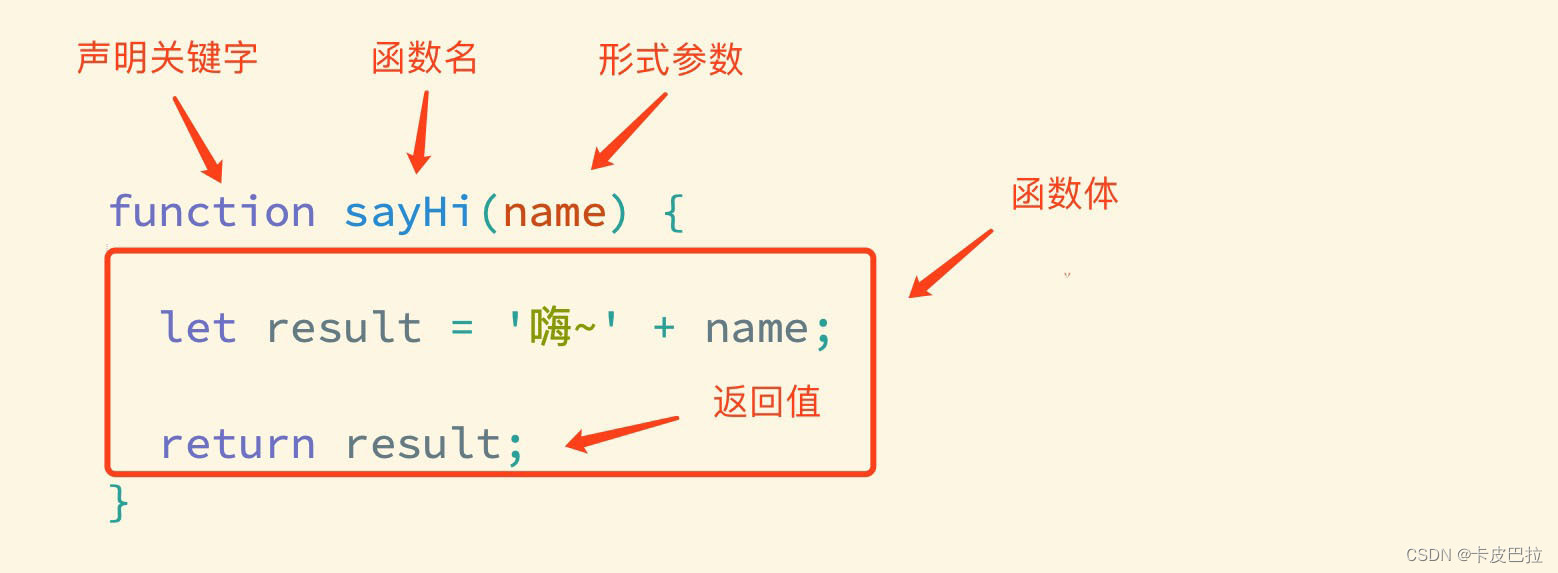
JavaScript 基础第四天笔记
JavaScript 基础 - 第4天笔记 理解封装的意义,能够通过函数的声明实现逻辑的封装,知道对象数据类型的特征,结合数学对象实现简单计算功能。 理解函数的封装的特征掌握函数声明的语法理解什么是函数的返回值知道并能使用常见的内置函数 函数 …...

Unity 2021.x及以下全版本Crack
前言 最近Unity那档子事不出来了吗,搞得所有人都挺烦的,顺便在公司内网需要我完成一个游戏的项目,就研究了一下如何将Unity给Crack掉。 注意所有操作应有连接外网的权限 以我选择的版本为例,我使用的是Unity 2021.3.5f1与Unity…...

基于知识蒸馏的夜间低照度图像增强及目标检测
源自:应用光学 作者:苗德邻, 刘磊, 莫涌超, 胡朝龙, 张益军, 钱芸生. “人工智能技术与咨询” 发布 摘要 为了实现夜间低照度图像的增强,提高目标检测模型在夜间低照度条件下的检测精度并减小模型的计算成本,提出了一种基…...
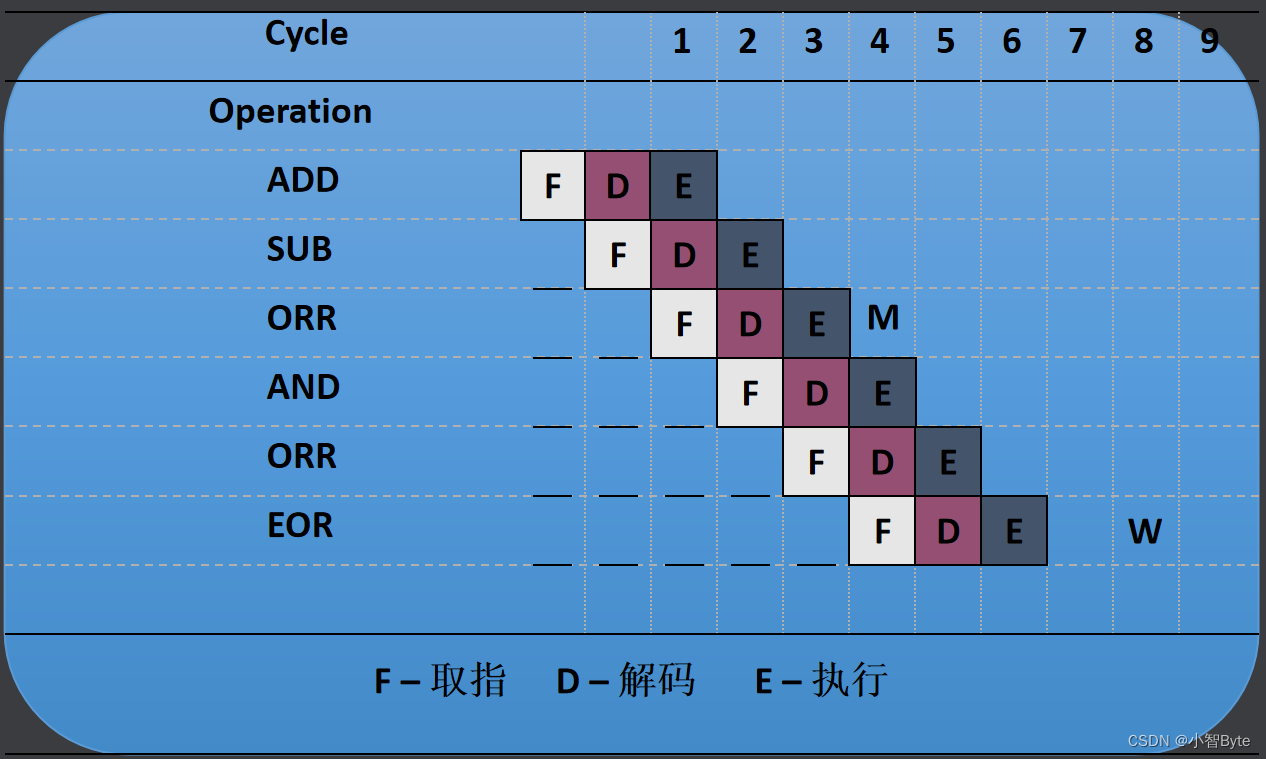
4、ARM异常处理
一、异常处理 1、异常 概念 处理器在正常执行程序的过程中可能会遇到一些不正常的的事件发生,这时处理器就要将当前的程序暂停下来转去处理这个异常的事件,异常事件完成后再返回到之前被异常打断的点继续执行 2、异常处理机制 不同的处理器对异常的…...

【Element-UI】CUD(增删改)及form 表单验证(附源码)
目录 一、导言 1、引言 2、作用 二、CUD 1、增加修改 1.1、添加弹窗 1.2、定义变量 1.3、定义方法 1.4、完整代码 2、删除 2.1、定义方法 三、表单验证 1、添加规则 2、定义规则 3、提交事件 4、前端完整代码 一、导言 1、引言 增删改是计算机编程和数据库管理…...

2024年高新技术企业认定标准
1高新技术企业认定八大条件是什么 (1)企业申请认定时须注册成立一年以上。 (2)企业通过自主研发、受让、受赠、并购等方式,获得对其主要产品(服务)在技术上发挥核心支持作用的知识产权的所有权。 (3)对企业主要产品(服务)发挥核心支持作用的技术属于《国家重点支持的…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
