Python经典练习题(四)
文章目录
- 🍀第一题
- 🍀第二题
- 🍀第三题
🍀第一题
题目:打印出如下图案(菱形):

我们首先分析一下,本题实现的步骤主要有两个,分别是前四行和后三行
- 前四行:第一行三空格+一*,第二行两空格+三*,第三行一空格+五*,第四行五空格+七*
- 后三行:第一行一空格五*,第二行两空格+三*,第三行三空格+一*
这里我们就可以找到规律了,如果以行为函数的参数,我们不妨将其设定为外循环的参数
代码如下
def f1(rowup): # 前四行for i in range(rowup):for j in range(rowup - i):print(' ',end='')for k in range(2 * i +1):print("*",end='')print()def f2(rowdown): # 后三行for i in range(rowdown):for j in range(i + 2):print(" ",end='')for k in range(5- 2 * i):print("*",end='')print()
运行结果

🍀第二题
有一分数序列:2/1,3/2,5/3,8/5, 13/8,21/13…求出这个数列的前20项之和。
def generate_fibonacci(n):fib = [0, 1] # 初始化斐波那契数列的前两项while len(fib) < n:next_fib = fib[-1] + fib[-2] # 计算下一项fib.append(next_fib) # 将下一项添加到列表中return fib# 生成斐波那契数列的前n项
n = 23 # 你可以替换成任何你想要的项数
fibonacci_sequence = generate_fibonacci(n)
sum_numbers= []for i in range(20):result = float(fibonacci_sequence[3:][i] / fibonacci_sequence[2:][i])sum_numbers.append(result)
print(sum(sum_numbers))
本题我的思路采用列表切片,看起来有点傻,但是能做出来就是好滴
运行结果如下

🍀第三题
题目:求1+2!+3!+…+20!的和。
本题采用三种方法进行求解
方法一:使用循环计算阶乘和求和
def factorial(n):result = 1for i in range(1, n + 1):result *= ireturn resultn = 20
total = sum(factorial(i) for i in range(1, n + 1))
print("方法一的结果:", total)
方法一:使用循环计算阶乘和求和
这个方法使用了一个for循环来计算每个数字的阶乘,然后将它们相加以得到最终的和。具体思路如下:
- 创建一个函数factorial(n),它接受一个整数n作为输入,并返回n的阶乘。
- 在主程序中,通过一个for循环遍历从1到20的所有数字,分别调用factorial()函数来计算它们的阶乘。
- 将每个阶乘值加到一个累加器变量中,最终得到总和。
方法二:使用递归计算阶乘和求和
def factorial(n):if n == 0:return 1else:return n * factorial(n - 1)n = 20
total = sum(factorial(i) for i in range(1, n + 1))
print("方法二的结果:", total)
方法二:使用递归计算阶乘和求和
这个方法使用了递归来计算每个数字的阶乘,然后将它们相加以得到最终的和。具体思路如下:
- 创建一个函数factorial(n),它接受一个整数n作为输入,并返回n的阶乘。
- 在factorial()函数内部,使用递归来计算阶乘。基本情况是当n为0时,阶乘为1;否则,递归调用factorial(n-1)并将结果与n相乘。
- 在主程序中,通过一个for循环遍历从1到20的所有数字,分别调用factorial()函数来计算它们的阶乘。
- 将每个阶乘值加到一个累加器变量中,最终得到总和。
方法三:使用预先计算好的阶乘值求和
def precompute_factorials(n):factorials = [1]for i in range(1, n + 1):factorials.append(factorials[-1] * i)return factorialsn = 20
factorials = precompute_factorials(n)
total = sum(factorials[i] for i in range(1, n + 1))
print("方法三的结果:", total)
方法三:使用预先计算好的阶乘值求和
这个方法首先预先计算了1到20的所有数字的阶乘值,然后直接使用这些值来求和。具体思路如下:
- 创建一个函数precompute_factorials(n),它接受一个整数n作为输入,并返回一个包含1到n的所有数字的阶乘值的列表。
- 在precompute_factorials()函数内部,使用一个for循环来计算1到n的所有数字的阶乘,并将它们存储在列表中。
- 在主程序中,调用precompute_factorials(20)来获取1到20的所有数字的阶乘值列表。
- 使用一个for循环遍历从1到20的所有数字,直接从阶乘值列表中取出对应的阶乘值,并将它们相加以得到总和。

挑战与创造都是很痛苦的,但是很充实。
相关文章:

Python经典练习题(四)
文章目录 🍀第一题🍀第二题🍀第三题 🍀第一题 题目:打印出如下图案(菱形): 我们首先分析一下,本题实现的步骤主要有两个,分别是前四行和后三行 前四行:第一…...

Mac Pro在重装系统时提示“未能与恢复服务器取得联系”
检查网络连接: 确保你的Mac Pro连接到稳定的网络。尝试更换其他网络,例如切换到不同的Wi-Fi或使用有线连接。 系统时间校正: 错误的系统时间有时会导致与恢复服务器的连接问题。在恢复模式下打开终端(在实用工具菜单中选择终端&a…...

【C/C++】指针常量、常量指针、指向常量的常指针
目录 1.概念2. const pointer3. pointer to a constant3.1 (pointer to a constant)-constant3.2 poiner-constant3.3 (pointer to a constant)-variable3.4 poiner-variable3.5 多层级关系时的兼容3.6 用处 4. a constant pointer to a constant 1.概念 首先明确这几个术语的…...
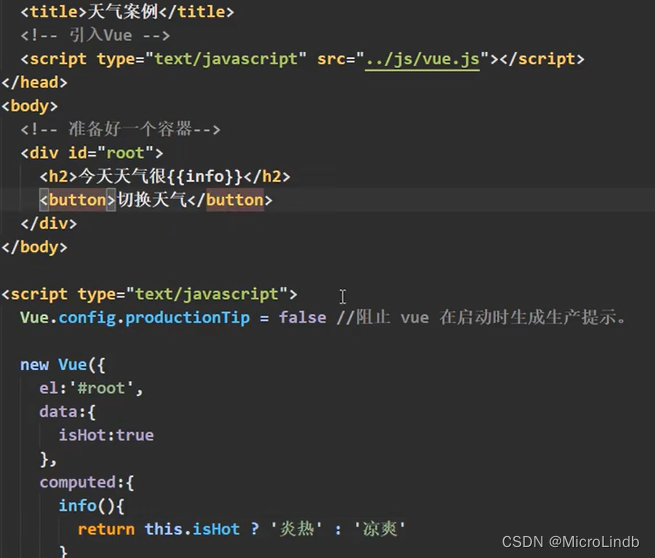
【VUE复习·4】计算属性computed:原理、完整写法(不常用)、与 methods 的区别、简写(最常用)、应用案例!
总览 1.简介计算属性 2.computed 与 methods 的区别 3.computed 的简写(不修改计算属性,只显示) 4.经典应用场景 一、计算属性 1.为什么需要计算属性? 首先,如果我们要写一个插值语法,而 {{ }} 内的内容…...

Linux 基本语句_编译C过程
Linux撰写C语言并编译的过程 1、预处理 将所有的#define删除,并且展开所有的宏定义,并且处理所有的条件预编译指令,比如#if #ifdef #elif #else #endif等。处理#include预编译指令,将被包含的文件插入到该预编译指令的位置。删除…...

MYSQL8解压版 windows 主从部署步骤及配置(包含配置文件,教程文件,免积分下载)
MYSQL8解压版 windows 主从部署步骤及配置 一.安装MSYQL 这里只讲大概,详细步骤、my.ini文件、安装包等会在页尾文件中(正常情况按首个mysql安装,只是名字有区别) 1.主库my.ini配置 [mysqld] #典型的值是5-6GB(8GB内存),8-11GB(16GB内存), 20-25GB(32GB内存)&…...

RabbitMQ的基本介绍
什么是MQ 本质是一个队列,只不过队列中存放的信息是message罢了,还是一种跨进程的通信机制,用于上下游传递信息。在互联网架构中,MQ是一种非常常见的上下游“逻辑解耦物理解耦”的消息通信服务。使用了MQ之后,信息发送…...
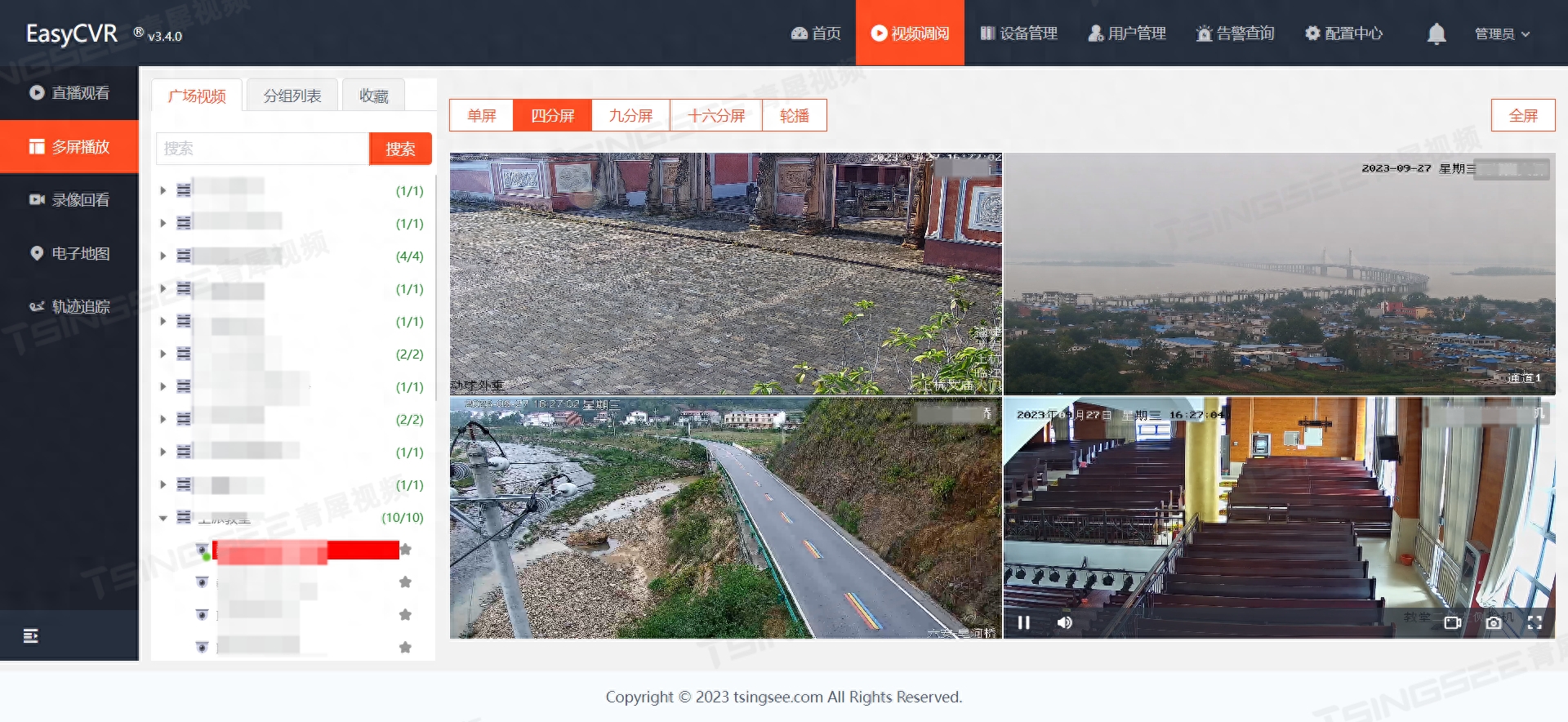
AI智能视频监控技术如何助力美好乡村建设?
随着城市化发展,很多乡村设施也在逐渐完善,智能监控也成了乡村发展必不可少的一环,智能视频监控应该在乡村建设里如何发挥作用呢? 1、有效提升安全意识 通过在乡村重要区域、公共场所、道路等设置智能视频监控设备,可…...

【网络安全】2023年堡垒机品牌大全
随着大家网络安全意识的增加,随着国家等保政策的严格执行,越来越多的企业开始采购堡垒机。这里就给大家总结了部分堡垒机品牌,让大家参考参考。 2023年堡垒机品牌大全 1、行云堡垒 2、JumpServer 3、安恒 4、骞云 5、齐治 6、阿里云 …...
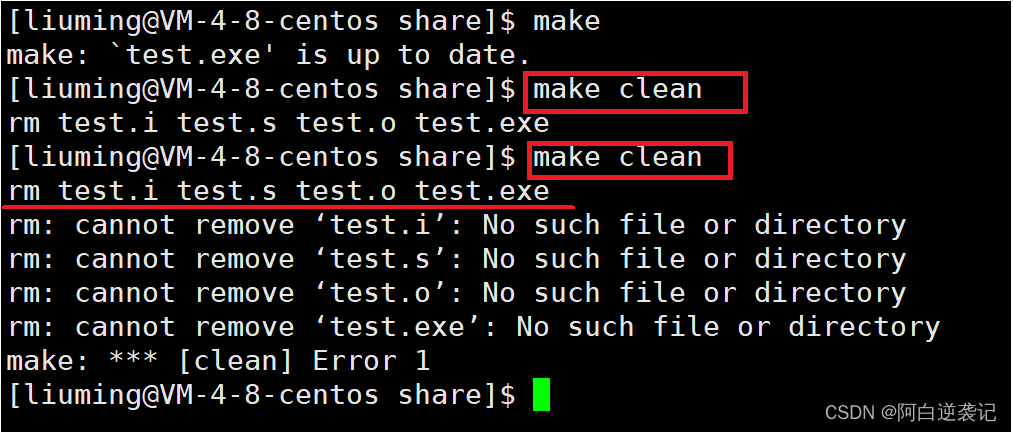
makefile相关知识的讲解
目录 makefile文件的介绍 step1:手动创建一个makefile文件 step2:在文件当中编辑指定的命令 step3:退出makefile文件并使用make执行文件当中的命令 step4:使用clean指令清除生成的文件 makefile当中的命令编写方式 目标文件和依…...
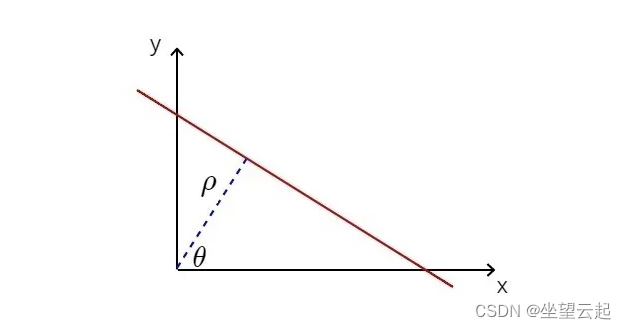
OpenCV中的HoughLines函数和HoughLinesP函数到底有什么区别?
一、简述 基于OpenCV进行直线检测可以使用HoughLines和HoughLinesP函数完成的。这两个函数之间的唯一区别在于,第一个函数使用标准霍夫变换,第二个函数使用概率霍夫变换(因此名称为 P)。概率版本之所以如此,是因为它仅分析点的子集并估计这些点都属于同一条线的概率。此实…...
Xilinx FPGA 程序固化重新上电程序不运行的问题
问题描述 FPGA直接下载bit文件,功能正常。 FPGA擦除FLASH,烧写FLASH,正常。 电源断电,重新上电,FALSH里面的程序没有启动,FPGA程序没有跑起来。–FLASH启动不正常。 解决办法 在XDC约束文件里边增加约束: ## Configuration options, can be used for all designs se…...
c++ 使用rapidjson对数据序列化和反序列化(vs2109)
RapidJSON是腾讯开源的一个高效的C JSON解析器及生成器,它是只有头文件的C库,综合性能是最好的。 1. 安装 在NuGet中为项目安装tencent.rapidjson 2. 引用头文件 #include <rapidjson/document.h> #include <rapidjson/memorystream.h> #…...

4.迭代最近点ICP及非线性优化求解
使用非线性优化方法求解ICP 文章目录 使用非线性优化方法求解ICP前情提要ICP问题回顾对矩阵变量求导数 ICP问题的非线性解法代码示例 欢迎访问个人网络日志🌹🌹知行空间🌹🌹 前情提要 在迭代最近点算法ICP及SVD求解中介绍了ICP问…...
【redis总结】
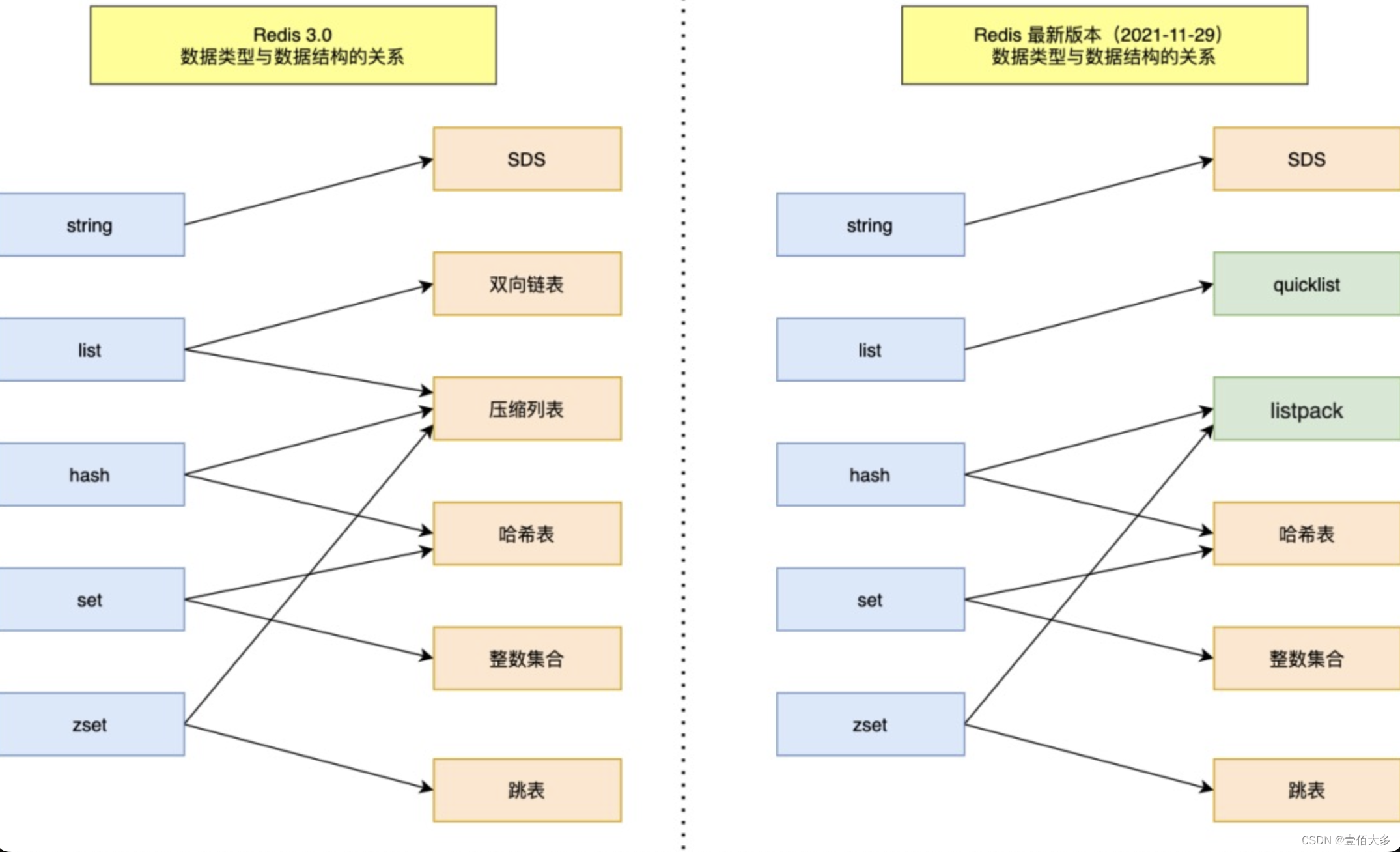
文章目录 1、redis简介2、为什么要选择redis做缓存3、数据结构4、redis多线程模型redis6.0的变化 5、redis持久化AOF的实现过程RDB的实现过程 6、redis集群的搭建7、 redis过期删除和淘汰策略8、redis的内存淘汰策略 1、redis简介 Redis(Remote Dictionary Server&…...

图数据库:释放关系的力量
【squids.cn】 全网zui低价RDS,免费的迁移工具DBMotion、数据库备份工具DBTwin、SQL开发工具等 在数据管理领域,图数据库已经成为一种强大的工具,它彻底改变了我们处理和分析复杂关系的方式。与依赖表和列的传统关系数据库不同,图…...

Windows系统如何临时关闭“Windows安全中心实时保护”
前言 启动windows depender实时保护可能会使系统不太流畅,也可能会导致我们的程序无法正常运行,因为它会拦截或搜索我们的正常工作。 暂时关闭windows depender的实时保护对许多用户来说非常重要。 一、Win10系统关闭方法 打开Windows安全中心&#…...
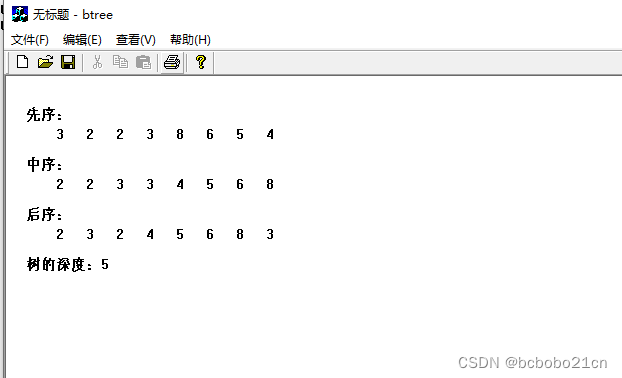
二叉树MFC实现
设有一颗二叉树如下; 这似乎是一颗经常用作示例的二叉树; 对树进行遍历的结果是, 先序为:3、2、2、3、8、6、5、4, 中序为:2、2、3、3、4、5、6、8, 后序为2、3、2、4、5、6、8、3;…...

Nginx之客户并发数限制解读
目录 基本介绍 配置指令 limit_conn_zone limit_conn 其他 limit_rate limit_rate_after limit_req_zone limit_req 基本介绍 在我们进行系统开发设计中,要考虑服务器流量异常,负载过大等问题。对于大流量恶意的攻击访问,会带来带宽…...
白捡一个存储型XSS
本文由掌控安全学院 - 杳若 投稿 起因 利用fofa搜索时发现 org"China Education and Research Network Center" && body"/register" 任意用户注册 在找到该CMS的时候发现存在任意用户注册的情况 http://xxxx.edu.cn/student/Register.ashx …...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
