力扣算法题:35、搜索插入位置.java版
版本说明
当前版本号[20230928]。
| 版本 | 修改说明 |
|---|---|
| 20230928 | 初版 |
35.搜索插入位置
点击此处跳转到力扣页面
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums为 无重复元素 的 升序 排列数组-104 <= target <= 104
思路
可以点击此篇博客看二分查找算法相关的图解:究竟是什么样的讲解二分查找算法的博客让我写了三小时???
这道题目是一个经典的二分查找问题,要求在一个排序数组中找到目标值的索引,如果目标值不存在,则返回它将被按顺序插入的位置。
解题思路如下:
-
首先,定义两个指针 i 和 j,分别指向数组的首部和尾部。
-
通过 while 循环,不断缩小搜索的范围,直到 i 大于 j。
-
在循环中,计算中间位置 m = (i + j) >>> 1(无符号右移一位,等价于除以2)。
-
如果目标值小于等于中间值 nums[m],则说明目标值可能在左半部分,将 j 更新为 m - 1。
-
如果目标值大于中间值 nums[m],则说明目标值可能在右半部分,将 i 更新为 m + 1。
-
重复上述步骤,直到找到目标值或者搜索范围缩小到 i 大于 j(找到目标值)。
-
返回 i 的值,即为目标值的索引或者插入位置。
该算法的时间复杂度为 O(log n),因为每次都将搜索范围缩小为原来的一半,直到找到目标值或搜索范围为空。
代码
基础版
基础版代码具体的工作流程如下:
- 首先,定义两个指针
i和j,分别指向数组的首部和尾部。 - 通过
while循环,在满足i <= j的条件下进行查找。 - 在循环中,计算中间位置
m,使用无符号右移一位(i + j) >>> 1来避免溢出。 - 如果目标值
target小于当前中间值a[m],则说明目标值可能在左半部分,将j更新为m - 1。 - 如果中间值
a[m]小于目标值target,则说明目标值可能在右半部分,将i更新为m + 1。 - 如果中间值
a[m]等于目标值target,则说明找到了目标值,直接返回索引m。 - 重复上述步骤,直到找到目标值或搜索范围缩小到
i > j。 - 最后,如果找到了目标值,则返回对应的索引;如果没有找到,则返回插入位置
i。
注:原始代码中返回的是 -1,但实际应该是返回插入位置 i。
public int searchInsert(int[] a, int target) {int i = 0, j = a.length - 1;while (i <= j) {int m = (i + j) >>> 1;if (target < a[m]) {j = m - 1;} else if (a[m] < target) {i = m + 1;} else {return m;}}return i; // 原始 return -1
}
优化版
普通版与优化版这两段代码实际上是相同的,只是变量名不同。
优化之处在于代码的可读性和简洁性,通过使用有意义的变量名和清晰的逻辑结构,使得代码更易于理解。返回值即为插入位置,并能处理元素重复的情况。
将 target < a[m] 与 target = a[m] 的情况优化在一起target <= nums[m] ,并少了一层的判断,这样的优化并不会改变算法的时间复杂度和核心思想,但可以提高代码的可读性和可维护性。
都是使用二分查找在给定的排序数组中找到目标值的索引,如果目标值不存在,则返回它将被按顺序插入的位置。
class Solution {public int searchInsert(int[] nums, int target) {int i = 0;int j = nums.length - 1;while (i <= j){int m = (i + j) >>> 1;if(target <= nums[m]){j = m -1 ;}else{i = m + 1 ;}}return i;}
}
总结
这道题目是要求在给定的排序数组中,使用二分查找的算法找到目标值的索引,如果目标值不存在,则返回它将被插入的位置。
总结一下解题思路和步骤:
-
定义两个指针
i和j,分别指向数组的首部和尾部。 -
使用
while循环,在满足i <= j的条件下进行查找。 -
在循环中,通过计算中间位置
m来获取中间元素的索引,使用无符号右移一位(i + j) >>> 1来避免溢出。 -
如果目标值
target小于当前中间值a[m],则更新j = m - 1,因为目标值可能在左半部分。 -
如果中间值
a[m]小于目标值target,则更新i = m + 1,因为目标值可能在右半部分。 -
如果中间值
a[m]等于目标值target,则说明找到了目标值,直接返回索引m。 -
重复上述步骤,直到找到目标值或者搜索范围缩小到
i > j。 -
最后,如果找到了目标值,则返回其索引;如果没有找到,则返回插入位置
i。
这种二分查找算法的时间复杂度为 O(log n),其中 n 是数组的长度。通过在每一次比较中将搜索范围缩小一半,可以高效地找到目标值或插入位置。
在编码实现时,需要注意边界条件、循环终止条件和变量更新的逻辑。通过理解并正确实现这个二分查找算法,可以在排序数组中快速地找到目标值的索引或插入位置。
相关文章:

力扣算法题:35、搜索插入位置.java版
版本说明 当前版本号[20230928]。 版本修改说明20230928初版 35.搜索插入位置 点击此处跳转到力扣页面 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必…...
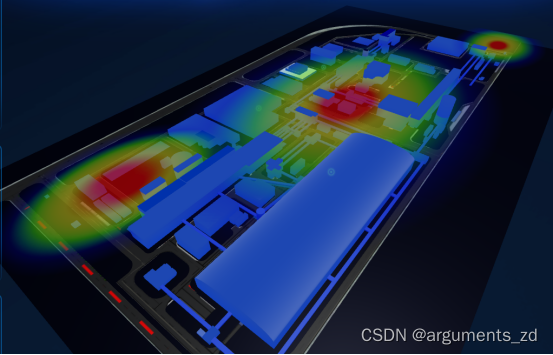
七、热力图展示
在开发3d模型之中,热力图是非常常见的需求,比如需要了解人口密度,空气质量,热力分布等这些都需要热力图来展示,那么3d常见的热力图是怎么实现的呢,现在我们就来看看。先看效果图。 思路: 1引入h…...

基于微信小程序的新闻发布平台小程序设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...

【论文阅读】Directional Connectivity-based Segmentation of Medical Images
目录 摘要介绍方法效果结论 论文:Directional Connectivity-based Segmentation of Medical Images 代码:https://github.com/zyun-y/dconnnet 摘要 出发点:生物标志分割中的解剖学一致性对许多医学图像分析任务至关重要。 之前工作的问题&…...

借“牛油果”爆款出圈,甜啦啦的底牌只是“价格”?
上架10日,累计销量超过500万杯。近日,甜啦啦新品“超牛牛油果”瞬间成为门店新晋“爆款”。势头正劲的甜啦啦乘胜追击,袒露了自己的新目标,计划2025年进军北美、欧洲等地区,并在同年开启上市征途。 甜啦啦袒露的新目标…...
【C语言】快速排序
文章目录 一、hoare版本二、挖坑法三、前后指针法四、非递归快排五、快速排序优化1、三数取中选key值2、小区间优化 六、代码测试 一、hoare版本 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素…...
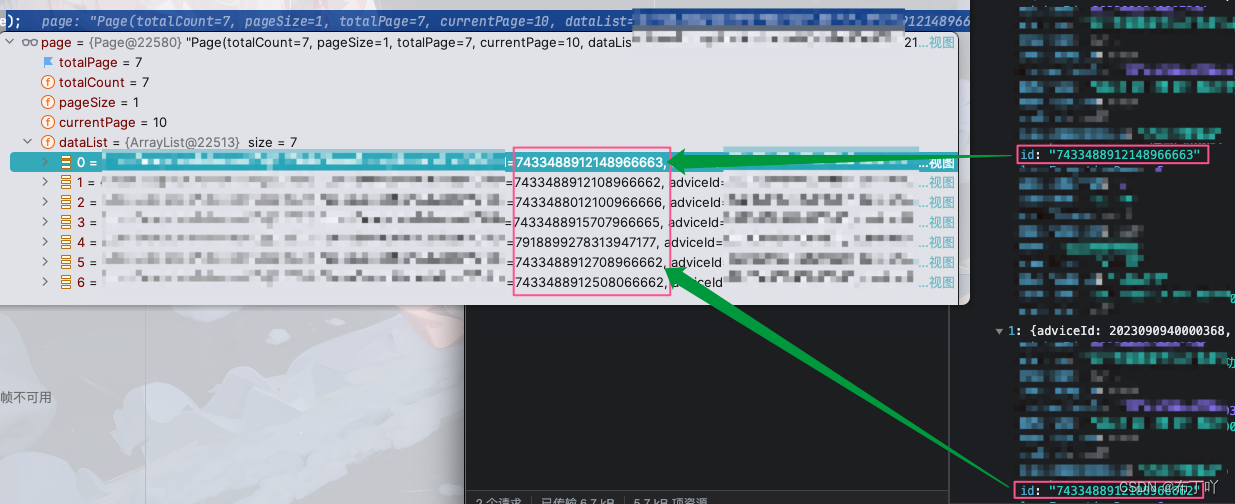
Java列表查询Long(id)到前端转换出错
Java列表查询Long到前端转换出错 问题描述排查思路思路一:SQL问题思路二:Long类型转换出错 解决方法 问题描述 做了一个列表查询功能,本来不应该有啥大问题的,但是往往事与愿违。 诶,你越觉得不可能出问题,…...

react import爆红
如上所示,会标红, 解决办法:在vscode内部SHiftCtrlP 输入Reload window, 如上的第一个,选中后回车,标红就没了,非常好用。...
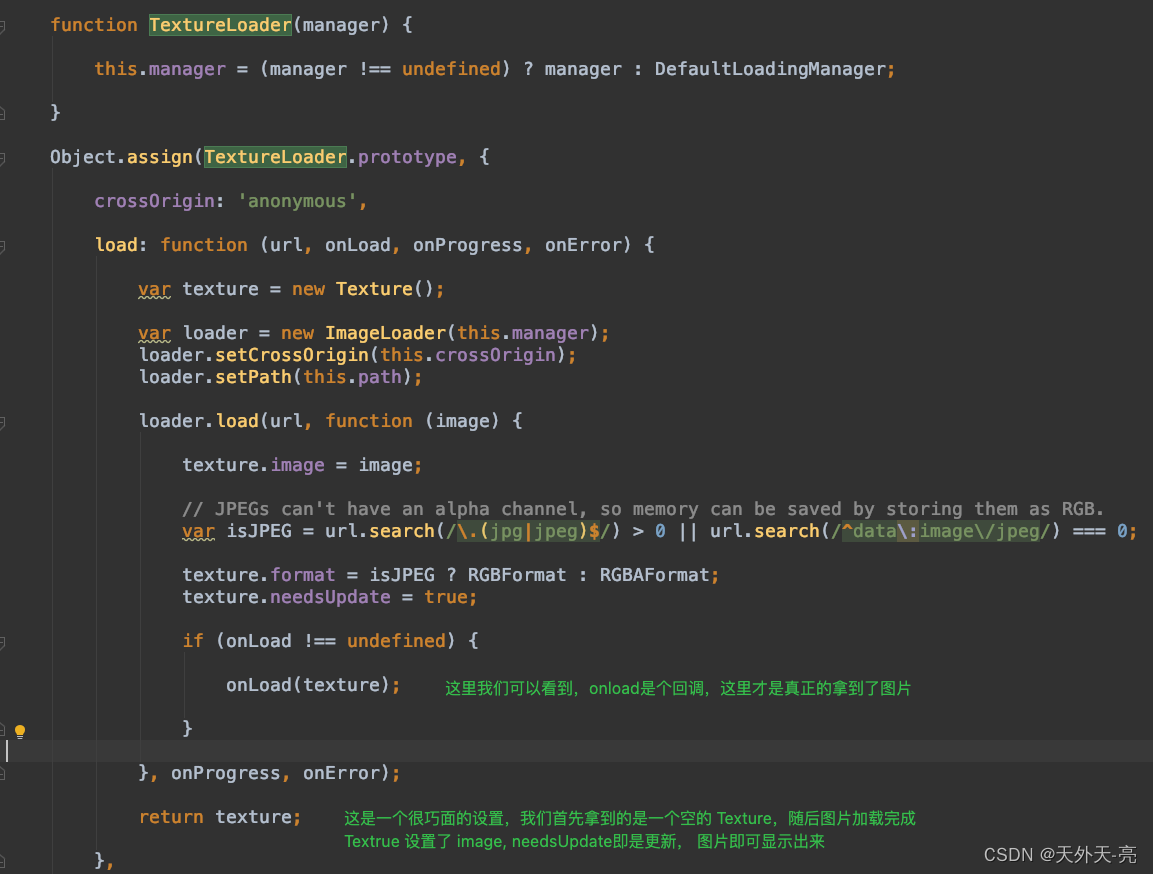
ThreeJS-3D教学三:平移缩放+物体沿轨迹运动
我们在项目中会有一些这样的需求,我们可视化一个场景,需要俯视、平移、缩放,方便观察场景中的数据或者模型,之所以把这个案例拿出来 1、这是个很实用的需求,我相信很多人会用到 2、我自己认为在实际案例中我们可以学习…...
玩玩“小藤”开发者套件 Atlas 200I DK A2 之VSCode远程连接
玩玩“小藤”开发者套件 Atlas 200I DK A2 之VSCode远程连接 0. 背景1. VSCode 安装 Remote - SSH 插件2. 安装 OpenSSH 组件3. VSCode SSH 连接 Atlas 200I DK A24. 打开远程文件夹 0. 背景 总所周知,英伟达的GPU供不应求,还各种限制。华为推出了升腾A…...

安装python中tensorflow和keras==2.2.0的路程
1.python中安装Keras2.3.0 你可以使用pip来安装特定版本的Keras。在命令行中运行以下命令: pip install keras2.3.0这将会下载并安装Keras的2.3.0版本及其相应的依赖项。请确保你的Python环境已经配置好,并且有足够的权限来安装软件包。2.python 中安装…...

Linux命令历史记录管理:使用history命令提高工作效率
文章目录 引言1.1 关于history命令1.2 history命令的作用和用途 基本用法2.1 查看历史命令列表2.2 执行历史命令2.3 使用历史命令编号 历史命令记录和保存3.1 历史命令的存储位置3.2 修改历史命令记录数量3.3 清除历史命令记录 搜索历史命令4.1 使用关键字搜索4.2 按日期和时间…...

Armv9 Cortex-A720的L1 memory system 和 L1 Cache
思考: L1 System memory和L1 Cache是什么关系?L1指令cache禁用时,指令cache就真的不会缓存了吗?此时还会出现缓存不一致的情况吗?L1 data cache禁用时,L1 data cache就真的不会缓存了吗?此时还会出现缓存不一致的情况吗?在下电的时候,cache有什么自动的行为?有没有in…...

使用超声波清洗机洗眼镜有哪些注意事项、高颜值超声波清洗机推荐
眼镜,对于许多人来说,不仅仅是矫正视力的工具,更是日常生活的重要伴侣。但是,眼镜的清洁问题却常常让人感到困扰。镜片上的污渍、指纹、甚至小划痕,都让眼镜的使用体验大打折扣。幸运的是,随着科技的进步&a…...
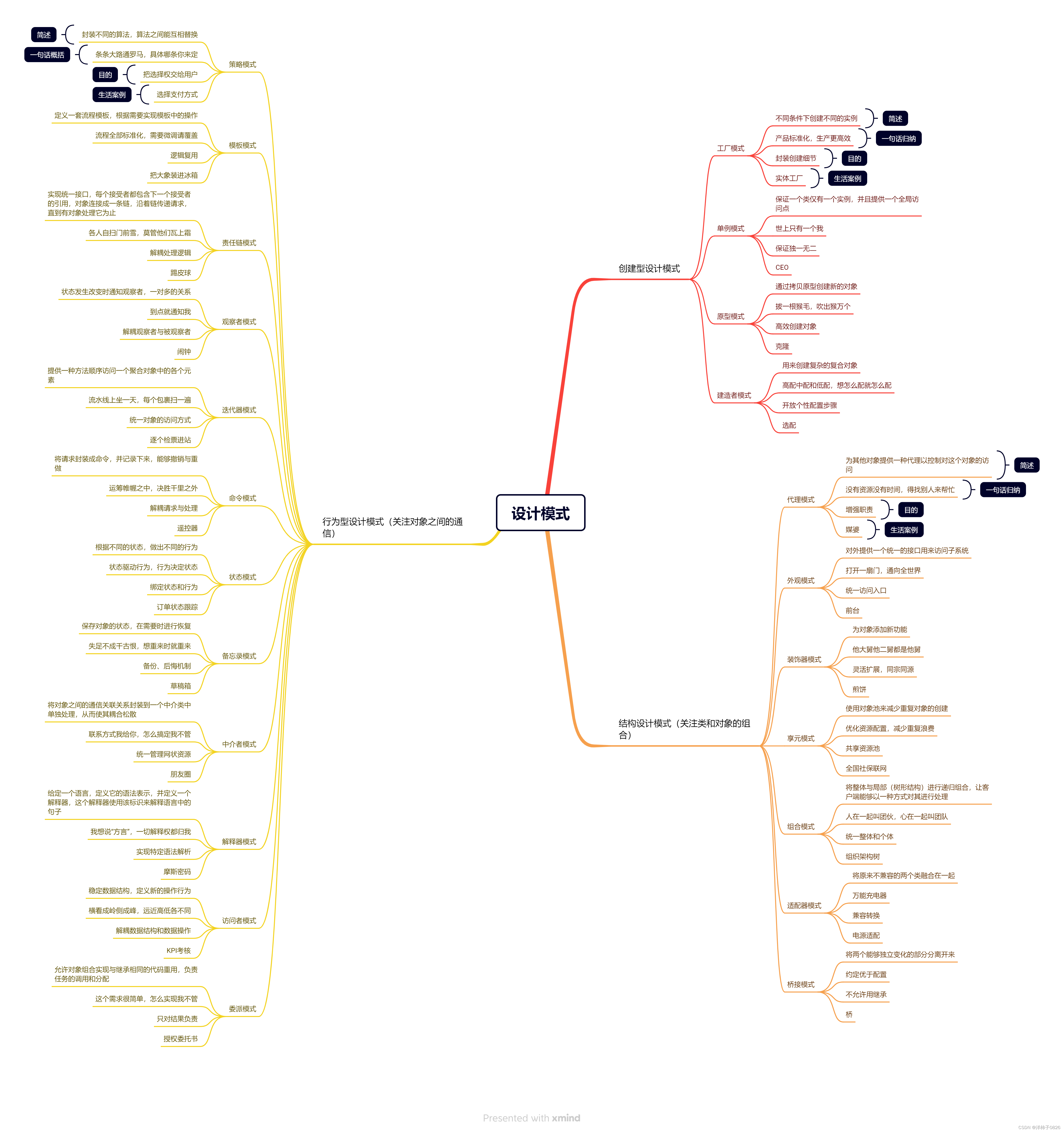
23种设计模式汇总详解
设计原则 中文名称英文名称含义解释单一职责原则Single Responsibility Principle(SRP)任何一个软件模块都应该只对某一类行为者负责一个类只干一件事,实现类要单一开闭原则Open-Close Principle(OCP)软件实体(类、模块、函数等)应该是可以扩…...

stream流的filter和map过滤
详情页面 // 过滤出身高大于 170 的记录 personList.stream().filter((item)->item.getHeight() > 170).forEach(System.out::println);//从对象中提取age。并过滤年龄 List<Integer> nameListstudentList.stream().map(StudentInfo::getAge).filter(f->f>…...
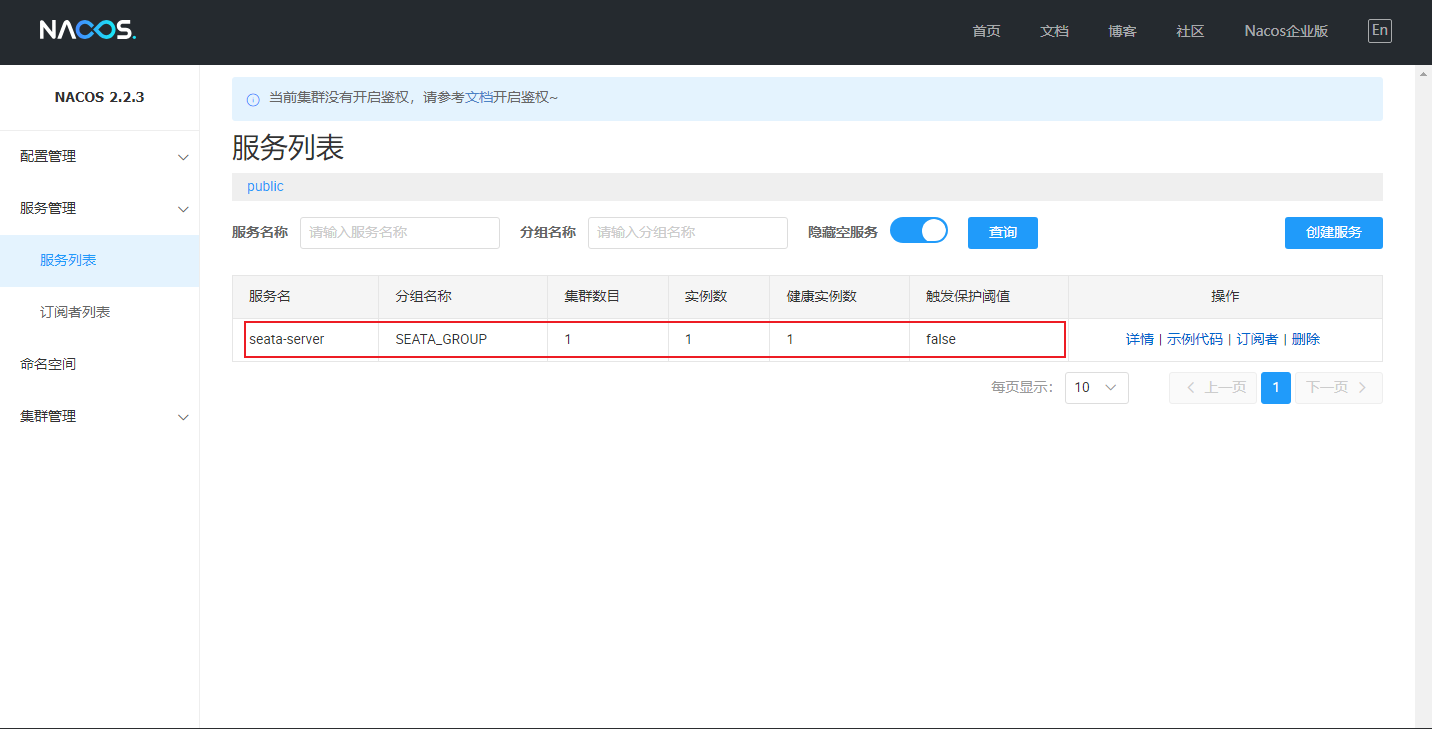
Linux 环境下使用 Docker 部署 Seata 1.7.1 (图文教程)
目录 前言环境准备创建数据库安装 Seata下载镜像自定义配置文件自定义配置启动 Seata 开源项目微服务商城项目 前后端分离项目联系我 前言 本篇参考 Seata 官方部署文档 在 Linux 环境通过 Docker 部署 Seata 1.7.1 版本,以及为 youlai-mall 开源商城版本的升级做…...

Aruba CX交换机 VSF配置
目前 Aruba CX 交换机中的 6300F 和 6300M 支持 VSF 功能,要求同型号堆叠。 6300 交换机仅仅最后 4 个 SFP56 端口支持 VSF link 6200F : all uplink ports with 10G speed can be configured as VSF link 6200F: VSF allows stacks to be formed using any combin…...

使用ElementUI结合Vue完善主页的导航菜单和书籍管理以及后台数据分页查询
目录 动态树 数据表 案列 书籍管理 动态树 动态树(Dynamic tree)是一种数据结构,它可以在树中动态地插入、删除和修改节点。与静态树不同,静态树的节点是固定的,一旦构建完成就无法再进行修改。而动态树可以在运行时…...

子序列问题集合
子序列问题 删除一次得到的最大和最大子数组和最长公共子序列:最长上升子序列(要输出序列,和最大长度)1.dp2.贪心二分 导弹拦截 (最长上升/下降子序列长度) 删除一次得到的最大和 class Solution { public:…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
