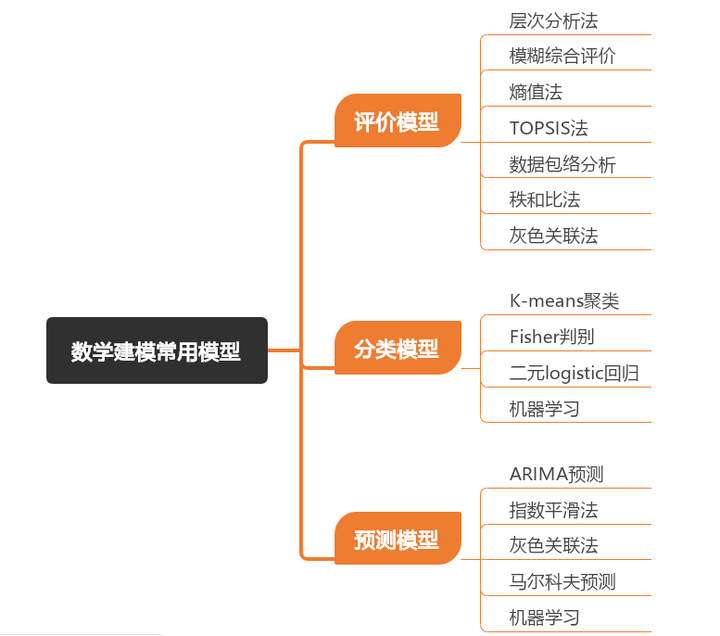
数学建模常用模型
作为数学建模的编程手还掌握一些各类模型常用算法,数学建模评价类模型、分类模型、预测类模型比较常用的方法总结如下:
接下来对这些比较典型的模型进行详细进行介绍说明。
一、评价模型
在数学建模中,评价模型是比较基础的模型之一,通常根据问题的特点和需求,设计合适的评价标准和指标,对不同方案或模型的性能进行评估和比较,以帮助做出决策。典型模型包括:层次分析法、模糊综合评价、熵值法、TOPSIS法、数据包络分析、秩和比法、灰色关联法。
1、层次分析法
(1)基本思想
AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。它通过构建层次结构,将复杂的决策问题分解成多个层次,并使用专家判断和比较来确定各个因素的权重,从而得出最终决策结果。比较有效地应用于那些难以用定量方法解决的课题。
(2)分析步骤
- 第一步:构造判断矩阵;
- 第二步:计算权重;
- 第三步:一致性检验。
(3)软件操作使用SPSSAU进行层次分析法,输入判断矩阵即可:
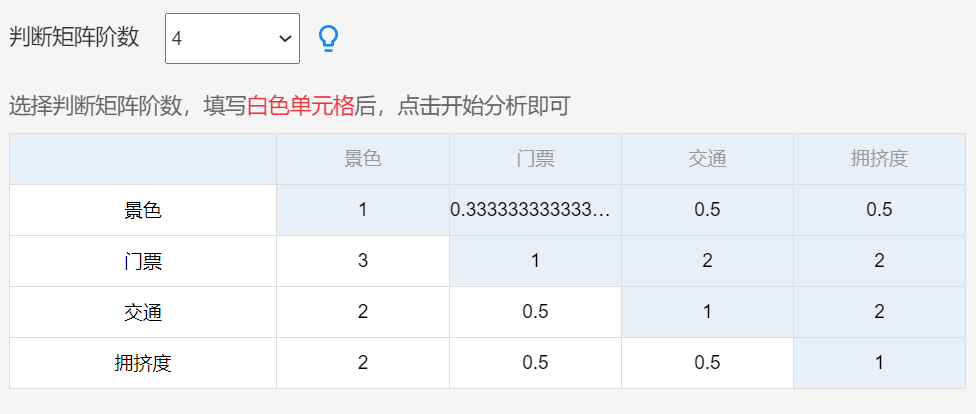
判断矩阵解读:门票相对于景色来讲,重要性更高,所以为3分;相反,景色相对于门票来讲,则为0.33333分。交通相对于景色来更重要为2分,其余类似下去。
AHP层次分析详细说明及案例操作解读请点击查看下方帮助手册:
AHP层次分析法帮助手册
2、模糊综合评价
(1)基本思想
模糊综合评价是一种处理具有模糊信息的评价方法。在模糊综合评价中,将模糊的评价指标通过隶属度函数转化为隶属度,然后根据权重给予不同指标不同的重要性。最后,通过对隶属度进行加权求和,得到一个综合评价结果。模糊综合评价方法能够有效处理不确定性和模糊性的问题,适用于现实世界中的复杂决策。
(2)分析步骤
- 第一步:确定评价指标和评语集;
- 第二步:确定权重向量矩阵A和构造权重判断矩阵R;
- 第三步:计算权重并进行决策评价。
(3)软件操作上传数据至SPSSAU系统,分析页面右侧选择【模糊综合评价】,将变量拖拽到右侧相应的分析框中,点击“开始分析”,操作如下图:
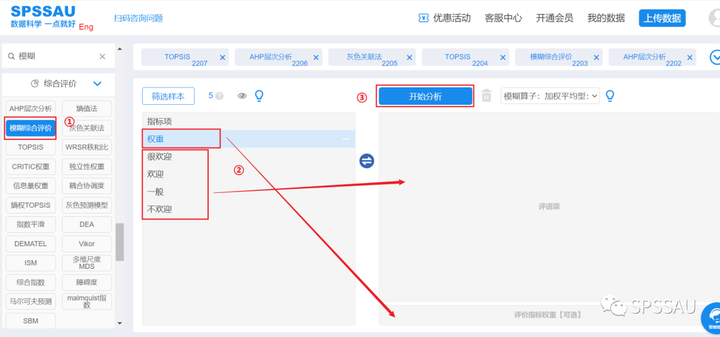
模糊综合评价详细说明及案例操作解读请点击查看下方帮助手册
模糊综合评价帮助手册
3、熵值法
(1)基本思想
熵值法是一种客观赋权法,用于确定各个指标在综合评价中的权重。熵值是不确定性的一种度量。信息量越大,不确定性就越小,熵也就越小;信息量越小,不确定性越大,熵也越大。因而利用熵值携带的信息进行权重计算,结合各项指标的变异程度,利用信息熵这个工具,计算出各项指标的权重,为多指标综合评价提供依据。
(2)分析步骤
- 第一步:数据标准化;
- 第二步:非负平移;
- 第三步:计算权重并进行决策评价。
(3)软件操作
上传数据至SPSSAU系统,分析页面右侧选择【熵值法】,将变量拖拽到右侧相应的分析框中,点击“开始分析”,操作如下图:
熵值法详细说明及案例操作解读请点击查看下方帮助手册
熵值法帮助手册
4、TOPSIS法
(1)基本思想
TOPSIS法是一种基于距离和相似性度量的多属性决策方法。TOPSIS法首先将多个备选方案与理想解进行比较,计算每个备选方案与理想解之间的相似性和距离。然后根据计算结果,评估和排序各个备选方案,选择最佳的方案。TOPSIS法能够较好地处理多属性决策问题,特别适用于需要考虑多个评价指标的情况。
(2)分析步骤
- 第一步:准备好数据,并且进行同趋势化处理(需要研究者自行处理);
- 第二步:数据归一化处理解决量纲问题(数据处理->生成变量,通常选择‘平方和归一化’);
- 第三步:找出最优和最劣矩阵向量(SPSSAU自动处理);
- 第四步:分别计算评价对象与正理想解距离D+或负理想解距离D-;
- 第五步:结合距离值计算得出接近程序C值,并且进行排序,得出结论。
(3)SPSSAU软件操作
上传数据至SPSSAU系统,分析页面右侧选择【TOPSIS法】;将变量拖拽到右侧分析框中;点击“开始分析”,操作如下图:

TOPSIS法详细说明及案例操作解读请点击查看下方帮助手册
TOPSIS法帮助手册
5、数据包络分析
(1)基本思想
数据包络分析DEA是一种多指标投入和产出评价的研究方法。其应用数学规划模型计算比较决策单元(DMU)之间的相对效率,对评价对象做出评价。
(2)分析步骤
- 第一步:确定决策单元与评价指标;
- 第二步:DEA模型选择;
- 第三步:计算效率评价;
- 第四步:效率分析和改进。
(3)SPSSAU软件操作
将数据上传至SPSSAU系统,分析页面右侧选择【DEA】,将变量拖拽到右侧相应分析框中,选择“DEA类型”,点击“开始分析”,操作如下图:
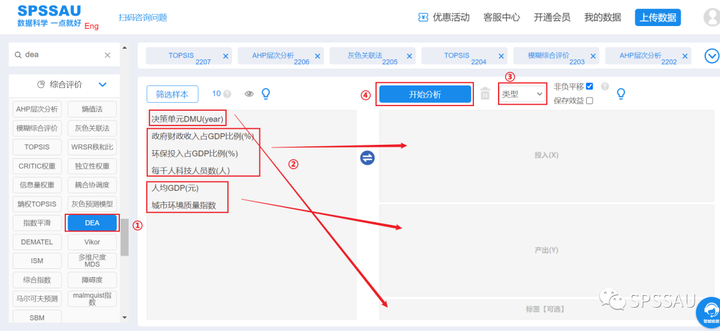
数据包络分析DEA详细说明及案例操作解读请点击查看下方帮助手册
数据包络分析DEA帮助手册
6、秩和比法
(1)基本思想
秩和比(RSR)方法是一种基于排序的模型比较方法。其实质原理是利用了RSR值信息进行各项数学计算,RSR值介于0~1之间且连续,通常情况下,该值越大说明评价越‘优’。
(2)分析步骤
- 第一步:列出原始数据,一行代表一个评价对象,一列代表一个评价指标。最终为m*n矩阵;
- 第二步:对m*n矩阵即原始数据进行计算秩值;
- 第三步:利用Step2的秩值,计算得到RSR值和RSR值排名;
- 第四步:列出RSR的分布表格情况并且得到Probit值;
- 第五步:计算回归方程;
- 第六步:进行排序,并且进行分档等级。
(3)软件操作
上传数据至SPSSAU系统,分析页面右侧选择【秩和比】,将变量拖拽到右侧相应分析框中,选择“编制方法”、“档次数量”,点击“开始分析”,操作如下图:
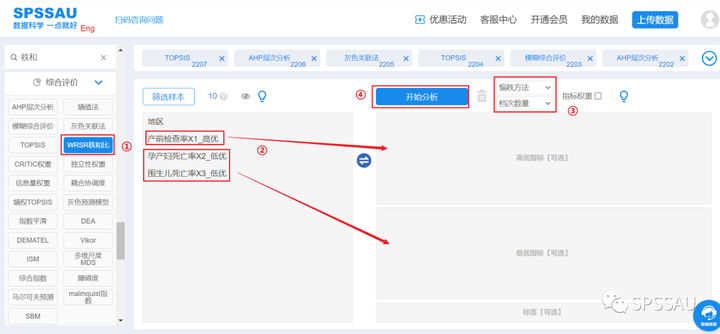
秩和比详细说明及案例操作解读请点击查看下方帮助手册
秩和比帮助手册
7、灰色关联法
(1)基本思想
灰色关联分析法通过研究数据关联性大小(母序列与特征序列之间的关联程度),通过关联度(即关联性大小)进行度量数据之间的关联程度,从而辅助决策的一种研究方法。
(2)分析步骤
- 第一步:确定母序列和特征序列,且准备好数据格式;
- 第二步:针对数据进行无量纲化处理(通常情况下需要);
- 第三步:求解母序列和特征序列之间的灰色关联系数值;
- 第四步:求解关联度值;
- 第五步:对关联度值进行排序,得出结论。
(3)软件操作
将数据上传至SPSSAU系统,分析页面右侧选择【灰色关联法】;将变量拖拽到右侧相应分析框中,选择“量纲化方式”,点击“开始分析”,操作如下图:
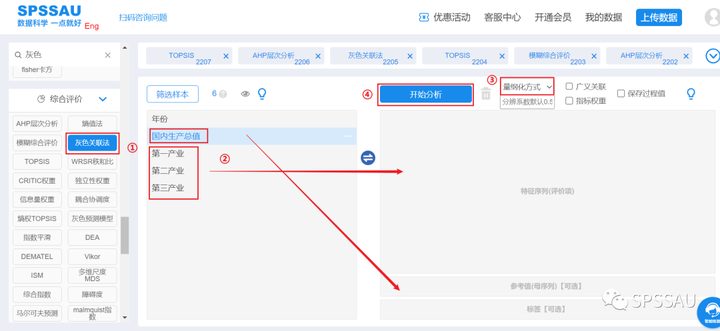
灰色关联法详细说明及案例操作解读请点击查看下方帮助手册
灰色关联法帮助手册
二、分类模型
数学建模的分类模型是指根据已知的分类标号将输入的数据集建立分类的数据挖掘方法。分类的目标是将数据的每个个案都尽可能准确地预测到一个目标分类中。典型模型包括K-means聚类、Fisher判别分析、二元logistic回归、决策树、随机森林、神经网络分类、K近邻算法等。
1、K-means聚类
(1)基本思想
K-means算法是典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。因为需要计算距离,所以决定了K-means算法只能处理数值型数据,而不能处理分类属性型数据。
(2)分析步骤
- 第一步:K-means算法首先需要选择K个初始化聚类中心
- 第二步:计算每个数据对象到K个初始化聚类中心的距离,将数据对象分到距离聚类中心最近的那个数据集中,当所有数据对象都划分以后,就形成了K个数据集(即K个簇)
- 第三步:接下来重新计算每个簇的数据对象的均值,将均值作为新的聚类中心
- 第四步:最后计算每个数据对象到新的K个初始化聚类中心的距离,重新划分
- 第五步:每次划分以后,都需要重新计算初始化聚类中心,一直重复这个过程,直到所有的数据对象无法更新到其他的数据集中。
(3)软件操作
将数据上传至SPSSAU系统,分析页面右侧选择【聚类】;将变量拖拽到右侧相应分析框中,点击“开始分析”,操作如下图:
添加图片注释,不超过 140 字(可选)
补充:SPSSAU在进行聚类分析时,将相应的数据类型放入右边的分析栏中,可自动识别数据进行定量or定类or混合数据的聚类分析。
- 当仅进行定量数据分析时,SPSSAU默认使用K-means聚类方法进行聚类;
- 当仅进行定类数据分析时,SPSSAU默认使用K-modes聚类方法进行聚类;
- 当进行混合型(定量+定类)数据分析时,SPSSAU将使用K-prototype聚类方法进行聚类。
聚类分析详细说明及案例操作解读请点击查看下方帮助手册
聚类分析帮助手册
2、Fisher判别分析
(1)基本思想
Fisher判别分析基本思想是通过将样本投影到一条直线上,使得同类样本间的距离尽可能小,不同类样本间的距离尽可能大,从而实现对样本的分类。
(2)软件操作
将数据上传至SPSSAU系统,分析页面右侧选择【判别分析】;将变量拖拽到右侧相应分析框中
判别分析详细说明及案例操作解读请点击查看下方帮助手册判别分析帮助手册
3、二元logistic回归
(1)基本思想
二元logistic回归分析是一种常用的分类方法,其基本思想是通过建立一个逻辑回归模型来对样本进行分类。将预测变量的线性组合转化为一个在0到1之间的概率值,然后以此概率值作为分类的依据。相对于其他分类方法,二元logistic回归分析具有模型简单、参数可解释性强等优点,在实际应用中得到了广泛的使用。
(2)分析步骤
第一步:建立二元logistic回归模型;第二步:对模型进行评估;第三步:应用模型进行分类预测。
(3)软件操作
将数据上传至SPSSAU系统,分析页面右侧选择【二元logit回归】;将变量拖拽到右侧相应分析框中,点击“开始分析”,操作如下图:
添加图片注释,不超过 140 字(可选)
二元logistic回归分析详细说明及案例操作解读请点击查看下方帮助手册
二元logistic回归分析帮助手册
4、机器学习
决策树、随机森林、神经网络、K近邻算法、朴素贝叶斯、支持向量机可归类为机器学习进行分类的这一类,有关六类典型机器学习算法可以下面这篇以往文章:
六种机器学习算法大揭秘:从决策树到神经网络,小白也能轻松掌握!
三、预测模型
1、ARIMA预测
(1)基本思想
ARIMA模型是最常见的时间序列预测分析方法,适用于平稳时间序列数据。它包括三个部分:自回归(AR)、差分(I)和移动平均(MA)。SPSSAU可以智能地找出最佳的AR模型,I即差分值和MA模型,并且最终给出最佳模型预测结果。当然,研究人员也可以自行设置自回归阶数p,差分阶数d值和移动平均阶数q,然后进行模型构建。
(2)软件操作
ARIMA预测详细说明及案例操作解读请点击查看下方帮助手册
ARIMA预测帮助手册
2、指数平滑法
(1)基本思想
指数平滑法常用于数据序列较少时使用,且一般只适用于中短期预测。对于长期趋势或复杂非线性关系的数据可能表现不佳。指数平滑可以继续拆分为一次平滑、二次平滑、三次平滑;一次平滑法为历史数据的加权预测,二次平滑法适用于具有一定线性趋势的数据,三次平滑法适用于具有一定曲线关系时使用。如果不设置平滑方法,SPSSAU将自动运行三种平滑方法,选择最优效果时对应的平滑方法。
指数平滑法中,初始值S0和平滑系数alpha是两个参数,用于确定预测模型的初始状态和对过去观察值的权重。
(2)软件操作
指数平滑法详细说明及案例操作解读请点击查看下方帮助手册:
指数平滑法帮助手册
3、灰色预测模型
(1)基本思想
灰色预测模型可针对数量非常少(比如仅4个),数据完整性和可靠性较低的数据序列进行有效预测。其利用微分方程来充分挖掘数据的本质,建模所需信息少,精度较高,运算简便,易于检验,也不用考虑分布规律或变化趋势等。但灰色预测模型一般只适用于短期数据、有一定指数增长趋势的数据进行预测,不建议进行长期预测。
(2)软件操作
灰色预测模型详细说明及案例操作解读请点击查看下方帮助手册
灰色预测模型帮助手册
4、马尔科夫预测
(1)基本思想
马尔可夫预测是一种基于马尔可夫链的预测方法。马尔可夫链是一个随机过程,具有马尔可夫性质,即未来状态的概率只取决于当前状态,与过去状态无关。马尔可夫预测利用这种性质来进行未来事件的预测。
马尔可夫预测涉及3个术语名词。
(2)软件操作
马尔可夫预测详细说明及案例操作解读请点击查看下方帮助手册
马尔科夫预测帮助手册
5、机器学习预测
机器学习是一种强大的技术,用于从数据中学习模式和规律,并利用这些知识进行预测。
有关六类机器学习算法说明,上周已经写过详细介绍,在此不再进行赘述。可点击下方文章进行学习:六种机器学习算法大揭秘:从决策树到神经网络,小白也能轻松掌握!
相关文章:

数学建模常用模型
作为数学建模的编程手还掌握一些各类模型常用算法,数学建模评价类模型、分类模型、预测类模型比较常用的方法总结如下: 接下来对这些比较典型的模型进行详细进行介绍说明。 一、评价模型 在数学建模中,评价模型是比较基础的模型之一&#x…...
Linux 基本语句_5_创建静态库|动态库
静态库 创建主函数:main.c 应用函数:add.c、sub.c、mul.c 创建calc.h文件作为头文件 生成可执行文件*.o文件 gcc -c add.c -o add.o ....包装*.o文件为静态库 ar -rc libmymath.a add.o sub.o mul.o编译静态库并指明创建静态库的位置 sudo gcc mai…...
【每日一题】2703. 返回传递的参数的长度
2703. 返回传递的参数的长度 - 力扣(LeetCode) 请你编写一个函数 argumentsLength,返回传递给该函数的参数数量。 示例 1: 输入:args [5] 输出:1 解释: argumentsLength(5); // 1只传递了一个值…...
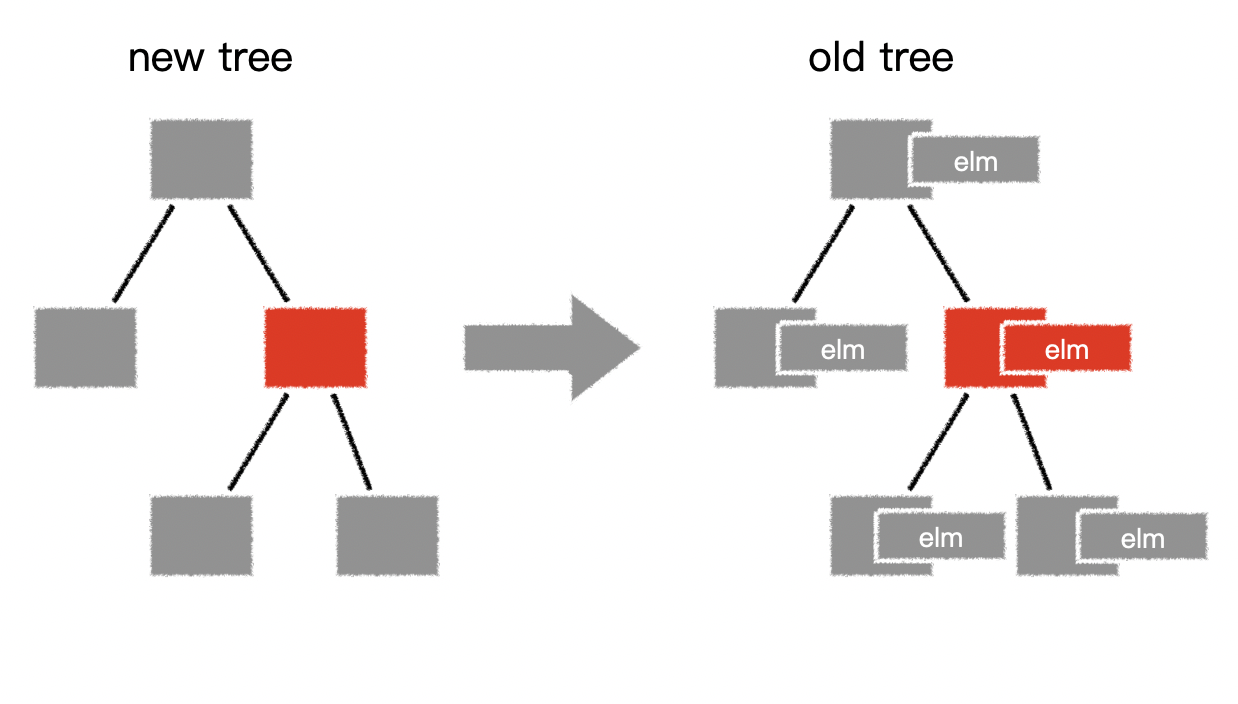
虚拟DOM详解
面试题:请你阐述一下对vue虚拟dom的理解 什么是虚拟dom? 虚拟dom本质上就是一个普通的JS对象,用于描述视图的界面结构 在vue中,每个组件都有一个render函数,每个render函数都会返回一个虚拟dom树,这也就意味…...

Linux配置命令
一:HCSA-VM-Linux安装虚拟机后的基础命令 1.代码命令 1.查看本机IP地址: ip addr 或者 ip a [foxbogon ~]$ ip addre [foxbogon ~]$ ip a 1:<Loopback,U,LOWER-UP> 为环回2网卡 2: ens160: <BROADCAST,MULTICAST,UP,LOWER_UP&g…...
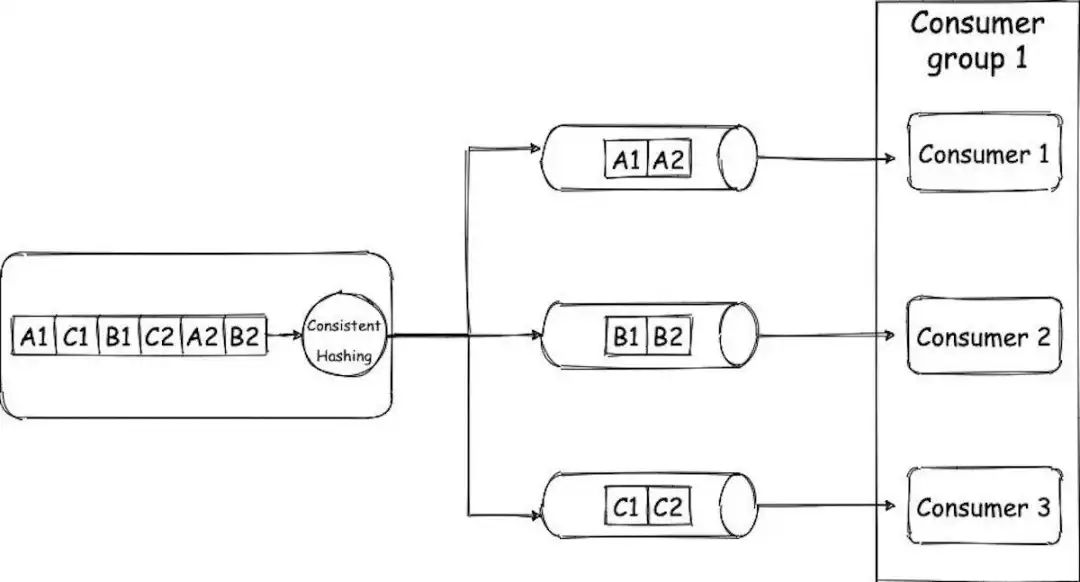
Kafka:介绍和内部工作原理
展示Kafka工作方式的简单架构。 什么是Kafka?为什么我们要使用它?它是消息队列吗? 它是一个分布式流处理平台或分布式提交日志。 Kafka通常用于实时流数据管道,即在系统之间传输数据,构建不断流动的数据转换系统和构…...

在 EMR Serverless 上使用 Delta Lake
本文是一份开箱即用的全自动测试脚本,用于在 EMR Serverless 上提交一个 Delta Lake 作业。本文完全遵循《最佳实践:如何优雅地提交一个 Amazon EMR Serverless 作业?》 一文给出的标准和规范! 1. 导出环境相关变量 注意&#x…...
)
Stream流的使用详解(持续更新)
1. 对比两List集合数据某些字段一样的情况下取值: 一般简单方式我们会使用双重for循环来处理判断数据取值(如下代码所示),但是数据量越大的情况下代码效率则越低,并且现在很多公司都会限制for循环层数所以更推荐strea…...

golang工程——gRpc 拦截器及原理
oauth2认证与拦截器 类似java spring中的拦截器。gRpc也有拦截器的说法,拦截器可作用于客户端请求,服务端请求。对请求进行拦截,进行业务上的一些封装校验等,类似一个中间件的作用 拦截器类型 一元请求拦截器流式请求拦截器链式…...
Python接口自动化之unittest单元测试
以下主要介绍unittest特性、运行流程及实际案例。 一、单元测试三连问 1、什么是单元测试? 按照阶段来分,一般就是单元测试,集成测试,系统测试,验收测试。单元测试是对单个模块、单个类或者单个函数进行测试。 将访…...
在亚马逊云科技Amazon SageMaker上部署构建聊天机器人的开源大语言模型
开源大型语言模型(LLM)已经变得流行起来,研究人员、开发人员和组织都可以使用这些模型来促进创新和实验。这促进了开源社区开展合作,从而为LLM的开发和改进做出贡献。开源LLM提供了模型架构、训练过程和训练数据的透明度ÿ…...

【51单片机】10-蜂鸣器
1.蜂鸣器的原理 这里的“源”不是指电源。而是指震荡源。 也就是说,有源蜂鸣器内部带震荡源,所以只要一通电就会叫。 而无源内部不带震荡源,所以如果用直流信号无法令其鸣叫。必须用2K~5K的方波去驱动它。 有源蜂鸣器往往比无源的贵ÿ…...

26377-2010 逆反射测量仪 知识梳理
声明 本文是学习GB-T 26377-2010 逆反射测量仪. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了逆反射测量仪的术语和定义、结构与分类、技术要求、计量学特性、试验方法、检验规 则以及标志、包装、运输与贮存。 本标准适用于…...
css实现渐变电量效果柱状图
我们通常的做法就是用echarts来实现 比如 echarts象形柱图实现电量效果柱状图 接着我们实现进阶版,增加渐变效果 echarts分割柱形图实现渐变电量效果柱状图 接着是又在渐变的基础上,增加了背景色块的填充 echarts实现渐变电量效果柱状图 其实思路是一…...
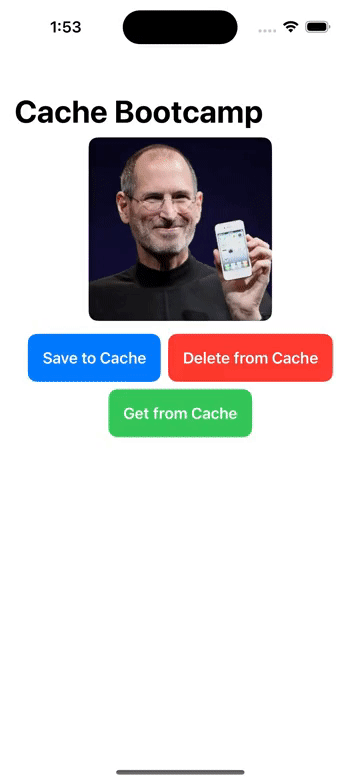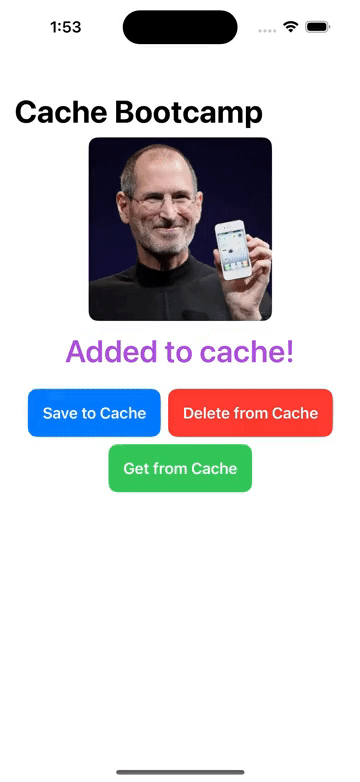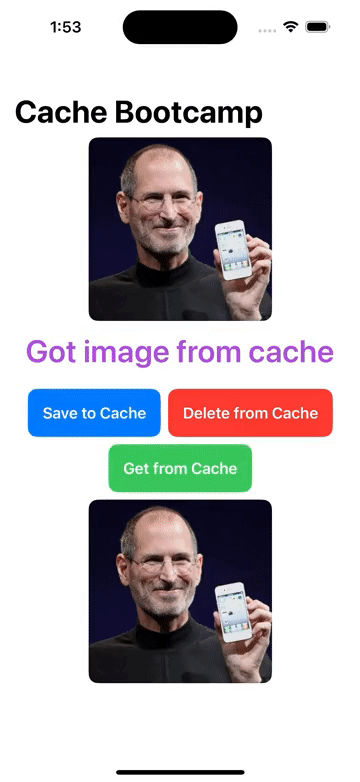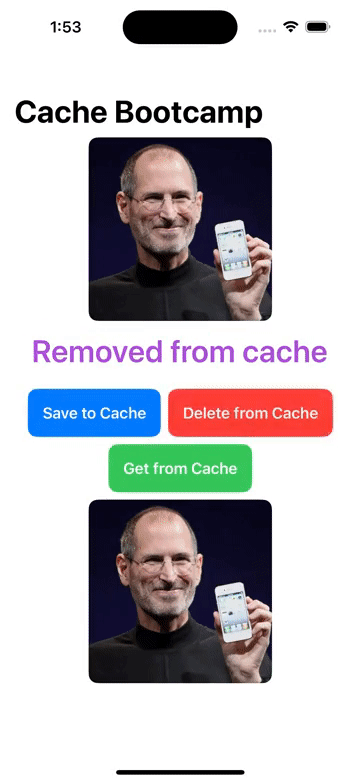
FileManager/本地文件增删改查, Cache/图像缓存处理 的操作
1. FileManager 本地文件管理器,增删改查文件 1.1 实现 // 本地文件管理器 class LocalFileManager{// 单例模式static let instance LocalFileManager()let folderName "MyApp_Images"init() {createFolderIfNeeded()}// 创建特定应用的文件夹func cr…...

vue中使用富文本编辑器
vue中使用富文本编辑器(wangEditor) wangEditor官网地址:https://www.wangeditor.com/ 使用示例 <template><div class"app-container"><div class"box"><div class"editor-tool">&l…...
13.(开发工具篇github)如何在GitHub上上传本地项目
一:创建GitHub账户并安装Git 二:创建一个新的仓库(repository) 三、拉取代码 git clone https://github.com/ainier-max/myboot.git git clone git@github.com:ainier-max/myboot.git四、拷贝代码到拉取后的工程 五、上传代码 (1)添加所有文件到暂存...

vue3中状态适配
写一个函数,在函数中定义一个对象 用于存放键值对,最后返回指定状态所对应的的值,即对象[指定状态] 的 对象的值。 在模板中把状态传入 // vue3 setup语法糖中 const formatXXXState (xxxState)>{const stateMap {键1: 值1,键2: 值2,.…...
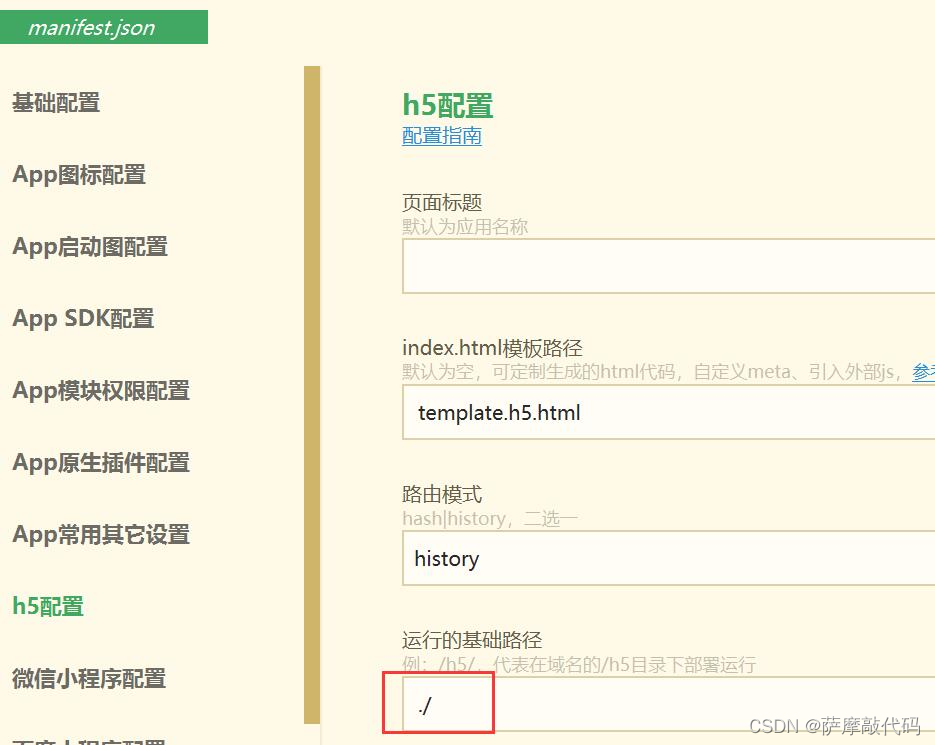
uniapp h5 端 router.base设置history后仍有#号
manifest.json文件设置: "h5": { "router": { "base": "./", "mode": "history" }, }按相对路径发行时路由模式强制为hash模式,不支持history模式(两者相悖)…...

上网行为监管软件(上网行为管理软件通常具有哪些功能)
在我们的日常生活中,互联网已经成为了我们获取信息、交流思想、进行工作和娱乐的重要平台。然而,随着互联网的普及和使用,网络安全问题也日益突出,尤其是个人隐私保护和网络行为的规范。在这个背景下,上网行为审计软件…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...
