编程面试_动态规划
题目1 最大连续乘积子串
题目描述给一个浮点数序列,取最大乘积连续子串的值,例如 -2.5,4,0,3,0.5,8,-1,则取出的最大乘积连续子串为3,0.5,8。也就是说,上述数组中,3 0.5 8这3个数的乘积30.58=12是最大的,而且是连续的。考虑到乘积子序列中有正有负也还可能有0,我们可以把问题简化成这样:数组中找一个子序列,使得它的乘积最大;同时找一个子序列,使得它的乘积最小(负数的情况)。因为虽然我们只要一个最大积,但由于负数的存在,我们同时找这两个乘积做起来反而方便。也就是说,不但记录最大乘积,也要记录最小乘积。假设数组为a[],直接利用动态规划来求解,考虑到可能存在负数的情况,我们用maxend来表示以a[i]结尾的最大连续子串的乘积值,用minend表示以a[i]结尾的最小的子串的乘积值,那么状态转移方程为:maxend = max(max(maxend * a[i], minend * a[i]), a[i]);minend = min(min(maxend * a[i], minend * a[i]), a[i]);初始状态为maxend = minend = a[0]。
参考代码如下:
double MaxProductSubString(double *a, int num){double MaxEnd = a[0];double MinEnd = a[0];double MaxResult = a[0];for(int i = 0; i < num; ++i){double end1 = MaxEnd * a[i], end2 = MinEnd * a[i];MaxEnd = max(max(end1, end2), a[i]);MinEnd = min(min(end1, end2), a[i]);MaxResult = max(MaxResult, MaxEnd);}return MaxResult;}// 动态规划求解的方法一个for循环搞定,所以时间复杂度为O(n)。
搜索算法中的老祖宗,深度和广度优先搜索算法。
广度优先(BFS Breadth-First Search)搜索
这个用形象的比喻,就像是地震波,从起点向外辐射,直到找到目标点。我们在实现的时候,一般采用队列来实现。广搜是一层一层往外遍历,寻找最短路径,其策略是采取队列的方法。这个算法的优点:1、简单。代码也就几十行;2、路径能找到最优解;不足:1、算法消耗的时间比较大,遍历的点会很多。广度优先搜索之所以能找到最优的路径,原因就是:每一次扩展的点,都是距离出发点最近、步骤最少的。如此这样递推,当扩展到目标点的时候,也是距离出发点最近的。这样的路径自然形成了最短的路线。
深度优先(DFS Depth-First Search)搜索
用俗话说就是不见棺材不回头。算法会朝一个方向(目标位置)进发,直到遇到边界或者障碍物,才改变方向。一般在实现的时候,我们采用递归的方式来进行,也可以采用模拟压栈的方式来实现。这个算法的好处就是实现简单,可能就十几行代码。不过问题也很明显,就是:1、路径可能不是最优解;2、寻路时间比较长。
数据结构----BFS和DFS详解 c++代码
A*算法 广度优先 + 启发式搜索 考虑距出发点距离 + 距目标点距离
正是由于广度优先搜索一层层的扩展,虽然让他找到了最优的路线,但是,他却很傻的走完了绝大多数格子,才找到我们的目标点。也就是,他只关注了当前扩展点和出发点的关系,而忽略了当前点和目标点的距离。如果,如果,如果……我们每扩展一个点,就踮起脚尖,看看诗和远方,找找我们要寻找的那个目标,是不是就有可能指引我们快速的去往正确的方向,而不用傻乎乎的一层层的发展了呢?答案是肯定的。A*算法相对广度优先搜索算法,除了考虑中间某个点同出发点的距离以外,还考虑了这个点同目标点的距离。这就是A*算法比广度优先算法智能的地方。也就是所谓的启发式搜索。
如果用f(M)表示:从起点S到终点E(经过M点)的距离,那他就可以表示成为两段距离之和,M为中间策略点
即:S→M的距离 + M→E的距离。如果我们用符号表示的话,就可以写成:f(M) = g(M) + h(M)。 我们扩展到M点的时候,S→M的距离就已经知道,所以g(M)是已知的。但是M到E的距离我们还不知道。如果我们能用某种公式,能大概预测一下这个距离,而这个预测的值又比较精确,我们是不是就能很精确的知道每一个即将扩展的点是否是最优的解路径上的点呢?
估算函数h(M)如何计算?
常见的距离计算公式有这么几种:1、曼哈顿距离:这个名字听起来好高端,说白了,就是上面我们讲的横向格子数+纵向格子数(折线段距离);2、欧式距离:这个名字听起来也很高端,说白了,就是两点间的直线距离sqrt((x1-x2)^2 + (y1-y2)^2)3、欧式距离平方: (x1-x2)^2 + (y1-y2)^2除了上述的距离计算公式以外,还有一些变种的距离计算公式,如:对角线距离等等。这个就在具体的问题中做具体的优化了。
不同估算函数对于结果的影响
1、当估算的距离h完全等于实际距离h'时,也就是每次扩展的那个点我们都准确的知道,如果选他以后,我们的路径距离是多少,这样我们就不用乱选了,每次都选最小的那个,一路下去,肯定就是最优的解,而且基本不用扩展其他的点。2、如果估算距离h小于实际距离h'时,我们到最后一定能找到一条最短路径(如果存在另外一条更短的评估路径,就会选择更小的那个),但是有可能会经过很多无效的点。曼哈顿距离\欧式距离极端情况,当h==0的时候,最终的距离函数就变成:f(M)=g(M)+h(M)=> f(M)=g(M)+0=> f(M)=g(M)这不就是我们的广度优先搜索算法嘛?! 他只考虑和起始点的距离关系,毫无启发而言。 3、如果估算距离h大于实际距离h'时,有可能就很快找到一条通往目的地的路径,但是却不一定是最优的解。这种情况就是h值大于等于实际距离的,明显他扩展的点很少,不过找到的路径却不是最短路径。欧式距离平方
Dijkstra(迪杰斯特拉)算法
算法特点:
迪科斯彻算法使用了 广度优先搜索 BFS
解决 赋权的有向图 或者 无向图的 单源最短路径问题,算法最终得到一个最短路径树。
该算法常用于路由算法或者作为其他图算法的一个子模块。
算法的思路
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点s 到各个顶点m 的最短距离 和一个保存已经找到了最短路径的顶点的集合:T,初始时:原点s 的路径权重被赋为 0 (dis[s] = 0)。若对于顶点 s 存在能直接到达的边(s,m) 另一个顶点为m则把dis[m]设为w(s, m),即单个路径边上的权重值,同时把所有其他(s不能直接到达的)顶点的路径长度设为无穷大。初始时,短路集合T 只有 顶点s。 然后,从dis数组选择最小值,则该值就是 源点s 到该值对应的顶点 m 的最短路径,并且把该点加入到 短路集合T中,OK,此时完成一个顶点, 然后,我们需要看看新加入的顶点是否可以到达其他顶点,并且看看通过该顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。 然后,又从dis中找出最小值,重复上述动作,直到T中包含了图的所有顶点。
示例:
顶点数 边数6 8起点 终点 权重值1 3 101 5 301 6 1002 3 53 4 504 6 105 4 205 6 60图的邻接矩阵为:∞ ∞ 10 ∞ 30 100 v1节点直接到达其他节点的距离∞ ∞ 5 ∞ ∞ ∞∞ ∞ ∞ 50 ∞ ∞∞ ∞ ∞ ∞ ∞ 10 ...∞ ∞ ∞ 20 ∞ 60∞ ∞ ∞ ∞ ∞ ∞ v6节点直接到达其他节点的距离新建dis 向量(从v1到达各个点 经过的最短距离)dis = {0, ∞, 10, ∞, 30, 100}解法:步骤1:v1 到 v3 路径最短 dis[2] = 10, 下标从0开始 除去dis[0]外最小的 为dis[2] 到第三个顶点 v3v3可以到达v4,v1->v3->v4 距离为 10 + 50 = 60而从v1直接到v4,v1->v4,距离为无穷大,dis[3] = 60dis = {0, ∞, 10, 60, 30, 100}因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3],通过 <v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想:通过“边”来松弛v1顶点到其余各个顶点的路程。步骤2:我们从除去 dis[0] 、 dis[2]中选择最小的 为 dis[4] = 30 到第五个顶点 v5v5 可以到达 v4, v1->v5->v4 距离为 30 + 20 = 50,而,从v1->v4为 60 > 50 ,则 dis[3] 被更新为 50另外 v5 也可以到达 v6,而v1 -> v5 -> v6 = 30 + 60 = 90而,从v1 -> v6 为 100则,dis[5] 被更为 90dis = {0, ∞, 10, 50, 30, 90}步骤3:我们再从 除去 dis[0] 、 dis[2]、 dis[4] 中选择最小的为 dis[3] = 50 到第四个顶点 v4而v4 可以到达 v6,v1 -> v4 -> v6 距离为 50 + 10 = 60而v1 -> v6 = 90 > 60 ,则dis[5] 被更新为 60dis = {0, ∞, 10, 50, 30, 60}步骤4:然后,从除去 dis[0] 、 dis[2]、 dis[4]、dis[3] 中选取最小的为 dis[5] = 60 到第六个顶点 v4而 v6 到达不了其他地方,更新不了
Dijkstra算法的代码实现(c++)
Dijkstra.h 头文件的代码
// Dijkstra.h#pragma once//#pragma once是一个比较常用的C/C++杂注,//只要在头文件的最开始加入这条杂注,//就能够保证头文件只被编译一次。#include<iostream>#include<string>using namespace std;/*本程序是使用Dijkstra算法实现求解最短路径的问题采用的邻接矩阵来存储图*///记录起点到每个顶点的最短路径的信息struct Dis {string path;//字符串路径 int value; //最短路径值bool visit; //已经找到最短路径的标记 Dis() { //结构体初始化函数
visit = false;
value = 0;
path = “”;
}
};
// 自定义类的声明
class Graph_DG {
private:// 私有变量
int vexnum; //图的顶点个数 v1,v2,…,v6
int edge; //图的边数
int **arc; //邻接矩阵 二维数组 指针的指针
Dis * dis; //记录各个顶点最短路径的信息
public://共有函数方法 Graph_DG(int vexnum, int edge); // 默认构造函数 与类同名~Graph_DG(); // 销毁时自动执行的析构函数 构造函数前 + ~//顶点从1开始编号 而权重必须大于0 bool check_edge_value(int start, int end, int weight); // 判断我们每次输入的的边的权重信息是否合法void createGraph(); //创建图void print(); //打印邻接矩阵void Dijkstra(int begin); //求最短路径void print_path(int); //打印最短路径};
Dijkstra.cpp 源文件的代码
// Dijkstra.cpp 源文件的代码
#include"Dijkstra.h"// 包含声明 头文件
//默认构造函数Graph_DG::Graph_DG(int vexnum, int edge) {//初始化顶点数和边数this->vexnum = vexnum;this->edge = edge;//为邻接矩阵开辟空间和赋初值arc = new int*[this->vexnum];// 指针数组 顶点数 * 顶点数的 二维数组dis = new Dis[this->vexnum]; // 最短路径 向量for (int i = 0; i < this->vexnum; i++) {arc[i] = new int[this->vexnum];// 行数组for (int k = 0; k < this->vexnum; k++) {arc[i][k] = INT_MAX; //邻接矩阵初始化为无穷大}}}//析构函数Graph_DG::~Graph_DG() {delete[] dis;// delete[] 删除 最短路径 变量 数组for (int i = 0; i < this->vexnum; i++) {delete this->arc[i];// 删除邻接矩阵 每一行的数组}delete arc; // 删除邻接矩阵 数组}// 判断我们每次输入的的边的信息是否合法 权重必须大于0 //顶点从1开始编号bool Graph_DG::check_edge_value(int start, int end, int weight) {if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {return false;}return true;}//创建初始邻接图 根据输入信息void Graph_DG::createGraph() {cout << "请输入每条边的起点和终点(顶点编号从1开始)以及其权重" << endl;int start;int end;int weight;int count = 0;// 输入边数记录while (count != this->edge) {// 0~edge-1cin >> start >> end >> weight;// 得到 起点终点 对应权重//首先判断边的信息是否合法while (!this->check_edge_value(start, end, weight)) {cout << "输入的边的信息不合法,请重新输入" << endl;cin >> start >> end >> weight;}//对邻接矩阵对应上的点赋值arc[start - 1][end - 1] = weight;//无向图添加上这行代码//arc[end - 1][start - 1] = weight;++count;}}// 打印邻接矩阵void Graph_DG::print() {cout << "图的邻接矩阵为:" << endl;int count_row = 0; //打印行的标签int count_col = 0; //打印列的标签//开始打印while (count_row != this->vexnum) {count_col = 0;while (count_col != this->vexnum) {if (arc[count_row][count_col] == INT_MAX)cout << "∞" << " ";elsecout << arc[count_row][count_col] << " ";++count_col;// 列 下标}cout << endl;++count_row;// 行 下标}}// Dijkstra 求最短路径void Graph_DG::Dijkstra(int begin){//【1】首先初始化我们的dis数组int i;for (i = 0; i < this->vexnum; ++i) {//设置当前的路径dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);dis[i].value = arc[begin - 1][i];// v11 v12 v13 v14 v15 v16的值}//设置起点到起点的路径为0dis[begin - 1].value = 0;dis[begin - 1].visit = true;int count = 1;//计算剩余的顶点的最短路径( 剩余this->vexnum-1个顶点)while (count != this->vexnum) {// 【2】找到 dis数组内的最小路径值// temp用于保存当前dis数组中最小的那个下标// min记录的当前的最小值int temp=0;// int min = INT_MAX;for (i = 0; i < this->vexnum; i++) {if (!dis[i].visit && dis[i].value < min) {min = dis[i].value;// 最小值temp = i;// 最小下标}}//cout << temp + 1 << " "<<min << endl;//把temp对应的顶点加入到已经找到的最短路径的集合中dis[temp].visit = true;// 找到标志++count;// 遍历该节点for (i = 0; i < this->vexnum; i++) {//注意这里的条件arc[temp][i]!=INT_MAX必须加,不然会出现溢出,从而造成程序异常if (!dis[i].visit && arc[temp][i] !=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {//如果新得到的边可以影响其他为访问的顶点,那就就更新它的最短路径和长度 v1->v4->v5 < v1->v5 更新dis[i].value = dis[temp].value + arc[temp][i];dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);// 记录路径}}}}//打印最短路径void Graph_DG::print_path(int begin) {string str;str = "v" + to_string(begin);cout << "以"<< str <<"为起点的图的最短路径为:" << endl;for (int i = 0; i != this->vexnum; i++) {if(dis[i].value != INT_MAX)cout << dis[i].path << "=" << dis[i].value << endl;else {cout << dis[i].path << " 是无最短路径的. " << endl;}}}
相关文章:

编程面试_动态规划
题目1 最大连续乘积子串 题目描述给一个浮点数序列,取最大乘积连续子串的值,例如 -2.5,4,0,3,0.5,8,-1,则取出的最大乘积连续子串为3,0.5,8。也就…...

ip地址可以精确定位吗
在互联网时代,IP地址的重要性不言而喻。作为网络通信的基础,IP地址用于标识每一台连接到互联网的设备。然而,传统的IP地址定位方式仅能粗略地确定设备的大致位置,无法实现精确定位。那么,IP地址能否实现精确定位呢&…...

Xamarin体验:使用C#开发iOS/Android应用
http://www.cnblogs.com/lwme/p/use-xamarin-develop-Android-iOS-app.html Xamarin是Mono创始人Miguel de Icaza创建的公司,旨在让开发者可以用C#编写iOS, Android, Mac应用程序,也就是跨平台移动开发。 简介 Xamarin是基于Mono的平台,目前主要有以下产品(更具体请见:h…...

聊聊druid连接池的监控
序 本文主要研究一下druid连接池的监控 init com/alibaba/druid/pool/DruidDataSource.java public void init() throws SQLException {//......registerMbean();//...... }DruidDataSource的init方法会执行registerMbean registerMbean com/alibaba/druid/pool/DruidData…...

CentOS 7 安装 Docker 的详细步骤
文章目录 Docker简介1.更新2.安装必要的软件包3.添加Docker仓库4.安装5.安装后的一些常规设置及常用的命令5.1 启动 Docker5.2 Docker 在系统启动时自动运行5.3 运行一个 Hello World 镜像5.4 查看docker运行状态5.5 docker ps5.6 查看docker版本 6.安装种常见的错误错误1:yum-…...

竞赛 基于深度学习的动物识别 - 卷积神经网络 机器视觉 图像识别
文章目录 0 前言1 背景2 算法原理2.1 动物识别方法概况2.2 常用的网络模型2.2.1 B-CNN2.2.2 SSD 3 SSD动物目标检测流程4 实现效果5 部分相关代码5.1 数据预处理5.2 构建卷积神经网络5.3 tensorflow计算图可视化5.4 网络模型训练5.5 对猫狗图像进行2分类 6 最后 0 前言 &#…...
数据结构之【泛型】
泛型:定义阶段不明确具体类型,产生对象时明确具体类型。 //Object是Java中的最高参数统一化,能够接受所有的引用类型; //有了包装类的自动拆装箱之后,Object还能够接收基本类型数值(自动装箱) …...

华为ac无线侧命令行配置思路和步骤
无线侧配置思路: Ap和ac在同一个广播域内,不用配置 option 43 source 源ip回包哪个模式都得配置 Cli配置业务模版流程: 1、 AC控制器上全局配置capwap回包接口地址 1、配置ssid:wifi名称 2、配置安全模版:用户连接密码…...
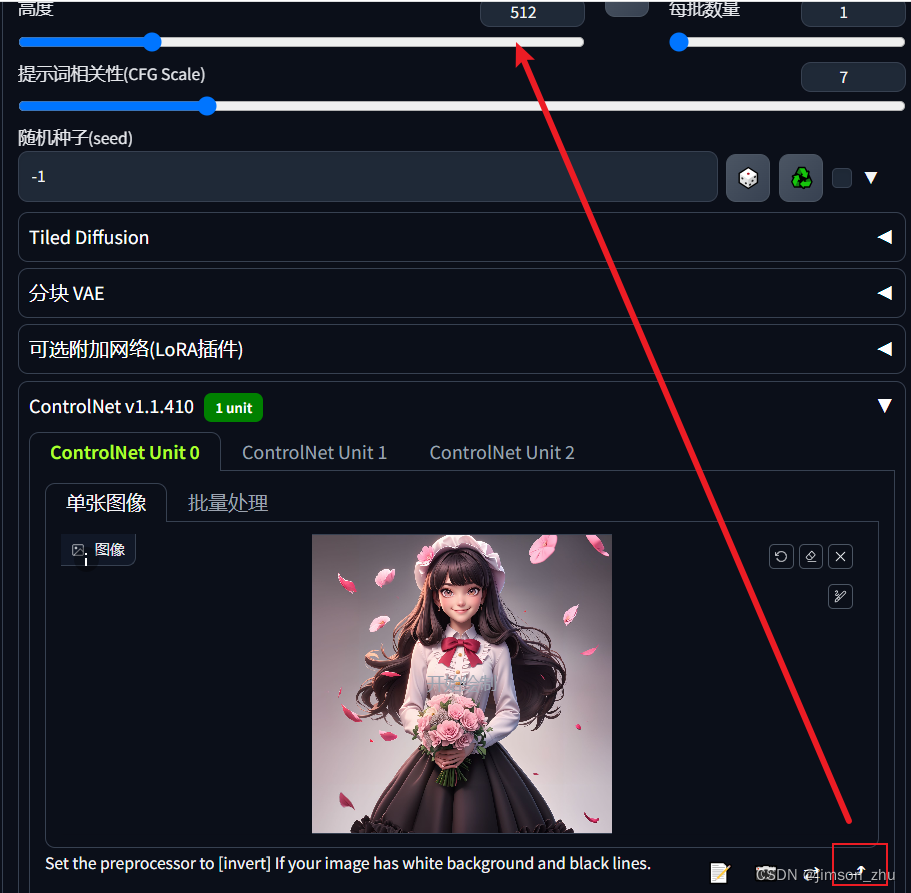
十六)Stable Diffusion教程:出图流程化
今天说一个流程化出图的案例,适用很多方面。 1、得到线稿,自己画或者图生图加线稿lora出线稿;如果想sd出图调整参数不那么频繁细致,则线稿的素描关系、层次、精深要表现出来,表现清楚。 2、文生图,seed随机…...
SpringBoot全局异常处理源码
SpringBoot全局异常处理源码 一、SpringMVC执行流程二、SpringBoot源码跟踪三、自定义优雅的全局异常处理脚手架starter自定义异常国际化引入封装基础异常封装基础异常扫描器,并注册到ExceptionHandler中项目分享以及改进点 一、SpringMVC执行流程 今天这里叙述的全…...

设计模式——7. 装饰者模式
1. 说明 装饰者模式(Decorator Pattern)是一种结构型设计模式,它允许你在不改变对象接口的前提下,动态地将新行为附加到对象上。这种模式是通过创建一个包装(或装饰)对象,将要被装饰的对象包裹起来,从而实现对原有对象功能的增强和扩展。 装饰者模式的主要特点包括:…...
安卓玩机-----反编译apk 修改apk 去广告 去弹窗等操作中的一些常识
安卓机型app的编译与反编译 apk文件的简单说明与解析 -安卓修改apk apk的组成和编译 一 电脑端几种反编译apk工具操作步骤解析 前面几个博文有说明关于反编译apk和apk架构等有些常识.今天对以上做个补充。初学者记住一点。对于一个apk文件使用压缩软件7zip打开可以查看到文件…...

Hoeffing不等式
在李航老师的统计学习方法(第一版中) H o e f f i n g 不等式 Hoeffing不等式 Hoeffing不等式是这样子给出的 设 X 1 , X 2 , . . . , X N X_1,X_2,...,X_N X1,X2,...,XN是独立随机变量,且 X i ∈ [ a i , b i ] , i 1 , 2 , . . . ,…...

ffmpeg解复用指定pid转推udp
命令 ffmpeg -re -i udp://224.2.2.2:4003?fifo_size1024000 -map #5001 -acodec copy -flush_packets 1 -f mpegts udp://192.168.2.62:5161 ffmpeg -re -i udp://224.2.2.2:4003?fifo_size1024000 -map #5001 -acodec copy -flush_packets 1 -f mpegts udp://192.16…...
Vue组件通信方式
1.props通信 1.1在 Vue 2 中使用 props 通信 注意:props传递的数据是只读的,子组件修改,不会影响父组件 1.1.1.定义 props 在子组件中使用 props 选项来定义要接收的属性 // 子组件 <script> export default {props: {message: String} } </script>1.1.2.传递…...
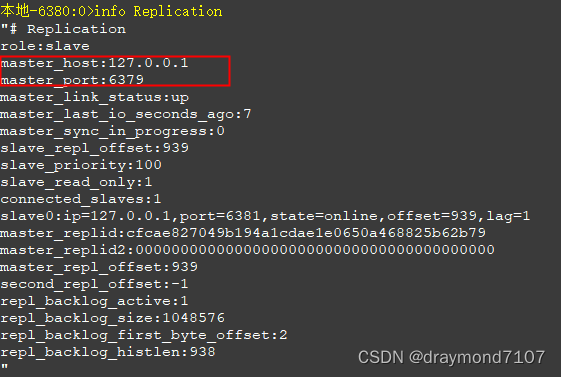
redis-设置从节点
节点结构 节点配置文件 主节点 不变 6380节点 port 6380 slaveof 127.0.0.1 63796381节点 port 6381 slaveof 127.0.0.1 6380启动 指定配置文件的方式启动 D:\jiqun\redis\Redis-6380>redis-server.exe redis.windows.conf启动时,会触发同步数据命令 主节点…...

k8s-实战——基于nfs实现动态存储
部署nfs服务 基于Centos7.9版本创建动态存储注意k8s版本应低于v1.24版本高k8s版本ServiceAccount需要手动创建secrets并关联相关sa部署流程 创建NFS共享服务、采用单独的节点用于nfs服务独占安装nfs-utils和rpcbindnfs客户端和服务端都安装nfs-utils包通过部署化脚本安装k8s集群…...

【广州华锐互动】鱼类授精繁殖VR虚拟仿真实训系统
随着科技的不断发展,虚拟现实技术在各个领域的应用越来越广泛。在养殖业中,VR技术可以帮助养殖户进行家鱼授精实操演练,提高养殖效率和繁殖成功率。本文将介绍利用VR开展家鱼授精实操演练的方法和应用。 首先,我们需要了解家鱼授精…...
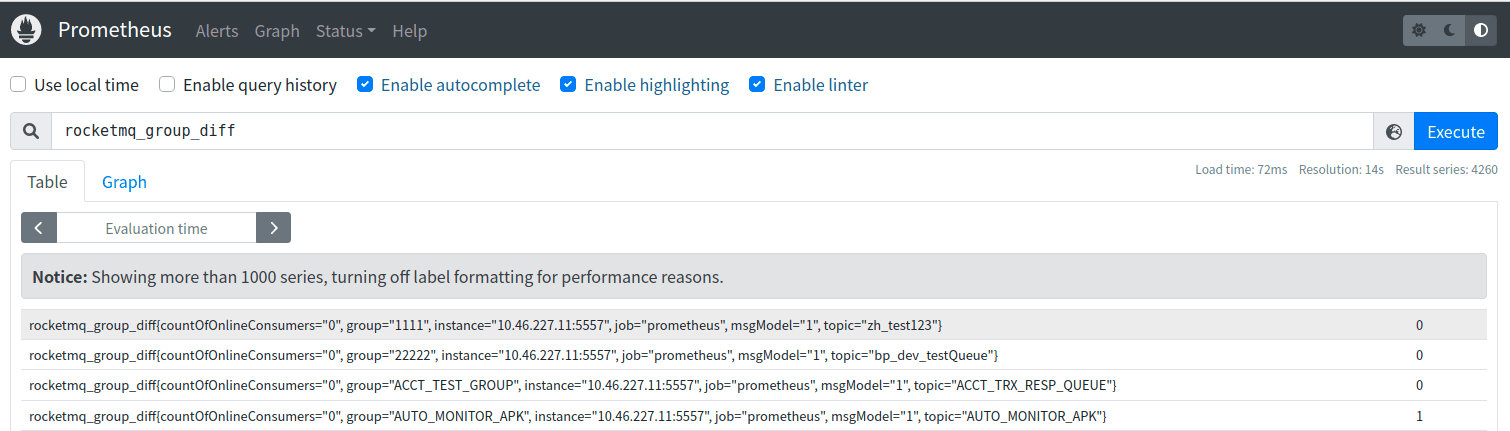
RocketMQ Promethus Exporter
介绍 Rocketmq-exporter 是用于监控 RocketMQ broker 端和客户端所有相关指标的系统,通过 mqAdmin 从 broker 端获取指标值后封装成 87 个 cache。 警告 过去版本曾是 87 个 concurrentHashMap,由于 Map 不会删除过期指标,所以一旦有 la…...

Kafka收发消息核心参数详解
文章目录 1、从基础的客户端说起1.1、消息发送者主流程1.2、消息消费者主流程 2、从客户端属性来梳理客户端工作机制2.1、消费者分组消费机制 1、从基础的客户端说起 Kafka提供了非常简单的客户端API。只需要引入一个Maven依赖即可: <dependency><groupId…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
