使用LDA(线性判别公式)进行iris鸢尾花的分类
线性判别分析((Linear Discriminant Analysis ,简称 LDA)是一种经典的线性学习方法,在二分类问题上因为最早由 [Fisher,1936] 提出,亦称 ”Fisher 判别分析“。并且LDA也是一种监督学习的降维技术,也就是说它的数据集的每个样本都有类别输出。这点与主成分和因子分析不同,因为它们是不考虑样本类别的无监督降维技术。
LDA 的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同样样例的投影尽可能接近、异样样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定新样本的类别。其实可以用一句话概括:就是“投影后类内方差最小,类间方差最大”。
鸢尾花简介
iris数据集的中文名是安德森鸢尾花卉数据集,英文全称是Anderson’s Iris data set。iris包含150个样本,对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息,所以iris数据集是一个150行5列的二维表。
通俗地说,iris数据集是用来给花做分类的数据集,每个样本包含了花萼长度、花萼宽度、花瓣长度、花瓣宽度四个特征(前4列),我们需要建立一个分类器,分类器可以通过样本的四个特征来判断样本属于山鸢尾、变色鸢尾还是维吉尼亚鸢尾(这三个名词都是花的品种)。
iris的每个样本都包含了品种信息,即目标属性(第5列,也叫target或label)。
代码
#首先导入相关库
import sklearn
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt#再进行数据的划分
data = load_iris(return_X_y=True)
x,y = data
#print(x)
#print(y)
#分割训练集和测试集
train_x,test_x,train_y,test_y = train_test_split(x,y,test_size=0.3)
print(train_x.shape)
print(test_x.shape)#进行训练
LDA = LinearDiscriminantAnalysis()
LDA.fit(train_x,train_y)
y_predict = LDA.predict(test_x)
print(test_y)
print(y_predict)相关输出如下
[2 1 2 1 0 2 2 0 2 0 1 2 1 0 1 0 0 0 0 2 2 1 2 1 0 1 1 2 2 0 2 1 2 0 2 1 21 0 2 0 0 1 0 2] [2 1 2 1 0 2 2 0 2 0 1 2 1 0 1 0 0 0 0 2 2 1 2 1 0 1 1 2 2 0 2 1 2 0 2 1 21 0 2 0 0 1 0 2]
#计算预测正确率
j = 0
for i in range(len(test_y)):if test_y[i] == y_predict[i]:j = j + 1
print(j)
print(j/len(y_predict))画图部分
#由于是按照萼片长度宽度计算,所以将萼片长宽与相应的类别组合成新的列表
total_sepal = []
for i in range(x.shape[0]):sepal = []sepal.append(x[i][0])sepal.append(x[i][1])sepal.append(y[i])total_sepal.append(sepal)
print(total_sepal)#画图
for i in range(x.shape[0]):if(total_sepal[i][2] == 0):plt.scatter(total_sepal[i][0], total_sepal[i][1], color='blue')if(total_sepal[i][2] == 1):plt.scatter(total_sepal[i][0], total_sepal[i][1], color='red')if(total_sepal[i][2] == 2):plt.scatter(total_sepal[i][0], total_sepal[i][1], color='green')
plt.show()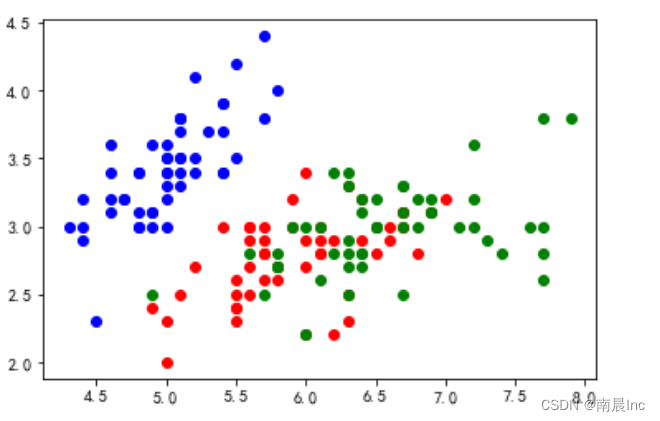
相关文章:

使用LDA(线性判别公式)进行iris鸢尾花的分类
线性判别分析((Linear Discriminant Analysis ,简称 LDA)是一种经典的线性学习方法,在二分类问题上因为最早由 [Fisher,1936] 提出,亦称 ”Fisher 判别分析“。并且LDA也是一种监督学习的降维技术,也就是说它的数据集的每个样本都…...

王学岗生成泛型的简易Builder
github大佬地址 使用 //class 可以传参DataBean.classpublic static <T> T handlerJson(String json, Class<T> tClass) {T resultData null;if (CommonUtils.StringNotNull(json) && !nullString.equals(json)) {if (isArray(json)) {resultData BaseN…...

kafka消息队列简单使用
下面是使用Spring Boot和Kafka实现消息队列的简单例子: 引入依赖 在pom.xml中添加以下依赖: <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId><version>2.7.5&l…...

性能优化实战使用CountDownLatch
1.分析问题 原程序是分页查询EventAffinityScoreDO表的数据,每次获取2000条在一个个遍历去更新EventAffinityScoreDO表的数据。但是这样耗时比较慢,测试过30万的数据需要2小时 private void eventSubjectHandle(String tenantId, String eventSubject) …...
基于视频技术与AI检测算法的体育场馆远程视频智能化监控方案
一、方案背景 近年来,随着居民体育运动意识的增强,体育场馆成为居民体育锻炼的重要场所。但使用场馆内的器材时,可能发生受伤意外,甚至牵扯责任赔偿纠纷问题。同时,物品丢失、人力巡逻成本问题突出,体育场…...
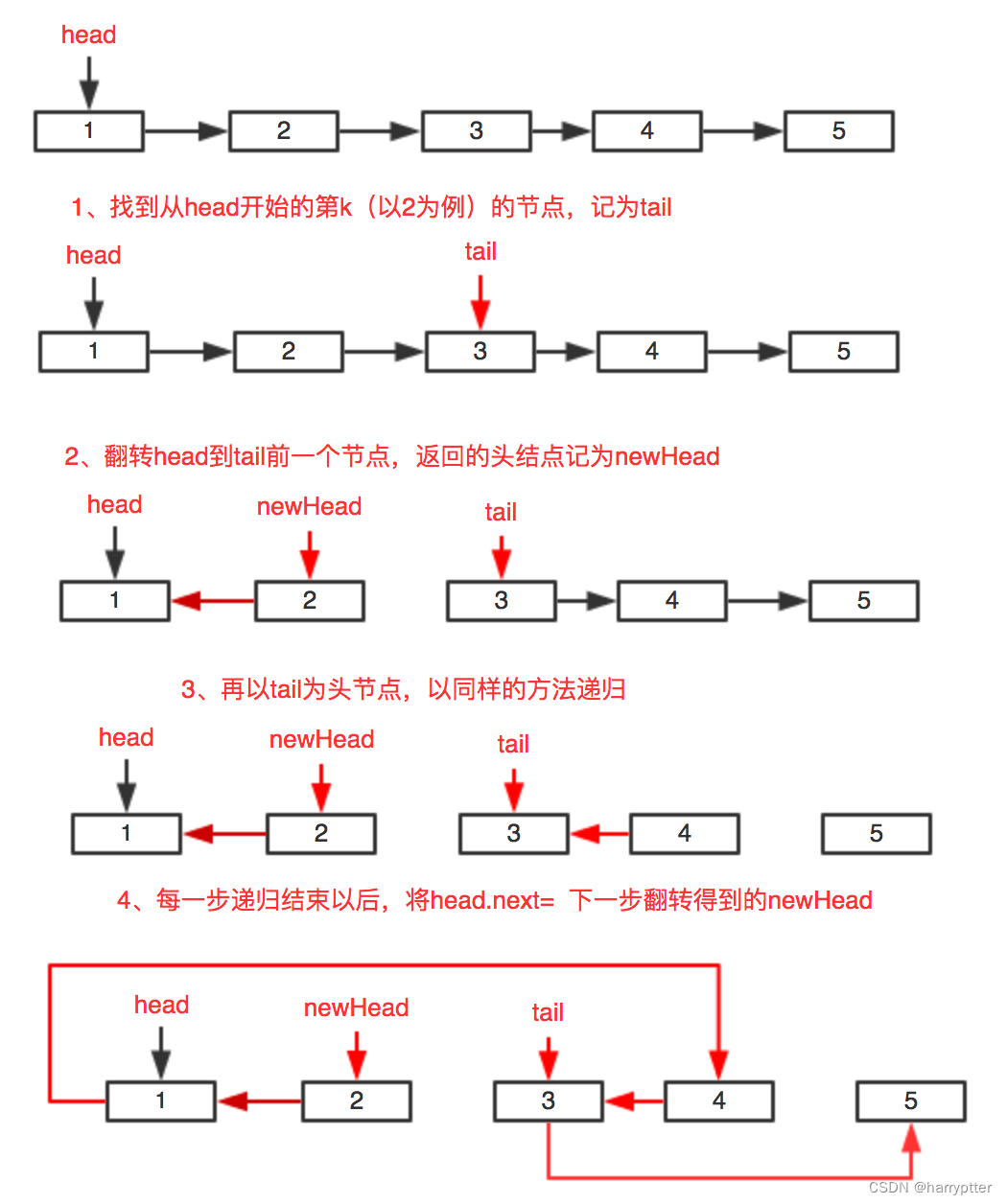
leetcodetop100(29) K 个一组翻转链表
K 个一组翻转链表 给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。 k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。 你不能只是单纯的改…...
最新影视视频微信小程序源码-带支付和采集功能/微信小程序影视源码PHP(更新)
源码简介: 这个影视视频微信小程序源码,新更新的,它还带支付和采集功能,作为微信小程序影视源码,它可以为用户 提供丰富的影视资源,包括电影、电视剧、综艺节目等。 这个小程序影视源码,还带有…...

C++:vector 定义,用法,作用,注意点
C 中的 vector 是标准模板库(STL)提供的一种动态数组容器,它提供了一组强大的方法来管理和操作可变大小的数组。以下是关于 vector 的定义、用法、作用以及一些注意点: 定义: 要使用 vector,首先需要包含 …...
Firecamp2.7.1exe安装与工具调试向后端发送SocketIO请求
背景: 笔者在python使用socket-io包时需要一个测试工具,选择了firecamp这个测试工具来发送请求。 参考视频与exe资源包: Firecamp2.7.1exe安装包以及基本使用说明文档(以SocketIO为例).zip资源-CSDN文库 15_send方法…...
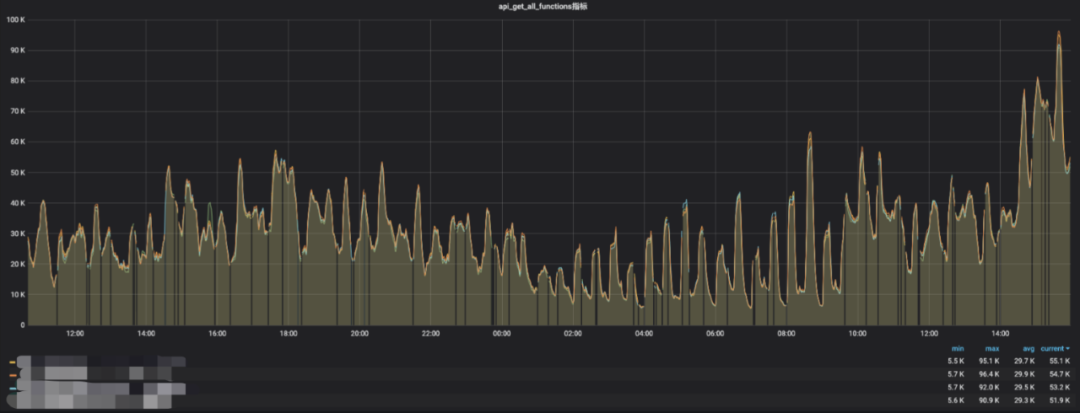
MySQL到TiDB:Hive Metastore横向扩展之路
作者:vivo 互联网大数据团队 - Wang Zhiwen 本文介绍了vivo在大数据元数据服务横向扩展道路上的探索历程,由实际面临的问题出发,对当前主流的横向扩展方案进行了调研及对比测试,通过多方面对比数据择优选择TiDB方案。其次分享了整…...

算法通关村-----寻找祖先问题
最近公共祖先 问题描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一…...
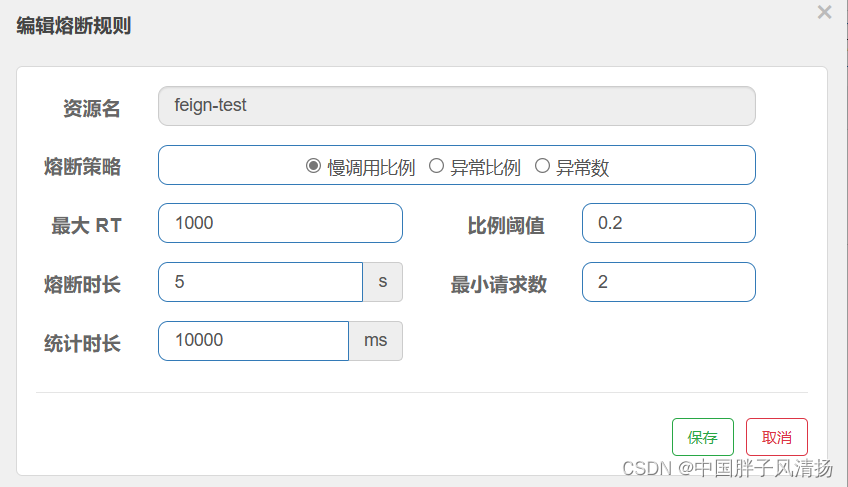
Sentinel结合Nacos实现配置持久化(全面)
1、前言 我们在进行分布式系统的开发中,无论是在开发环境还是发布环境,配置一定不能是内存形式的,因为系统可能会在中途宕机或者重启,所以如果放在内存中,那么配置在服务停到就是就会消失,那么此时就需要重…...

Verilog中什么是断言?
断言就是在我们的程序中插入一句代码,这句代码只有仿真的时候才会生效,这段代码的作用是帮助我们判断某个条件是否满足(例如某个数据是否超出了范围),如果条件不满足(数据超出了范围)࿰…...

Oracle分区的使用详解:创建、修改和删除分区,处理分区已满或不存在的插入数据,以及分区历史数据与近期数据的操作指南
一、前言 什么是表分区: Oracle的分区是一种将表或索引数据分割为更小、更易管理的部分的技术。它可以提高查询性能、简化维护操作,并提供更好的数据组织和管理。 表分区和表空间的区别和联系: 在Oracle数据库中,表空间(Tablespace)是用于存储表、索引和其他数据库对…...
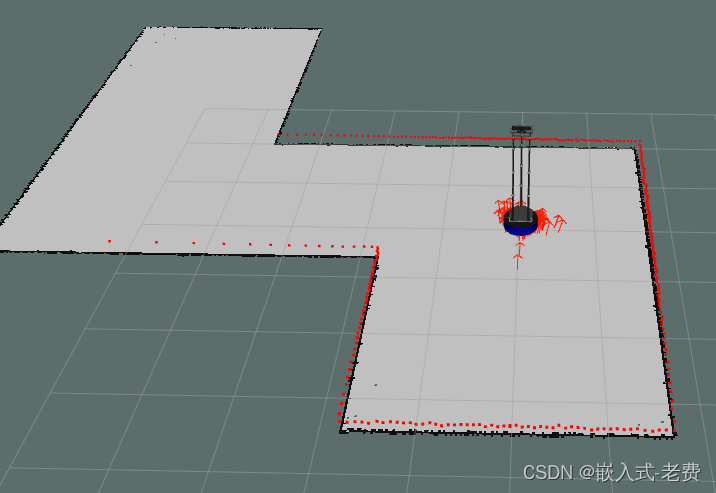
SLAM从入门到精通(amcl定位使用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 学习slam,一般就是所谓的边定位、边制图的知识。然而在实际生产过程中,比如扫地机器人、agv、巡检机器人、农业机器人&…...
【C/C++】C/C++面试八股
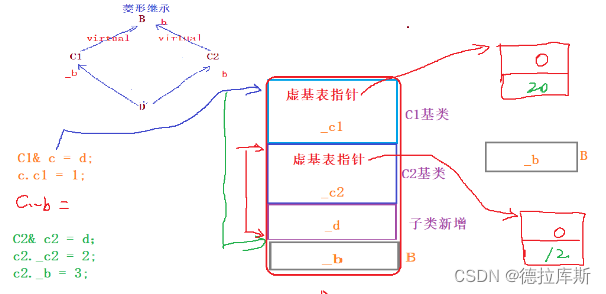
C/C面试八股 C和C语言的区别简单介绍一下三大特性多态的实现原理虚函数的构成原理虚函数的调用原理虚表指针在什么地方进行初始化的?构造函数为什么不能是虚函数虚函数和纯虚函数的区别抽象类类对象的对象模型内存对齐是什么?为什么要内存对齐static关键…...

Scala第八章节
Scala第八章节 scala总目录 章节目标 能够使用trait独立完成适配器, 模板方法, 职责链设计模式能够独立叙述trait的构造机制能够了解trait继承class的写法能够独立完成程序员案例 1. 特质入门 1.1 概述 有些时候, 我们会遇到一些特定的需求, 即: 在不影响当前继承体系的情…...

k8s-实战——kubeadm二进制编译
文章目录 源码编译获取源码修改证书有效期修改 CA 有效期为 100 年(默认为 10 年)修改证书有效期为 100 年(默认为 1 年)CentOS7.9环境准备centos脚本安装执行脚本脚本内容手动安装验证编译查看编译后的版本信息参考链接脚本修改源码编译 源码编译kubeadm文件、修改证书的默…...

vite 和 webpack 的区别
1. 构建原理: Webpack 是一个静态模块打包器,通过对项目中的JavaScript、css、Image 等文件进行分析,生成对应的静态资源,并且通过一些插件和加载器来实现各种功能。 Vite 是一种基于浏览器元素 ES 模块解析构建工具,…...

传统遗产与技术相遇,古彝文的数字化与保护
古彝文是中国彝族的传统文字,具有悠久的历史和文化价值。然而,由于古彝文的形状复杂且没有标准化的字符集,对其进行文字识别一直是一项具有挑战性的任务。本文介绍了古彝文合合信息的文字识别技术,旨在提高古彝文的自动识别准确性…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
