排序篇(一)----插入排序
1.直接插入排序
插入排序的思想:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
你可以想像成打牌一样,比如说斗地主,一张一张的摸牌,然后把手上的这些牌变成手续的排列.
具体步骤如下:
-
将第一个元素视为已排序的序列,将第二个元素与已排序序列进行比较,找到合适的位置插入。
-
将第三个元素与已排序序列进行比较,找到合适的位置插入。
-
以此类推,将后续的元素与已排序序列进行比较并插入。
-
最终得到一个完整的有序序列。
假设现在有一组数据需要排序:
初始序列:5 2 4 6 1 3
-
将第一个元素5视为已排序序列,不需要进行比较,直接插入。
已排序序列:5
未排序序列:2 4 6 1 3
-
将第二个元素2与已排序序列进行比较,找到合适的位置插入。
已排序序列:2 5
未排序序列:4 6 1 3
-
将第三个元素4与已排序序列进行比较,找到合适的位置插入。
已排序序列:2 4 5
未排序序列:6 1 3
-
将第四个元素6与已排序序列进行比较,找到合适的位置插入。
已排序序列:2 4 5 6
未排序序列:1 3
-
将第五个元素1与已排序序列进行比较,找到合适的位置插入。
已排序序列:1 2 4 5 6
未排序序列:3
-
将最后一个元素3与已排序序列进行比较,找到合适的位置插入。
已排序序列:1 2 3 4 5 6
未排序序列:空
最终得到有序序列:1 2 3 4 5 6
int arr[] = { 5, 2, 4, 6, 1, 3};
InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
//直接插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}-
外部循环从第一个元素迭代到倒数第二个元素。
-
在每次迭代中,定义一个变量end,它的初始值为当前外部循环的索引i。
-
定义一个变量tmp,用于存储下一个待插入的元素,即a[end+1]。
-
在内部循环中,从end开始向前遍历数组,比较tmp与当前元素a[end]的大小。
-
如果tmp小于a[end],则将a[end]向后移动一位,即a[end+1] = a[end],并将end减1。
-
重复步骤4和步骤5,直到找到tmp应该插入的位置,即tmp大于等于a[end]。
-
将tmp插入到正确的位置,即a[end+1] = tmp。
-
重复步骤1到步骤7,直到所有元素都被排序。
2.希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:
先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
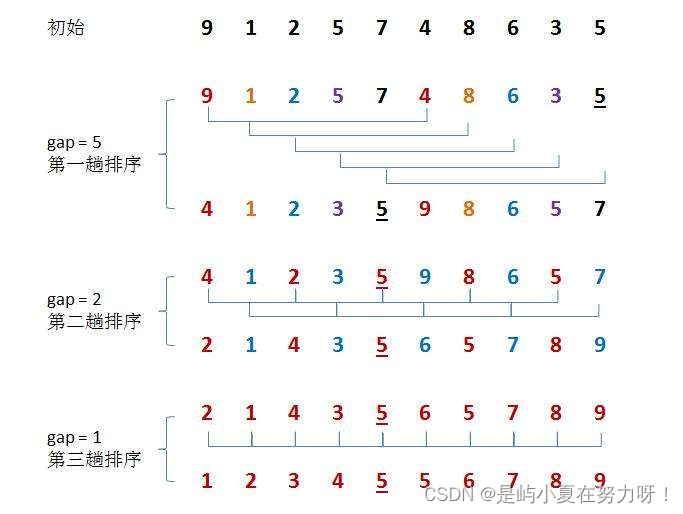
希尔排序的特性总结:
-
希尔排序是对直接插入排序的优化。
-
当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
-
希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
4.希尔排序的时间复杂度都不固定:


我们这里的gap是按照Knuth提出的方式取值的,而且Knuth进行了大量的试验统计,我们暂时就按 照: O(N^1.3)来算.
简而言之希尔排序就是在上面的直接插入排序上加入了预排序,巧妙的就是当gap为1的时候,其实走的就是直接插入排序,可以说希尔排序是直接插入排序的升级版本.
//希尔排序(便于理解版)
void ShellSort1(int* a, int n)
{int gap = n;while (gap > 1){//gap /= 2;gap = gap / 3 + 1;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}
//希尔排序(少一层循环版)
void ShellSort2(int* a, int n)
{int gap = n;while (gap > 1){//gap /= 2;gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}
}代码详解:
ShellSort1版本的希尔排序算法:
-
首先,初始化一个间隔值gap为数组的长度n。
-
在一个循环中,当间隔值大于1时,执行以下操作: a. 将间隔值gap除以3并加1,得到新的间隔值gap。 b. 在一个嵌套循环中,从0到gap-1,对每个间隔进行插入排序:
-
从当前间隔值的位置开始,向后遍历数组,每次以间隔值gap递增。
-
对于每个位置i,将其作为插入排序的起始位置,将a[i+gap]作为待插入的元素tmp。
-
在内部循环中,从当前位置向前遍历,比较tmp与当前元素a[end]的大小。
-
如果tmp小于a[end],则将a[end+gap]的值更新为a[end],并将end减去间隔值gap。
-
如果tmp大于等于a[end],则跳出内部循环。
-
将tmp插入到正确的位置,即a[end+gap] = tmp。
-
-
重复步骤2,直到间隔值gap为1,完成整个排序过程。
ShellSort2版本的希尔排序算法:
-
首先,初始化一个间隔值gap为数组的长度n。
-
在一个循环中,当间隔值大于1时,执行以下操作: a. 将间隔值gap除以3并加1,得到新的间隔值gap。 b. 在一个嵌套循环中,从0到n-gap-1,对每个间隔进行插入排序:
-
从当前位置i开始,将其作为插入排序的起始位置,将a[i+gap]作为待插入的元素tmp。
-
在内部循环中,从当前位置向前遍历,比较tmp与当前元素a[end]的大小。
-
如果tmp小于a[end],则将a[end+gap]的值更新为a[end],并将end减去间隔值gap。
-
如果tmp大于等于a[end],则跳出内部循环。
-
将tmp插入到正确的位置,即a[end+gap] = tmp。
-
-
重复步骤2,直到间隔值gap为1,完成整个排序过程。
这两个版本的希尔排序算法的区别在于内部循环的起始位置不同,ShellSort1从j开始,每次以间隔值gap递增,而ShellSort2从0开始,每次以1递增。
相关文章:

排序篇(一)----插入排序
1.直接插入排序 插入排序的思想: 把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。 你可以想像成打牌一样,比如说斗地主,一张一张的摸牌,然后把手上的这些牌变成手续的排列.…...
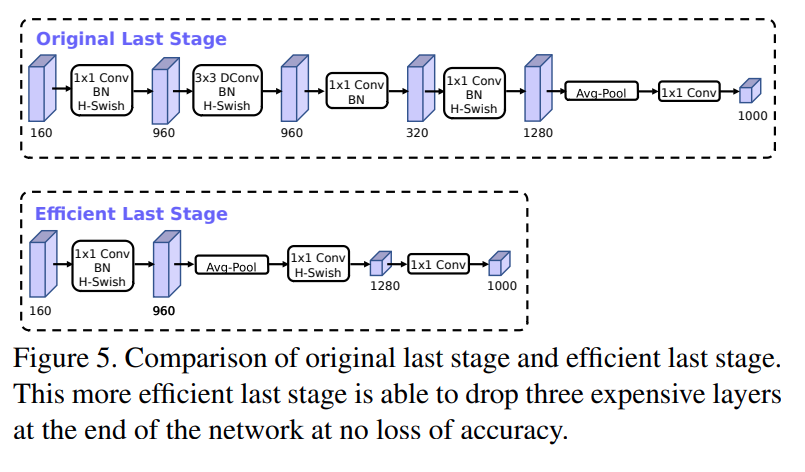
通俗讲解深度学习轻量网络MobileNet-v1/v2/v3
MobileNet网络是由google团队在2017年提出的,专注于移动端或者嵌入式设备中的轻量级CNN网络。相比传统卷积神经网络,在准确率小幅降低的前提下大大减少模型参数与运算量。(相比VGG16准确率减少了0.9%,但模型参数只有VGG的1/32)。MobileNet网络…...

mmpretrain学习笔记
深度学习模型的训练涉及几个方面 1、模型结构:模型有几层、每层多少通道数等 2、数据:数据集划分、数据文件路径、批大小、数据增强策略等 3、训练优化 :梯度下降算法、学习率参数、训练总轮次、学习率变化策略等 4、运行时:GPU、…...

rhel8 网络操作学习
一、查询dns服务器地址汇总 1.查询dns服务器地址: (1)方法一:执行命令 cat /etc/resolv.conf 执行结果如下: nameserver后面就是dns服务器的ip地址。 (2)方法2:查看/etc/syscon…...
,车厂(CarFactory),经销商(Distributor)三个表)
有车型(CarModel),车厂(CarFactory),经销商(Distributor)三个表
用drf编写 1 有车型(CarModel),车厂(CarFactory),经销商(Distributor)三个表, 一个车厂可以生产多种车型,一个经销商可以出售多种车型,一个车型可以有多个经销商出售车型:车型名,车型…...
Python函数:chr()和ord()
两个函数是基于Unicode编码表进行进行字符与字码之间的转换。 chr()函数是通过字码转换成字符: 如图,坐标(1,4e10)丑 使用chr需要线将坐标相加得到:4e11 chr默认传入10进制的字码. 如图是各进制的字码。 也可以传入其他进制,不过需要在前面传入的参数最前…...

flink sql 使用
1.准备工作 安装flink 1.16.2 将以下jar包放到/data/cmpt/flink-1.16.2/lib 目录下 antlr-runtime-3.5.2.jar flink-connector-hive_2.12-1.16.2.jar flink-connector-jdbc-1.16.2.jar mysql-connector-java-6.0.6.jar hive-exec-3.1.3.jar libfb303-0.9.3.ja…...

面试官:谈谈 Go 泛型编程
大家好,我是木川 泛型编程是一种编程范式,它允许编写具有参数化类型的代码,从而增加代码的复用性和灵活性。在泛型编程中,你可以编写一段代码,使其适用于不同类型的参数,而不需要为每种类型编写不同的实现。…...

脚手架开发流程详解
开发流程 创建npm项目创建脚手架入口文件,最上方添加 #!/usr/bin/env/ node配置package.json,添加bin属性编写脚手架代码将脚手架发布到npm 使用流程 安装脚手架 npm install -g your-own-cli使用脚手架 your-own-cli脚手架开发难点解析 分包&…...
)
架构真题2021(四十三)
产品配置是指一个产品在其生命周期各个阶段所产生的各种形式(机器刻可读或人工可读)和各种版本()的集合。 需求规格说明、设计说明、测试报告需求规则说明、设计说明、计算机程序设计说明、用户手册、计算机程序文档、计算机程序…...
数据统计和分析怎么做?spss如何做好数据分析?
为什么要做数据分析?数据分析有什么意义?数据分析可以为企业和组织提供多方面的帮助,包括提高工作效率、优化业务流程、升职加薪、提高管理效率以及改进汇报效果等方面。 IBM SPSS Statistics 26是一款功能强大的统计分析软件,适用于Mac操作…...

【多线程】线程安全的集合类
文章目录 1. 多线程环境使用ArrayList1.1 自己使用同步机制1.2 Collections.synchronizedList(new ArrayList);1.3 使用 CopyOnWriteArrayList 2. 多线程使用队列3. 多线程环境使用哈希表3.1 HashTable3.2 ConcurrentHashMap3.3 Hashtable和HashMap、ConcurrentHashMap 之间的区…...
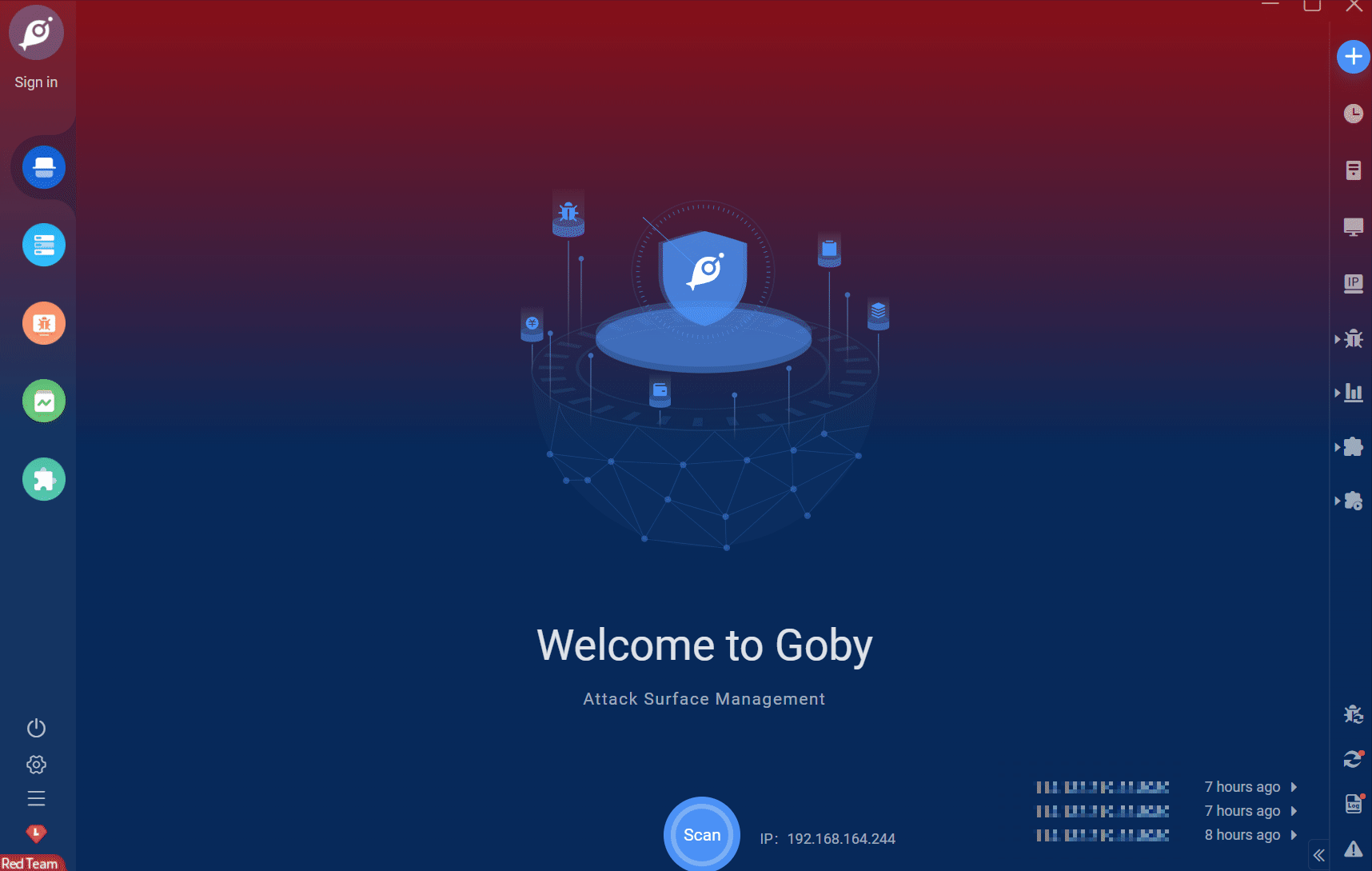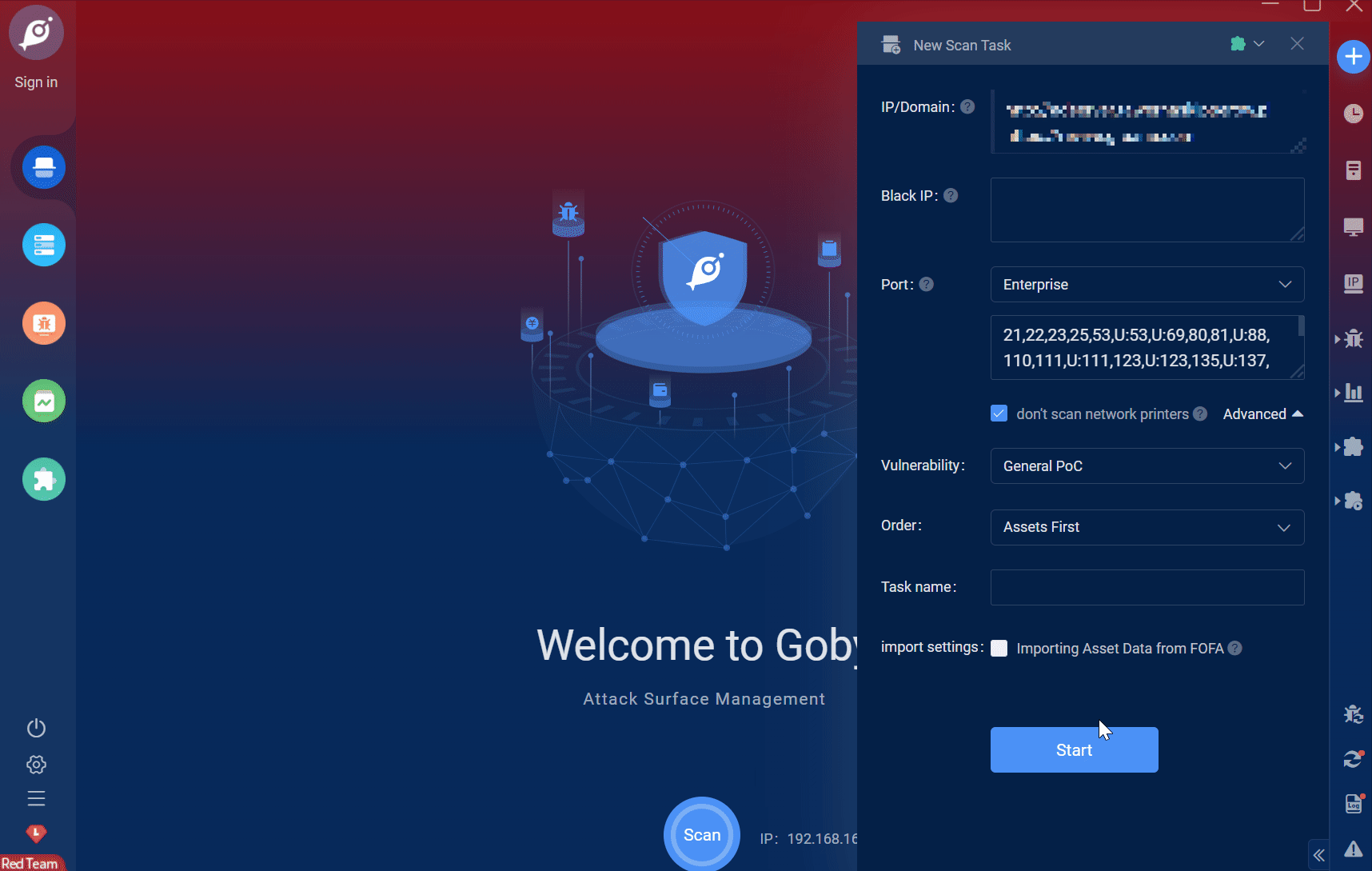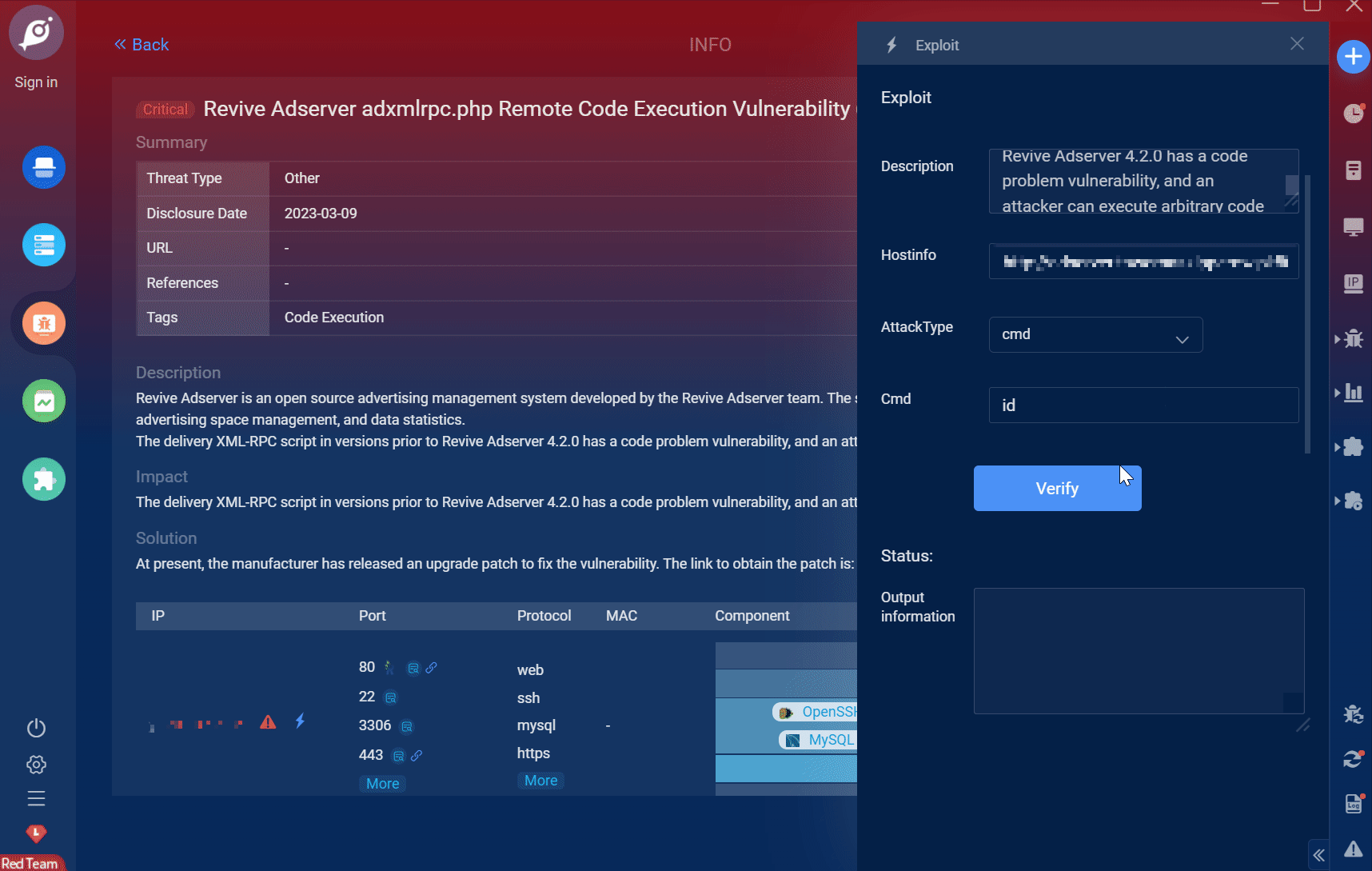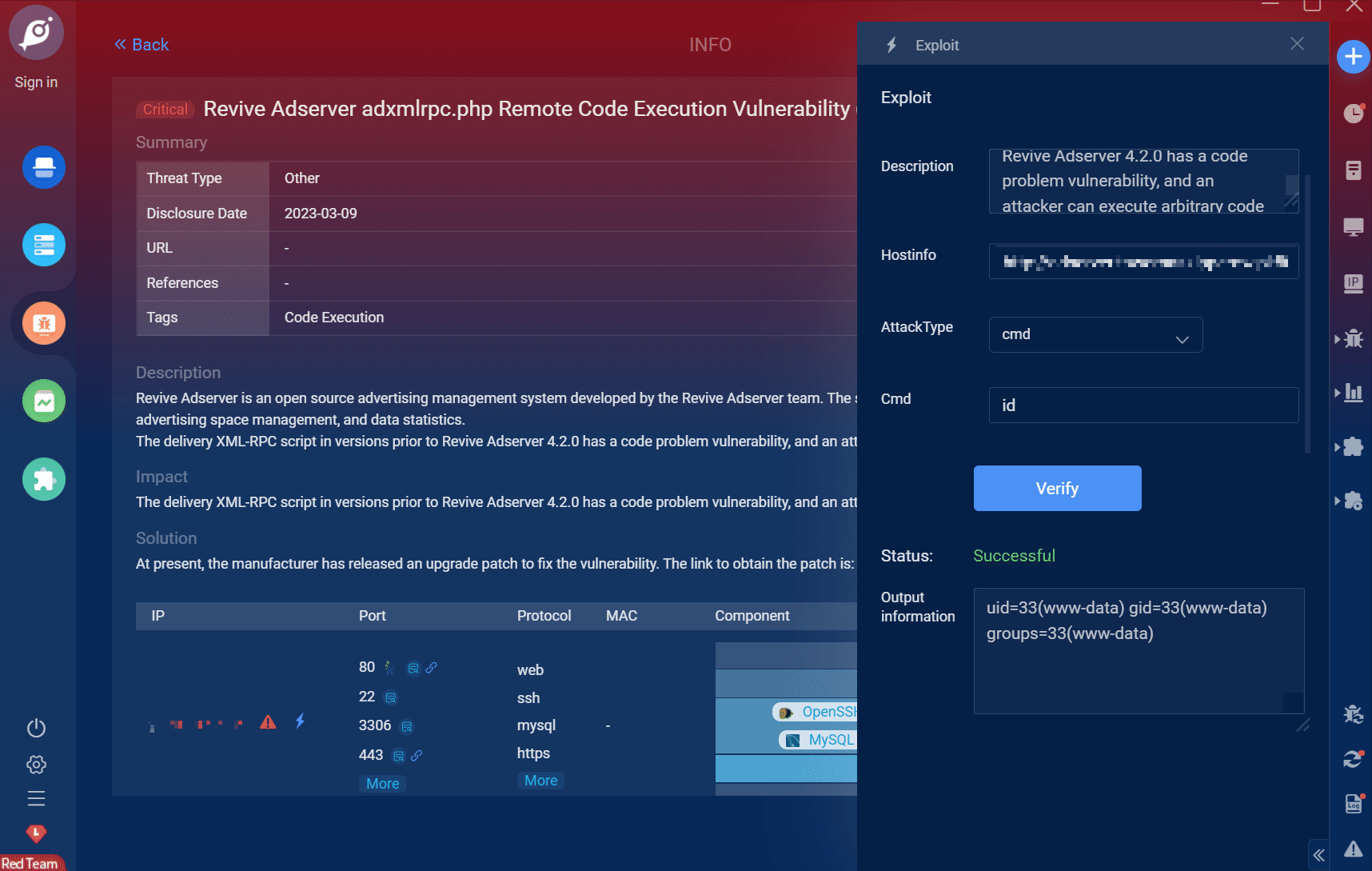
Goby 漏洞发布|Revive Adserver 广告管理系统 adxmlrpc.php 文件远程代码执行漏洞(CVE-2019-5434)
漏洞名称:Revive Adserver 广告管理系统 adxmlrpc.php 文件远程代码执行漏洞(CVE-2019-5434) English Name: Revive Adserver adxmlrpc.php Remote Code Execution Vulnerability (CVE-2019-5434) CVSS core: 9.0 影响资产数&a…...
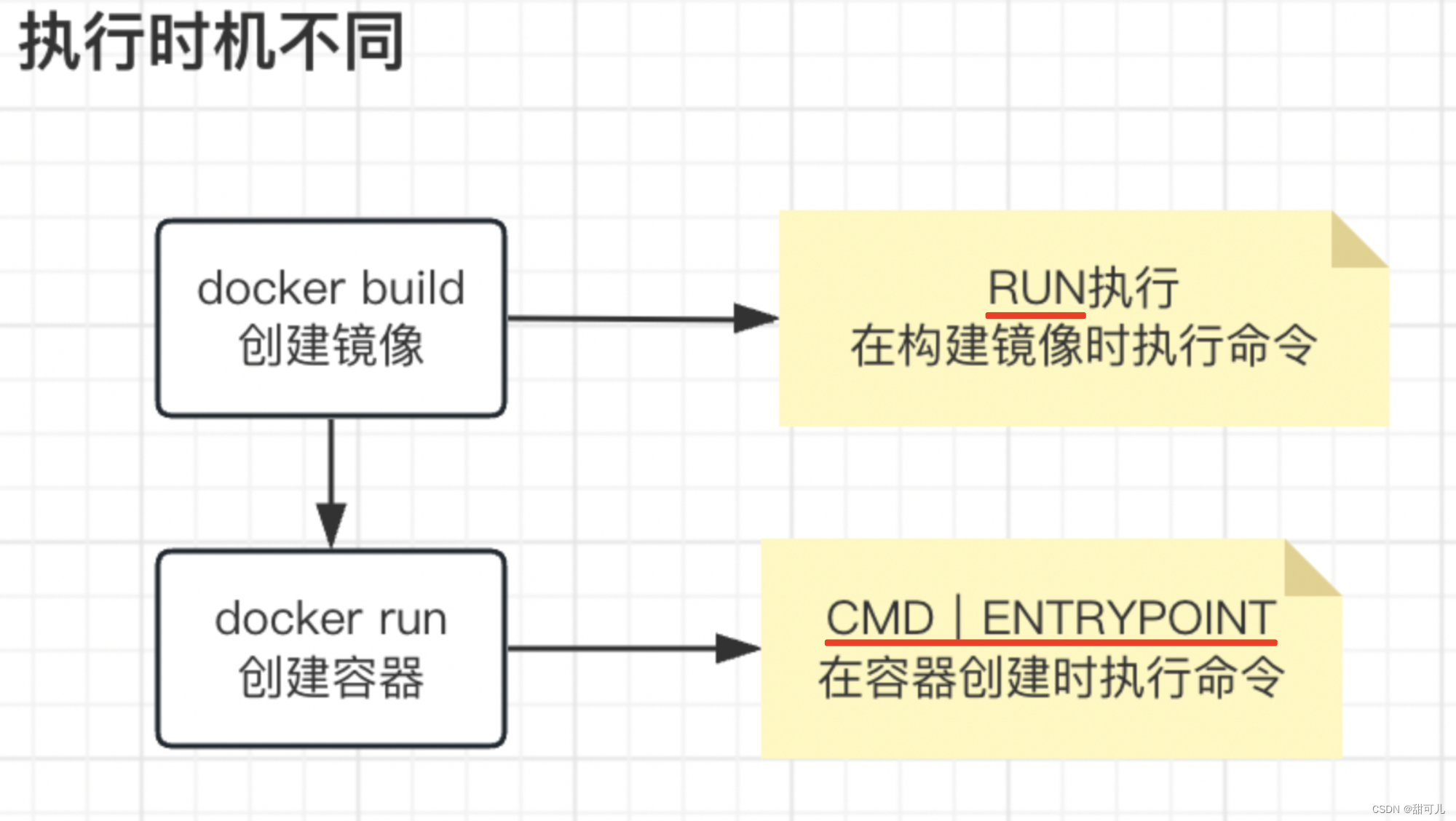
Docker(三)、Dockerfile探究
Dockerfile探究 一、镜像层概念1、通过执行命令显化docker的机制 二、Dockerfile基础命令1、FROM 基于基准镜像【即构建镜像的时候,依托原有镜像做拓展】2、LABEL & MAINTAINER -说明信息3、WORKDIR 设置工作目录4、ADD & COPY 复制文件5、ENV 设置环境常量…...

C++读取文件夹下多个文件,包括图片等等
话不多说,直接上代码: int main() {//读入图片路径下的所有文件,D:\APP\VS\vs_projects_repos\Isp\imagesstring imgdirpath"D:\\APP\\VS\\vs_projects_repos\\Isp\\proimages\\";// 只读取文件夹下的png的文件名,也可以改成“*.b…...
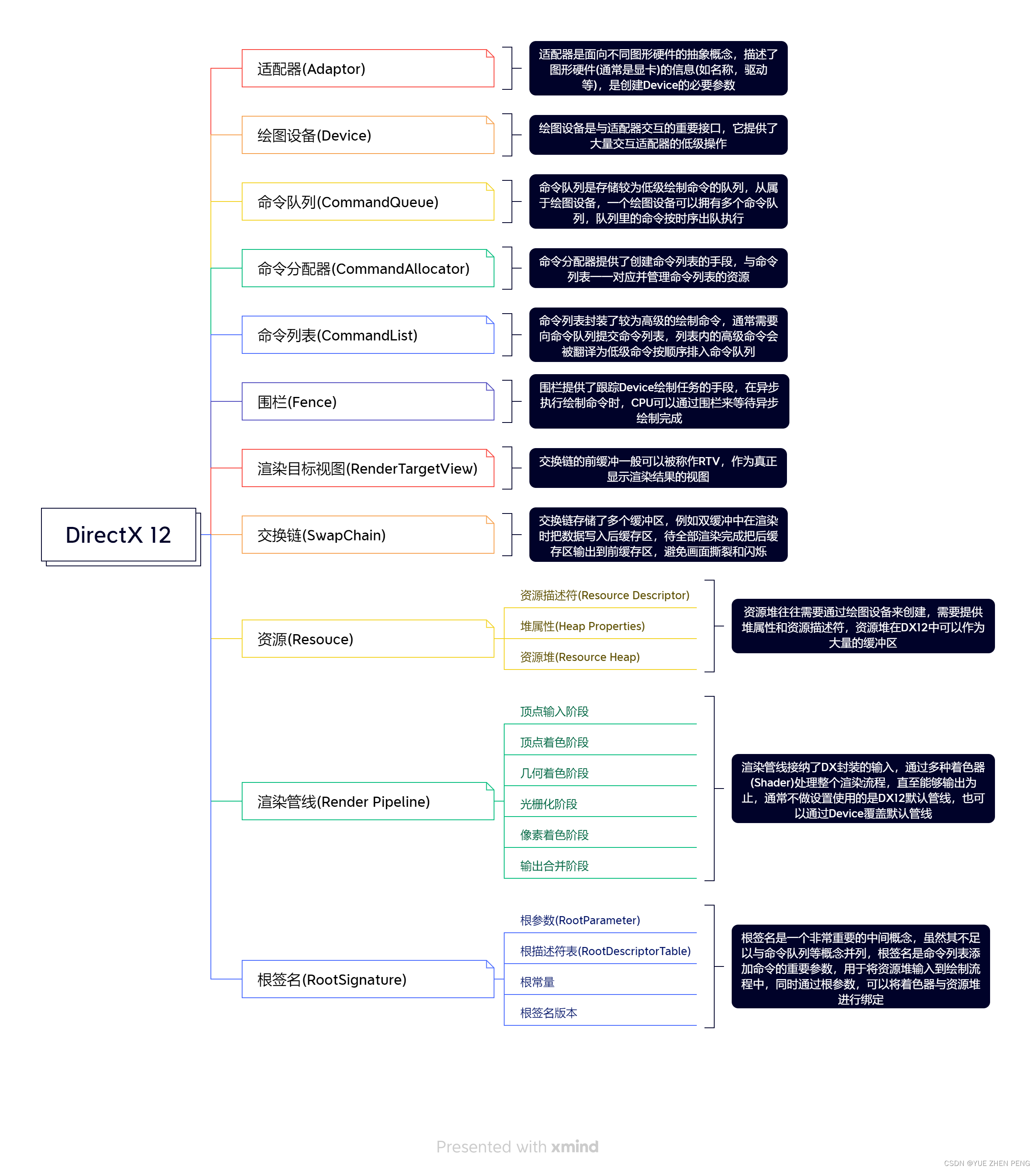
DirectX 12 学习笔记 -结构
上篇文章我们创建了一个窗口,看样子还不难,我们继续玩DX12 引用一些文件 头文件 #include <d3d12.h> #include <dxgi1_4.h> #include <wrl.h>还有一些库 #pragma comment(lib, "d3d12.lib") #pragma comment(lib, "…...
之在 Redis使用 lua 脚本)
【Redis】Redis 的学习教程(十二)之在 Redis使用 lua 脚本
lua 菜鸟教程:https://www.runoob.com/lua/lua-tutorial.html 在 Redis 使用 lua 脚本的好处: 减少网络开销。可以将多个请求通过脚本的形式一次发送,减少网络时延及开销原子性操作。Redis会将整个脚本作为一个整体执行,中间不会…...

标准/扩展库中对象的导入与使用
博主:命运之光 专栏:Python程序设计 Python扩展库导入和使用 Python启动时,仅加载了很少一部分模块,其它模块需要由程序员显示加载。使用“sys.modules.items()”显示所有预加载的模块信息。 import 模块名[.对象名] [as 别名] …...

87、Redis 的 value 所支持的数据类型(String、List、Set、Zset、Hash)---->List相关命令
本次讲解要点: List相关命令:是指value中的数据类型 启动redis服务器: 打开小黑窗: C:\Users\JH>e: E:>cd E:\install\Redis6.0\Redis-x64-6.0.14\bin E:\install\Redis6.0\Redis-x64-6.0.14\bin>redis-server.exe redi…...

Celery结合flask完成异步任务与定时任务
Celery 常用于 web 异步任务、定时任务等。 使用 redis 作为 Celery的「消息代理 / 消息中间件」。 这里通过Flask-Mail使用qq邮箱延时发送邮件作为示例 pip install celery pip install redis pip install Flask-Mail1、使用flask发送邮件 使用 Flask-Mail 发送邮件需要进行…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
