Python集成开发环境（IDE）：WingPro for Mac
WingPro for Mac是一款Python集成开发环境（IDE）软件，它提供了一系列强大的工具和功能，帮助Python开发人员提高开发效率和质量。
WingPro for Mac拥有直观的用户界面和强大的调试器，可以帮助用户快速定位问题和修复错误。它还提供了智能代码补全、语法高亮、代码折叠等功能，使编写Python代码更加方便和快速。此外，WingPro for Mac还支持各种Python框架和库，包括Django、Flask、Pyramid等，使得开发人员可以更加轻松地编写Python应用程序。
总的来说，WingPro for Mac是一款非常实用的Python开发工具，为开发人员提供了强大的功能和工具，帮助他们更加高效地编写Python代码。
WingPro mac版破解教程
软件下载完成后，先双击python.pkg根据提示进行安装
将左侧的WingPro拖到右侧的应用程序进行安装
运行wingpro ，点击accept,选择Activate a purchased license，先放一边待用。
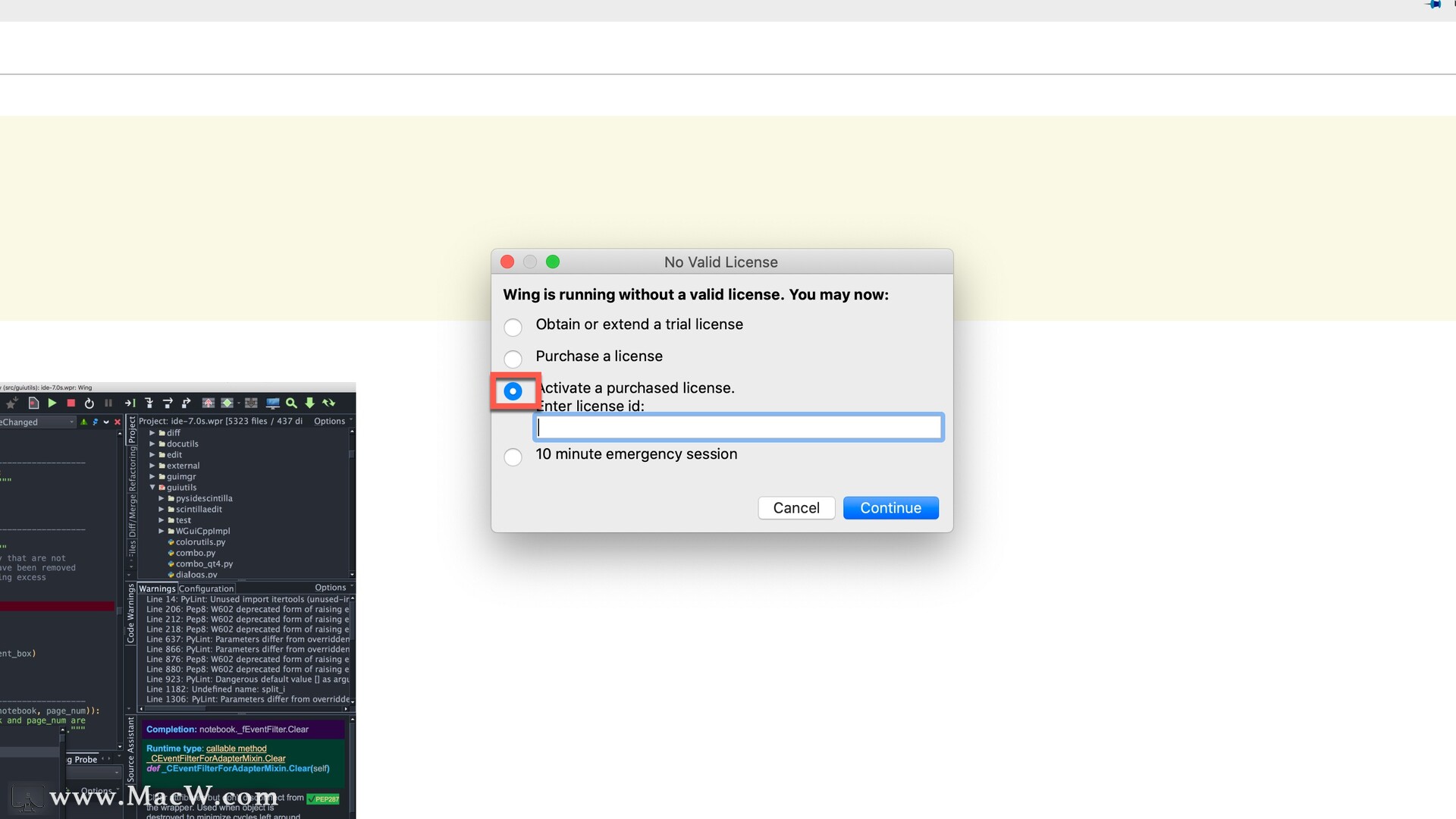
将镜像包中的wingpro破解工具keygen9.pyc拖到桌面
打开终端，输入python3注意python3后面需加一个空格
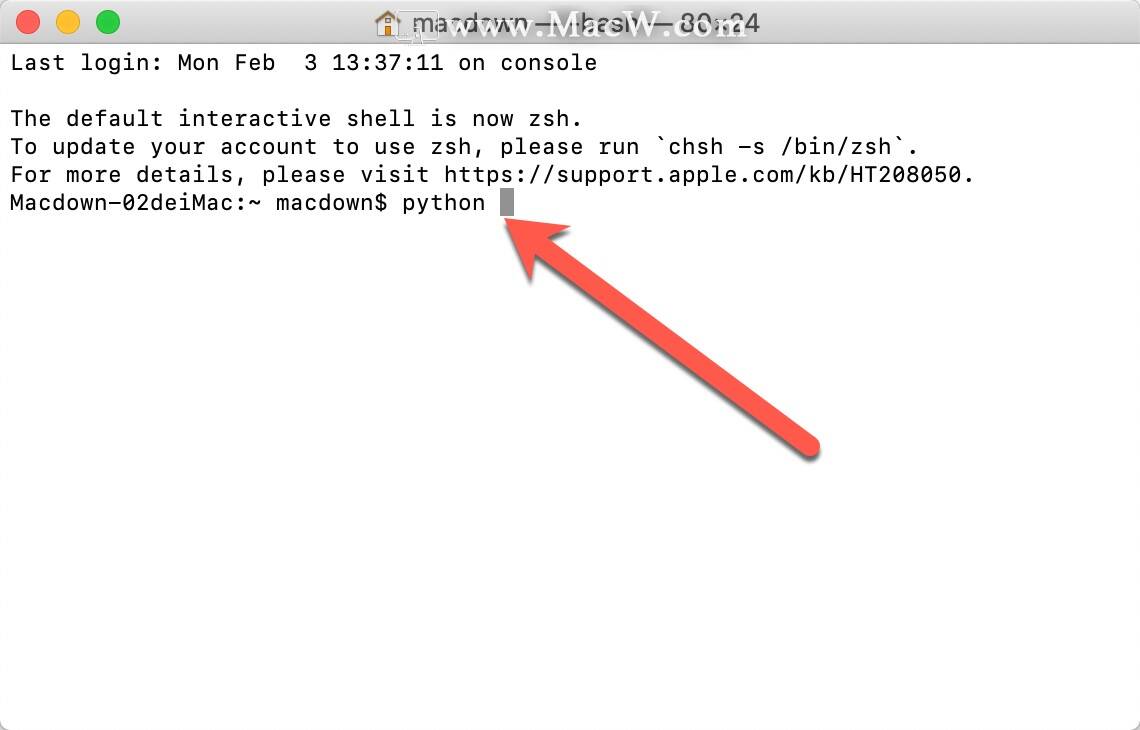
把wingpro破解工具拖进终端并回车
提示输入密码，输入avh.world后回车
此时终端会生成一串wingpro注册码。
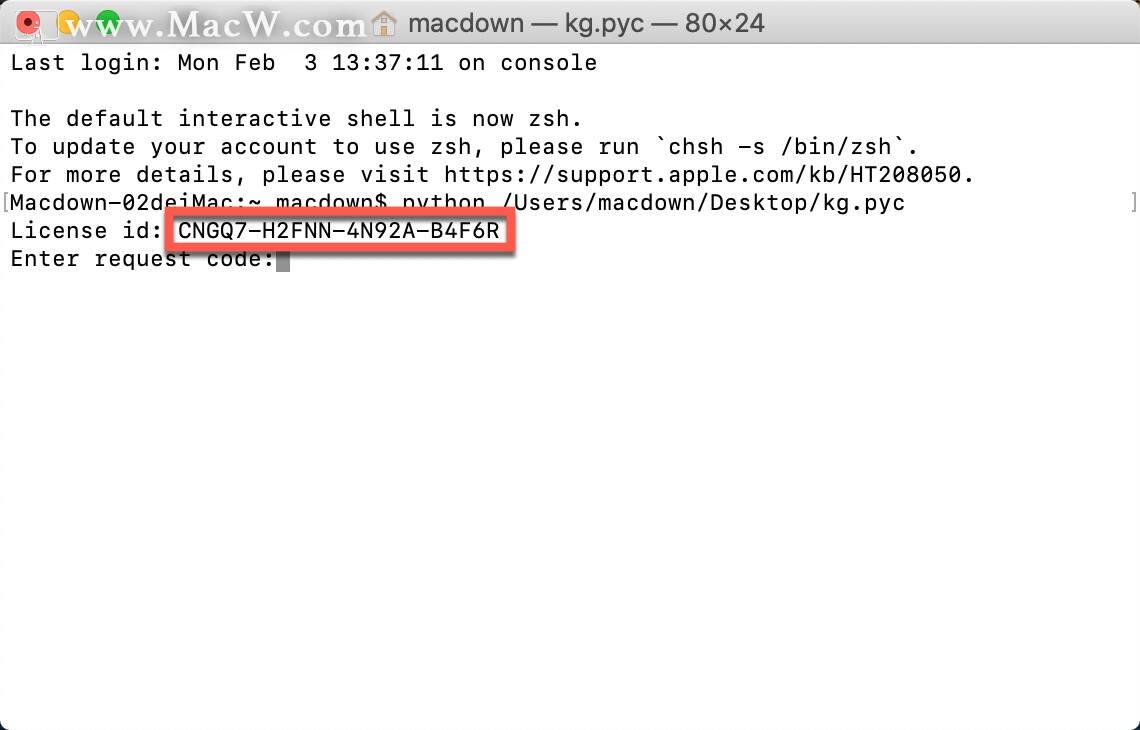
把wingpro注册码复制到软件注册页面。如若不行，重新启动终端重试！ wingpro注册码输入之后请点击continue
把wingpro软件中生成的request code复制到终端中，然后点击回车。
终端会生成另一串WingIDE注册密钥，把WingIDE密钥复制到软件注册页面的正确位置中，再点击Continue
wingpro mac 破解版提示您注册成功！！
相关文章：
Python集成开发环境（IDE）：WingPro for Mac
WingPro for Mac是一款Python集成开发环境（IDE）软件，它提供了一系列强大的工具和功能，帮助Python开发人员提高开发效率和质量。 WingPro for Mac拥有直观的用户界面和强大的调试器，可以帮助用户快速定位问题和修复错误…...
[Machine learning][Part3] numpy 矢量矩阵操作的基础知识
很久不接触数学了，machine learning需要用到一些数学知识，这里在重温一下相关的数学基础知识 矢量 矢量是有序的数字数组。在表示法中，矢量用小写粗体字母表示。矢量的元素都是相同的类型。例如，矢量不包含字符和数字。数组中元…...
【中秋国庆不断更】HarmonyOS对通知类消息的管理与发布通知（上）
一、通知概述 通知简介 应用可以通过通知接口发送通知消息，终端用户可以通过通知栏查看通知内容，也可以点击通知来打开应用。 通知常见的使用场景： 显示接收到的短消息、即时消息等。显示应用的推送消息，如广告、版本更新等。显示…...
喜讯 | 怿星科技获评SAE“优秀核心零部件企业”，测试软件平台工具广受赞誉
2023年9月22日-23日，SAE 2023汽车智能与网联技术国际学术会议成功举行。此次学术会议由SAE International与南昌智能新能源汽车研究院联合主办，大会汇聚了来自国内外智能网联领域的顶尖专家和学者。大会同期颁布的奖项旨在向行业推选出更多新时代涌现的杰…...
基于Java的医院预约挂号系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序（小蔡coding）有保障的售后福利 代码参考源码获取 前言 💗博主介绍：✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...
福利！这两款我自制的免费配色工具你领到了吗？
前两天刚入职，还没干过啥活儿，就迎来了中秋3天国庆7天总共8天的假期，美滋滋。 在这么喜庆的日子里，我觉得大家应该也无心科研，所以不如给大家发点儿福利，继续乐呵乐呵。 当然，说是福利&…...
Docker 网桥、docker0 网桥和 --net host：平台差异、使用方式和场景介绍简介：
Docker 是一个流行的容器化平台，它提供了不同的网络配置选项。其中，Docker 网桥、docker0 网桥和 --net host 是常见的网络部署方式。本文将介绍这些网络选项的平台差异、使用方式以及适用的场景。 Docker 网桥 (Bridge Networking)：Docker 网桥是 Docker 默认的网络模式。在…...
【深度学习】系统架构工具链的学习笔记
1. 数据管理 数据版本控制和数据包管理：Activeloop Note: Scale Nucleus：其GitHub（nucleus-python-client）的stars数量少于 Deep Lake。Quilt：其GitHub（quilt）的stars数量少于 Deep Lake。...
Linux 网络编程
套接字（Socket）： 通过网络实现跨机通信 作用：一种文件描述符传输层的文件描述符 整个编程中，需要着重注意htonl/htons、ntohl/ntohs、inet_addr等 TCP的C/S实现 循环服务器模型 TCP服务器实现过程 1.创建套接字&a…...
SpringBoot读取配置的方式
在 Spring Boot 应用中，我们通常需要一些配置信息来指导应用的运行。这些配置信息可以包括如下内容：端口号、数据库连接信息、日志配置、缓存配置、认证配置、等等。Spring Boot 提供了多种方式来读取这些配置信息。读取配置的目的是为了在程序中使用这些…...
c# winform程序，DispatcherTimer被调用延迟，响应间隔长
c# winform程序，DispatcherTimer被调用延迟，响应间隔长 最近修改的问题，winform界面上两个控件的数据刷新，用DispatcherTimer定时刷新，但是在某些机器上的实际刷新时间间隔远远大于设置时间。 既然MSDN已经说了&…...
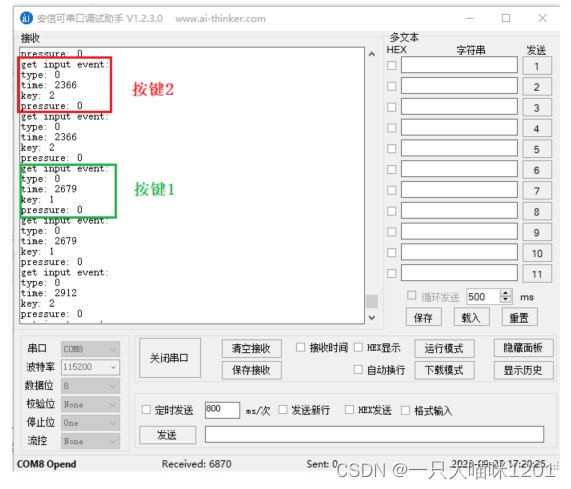
【智能家居项目】裸机版本——项目介绍 | 输入子系统(按键) | 单元测试
🐱作者：一只大喵咪1201 🐱专栏：《智能家居项目》 🔥格言：你只管努力，剩下的交给时间！ 目录 🏀项目简介🏀输入子系统(按键)⚽应用层⚽设备层⚽ 内核层抽象层⚽…...
算法练习8——有序三元组中的最大值
LeetCode 100088 有序三元组中的最大值 I LeetCode 100086 有序三元组中的最大值 II 给你一个下标从 0 开始的整数数组 nums 。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中，找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数&am…...
git创建
问: git remote add origin https://github.com//blog.git fatal: not a git repository (or any of the parent directories): .git 回答: 这个错误提示指出当前目录或其父目录中不存在.git文件夹，因此无法执行git相关操作。请确保你是在一个已经初始化为git仓库…...
yolov8 opencv模型部署（python版）
yolov8 opencv模型部署（python版） 使用opencv推理yolov8模型，以yolov8n为例子，一共几十行代码，没有废话，给出了注释，从今天起，少写一行代码，少掉一根头发。测试数据有需…...
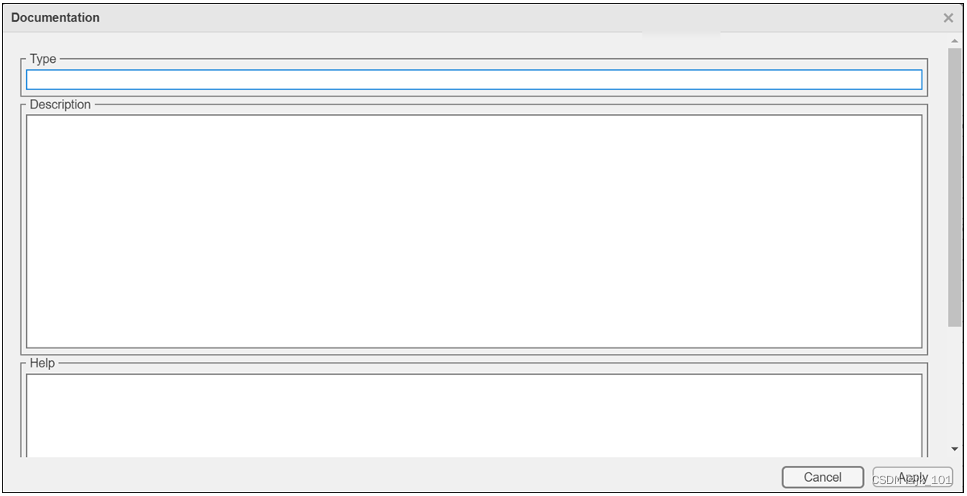
Simulink仿真封装中的参数个对话框设置
目录 参数和对话框窗格 初始化窗格 文档窗格 为了更加直观和清晰的分析仿真，会将多个元件实现的一个功能封装在一起，通过参数对话框窗格，可以使用参数、显示和动作选项板中的对话框控制设计封装对话框。如图所示： 参数和对话框…...
【C++】class的设计与使用（十）重载iostream运算符
希望对某个类对象进行读写操作，直接cout<<类对象<<endl;或cin>>类对象;编译器会报错，所以我们必须提供一份重载的input/output运算符： 重载ostream运算符 ostream& operator<<(ostream &os, const Triangu…...
Java使用Scanner类实现用户输入与交互
概述： Scanner类是Java中的一个重要工具类，用于读取用户的输入。它提供了一系列的方法，可以方便地读取不同类型的数据，如整数、浮点数、字符串等。在本文中，我们将详细介绍Scanner类的使用方法，并通过两个…...
FFmpeg 命令：从入门到精通 | ffppeg 命令参数说明
FFmpeg 命令：从入门到精通 | ffmpeg 命令参数说明 FFmpeg 命令：从入门到精通 | ffmpeg 命令参数说明主要参数音频参数视频参数更多参考 FFmpeg 命令：从入门到精通 | ffmpeg 命令参数说明 本节主要介绍了 ffmpeg 命令的常用参数。 主要参数 …...
Chrome(谷歌浏览器)如何关闭搜索栏历史记录
目录 问题描述解决方法插件解决（亲测有效）自带设置解决步骤首先打开 地址 输入：chrome://flags关闭浏览器，重新打开Chrome 发现 已经正常 问题描述 Chrome是大家熟知的浏览器，但是搜索栏的历史记录如何自己一条条的删…...
SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题（可多选） 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘：专注于发现数据中…...
Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面（Target 选项卡）1. IROM1（用于配置 Flash）2. IRAM1（用于配置 RAM）二、链接器设置界面（Linker 选项卡）1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数（如果没有勾选上面…...
第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代，智能代理（agents）不再是孤立的个体，而是能够像一个数字团队一样协作。然而，当前 AI 生态系统的碎片化阻碍了这一愿景的实现，导致了“AI 巴别塔问题”——不同代理之间…...
解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上，所以报错，到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本，cu、torch、cp 的版本一定要对…...
工业自动化时代的精准装配革新：迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年，作为行业领先的3D工业相机及视觉系统供应商，累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成，通过稳定、易用、高回报的AI3D视觉系统，为汽车、新能源、金属制造等行…...
深入解析C++中的extern关键字：跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析：跨文件编程的终极指南 📅 更新时间：2025年6月5日 🏷️ 标签：C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么？&…...
算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer （1）资源 论文&a…...
PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
系统掌握PyTorch：图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长，建议点赞收藏，以免遗失。更多AI大模型应用开发学习视频及资料，尽在聚客AI学院。 本文通过代码驱动的方式，系统讲解PyTorch核心概念和实战技巧，涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
论文阅读：Matting by Generation
今天介绍一篇关于 matting 抠图的文章，抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法，已经有很多的工作和这个任务相关。这两年 diffusion 模型很火，大家又开始用 diffusion 模型做各种 CV 任务了&am…...