怒刷LeetCode的第16天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:迭代
方法二:模拟
方法三:循环模拟
方法四:传递
第二题
题目来源
题目内容
解决方法
方法一:回溯
方法二:枚举优化
第三题
题目来源
题目内容
解决方法
方法一:递归
方法二:迭代
方法三:动态规划
方法四:递推
第一题
题目来源
2582. 递枕头 - 力扣(LeetCode)
题目内容

解决方法
方法一:迭代
这个问题可以使用一个简单的循环来解决。我们使用两个变量来追踪当前拿着枕头的人的位置和传递的方向。
- 首先,我们初始化forward为true,表示初始传递方向是向前的。然后,我们进入一个循环,从1到time进行迭代,模拟枕头传递的过程。
- 在循环中,我们首先检查当前拿着枕头的人是否处于队列的首位(即pos == 1),如果是,则将传递方向设置为向前(forward = true);然后,我们检查当前拿着枕头的人是否处于队列的末尾(即pos == n),如果是,则将传递方向设置为向后(forward = false)。
- 接下来,我们根据传递方向更新当前拿着枕头的人的位置。如果传递方向是向前(forward = true),则将pos加1;如果传递方向是向后(forward = false),则将pos减1。
- 重复这个过程,直到达到指定的传递时间time。最后,返回拿着枕头的人的编号pos。
总结来说,我们使用一个循环来迭代传递过程,并根据当前位置和传递方向进行更新,直到达到指定的传递时间。最终,返回拿着枕头的人的编号。
class Solution {public int passThePillow(int n, int time) {boolean forward = true;int pos = 1;for (int i = 1; i <= time; i++) {if (pos == 1) {forward = true;} else if (pos == n) {forward = false;}if (forward) {pos++;} else {pos--;}}return pos;}
}
复杂度分析:
- 时间复杂度分析:循环的次数取决于传递的时间time,因此循环的次数是常数级别的。所以,时间复杂度可以表示为O(1),即常数时间复杂度。
- 空间复杂度分析:在这个算法中,并没有使用任何额外的数据结构,只使用了几个整型变量来追踪位置和方向。因此,空间复杂度是O(1),即常数空间复杂度。
综上所述,该算法具有常数级别的时间复杂度和空间复杂度。这意味着无论输入的传递时间time和参与传递的人数n有多大,算法的执行时间和空间占用都是固定的。
LeetCode运行结果:
方法二:模拟
这个算法的思路是通过观察规律,找到一个公式计算出时间t后枕头所在位置的编号。
首先,我们可以注意到,每当枕头到达队伍的某一端,就会改变传递方向。也就是说,枕头的传递方向是周期性的,以(n-1)*2为一个周期。例如,当n=4时,第一次周期内,枕头的传递顺序是1-2-3-4-3-2;第二次周期内,枕头的传递顺序是2-3-4-3-2-1。因此,我们可以将time对于一个周期取模,以便更好地处理时间过长的情况。
接下来,考虑如何计算枕头所在位置的编号。如果time小于n,此时枕头仍然在最开始的n个人中间传递,因此枕头的位置等于time+1。否则,枕头已到达了队伍的另一端,需要反向传递。如果按顺序数枕头位置,此时与time相对应的枕头位置应该是n*2-time-1,因此可以使用这个表达式计算枕头所在的位置编号。
class Solution {public int passThePillow(int n, int time) {time %= (n - 1) * 2;return time < n ? time + 1 : n * 2 - time - 1;}
}
复杂度分析:
- 时间复杂度分析:在这个算法中,我们只有一个简单的求模运算和一个条件判断,所以时间复杂度为O(1),即常数时间复杂度。
- 空间复杂度分析:该算法没有使用任何额外的数据结构或递归调用,所以空间复杂度为O(1),即常数空间复杂度。不论输入的大小,所需的额外空间都是固定的。
综上所述,该算法的时间复杂度为O(1),空间复杂度为O(1)。
LeetCode运行结果:
方法三:循环模拟
这个算法的思路是使用一个循环来模拟枕头传递过程,每次选择下一个接收枕头的人的位置。
- 首先,我们初始化两个变量ans和k,分别表示当前枕头所在的位置和传递的方向。初始时,枕头在位置1,传递方向为向右。
- 然后,我们进入一个循环,循环执行time次。在每一次循环中,首先将ans的值增加k,以选取下一个接收枕头的位置(如果k为1,则向右移动一位;如果k为-1,则向左移动一位)。然后,如果ans等于1或者等于n,表示枕头到达队伍的一端,需要改变传递方向,即将k乘以-1。
- 重复上述步骤,直到循环执行完time次,最后返回ans即为最终枕头所在的位置编号。
class Solution {public int passThePillow(int n, int time) {int ans = 1, k = 1;while (time-- > 0) {ans += k;if (ans == 1 || ans == n) {k *= -1;}}return ans;}
}
复杂度分析:
- 时间复杂度分析:在这个算法中,循环执行time次,因此时间复杂度为O(time)。虽然time是一个变量,但是在实际应用中,time一般是一个较小的固定值。
- 空间复杂度分析:该算法只使用了几个整型变量,不随输入规模变化,因此空间复杂度为O(1),即常数空间复杂度。
综上所述,该算法的时间复杂度为O(time),空间复杂度为O(1)。
LeetCode运行结果:
方法四:传递
这个算法的思路是,先计算出枕头到达队伍的另一端需要经过几次传递,然后根据剩余传递次数和当前位置计算最终位置。
- 首先,我们可以注意到,在N个人的队伍中,每当枕头到达队伍的某一端,就会经过N-1个人的传递。也就是说,每N-1个传递为一个周期,枕头在经过一个周期后,就会回到原来的位置并改变传递方向。因此,我们可以先计算出枕头要经过几个周期才能到达队伍的另一端。
- 接着,我们将time除以n-1得到k,表示枕头需要经过k个周期。然后,对n-1取模得到mod,表示枕头在进行完k个周期后还要经过mod次传递。
- 最后,我们根据当前位置和剩余传递次数计算最终位置。如果经过k个周期后,枕头处于队伍的左侧(即k为偶数),则最终位置为当前位置加上mod;否则,最终位置为n-mod(反向传递)。
class Solution {public int passThePillow(int n, int time) {int k = time / (n - 1);int mod = time % (n - 1);return (k & 1) == 1 ? n - mod : mod + 1;}
}
复杂度分析:
- 时间复杂度分析:在这个算法中,我们只进行了几次简单的整数运算,因此时间复杂度为O(1),即常数时间复杂度。
- 空间复杂度分析:该算法只使用了几个整型变量,不随输入规模变化,因此空间复杂度为O(1),即常数空间复杂度。
综上所述,该算法的时间复杂度为O(1),空间复杂度为O(1)。
LeetCode运行结果:
第二题
题目来源
37. 解数独 - 力扣(LeetCode)
题目内容


解决方法
方法一:回溯
这道题可以通过回溯算法来解决。回溯算法是一种暴力搜索的算法,它尝试在数独的空格中填入数字,并检查填入是否满足数独的规则。如果满足,则继续下一个空格;如果不满足,则回退到上一个空格重新选择数字。
具体实现时,可以使用递归函数来进行回溯。递归函数的参数可以包括数独数组、当前要填入的行和列。在每个空格中,我们尝试填入数字 1-9,并检查是否满足数独的规则。如果满足,则递归调用下一个空格;如果不满足,则尝试下一个数字。直到填完所有的空格,或者找到了一个有效的解为止。
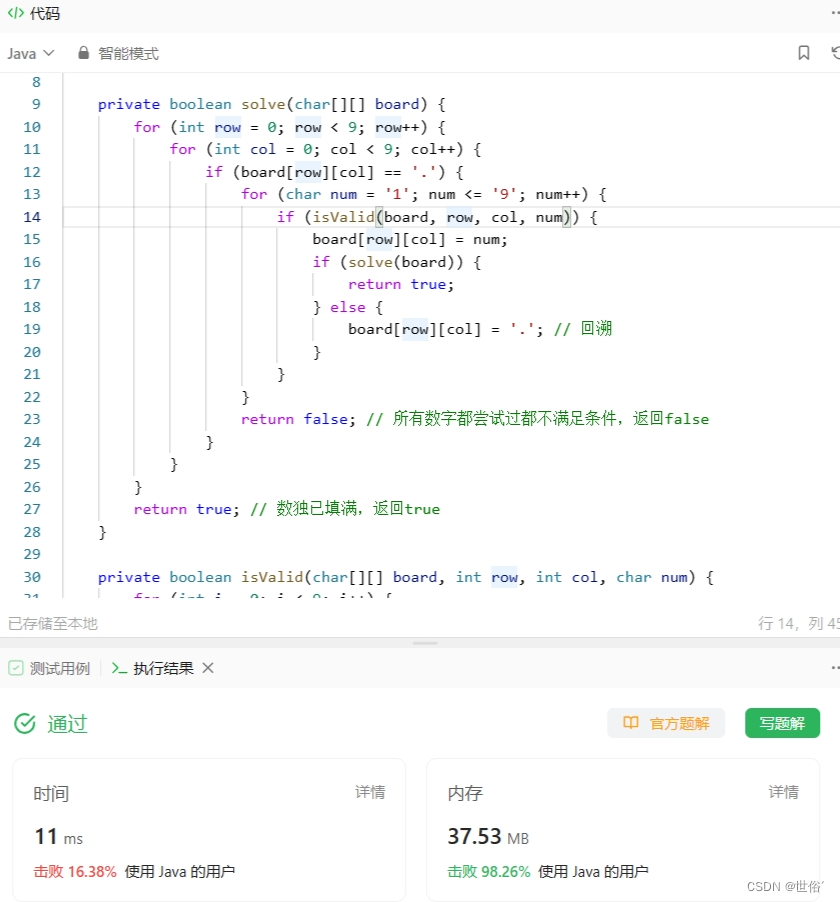
class Solution {public void solveSudoku(char[][] board) {if (board == null || board.length == 0) {return;}solve(board);}private boolean solve(char[][] board) {for (int row = 0; row < 9; row++) {for (int col = 0; col < 9; col++) {if (board[row][col] == '.') {for (char num = '1'; num <= '9'; num++) {if (isValid(board, row, col, num)) {board[row][col] = num;if (solve(board)) {return true;} else {board[row][col] = '.'; // 回溯}}}return false; // 所有数字都尝试过都不满足条件,返回false}}}return true; // 数独已填满,返回true}private boolean isValid(char[][] board, int row, int col, char num) {for (int i = 0; i < 9; i++) {if (board[i][col] == num) { // 检查列是否重复return false;}if (board[row][i] == num) { // 检查行是否重复return false;}int subBoxRow = 3 * (row / 3) + i / 3; // 检查小宫格是否重复int subBoxCol = 3 * (col / 3) + i % 3;if (board[subBoxRow][subBoxCol] == num) {return false;}}return true;}
}
复杂度分析:
时间复杂度:
- 遍历数独空格:O(81),因为数独是固定的9x9大小,所以遍历所有的空格需要O(81)的时间复杂度。
- 递归尝试填入数字:在每个空格中,我们尝试填入1-9的数字,所以对于每个空格,尝试的次数为常数,所以总的尝试次数为O(1)。
- 判断填入的数字是否满足数独规则:在判断一个数字在行、列、3x3宫格中是否重复时,我们需要遍历相关的行、列和宫格,每次都是常数时间操作,所以总的判断时间为O(1)。 综上所述,整个数独解法的时间复杂度为O(81 * 1 * 1) = O(81)。
空间复杂度:
- 递归栈空间:递归函数的调用会使用一定的栈空间,递归的最大深度不会超过空格的数量,所以空间复杂度为O(m),其中m是空格的数量。对于数独问题来说,空格的数量最多为81个,所以空间复杂度为O(81) = O(1)。
- 数独数组修改:原地修改数独数组,不需要使用额外空间,所以空间复杂度为O(1)。
综上所述,数独解法的总体空间复杂度为O(1),时间复杂度为O(81)。
LeetCode运行结果:
方法二:枚举优化
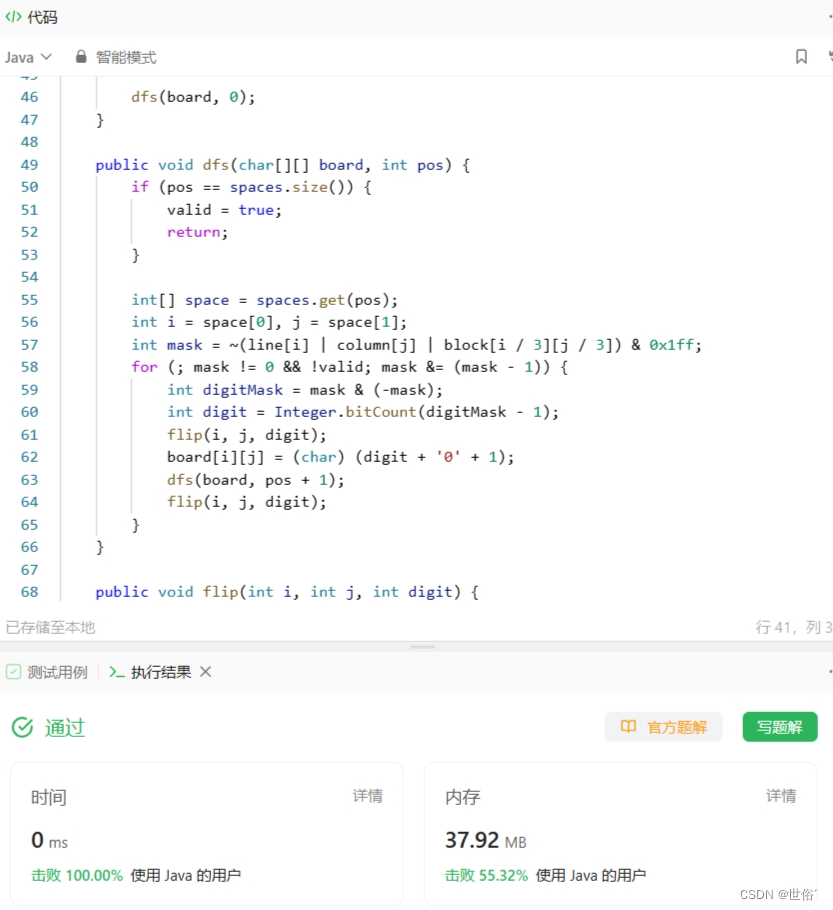
class Solution {private int[] line = new int[9];private int[] column = new int[9];private int[][] block = new int[3][3];private boolean valid = false;private List<int[]> spaces = new ArrayList<int[]>();public void solveSudoku(char[][] board) {for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] != '.') {int digit = board[i][j] - '0' - 1;flip(i, j, digit);}}}while (true) {boolean modified = false;for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] == '.') {int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;if ((mask & (mask - 1)) == 0) {int digit = Integer.bitCount(mask - 1);flip(i, j, digit);board[i][j] = (char) (digit + '0' + 1);modified = true;}}}}if (!modified) {break;}}for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] == '.') {spaces.add(new int[]{i, j});}}}dfs(board, 0);}public void dfs(char[][] board, int pos) {if (pos == spaces.size()) {valid = true;return;}int[] space = spaces.get(pos);int i = space[0], j = space[1];int mask = ~(line[i] | column[j] | block[i / 3][j / 3]) & 0x1ff;for (; mask != 0 && !valid; mask &= (mask - 1)) {int digitMask = mask & (-mask);int digit = Integer.bitCount(digitMask - 1);flip(i, j, digit);board[i][j] = (char) (digit + '0' + 1);dfs(board, pos + 1);flip(i, j, digit);}}public void flip(int i, int j, int digit) {line[i] ^= (1 << digit);column[j] ^= (1 << digit);block[i / 3][j / 3] ^= (1 << digit);}
}这段代码使用了位运算和深度优先搜索来解决数独问题。下面是算法的思路:
- 初始化
line、column和block数组,用于记录每行、每列和每个九宫格中已经出现的数字状态。 - 遍历整个数独棋盘,对于已填入数字的格子,更新相应的状态数组。
- 使用循环,不断尝试填入数字,直到无法再填入为止。在每次循环中,遍历棋盘上的每个空白格子,并计算可填入数字的条件:
- 通过位运算计算出当前格子可用的数字(即未出现在同一行、同一列和同一个九宫格中的数字)。
- 如果仅有一个数字满足条件,则将其填入,并更新状态数组。
- 如果有多个数字满足条件,则跳过该格子,继续下一个格子。
- 遍历完成后,如果仍存在空白格子,将它们的位置保存在
spaces列表中。 - 调用深度优先搜索函数
dfs,递归地尝试填入空白格子:- 如果已经填完所有空白格子,设定
valid为真并返回。 - 取出下一个空白格子的位置,计算可填入的数字的条件。
- 通过位运算,逐个尝试可填入的数字,并进行递归搜索。
- 如果已经填完所有空白格子,设定
- 如果搜索到最后,仍未找到合法解,则将之前填入的数字恢复,并返回上一层继续搜索其他可能的数字组合。
这种解法通过位运算和状态压缩技巧,提高了数独求解的效率。同时使用深度优先搜索来穷举所有可能的数字组合,直到找到合法解或遍历完所有空白格子。
复杂度分析:
时间复杂度:
- 初始化部分需要遍历数独棋盘,时间复杂度为O(81) = O(1)。
- 循环填入数字的部分,最坏情况下需要进行多轮循环,但每轮循环中每个格子的操作是常数时间的,因此可以认为整体时间复杂度为O(81) = O(1)。
- 深度优先搜索部分,最坏情况下需要穷举所有可能的数字组合,并且每个格子都有9种选择,因此时间复杂度为O(9^(空白数量))。空白数量通常较小,因此可以近似看作常数,即O(1)。 综上所述,整体时间复杂度为O(1)。
空间复杂度:
- 使用了line、column和block数组来记录数字出现的状态,每个数组的长度为9,因此空间复杂度为O(9) = O(1)。
- 使用了spaces列表来保存空白格子的位置,最多有81个空白格子,因此空间复杂度为O(81) = O(1)。
- 递归调用dfs函数时产生的函数调用栈空间,最多深度为空白数量,通常较小,因此空间复杂度为O(1)。 综上所述,整体空间复杂度为O(1)。
总结起来,该算法的时间复杂度和空间复杂度都是O(1),表示算法的运行时间和占用的额外空间都与输入规模无关,非常高效。
LeetCode运行结果:
第三题
题目来源
38. 外观数列 - 力扣(LeetCode)
题目内容


解决方法
方法一:递归
要解决这个问题,我们可以使用递归的方法来生成外观数列。首先,定义一个递归函数generateNext,该函数输入一个数字字符串,并返回对其进行描述后的新字符串。然后,我们可以使用递归调用generateNext来生成外观数列的第n项。
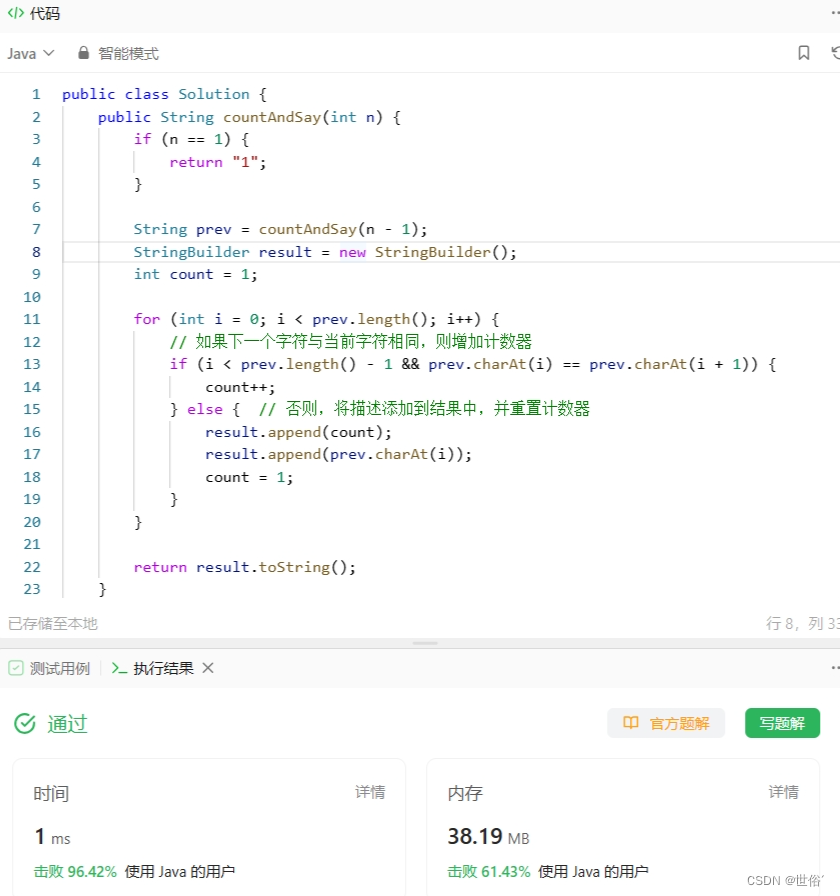
public class Solution {public String countAndSay(int n) {if (n == 1) {return "1";}String prev = countAndSay(n - 1);StringBuilder result = new StringBuilder();int count = 1;for (int i = 0; i < prev.length(); i++) {// 如果下一个字符与当前字符相同,则增加计数器if (i < prev.length() - 1 && prev.charAt(i) == prev.charAt(i + 1)) {count++;} else { // 否则,将描述添加到结果中,并重置计数器result.append(count);result.append(prev.charAt(i));count = 1;}}return result.toString();}
}
在上面的代码中,当n为1时,直接返回"1";否则,先递归调用countAndSay(n - 1)来得到前一项的描述字符串,然后遍历该字符串,统计相邻相同字符的个数,并将个数和字符添加到结果中。最后,返回结果字符串。通过调用countAndSay函数,可以得到外观数列的第n项。
复杂度分析:
- 时间复杂度分析:
- 对于每一项n,我们需要递归调用`countAndSay(n - 1)`来得到前一项的描述字符串。因此,总共需要进行n次递归调用。
- 在每一次递归调用中,我们需要遍历前一项的描述字符串,计算相邻相同字符的个数,并将结果添加到结果中。这一步的时间复杂度是O(len(prev)),其中len(prev)表示前一项描述字符串的长度。
- 综上所述,总的时间复杂度是O(1 + 2 + 3 + ... + n) = O(n^2),其中n是给定的正整数。
空间复杂度分析:
- 递归调用`countAndSay(n)`的最大深度是n,因此递归栈的空间复杂度是O(n)。
- 此外,在每一次递归调用中,我们使用一个StringBuilder来构建当前项的描述字符串,并返回它。这个StringBuilder的空间也是O(n)。
- 综上所述,总的空间复杂度是O(n)。
综合起来,该算法的时间复杂度是O(n^2),空间复杂度是O(n)。
LeetCode运行结果:
方法二:迭代
除了递归之外,我们还可以使用迭代的方法来生成外观数列。
public class Solution {public String countAndSay(int n) {String result = "1";for (int i = 2; i <= n; i++) {StringBuilder temp = new StringBuilder();int count = 1;for (int j = 0; j < result.length(); j++) {// 如果下一个字符与当前字符相同,则增加计数器if (j < result.length() - 1 && result.charAt(j) == result.charAt(j + 1)) {count++;} else { // 否则,将描述添加到临时字符串中,并重置计数器temp.append(count);temp.append(result.charAt(j));count = 1;}}result = temp.toString();}return result;}
}
在上面的代码中,我们使用一个循环从2到n,依次生成外观数列的每一项。对于每一项,我们使用一个临时的StringBuilder来构建它的描述字符串,并更新result变量为临时字符串的值。
复杂度分析:
这种迭代方法的时间复杂度和空间复杂度与递归方法相同,都是O(n^2)和O(n),因为我们仍然需要遍历前一项的描述字符串来计算当前项的描述字符串。只是在实现上,迭代方法更简单直观,没有递归的函数调用开销。
LeetCode运行结果:

方法三:动态规划
除了递归和迭代,还可以使用动态规划的方法来生成外观数列。动态规划通过存储中间结果来避免重复计算,提高效率。
public class Solution {public String countAndSay(int n) {List<String> dp = new ArrayList<>();dp.add("1"); // 初始项for (int i = 1; i < n; i++) {String prev = dp.get(i - 1); // 前一项的描述字符串StringBuilder current = new StringBuilder();int count = 1;for (int j = 0; j < prev.length(); j++) {// 如果下一个字符与当前字符相同,则增加计数器if (j < prev.length() - 1 && prev.charAt(j) == prev.charAt(j + 1)) {count++;} else { // 否则,将描述添加到临时字符串中,并重置计数器current.append(count);current.append(prev.charAt(j));count = 1;}}dp.add(current.toString()); // 将当前项的描述字符串添加到动态规划数组中}return dp.get(n - 1); // 返回第n项的描述字符串}
}
在上面的代码中,我们使用一个动态规划数组dp来存储每一项的描述字符串。初始时,将"1"作为第一项的描述字符串。然后,从2到n依次计算每一项的描述字符串,并将其存储到动态规划数组中。最后,返回第n项的描述字符串。
复杂度分析:
使用动态规划方法,我们将外观数列的每一项的描述字符串存储起来,避免了重复计算,提高了效率。它的时间复杂度仍然是O(n^2),但相对于递归和迭代方法,动态规划在计算过程中节省了一些中间计算的时间。空间复杂度为O(n),用来存储动态规划数组。
LeetCode运行结果:
方法四:递推
除了前面提到的方法,还可以使用递推方法来生成外观数列。递推方法是指根据已知的前几项,通过递推公式计算得到后续的项数。
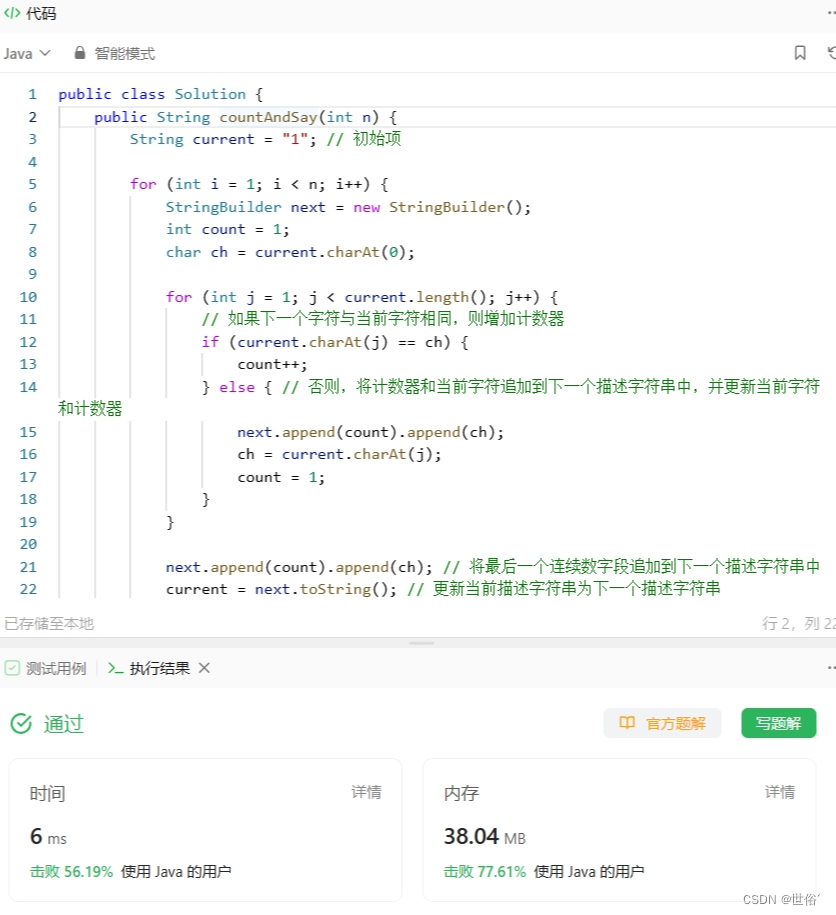
public class Solution {public String countAndSay(int n) {String current = "1"; // 初始项for (int i = 1; i < n; i++) {StringBuilder next = new StringBuilder();int count = 1;char ch = current.charAt(0);for (int j = 1; j < current.length(); j++) {// 如果下一个字符与当前字符相同,则增加计数器if (current.charAt(j) == ch) {count++;} else { // 否则,将计数器和当前字符追加到下一个描述字符串中,并更新当前字符和计数器next.append(count).append(ch);ch = current.charAt(j);count = 1;}}next.append(count).append(ch); // 将最后一个连续数字段追加到下一个描述字符串中current = next.toString(); // 更新当前描述字符串为下一个描述字符串}return current; // 返回第n项的描述字符串}
}
在这种方法中,我们根据外观数列的定义,通过递推公式计算每一项的描述字符串。具体来说,我们遍历当前项的描述字符串,记录当前字符和计数器。如果下一个字符与当前字符相同,则增加计数器;否则,将计数器和当前字符追加到下一个描述字符串中,并更新当前字符和计数器。最后,将最后一个连续数字段追加到下一个描述字符串中,更新当前描述字符串为下一个描述字符串。通过这种方式,我们可以递推得到所有项的描述字符串。
复杂度分析:
- 使用递推方法,我们避免了使用递归或动态规划来求解外观数列,减少了时间和空间复杂度。但是,递推方法需要根据递推公式,对每一项进行计算,因此时间复杂度仍然为O(n^2)。
- 空间复杂度为O(m),其中m是当前项的长度。在每次计算下一项时,我们只需使用一个StringBuilder对象来构建描述字符串,其长度为m。每次计算完成后,我们无需保留之前的计算结果,因此只需要恒定的额外空间来存储当前项的描述字符串。因此,总的空间复杂度为O(m)。
LeetCode运行结果:
相关文章:

怒刷LeetCode的第16天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:迭代 方法二:模拟 方法三:循环模拟 方法四:传递 第二题 题目来源 题目内容 解决方法 方法一:回溯 方法二:枚举优化 第三题 题目来源 题目…...
让大脑自由
前言 作者写这本书的目的是什么? 教会我们如何让大脑更好地为自己工作。 1 大脑的运行机制是怎样的? 大脑的基本运行机制是神经元之间通过突触传递信息,神经元的兴奋和抑制状态决定了神经网络的运行和信息处理,神经网络可以通过…...
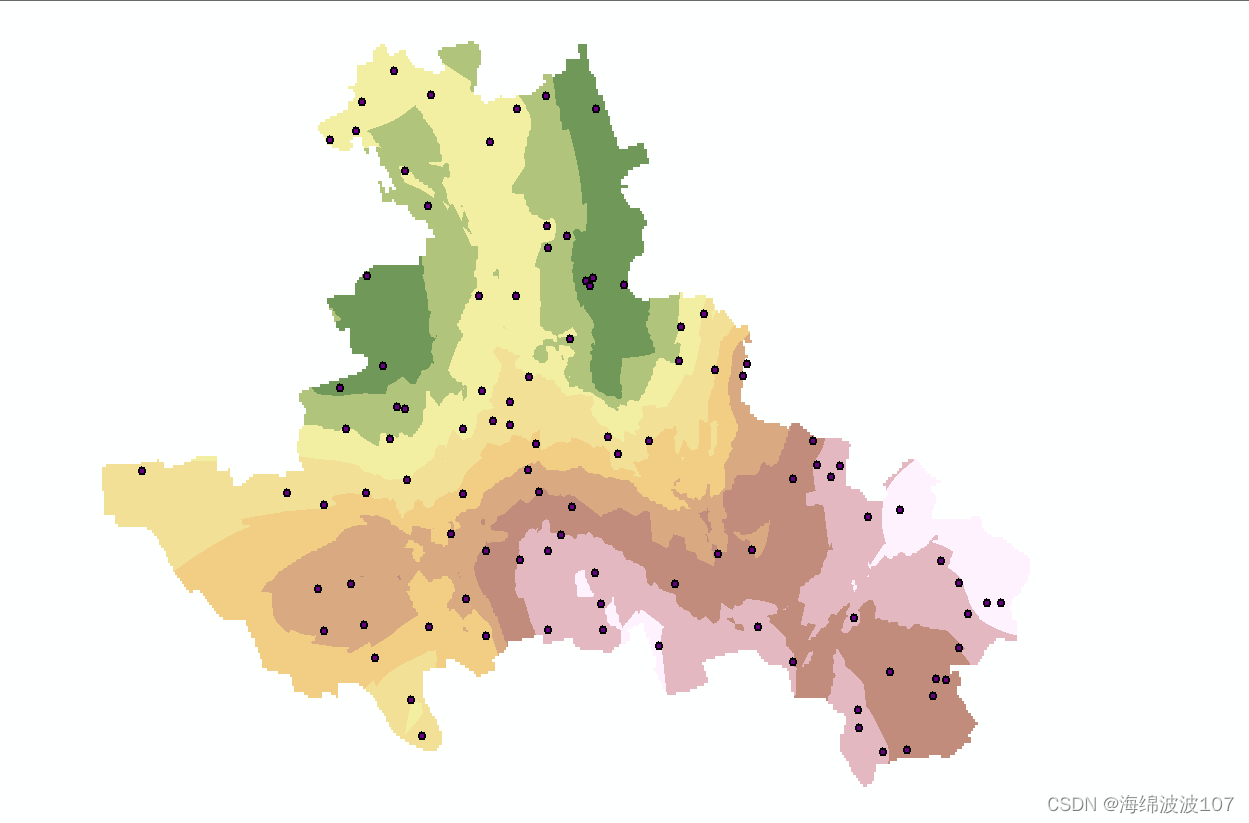
Arcgis克里金插值报错:ERROR 010079: 无法估算半变异函数。 执行(Kriging)失败。
Arcgis克里金插值报错:ERROR 010079: 无法估算半变异函数。 执行(Kriging)失败。 问题描述: 原因: shape文件的问题,此图可以看出,待插值的点有好几个都超出了地理范围之外,这个不知道是坐标系配准的问…...

Docker Compose安装
title: “Docker Compose安装” createTime: 2022-01-04T19:08:1508:00 updateTime: 2022-01-04T19:08:1508:00 draft: false author: “name” tags: [“docker”,“docker-compose”] categories: [“install”] description: “测试的” docker-compose安装步骤 1.下载 u…...
机器人过程自动化(RPA)入门 7. 处理用户事件和助手机器人
在UiPath中,有两种类型的Robot用于自动化任何流程。一个是后台机器人,它在后台工作。它独立工作,这意味着它不需要用户的输入或任何用户交互。另一个是前台机器人,也被称为助理机器人。 本章介绍前台机器人。在这里,我们将了解自动化过程中通过简单按键、单击鼠标等触发事…...

在linux下预览markdown的方法,转换成html和pdf
背景 markdown是一种便于编写和版本控制的格式,但却不便于预览——特别是包含表格等复杂内容时,单纯的语法高亮是远远不够的——这样就不能边预览边调整内容,需要找到一种预览方法。 思路 linux下有个工具,叫pandoc,…...
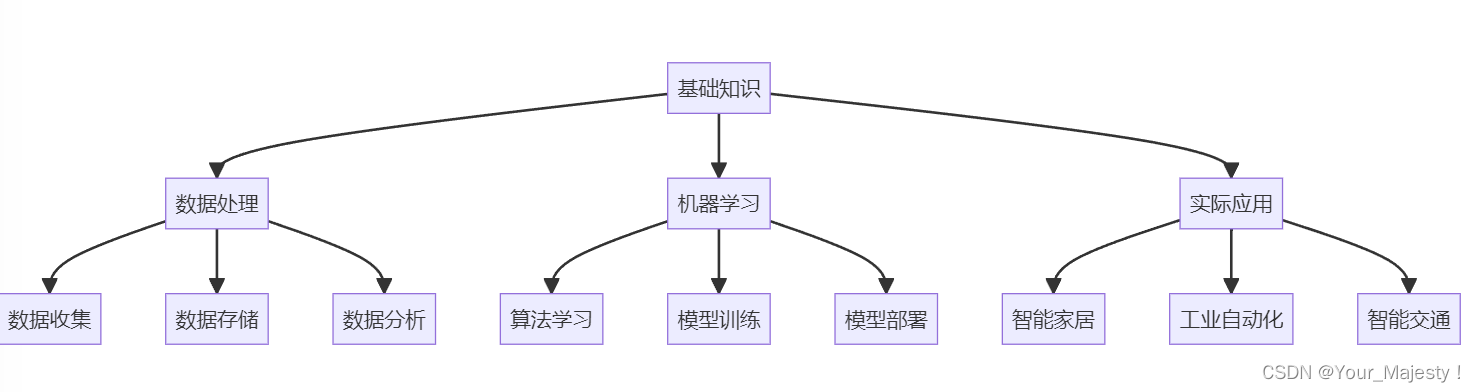
AIOT入门指南:探索人工智能与物联网的交汇点
AIOT入门指南:探索人工智能与物联网的交汇点 1. 引言 随着技术的快速发展,人工智能(AI)和物联网(IoT)已经成为当今最热门的技术领域。当这两个领域交汇时,我们得到了AIOT - 一个结合了AI的智能…...
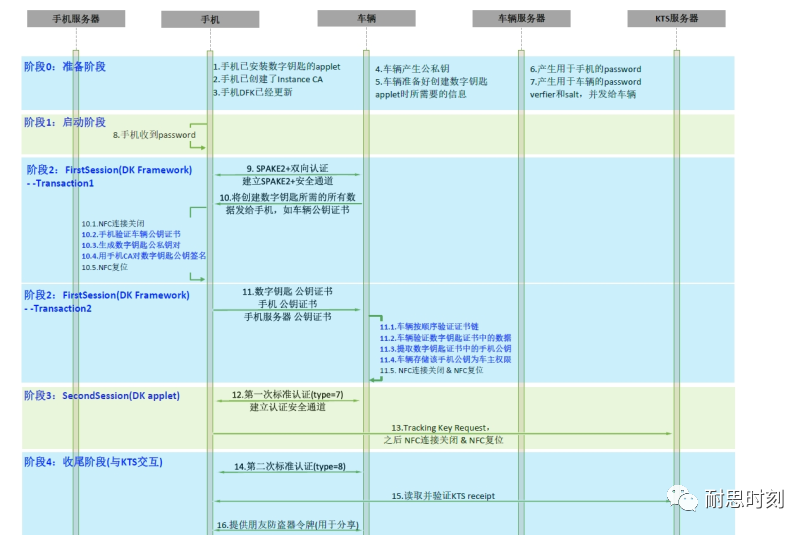
CCC数字钥匙设计【NFC】 --车主配对流程介绍
1、车主配对流程介绍 车主配对流程可以通过车内NFC进行,若支持UWB测距,也可以通过蓝牙/UWB进行,本文主要介绍通过NFC进行车主配对的流程。 整个配对流程相对较为复杂,本文主要梳理整体的步骤流程,其中的每个细节流程未…...
一站式开源持续测试平台 MerterSphere 之测试跟踪操作详解
一、MeterSphere平台介绍 MeterSphere是一站式的开源持续测试平台,遵循 GPL v3 开源许可协议,涵盖测试跟踪、接口测试、UI 测试和性能测试等功能,全面兼容JMeter、Selenium 等主流开源标准,有效助力开发和测试团队充分利用云弹性进…...

自然语言处理状况简介
一、说明 自然语言处理已经进入大模型时代,然而从业人员必须了解整个知识体系、发展过程、知识结构,应用范围等一系列知识。本篇将报道此类概况。 二、自然语言处理简介 自然语言处理,或简称NLP,是处理和转换文本的计算机科学学科…...
python爬虫基于管道持久化存储操作
文章目录 基于管道持久化存储操作scrapy的使用步骤1.先转到想创建工程的目录下:cd ...2.创建一个工程3.创建之后要转到工程目录下4.在spiders子目录中创建一个爬虫文件5.执行工程setting文件中的参数 基于管道持久化存储的步骤:持久化存储1:保…...

【MySQL】数据类型(二)
文章目录 一. char字符串类型二. varchar字符串类型2.1 char和varchar比较 三. 日期和时间类型四. enum和set类型4.1 set的查询 结束语 一. char字符串类型 char (L) 固定长度字符串 L是可以存储的长度,单位是字符,最大长度是255 MySQL中的字符ÿ…...

基于Matlab实现连续模型求解方法
本文介绍了如何使用Matlab实现连续模型求解方法。首先,我们介绍了连续模型的概念,并明确了使用ODE和PDE求解器来求解常微分方程和偏微分方程的步骤。然后,我们通过一个简单的例子演示了如何将问题转化为数学模型,并使用Matlab编写…...

Tomcat 与 JDK 对应版本关系
对应关系 Tomcat版本 jdk版本11.0.x JDK 21及以后10.1.x JDK11及以后10.0.xJDK1.8及以后9.0.x JDK1.8及以后8.5.xJDK1.7及以后8.0.x JDK1.7及以后 查看对应关系方法: 登陆Tomcat官网:Apache Tomcat - Welcome! 结果:...
iOS自动化测试方案(二):Xcode开发者工具构建WDA应用到iphone
文章目录 一、环境准备1.1、软件环境1.2、硬件环境1.3、查看版本 二、安装WDA过程2.7、构建失败,这类错误有很多,比如在选择开发者账号后,就会提示:Failed to register bundle identifier表示应用唯一注册失败2.9、第二个错误,完全…...
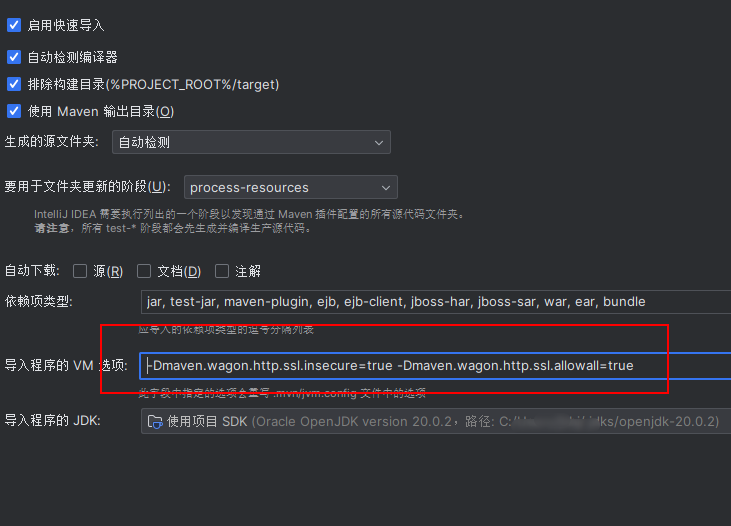
IDEA的Maven换源
前言 IDEA是个好东西,但是使用maven项目时可能会让人很难受,要么是非常慢,要么直接下载不了。所以我们需要给IDEA自带maven换源,保证我们的下载速度。 具体操作 打开IDEA安装路径,然后打开下面的文件夹 plugins\m…...
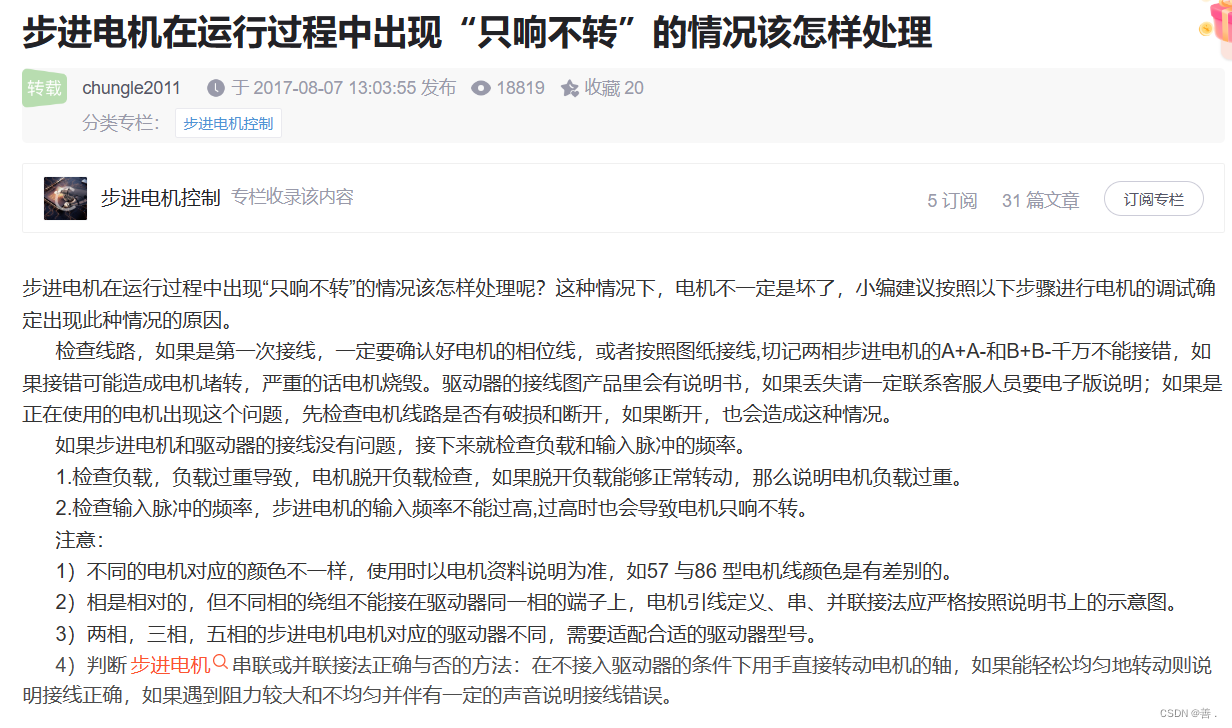
步进电机只响不转
我出现问题的原因是相位线接错。 我使用的滑台上示17H的步进电机,之前用的是57的步进电机。 57步进电机的相位线是A黑、A-绿、B红、B-蓝。 17步进电机的相位线是A红、A-绿、B黑、B-蓝。 这两天被一个问题困扰了好久,在调试步进电机开发板的时候电机发生…...

使用select实现服务器并发
select函数介绍: select 函数是一个用于在一组文件描述符上进行异步I/O多路复用的系统调用。它可以同时监视多个文件描述符,等待其中任何一个文件描述符准备就绪,然后进行相应的操作。 以下是select函数的原型: #include <…...
【Python】基于OpenCV人脸追踪、手势识别控制的求实之路FPS游戏操作
【Python】基于OpenCV人脸追踪、手势识别控制的求实之路FPS游戏操作 文章目录 手势识别人脸追踪键盘控制整体代码附录:列表的赋值类型和py打包列表赋值BUG复现代码改进优化总结 py打包 视频: 基于OpenCV人脸追踪、手势识别控制的求实之路FPS游戏操作 手…...

力扣 -- 718. 最长重复子数组
解题步骤: 参考代码: class Solution { public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m nums1.size();int n nums2.size();//多开一行,多开一列vector<vector<int>> dp(m 1, ve…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
