机器人中的数值优化|【四】L-BFGS理论推导与延伸
机器人中的数值优化|【四】L-BFGS理论推导与延伸
往期内容回顾
机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化,拟牛顿法理论与推导
L-BFGS方法
在上一节中我们对拟牛顿法进行了详细的推导,特别是对BFGS的推导过程比较熟悉了,我们发现BFGS虽然解决了牛顿法中hessian可能不存在以及hessian求逆计算复杂的通电,但是在大规模优化过程中,很可能没有办法去存储一个 n × n n \times n n×n矩阵,因此Limited memory GFGS算法自然而然就被提出,表示使用有限的空间来进行计算。观察原来的式子
Δ B t = Δ g t Δ g t T Δ x t Δ g t T − B t Δ x t Δ x t T B t T Δ x t T Δ B t T Δ x t \Delta B_t = \frac{\Delta g_t \Delta g_t^T}{\Delta x_t \Delta g_t^T} - \frac{B_t \Delta x_t \Delta x_t^T B_t^T}{\Delta x_t^T \Delta B_t^T \Delta x_t} ΔBt=ΔxtΔgtTΔgtΔgtT−ΔxtTΔBtTΔxtBtΔxtΔxtTBtT
B t + 1 − 1 = ( I n − Δ x Δ g T Δ x t T Δ g t ) B t − 1 ( I n − Δ g t Δ x t T Δ x t T Δ g t ) + Δ x t Δ x t T Δ x t T Δ g t B_{t+1}^{-1} = (I_n - \frac{\Delta x \Delta g^T}{\Delta x_t^T \Delta g_t})B_t^{-1}(I_n - \frac{\Delta g_t \Delta x_t^T}{\Delta x_t^T \Delta g_t}) + \frac{\Delta x_t \Delta x_t^T}{\Delta x_t^T \Delta g_t} Bt+1−1=(In−ΔxtTΔgtΔxΔgT)Bt−1(In−ΔxtTΔgtΔgtΔxtT)+ΔxtTΔgtΔxtΔxtT
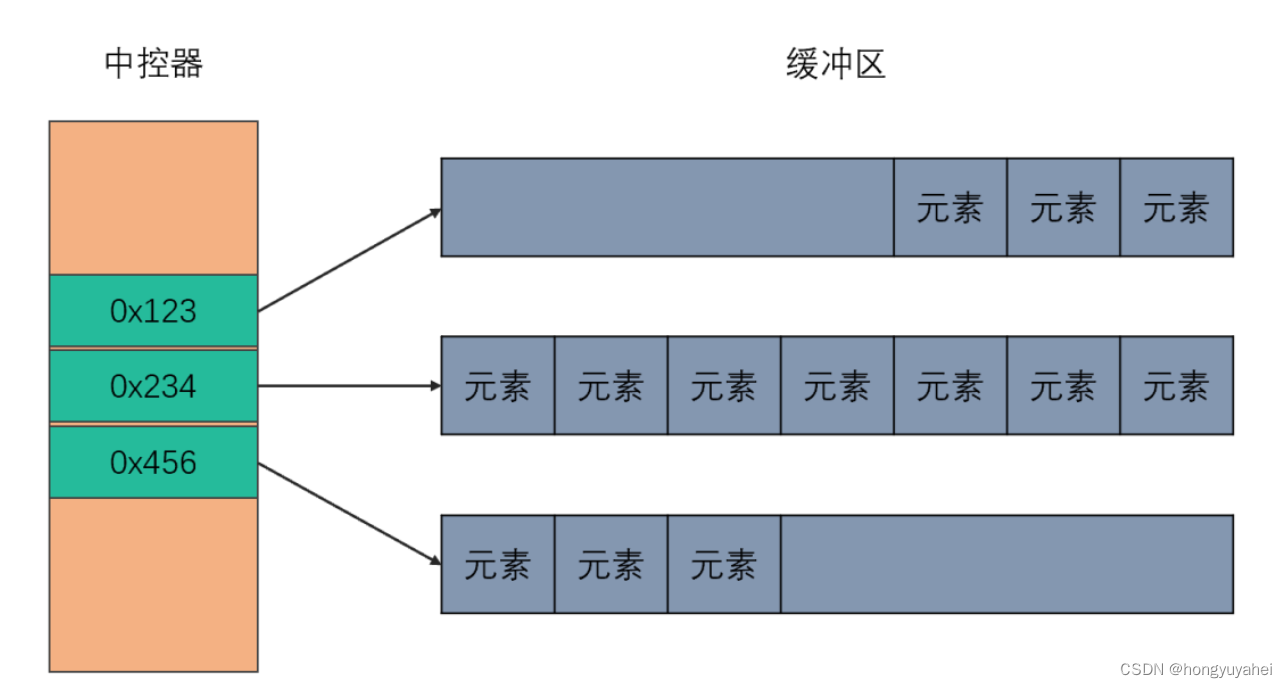
我们很容易知道, B t + 1 B_{t+1} Bt+1可以通过迭代计算 Δ x t , Δ g t \Delta x_t,\Delta g_t Δxt,Δgt来得到,LBFGS的思想是不再使用所有的 Δ x t , Δ g t \Delta x_t,\Delta g_t Δxt,Δgt,而是通过使用最近的 m m m个序列来计算。这样只需要保存 2 m 2m 2m个向量,然后每次迭代最近的结果即可计算出近似矩阵 B B B,避免显式保存矩阵信息。
令
ρ k = 1 Δ x k T Δ g k \rho_k = \frac{1}{\Delta x_k^T \Delta g_k} ρk=ΔxkTΔgk1
V k = I − ρ k Δ x k Δ g k T V_k = I -\rho_k \Delta x_k \Delta g_k^T Vk=I−ρkΔxkΔgkT
可以简写为
B t + 1 − 1 = V k B t − 1 V k T + ρ k Δ x t Δ x t T B_{t+1}^{-1} = V_kB_{t}^{-1}V_k^T + \rho_k \Delta x_t \Delta x_t^T Bt+1−1=VkBt−1VkT+ρkΔxtΔxtT
实际工程应用中,可以使用two-loop recursion方法,直接计算得到搜索方向,不用显示计算矩阵,如下所示:


相关文章:

机器人中的数值优化|【四】L-BFGS理论推导与延伸
机器人中的数值优化|【四】L-BFGS理论推导与延伸 往期内容回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例 机器人中的数值优化|【三】无约束优化,拟牛…...
ThemeForest – Canvas 7.2.0 – 多用途 HTML5 模板
ThemeForest 上的 HTML 网站模板受到全球数百万客户的喜爱。与包含网站所有页面并允许您在 WP 仪表板中自定义字体和样式的 WordPress 主题不同,这些设计模板是用 HTML 构建的。您可以在 HTML 编辑器中编辑模板,但不能在 WordPress 上编辑模板࿰…...

本地部署 川虎 Chat
本地部署 川虎 Chat 1. 川虎 Chat 项目概述2. Github 地址3. 部署 川虎 Chat4. 配置 config.json5. 启动 川虎 Chat 1. 川虎 Chat 项目概述 为ChatGPT等多种LLM提供了一个轻快好用的Web图形界面和众多附加功能。 支持 GPT-4 基于文件问答 LLM本地部署 联网搜索 Agent 助理…...
IntelliJ IDEA 控制台中文乱码的四种解决方法
前言 IntelliJ IDEA 如果不进行配置的话,运行程序时控制台有时候会遇到中文乱码,中文乱码问题非常严重,甚至影响我们对信息的获取和程序的跟踪。开发体验非常不好。 本文中我总结出四点用于解决控制台中文乱码问题的方法,希望有助…...

23岁准备转行嵌入式
前端难找工作,而且感觉没有前景,我觉得我就算入行也不会干多久,软件开发让我感觉不到实在的东西。小时候喜欢去动手制作一些玩具,我对实在一些的东西感兴趣一些例如手表,小机器人等等一些。我有保持坚持学习下去的动力…...

http请求报错:406 Not Acceptable的解决办法
目录 应用场景 基本概念 解决方法 方法一: 方法二: 方法三: 应用场景 接口在返回结果集的时候出现了406的报错,但是返回String类型不会报错,正常返回。 基本概念 406 Not Acceptable是一个HTTP响应状态码&…...

信息化发展75
数字化治理 数字化治理通常指依托互联网、大数据、人工智能等技术和应用,创新社会治理方法与手段,优化社会治理模式,推进社会治理的科学化、精细化、高效化,助力社会治理现代化。数字化治理是数字经济的组成部分之一,…...
C++八股
1、简述一下C中的多态 在面向对象中,多态是指通过基类的指针或引用,在运行时动态调用实际绑定对象函数的行为,与之相对应的编译时绑定函数称为静态绑定。 静态多态 静态多态是编译器在编译期间完成的,编译器会根据实参类型来选择…...

Nat. Commun. | 大规模高分辨单光子成像
本文由论文作者团队(课题组)投稿 单光子雪崩二极管(Single Photon Avalanche Diode,简称SPAD)阵列因其极佳的单光子灵敏度而受到广泛关注,已广泛应用于量子通信与计算、荧光寿命成像、时间飞行成像等各个领域。与同样具有较高灵敏度的EMCCD和sCMOS相比,SPAD阵列能够在极…...

Android开源库
见:GitHub - eHackyd/Android_OpenSourceLibrary: Android开源库的学习笔记...

【小程序 - 基础】页面导航、页面事件、生命周期、WXS脚本_04
目录 一、页面导航 1. 什么是页面导航 2. 小程序中实现页面导航的两种方式 2.1 声明式导航 2.1.1 导航到 tabBar 页面 2.1.2 导航到非 tabBar 页面 2.1.3 后退导航 2.2 编程式导航 2.2.1 导航到 tabBar 页面 2.2.2 导航到非 tabBar 页面 2.2.3 后退导航 2.3. 导航…...

矩阵求导数
矩阵 A ∣ 1 2 1 2 − 1 3 ∣ , 计算 f ( x ) ∣ ∣ A x ∣ ∣ 2 ∣ ∣ x ∣ ∣ 2 的最大值。 矩阵A \begin {vmatrix} 1 & 2 & 1\\2 & -1 & 3 \end {vmatrix},计算f(x) \frac{||Ax||_2}{||x||_2}的最大值。 矩阵A 122−113 ,计算f(x)∣∣x∣∣2…...
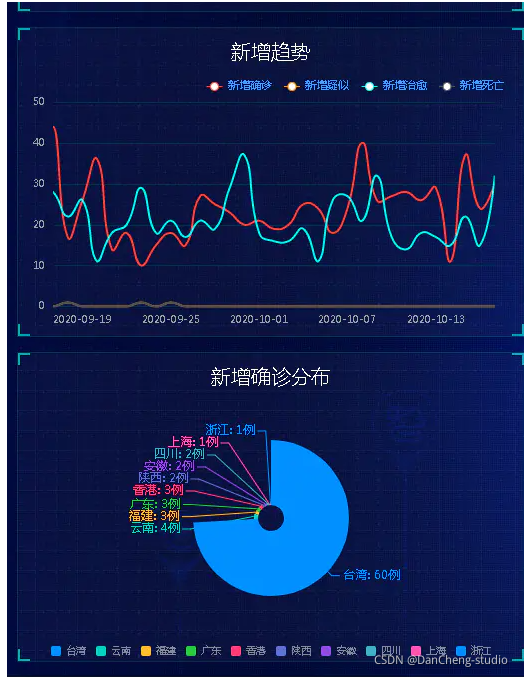
竞赛 大数据疫情分析及可视化系统
文章目录 0 前言2 开发简介3 数据集4 实现技术4.1 系统架构4.2 开发环境4.3 疫情地图4.3.1 填充图(Choropleth maps)4.3.2 气泡图 4.4 全国疫情实时追踪4.6 其他页面 5 关键代码最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 大数据疫…...
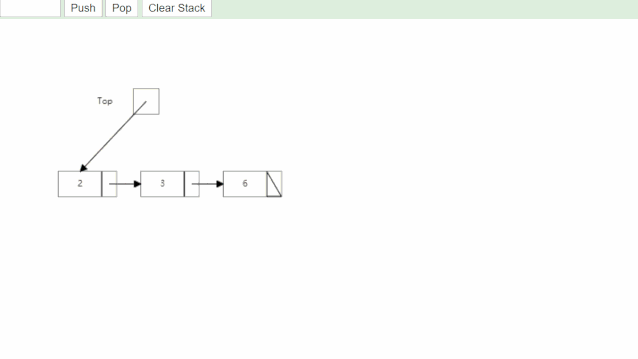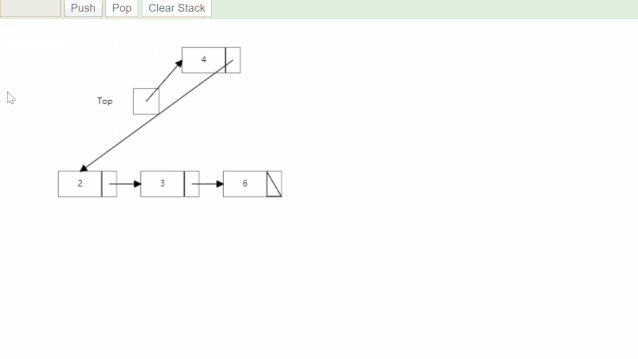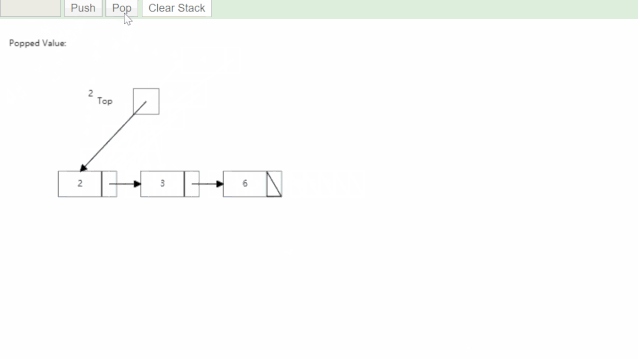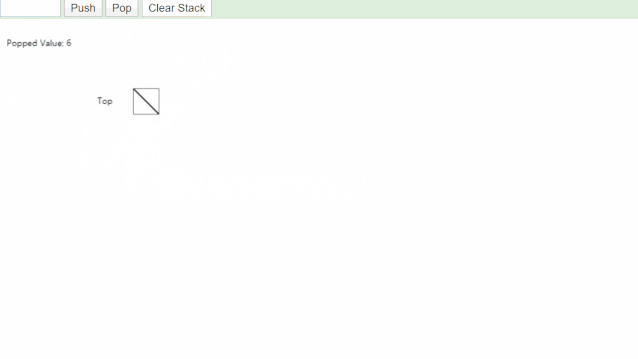
数据结构--栈
线性表的定义 前面文章有讲过,线性表就是一次保存单个同类型元素,多个元素之间逻辑上连续 例子:数组,栈,队列,字符串 栈 1.1 栈和队列的特点 栈和队列都是操作受限的线性表。 前面学过的数组,…...
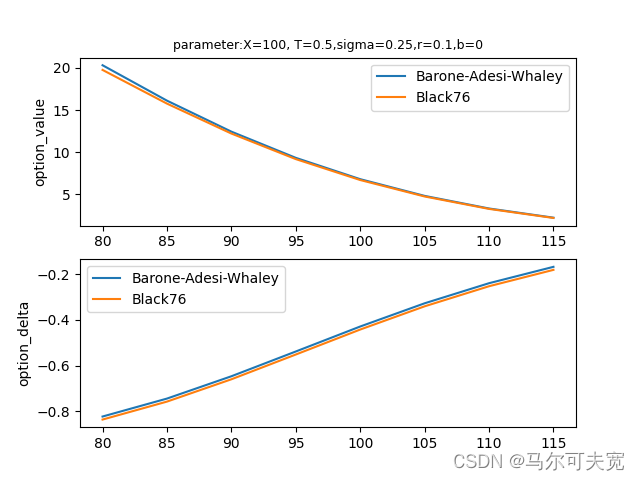
期权定价模型系列【7】:Barone-Adesi-Whaley定价模型
期权定价模型系列第7篇文章 1.前言 目前大连商品交易所、郑州商品交易所、以及上海期货交易所的所有商品期权都为美式期权,并且大商所的所有期权合约会根据BAW(Barone-Adesi-Whaley)美式期权定价模型计算新上市期权合约的挂牌基准价。 BAW模型(Barone-Adesi and W…...
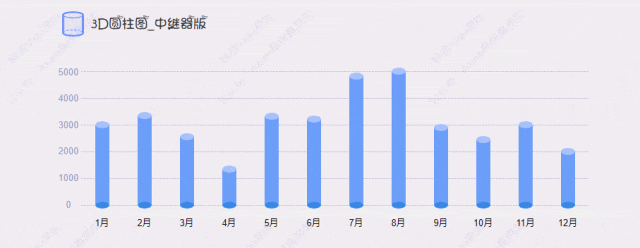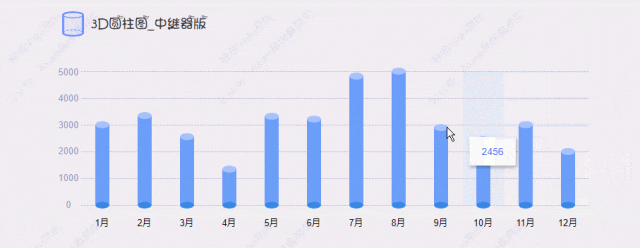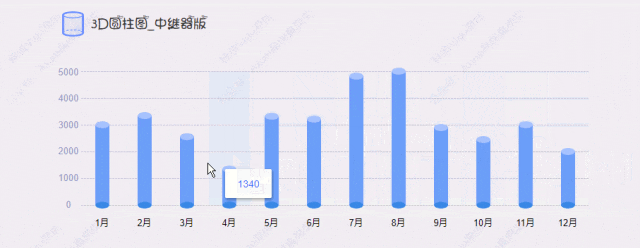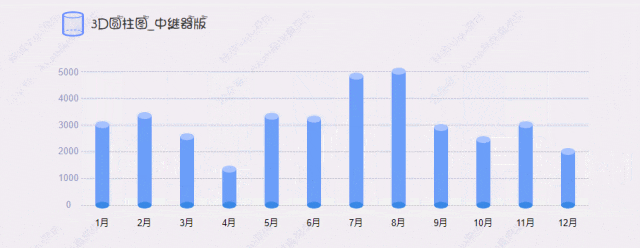
【Axure高保真原型】3D圆柱图_中继器版
今天和大家分享3D圆柱图_中继器版的原型模板,图表在中继器表格里填写具体的数据,调整坐标系后,就可以根据表格数据自动生成对应高度的圆柱图,鼠标移入时,可以查看对应圆柱体的数据……具体效果可以打开下方原型地址体验…...

多个线程启动 ,等待全部执行完毕再搜集数据
前几天在公司的项目上有个同事使用了多线程统计数据,当时出现了一个用户一直使用服务器首次登录信息作为查询信息。找了半天才发现,线程池资源同步了。后面手动将数据set进去的。 等待线程全部执行完毕,这里使用的是减法计数器,也…...

【VIM】VIm-plug插件
如何查找需要的插件 https://github.com/mhinz/vim-startify https://github.com/vim-airline/vim-airline https://github.com/Yggdroot/indentLine github.com/w0ng/vim-hybrid github.com/altercationi/vim-colors-solarized guithub.com/morhetz/gruvbox github.com/sc…...
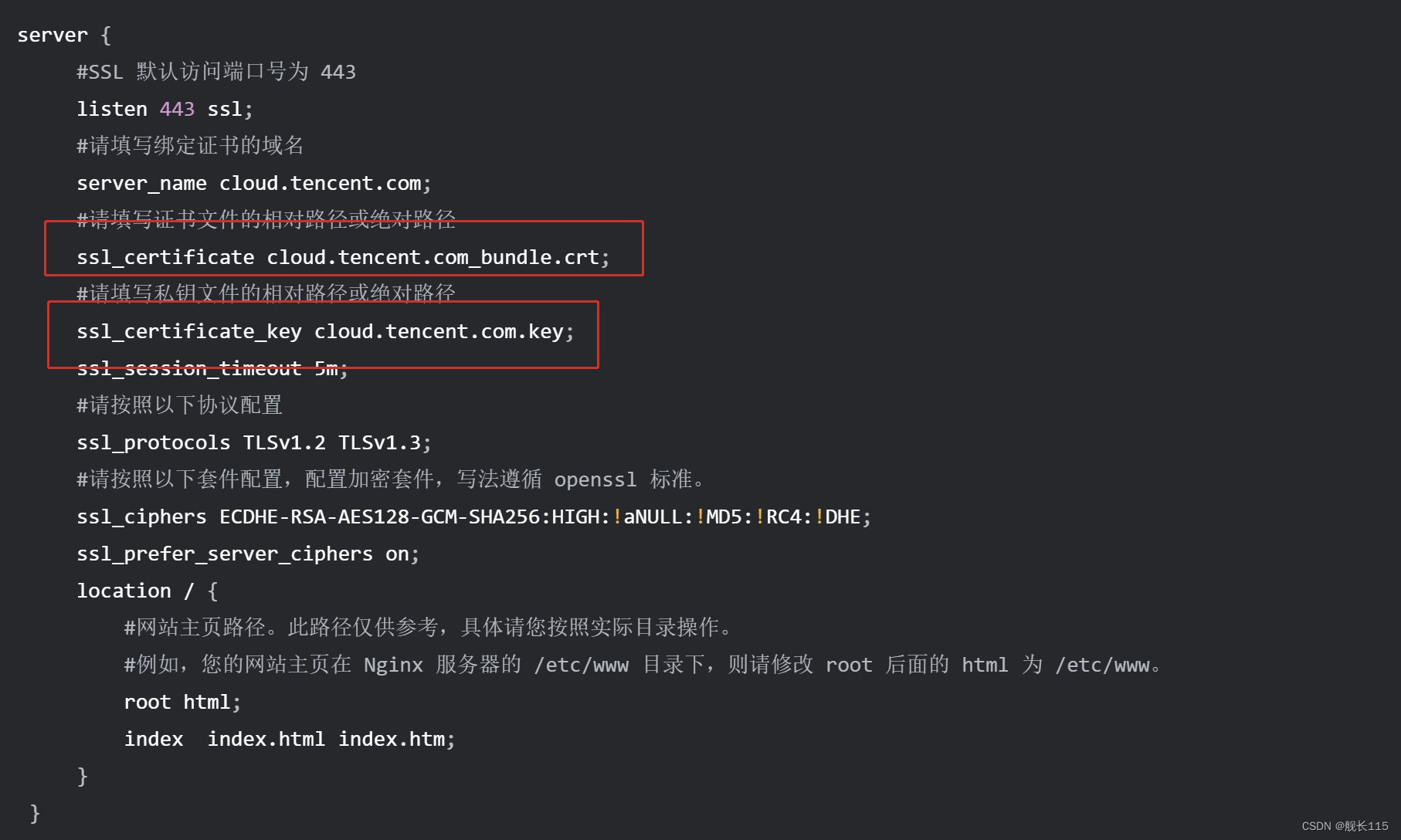
ssl证书 阿里的域名,腾讯云的证书
目录 1.腾讯云申请ssl免费证书 2.去阿里云进行解析 3.回到腾讯云 4.nginx的配置 说明:阿里云的免费证书用完了(每年可以申请20个),还有个项目要用证书,第三方的证书免费的都是90天的。看了下腾讯云业可以申请免费的…...

力扣算法题:34、在排序数组中查找元素的第一个和最后一个位置.java版
版本说明 当前版本号[20230930]。 版本修改说明20230930初版 34.在排序数组中查找元素的第一个和最后一个位置 34. 在排序数组中查找元素的第一个和最后一个位置 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
