RSA算法
算法简介
RSA是一种非对称加密方式。发送者把明文通过公钥加密后发送出去,接受者把密文通过私钥解密得到明文。
算法过程
生成公钥和私钥
选取两个质数p和q,n=p*q。n的长度就是密钥长度。
φ(n)=(p-1)*(q-1)
φ(n)为n的欧拉函数。
找到1-φ(n)间与φ(n)互质的一个数 e,将n和e封装成公钥。
d*e ≡ 1(mod φ(n)),将n和d封装成私钥。
加密过程
假设明文为X
密文 Y=X^e mod N
解密过程
X = Y^d mod N
算法的可靠性
上述加解密过程一共涉及6个数字:
n p q φ(n) e d
公钥 n e 私钥 n d。算法的可靠性即在已知 n和e的情况下能否推出d。
ed ≡ 1(mod φ(n)) 只有知道e和φ(n) 才能得出d
φ(n)=(p-1)*(q-1) 只有知道p和q才能得出φ(n)
n=p*q 只有将n因数分解 才能得到p和q
算法可靠性在于n因数分解,由于大数的因数分解是指数级别复杂程度,所以保证了加密算法的可靠性。
由RSA算法中大数因数分解复杂程度的延伸
大数分解因数为何困难
分解因数是把合数分解为非平凡解(非平凡解:排除1和本身的质因数)。
常规的因数分解 就是判断这个数能否被某一个质数整除,即 a%b==0。
求余的过程其实是用到了除法。除数较小的情况下,求余不是难事。但是当除数很大时,类似高精度除以高精度,除法的效率就不那么高了。
个人认为,计算机在处理大数的除法效率问题导致了大数分解因数困难。
计算机是如何处理除法运算
计算机的四则运算
传统的数学思维里并不能直接用在计算机的四则运算中,例如加法,13+29=42,传统思维直接对位相加,有进位再加上进位。这种思维对应计算机的处理就要用到异或运算,与运算,和左移运算。
13 的二进制 0000 1101
29 的二进制 0001 1101
异或运算 :处理0+1的情况
0000 1101 ⊕ 0001 1101 = 0001 0000 ①
与运算:处理1+1的情况,有1代表需要进位,
0000 1101 & 0001 1101 = 0000 1101
左移运算:非全0就需要左移
0000 1101 << 1 = 0001 1010 ②
用 ①、②重复异或运算、与运算、左移运算
0001 0000 ⊕ 0001 1010 = 0000 1010 ③
0001 0000 & 0001 1010 = 0001 0000
0001 0000 << 1 = 0010 0000 ④
处理 ③ ④
0000 1010 ⊕ 0010 0000 = 0010 1010 ⑤
0000 1010 & 0010 0000 = 0000 0000 ⑥
因为⑥结果全为0,所以 ⑤ 就是最终答案。 ⑤ 转为10进制即2^5+2^3+2^1 = 32+8+2=42。
计算机除法结论
减法就是用补码参与加法运算,乘法就是多个加法运算,本次讨论的除法就是不断地减法操作。所以大数的除法就涉及到不断地异或、与、左移运算导致运算复杂程度升高。
本文由 mdnice 多平台发布
相关文章:

RSA算法
算法简介 RSA是一种非对称加密方式。发送者把明文通过公钥加密后发送出去,接受者把密文通过私钥解密得到明文。 算法过程 生成公钥和私钥 选取两个质数p和q,np*q。n的长度就是密钥长度。φ(n)(p-1)*(q-1)φ(n)为n的欧拉函数。找到1-φ(n)间与φ(n)互质的…...

计算机竞赛 深度学习手势识别 - yolo python opencv cnn 机器视觉
文章目录 0 前言1 课题背景2 卷积神经网络2.1卷积层2.2 池化层2.3 激活函数2.4 全连接层2.5 使用tensorflow中keras模块实现卷积神经网络 3 YOLOV53.1 网络架构图3.2 输入端3.3 基准网络3.4 Neck网络3.5 Head输出层 4 数据集准备4.1 数据标注简介4.2 数据保存 5 模型训练5.1 修…...

Spring的Ordered
Ordered Java中的Ordered接口是Spring框架中的一个接口,用于表示对象的顺序。它定义了一个方法getOrder(),用于获取对象的顺序值,值越小的对象越先被处理。 Ordered接口是Spring框架中的一个接口,用于定义组件的加载顺序。当一个…...

前端两年半,CSDN创作一周年
文章目录 一、机缘巧合1.1、起因1.2、万事开头难1.3、 何以坚持? 二、收获三、日常四、憧憬 五、总结 一、机缘巧合 1.1、起因 最开始接触CSDN,还是因为同专业的同学,将计算机实验课的实验题,记录总结并发在了专业群里。后来正式…...

定时任务管理平台青龙 QingLong
一、关于 QingLong 1.1 QingLong 介绍 青龙面板是支持 Python3、JavaScript、Shell、Typescript 多语言的定时任务管理平台,支持在线管理脚本和日志等。其功能丰富,能够满足大部分需求场景,值得一试。 主要功能 支持多种脚本语言…...

java多线程相关介绍
1. 线程的创建和启动 在 Java 中创建线程有两种方式。一种是继承 Thread 类并重写其中的 run() 方法,另一种是实现 Runnable 接口并重写其中的 run() 方法。创建完线程对象后,调用 start() 方法可以启动线程。 2. 线程的状态 Java 的线程在不同阶段会处于…...

css复合选择器
交集选择器 紧紧挨着 <template><div><p class"btn">Click me</p><button class"btn" ref"myButton" click"handleClick">Click me</button></div> </template> <style> but…...
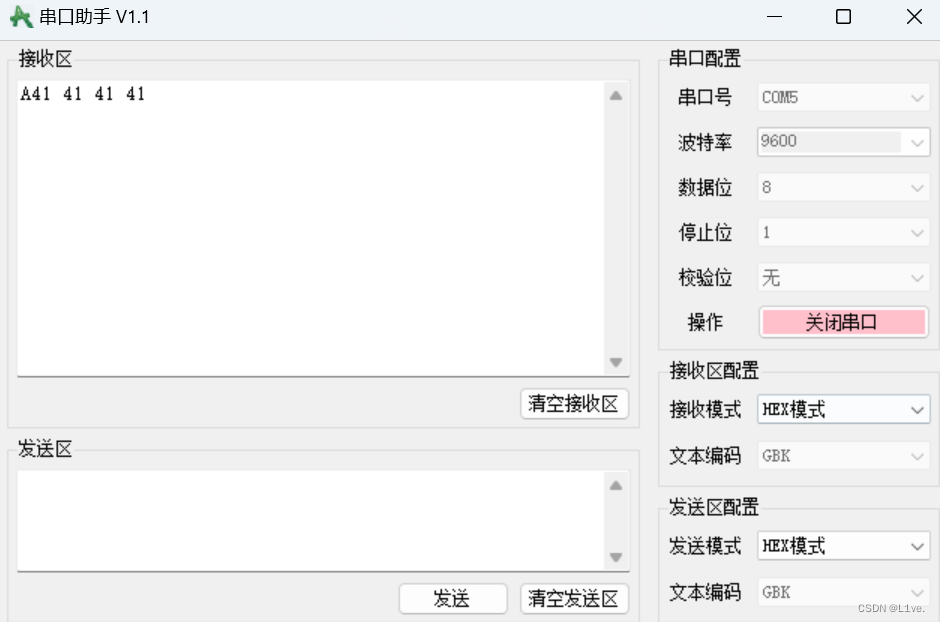
USART串口协议
通信接口 •通信的目的:将一个设备的数据传送到另一个设备,扩展硬件系统 • 通信协议:制定通信的规则,通信双方按照协议规则进行数据收发 全双工:指通信双方能够同时进行双向通信,一般来说,全双…...

picoctf_2018_shellcode
picoctf_2018_shellcode Arch: i386-32-little RELRO: Partial RELRO Stack: No canary found NX: NX disabled PIE: No PIE (0x8048000) RWX: Has RWX segments32位,啥都没开 这个看着挺大的,直接来个ROPchain,…...
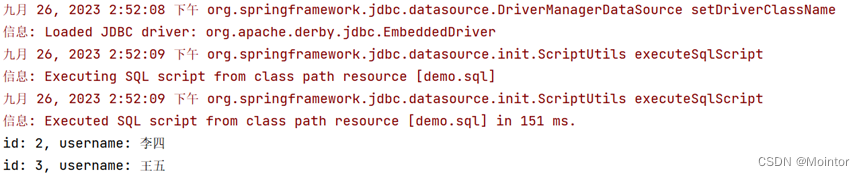
Apache Derby的使用
Apache Derby是关系型数据库,可以嵌入式方式运行,也可以独立运行,当使用嵌入式方式运行时常用于单元测试,本篇我们就使用单元测试来探索Apache Derby的使用 一、使用IDEA创建Maven项目 打开IDEA创建Maven项目,这里我…...

leetcode 图相关的题
图 图相关知识有leetcode207课程表1(有环判断)以及210 课程表2(拓扑排序). 链表遍历 def dfs(n):print(n)dfs(n)二叉树遍历 def dfs(n):print(n)dfs(n.left)dfs(n.right)多叉树遍历 dfs(root) def dfs(n):for node in n.nodes:dfs(node)图遍历 visited [False] * n_node…...

程序员们,我们能工作到65岁吗?
软件开发人员的职业生涯可以持续多久?这是大多数认真考虑成为专业程序员的人不禁想知道的事情。 在谈论这样一个要求很高的职业时,这是一个非常自然的问题。没有人愿意花费数年时间学习一项技能,这些技能将在几年内不再相关,或者当…...
)
【洛谷 P1996】约瑟夫问题 题解(队列+模拟+循环)
约瑟夫问题 题目描述 n n n 个人围成一圈,从第一个人开始报数,数到 m m m 的人出列,再由下一个人重新从 1 1 1 开始报数,数到 m m m 的人再出圈,依次类推,直到所有的人都出圈,请输出依次出圈人的编号。…...
字符串函数与内存函数讲解
文章目录 前言一、字符串函数1.求字符串长度strlen 2.长度不受限制的字符串函数(1)strcpy(2)strcat(3)strcmp 3.长度受限制的字符串函数(1)strncpy(2)strncat(3)strncmp 4.字符串查找(1)strstr(2)strtok 5.错误信息报告(1)strerror(2)perror 二、内存函数1.memcpy2.memmove3.me…...
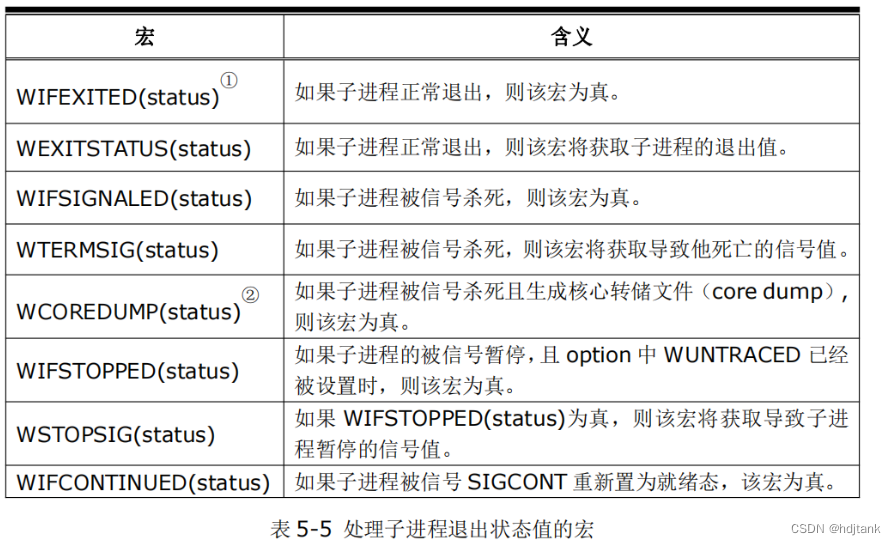
c语言系统编程之多进程
程序与进程的区别? 程序是静态的未运行的二进制文件,存储在磁盘中 进程是已经运行的二进制文件,存储在内存中 进程的内存划分图有哪几部分? 堆(存储malloc和calloc出来的空间)、栈(局部变量…...

前端还是后端:探讨Web开发的两大街区
前端还是后端:探讨Web开发的两大街区 一、引言二、两者的对比分析技能要求和专业知识职责和工作内容项目类型和应用领域就业前景和市场需求 三、技能转换和跨领域工作四、全栈开发结语 一、引言 Web开发领域涉及到前端开发和后端开发这两个不同而又互为补充的领域。…...

JavaScript中如何确定this的值?如何指定this的值?
🎀JavaScript中的this 在绝大多数情况下,函数的调用方法决定了this的值(运行时绑定)。this不能在执行期间被赋值,并且在每次函数呗调用时this的值也可能会不同。 🍿如何确定this的值: 在非严格…...
ubuntu下源码编译方式安装opencv
基础条件 ubuntu 20.04 opencv 3.4.3 opencv 源码编译的安装步骤 第一步, 首先clone源码 git clone https://github.com/opencv/opencv.git第二步,依赖包,执行下面的命令 sudo apt-get install build-essential sudo apt-get install cmak…...

spring boot整合常用redis客户端(Jedis、Lettuce、RedisTemplate、Redisson)常见场景解决方案
Java操作redis有三种客户端供选择:Jedis、Lettuce、Redisson。 在实际项目中运用最多的客户端还是Redisson、RedisTemplate;其中RedisTemplate并非是一个新的redis客户端实现,RedisTemplate是Spring Data Redis中提供的封装好的redis操作模板…...

HarmonyOS之运行Hello World
目录 下载与安装DevEco Studio 配置环境 创建项目 认识DevEco Studio界面 运行Hello World 了解基本工程目录 工程级目录 模块级目录...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
