【C语言数据结构——————栈和队列4000字详解】
欢迎阅读新一期的c语言数据结构模块————栈和队列
✒️个人主页:-_Joker_-
🏷️专栏:C语言
📜代码仓库:c_code
🌹🌹欢迎大佬们的阅读和三连关注,顺着评论回访🌹🌹
文章目录
- 栈
- 一、栈的概念
- 1.什么是栈
- 2.栈的基本操作
- 二、栈的实现
- 1.定义栈的结构
- 2.栈的初始化
- 3.栈的判空
- 4.入栈
- 5.出栈
- 6.获取栈顶元素
- 7.栈的销毁
- 一、栈的概念
- 队列
- 一、队列的概念
- 1.什么是队列
- 2.队列的基本操作
- 二、队列的实现
- 1.定义队列的结构
- 2.队列初始化
- 3.队列判空
- 4.入队
- 5.出队
- 6.获取队首元素
- 7.队列的销毁
- 一、队列的概念
栈
一、栈的概念
1.什么是栈
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。

栈顶(Top): 线性表允许进行插入删除的那一端。
栈底(Bottom): 固定的,不允许进行插入和删除的另一端。
空栈: 不含任何元素的空表。
因为其后进先出(Last In First Out)的特性,栈又称为的线性表,简称LIFO结构
2.栈的基本操作
栈的基本操作通常都有以下几种:
- InitStack(&Stack):初始化一个空栈S。
- StackEmpty(&Stack):判断一个栈是否为空,若栈为空则返回true,否则返回false。
- StackPush(&Stack, x):进栈(栈的插入操作),若栈S未满,则将x加入使之成为新栈顶。
- StackPop(&Stack):出栈(栈的删除操作),若栈S非空,则返回一个提示.
- GetTop(&Stack):读栈顶元素。
- DestroyStack(&Stack):栈销毁,并释放S占用的存储空间(“&”表示引用调用)。
二、栈的实现
1.定义栈的结构
栈又分为顺序栈和链式栈,这里我们以顺序栈为例
首先想要实现一个栈,我们需要了解如何创建一个栈的结构,这里我们可以用结构体来定义,有两种方式:
①
#define N 10//定义栈的大小
struct Stack
{int a[N];int top;//栈顶
};②
typedef int STDataType;
typedef struct Stack
{STDataType* a;//定义一个栈int top;//栈顶int capacity;//栈的大小
}ST;第一种结构是用一个宏定义常量定义的栈的大小,这种用静态开辟的空间存在一些瑕疵,如果栈的空间大小太小需要成倍的扩容,很容易造成空间的浪费,所以我们优先采用方法②。
这种方法的好处在于我们可以动态开辟空间,如果空间不够就多开一个空间,这样就可以避免空间的浪费。
2.栈的初始化
void InitStack(ST* ps)
{assert(ps);//断言ps->a = NULL;//将指针置为空ps->capacity = 0;//初始化大小ps->top = 0;
}3.栈的判空
bool StackEmpty(ST* ps)
{assert(ps);//断言return ps->top == 0;//栈顶为0则为空
}4.入栈
入栈的具体流程如图
入栈首先判断空间大小,若已满则需要扩容,然后从栈底向上逐个插入
入栈操作如下
void StackPush(ST* ps, STDataType x)
{assert(ps);//断言if (ps->top == ps->capacity){int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newCapacity);//扩容 if (tmp == NULL)//判断空间是否开辟成功{perror("realloc fail");exit(-1);}ps->a = tmp;ps->capacity = newCapacity;}ps->a[ps->top] = x;//插入元素ps->top++;//栈顶移动
}
5.出栈
出栈操作如图
出栈首先判断是否为空,若为空则返回一个提示,若不为空则只需要直接将栈顶向下移动即可达到出栈的效果。
出栈操作如下;
void StackPop(ST* ps)
{assert(ps);//断言assert(ps->top > 0);//判断空--ps->top;//栈顶移动
}6.获取栈顶元素
这里需要注意top的位置,如果top的指向是栈顶元素的话则只需要return a[ps->top]即可,由于我这里的top是指向栈顶元素的下一个位置,所以需要top-1才可以获取到栈顶元素.
STDataType StackTop(ST* ps)
{assert(ps);assert(ps->top > 0);//判断为空return ps->a[ps->top - 1];//返回栈顶元素
}7.栈的销毁
void StackDestroy(ST* ps)
{assert(ps);free(ps->a);//释放栈的空间ps->a = NULL;//将指针置空,防止野指针产生ps->top = ps->capacity = 0;
}队列
一.队列的概念
1.什么是队列
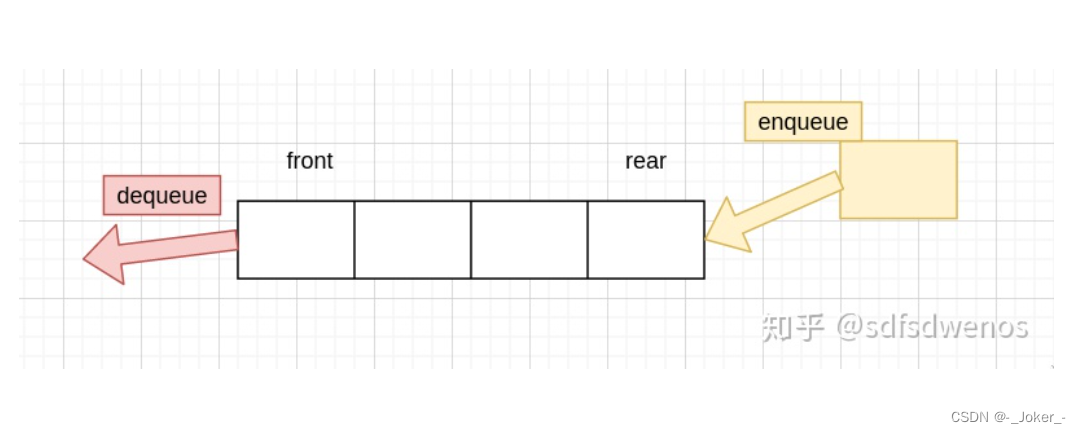
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
队首(front): 线性表允许进行插入删除的那一端。
队尾(rear): 固定的,不允许进行插入和删除的另一端。
空队列: 不含任何元素的空表。
因为其先进先出(First In First Out)的特性,队列又称为的线性表,简称FIFO结构
2.队列的基本操作
- QueueInit(&Q):初始化队列,构造一个空队列Q。
- QueueEmpty(Q):判队列空,若队列Q为空返回true,否则返回false。
- QueuePush(&Q, x):入队,若队列Q未满,将x加入,使之成为新的队尾。
- QueuePop(&Q):出队,若队列Q非空,删除队头元素。
- QueueFront(&Q):读队头元素。
- QueueDestroy(&Q): 队列销毁。
二.队列的实现
队列同样拥有两种实现方式(顺序结构和链式结构),但是用顺序结构实现队列在出列的情况比较复杂,所以这里我们以链式结构来实现队列
1.定义队列的结构
和栈类似,队列的结构可以这样定义
typedef int QDataType;
typedef struct QueueNode//队列节点
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue//队列结构
{QNode* head;//队首QNode* tail;//队尾int size;
}Que;2.队列初始化
void QueueInit(Que* pq)
{assert(pq);//断言pq->head = pq->tail = NULL;//头尾指针置空pq->size = 0;//大小初始化
}3.队列判空
bool QueueEmpty(Que* pq)
{assert(pq);//断言return pq->head == NULL;//头指针为空则为空
}4.入队
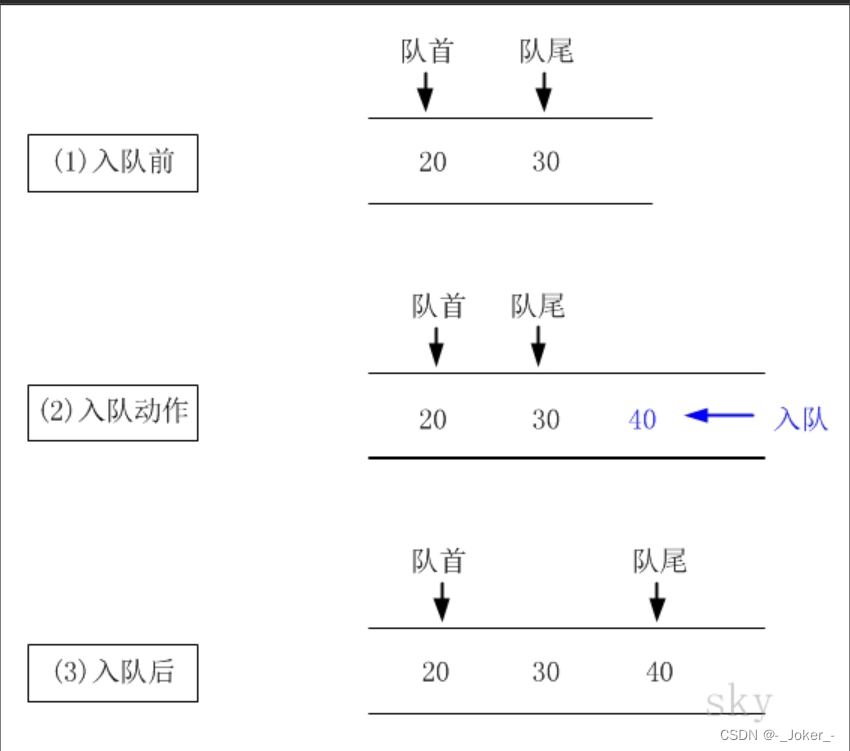
入队操作如图
入队新开一个节点,将元素插入新的节点,然后判断尾指针是否指向空,若为空则将头尾指针指向新的节点,若不为空则将新的节点作为队尾。
入队实现:
void QueuePush(Que* pq, QDataType x)
{assert(pq);//断言QNode* newnode = (QNode*)malloc(sizeof(QNode));//开一个新节点if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;//新节点赋值newnode->next = NULL;if (pq->tail == NULL)//空队列{pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}5.出队
出队操作和入队操作类似,出队首先判空,若队列为空则返回一个提示,若不为空需要将队首节点指向下一个节点并释放第一个节点。若队首的下一个元素为空,说明改队列只有一个节点,所以需要将头尾指针置空防止野指针的产生。
出队操作如下
void QueuePop(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));//判空if (pq->head->next == NULL)//判断队首下一个节点是否为空{free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;//新开一个节点并将头指针下一个节点给新节点free(pq->head);//释放队首pq->head = next;//将新开的节点赋给新队首}pq->size--;//队列大小-1
}
6.读取队首元素
QDataType QueueFront(Que* pq)
{assert(pq);assert(!QueueEmpty(pq));//判空return pq->head->data;//取队首元素
}7.队列销毁
void QueueDestroy(Que* pq)
{assert(pq);QNode* cur = pq->head;//创建一个节点存储队首while (cur)//{QNode* next = cur->next;//创建一个中间节点free(cur);//从队首一个一个删除cur = next;}pq->head = pq->tail = NULL;//删完所有节点将指针置空pq->size = 0;//初始化大小
}以上就是栈和队列的基本概念和基础操作实现,如果文章存在错误请在评论区留言,最后别忘了三连支持一下,顺着评论回访🌹🌹
相关文章:
【C语言数据结构——————栈和队列4000字详解】
欢迎阅读新一期的c语言数据结构模块————栈和队列 ✒️个人主页:-_Joker_- 🏷️专栏:C语言 📜代码仓库:c_code 🌹🌹欢迎大佬们的阅读和三连关注,顺着评论回访🌹&#…...
电子地图 | VINS-FUSION | 小觅相机D系列
目录 一、相关介绍 二、VINS-FUSION环境安装及使用 (一)Ubuntu18.04安装配置 1、Ubuntu下载安装 2、设置虚拟内存(可选) (二)VINS-FUSION环境配置 1、ros安装 2、ceres-solver安装 3、vins-fusion…...
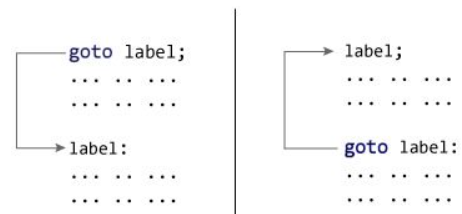
C++goto语句
在本文中,您将了解goto语句,它是如何工作的,以及为什么应该避免它。在C 编程中,goto语句用于通过将控制权转移到程序的其他部分来更改程序执行的正常顺序。 goto语句的语法 goto label; ... .. ... ... .. ... ... .. ... label…...
Spring学习笔记11 GoF代理模式
Spring学习笔记10 JdbcTemplate_biubiubiu0706的博客-CSDN博客 新建个maven模块 static-proxy 演示静态代理 订单接口 测试 需求:统计每个业务方法的耗时 package com.example.proxy.service;/*** author hrui* date 2023/9/25 8:42*/ public class OrderServiceImpl implem…...

代码随想录二刷 Day23
669. 修剪二叉搜索树 找到小数字的右子树与大数字左子树必须要重新检查一遍然后让root的左右直接指向return的左右节点; class Solution { public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root NULL) return NULL;if (root->val < low…...

Ubuntu `apt` 报错 “Errors were encountered while processing: base-passwd“ 的解决方法
Ubuntu apt 更新时出现报错: Setting up base-passwd (3.5.52build1) ... Changing home-directory of irc from /var/run/ircd to /run/ircd 1 changes have been made, rewriting files Writing passwd-file to /etc/passwd Error making backupfile /etc/passwd…...
XXL-JOB分布式任务调度
XXL-JOB分布式任务调度 在实际项目中,为了降低耦合,通常会把定时任务的逻辑单独抽离出来,构建成一个新的工程。也有可能需要定时任务实现高可用,组建成集群,提高容错率。 那么问题也就来了。既然定时任务是多个…...

加拿大人工智能数据搜索平台【Secoda】完成1400万美元A轮融资
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于加拿大多伦多的人工智能数据搜索平台【Secoda】今日宣布已完成1400万美元A轮融资。 本轮融资由Craft Ventures领投,参与投资的投资机构有Abstract Ventures、现有投资者YCombi…...

less与sass
1.变量: Less: my-color: #ff0000;.container {background-color: my-color; } Sass:$my-color: #ff0000;.container {background-color: $my-color; } 在这点上,Less和Sass的变量概念基本相同,都是以声明的方式存储值,然后在…...

已解决: Go Error: no Go files in /path/to/directory问题
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页: 🐅🐾猫头虎的博客🎐《面试题大全专栏》 🦕 文章图文并茂🦖…...

2022年6月和7月的工作经历
6月 3D打标软件 3D打标软件,要求在Open3d上加几个2D文字。大致有如下几个方案: 依葫芦画瓢,但O3DVisualizer派生于gui::Window,我的程序派生于Visualizer。工作量不小。 利用OpenGL输出文字,Baidu的两种方法一个编…...

【图像处理】SIFT角点特征提取原理
一、说明 提起在OpenCV中的特征点提取,可以列出Harris,可以使用SIFT算法或SURF算法来检测图像中的角特征点。本篇围绕sift的特征点提取,只是管中窥豹,而更多的特征点算法有: Harris & Stephens / Shi–Tomasi 角点…...

flutter开发实战-应用更新apk下载、安装apk、启动应用实现
flutter开发实战-应用更新apk下载、安装apk、启动应用实现 在开发过程中,经常遇到需要更新下载新版本的apk文件,之后进行应用更新apk下载、安装apk、启动应用。我们在flutter工程中实现下载apk,判断当前版本与需要更新安装的版本进行比对判断…...

DispatcherServlet初始化之Spring容器创建1.0
一、前言 在SpringMVC框架中,DispatcherServlet扮演着非常重要的角色,它负责接收所有的HTTP请求并将其分发给相应的处理器。在DispatcherServlet的初始化过程中,会创建一个Spring容器来管理应用程序中的Bean。 二、步骤 1、加载配置文件&a…...

CSS的基础
CSS美化HTML,布局网页 CSS最大的价值:由HTML专注去做结构呈现,样式给CSS,结构(HTML)与样式(CSS)相分离 CSS主要由选择器以及一条或多条声明 在<head></head>中实现CSS在<body…...

mathtype如何嵌入到word中?详细mathtype安装步骤教程
mathtype是一款功能特别强大的数学方式编辑软件,为用户提供各种强大的数学公式符号帮助用户进行计算,并且速度很快。有小伙伴知道mathtype如何嵌入到word中吗,这里小编就给大家详细介绍一下mathtype嵌入到word中的方法,有需要的小…...
云安全之访问控制的常见攻击及防御
访问控制攻击概述 访问控制漏洞即应用程序允许攻击者执行或者访问某种攻击者不具备相应权限的功能或资源。 常见的访问控制可以分为垂直访问控制、水平访问控制及多阶段访问控制 (上下文相关访问控制),与其相应的访问控制漏洞为也垂直越权漏洞(普通用户可以访问或…...
Java编程技巧:跨域
目录 1、跨域概念2、后端CORS(跨域资源共享)配置原理3、既然请求跨域了,那么请求到底发出去没有?4、通过后端CORS(跨域资源共享)配置解决跨域问题代码4.1、SpringBoot(FilterRegistrationBean&a…...
react create-react-app 配置less
环境信息: create-react-app:v5 react:18.2.0 node:18.16.0 如果你不必须使用 less 建议直接使用scss。 因为less配置会遇到很多问题。 配置less过程: 如果你只需要 sass的话,就可以直接使用sass。因为默认配置了scss。 npm、yarn、cnpm、…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...