数据结构与算法基础(青岛大学-王卓)(8)
哎呀呀,sorry艾瑞波地,这次真的断更一个月了,又发生了很多很多事情,秋风开始瑟瑟了,老父亲身体查出肿瘤了,有病请及时就医,愿每一个人都有一个健康的身体,God bless U and FAMILY.
直接上货了 😃
文章目录
- 查找
- 概念
- 线性表的查找
- 顺序查找(线性)
- 应用范围:
- 表示方法:
- 算法:
- 算法7.2时间效率分析:
- 讨论
- 优缺点:
- 折半查找(对半/二分)
- 算法思路
- 二分查找效率分析 - 判定树
- 平均查找长度ASL(成功时)
- 优缺点
- 分块查找(索引顺序查找)
- 条件
- 性能分析
- 优缺点
- 树表的查找
- 二叉排序树 (Binary Sort Tree)
- 二叉排序树定义
- 二叉排序树的性质
- 二叉排序树查找
- 二叉排序树的插入
- 二叉排序树的生成
- 二叉排序树的删除
- 平衡二叉树
- 散列表的查找
- 散列表术语
- 散列函数构造方法
- 直接定址法
- 除留余数法
- 处理冲突的方法
- 开放地址法
- 链地址法
- 散列表查找
查找
内容回顾:
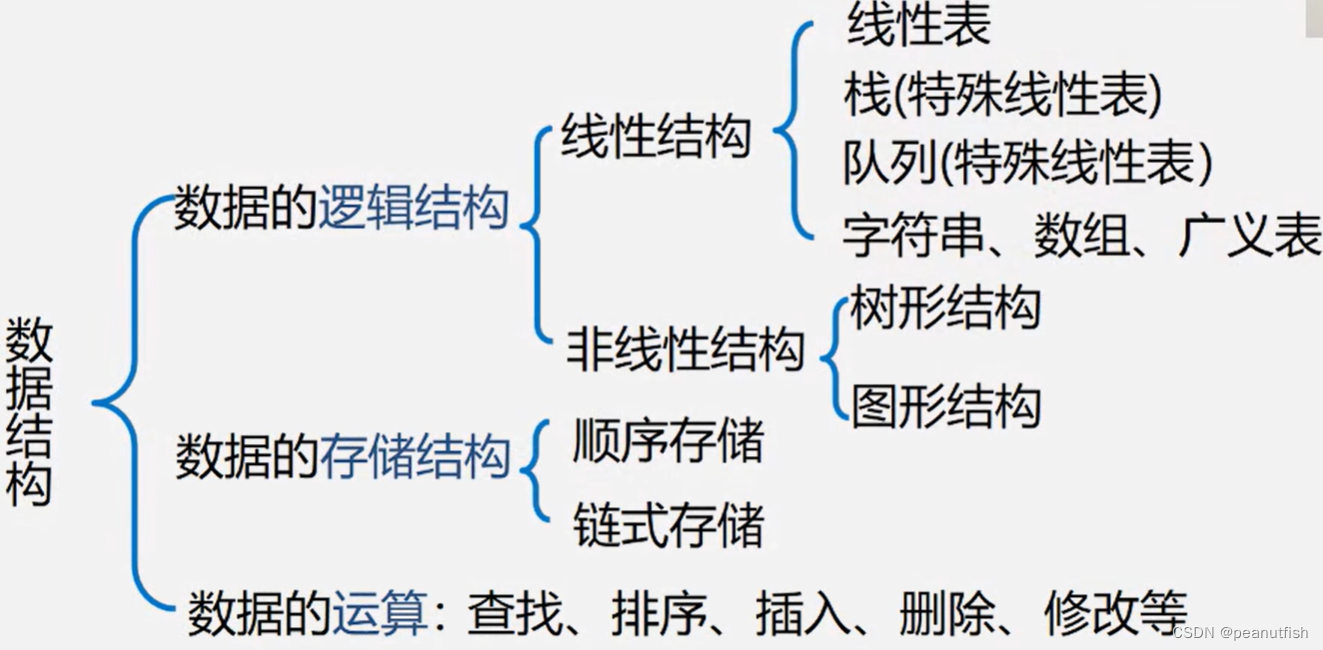
概念
-
查找表是由同一类型的数据元素(或记录)构成的集合。由于"集合"中的数据元素之间存在着松散的关系,因此查找表是一种应用灵便的结构。
-
查找 – 根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素或(记录),查找成功返回该记录信息或者位置,查找不成功则给出空记录或者空指针。
-
关键字:用来标识一个数据元素(或记录)的某个数据项的值。分为 主关键字(可唯一地标识一个记录的关键字) 和 次关键字(用以识别若干记录的关腱字)。
-
对查找表的操作:查询记录, 检索属性, 插入数据元素, 删除数据元素。
-
查找表分类:
- 静态(仅查询)
- 动态(可插入,删除)
-
查找算法的评价指标 – 平均查找长度(关键字的平均比较次数) – ASL(Average Search Length)

-
查找的方法取决于查找表的结构,即表中数据元素是依何种关系组织在一起的。为提高查找效率,一个办法就是在构造查找表时,在集合中的数据元素之间人为地加上某种确定的约束关系。
线性表的查找
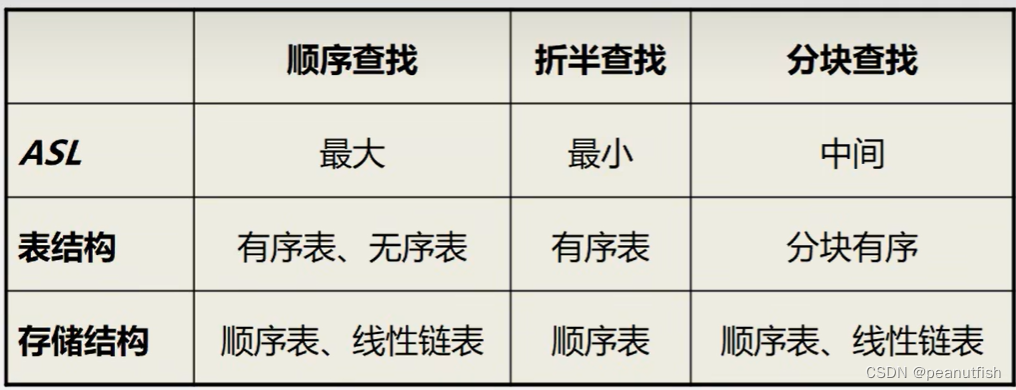
顺序查找(线性)
应用范围:
- 顺序表或线性链表表示的静态查找表
- 表内元素之间无序
表示方法:
// 数据元素的类型定义
typedef struct {KeyType key; //关键字域...... //其他域
} ElemType;// 顺序表结构类型定义
typedef struct {ElemType *R; // 表基址int length; //表长
} SSTable; //Sequential Search Table//定义一个顺序表ST
SSTable ST;
算法:

// 算法7.1
int Search_Seq(SSTable ST, KeyType key) {// 如成功则返回位置信息,不成功返回0for(i=ST.length; i>=1; --i) {if (ST.R[i].key == key) return i;return 0;}
}
// 算法改1
int Search_Seq(SStable ST, KeyType key) {for(i=ST.length; ST.R[i].key != key; --i)if (i<=0) break;if (i>0) return i;else return 0;
}// 算法改2
inti Search_Seq(SStabl ST, KeyType key) {for(i=ST.length; ST.R[i].key != key&&i>0; --i);if (i>0) return i;else return 0;
}
上面的算法的每一次循序都需要进行两次比较,能否改进?
- 查找的值是否相等
- i的值是否越界
改进:
把待查关键字 key 存入表头("哨兵、“监视哨”) 从后往前个比较,可免去查找过程中每一步都要检测是否查找完毕,加快速度。(如果找不到在表头[0]位置也一定会找到)。
当ST.length较大时,此改进能使进行一次查找所需的平均时间几乎减少一半。
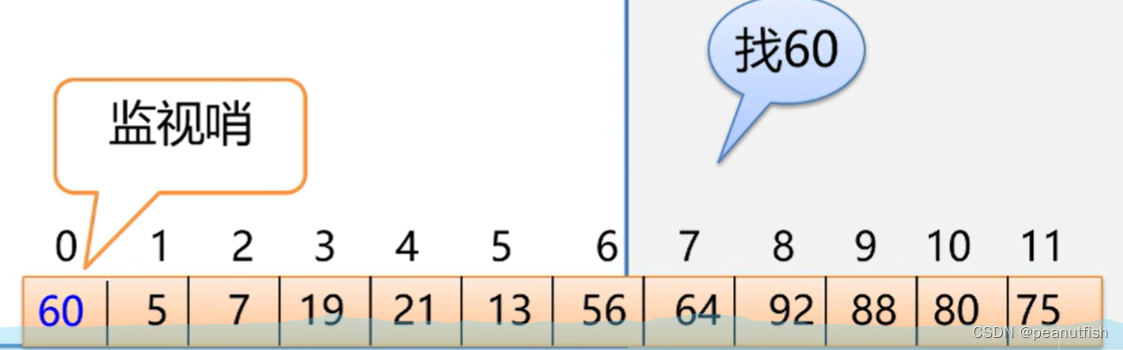
// 改进算法7.2
int Search_Seq(SSTable ST, KeyType key) {ST.R[0].key = key;for (i=ST.length; ST.R[i].key != key; --i);return i;}
}
算法7.2时间效率分析:

时间复杂度:O(n)
查找成功时的平均查找长度,设表中各记录查找概率相等(注意这里是指的是查找成功时所以不算哨兵位置)
ASLs(n)=(1 + 2 +…+ n)/n = (n+1)/2
空间复杂度:O(1) — 辅助空间用于哨兵位置
讨论
1 、记录的查找概率不相等时如何提高查找效率?
查找表存储记录原则按照查找概率高低存储:1 )查找概率越高,比较次数越少;2 )查找概率越低,比较次数较多。
2 、记录的查找概率无法测定日日何提高查找效率?
方法 – 按查找概率动态调整记录顺序.1 )在每个记录中设一个访问频度域;2 )始终保持记录按非递增有序的次序排列;3 )每次查找后均将刚查到的记录直接移至表头。
优缺点:
优点:算法简单,逻辑次序无要求,且不同存储结构均适用。
缺点:ASL 太长,时间效率太低。
折半查找(对半/二分)
折半查找:每次将待查记录所在区间缩小一半。
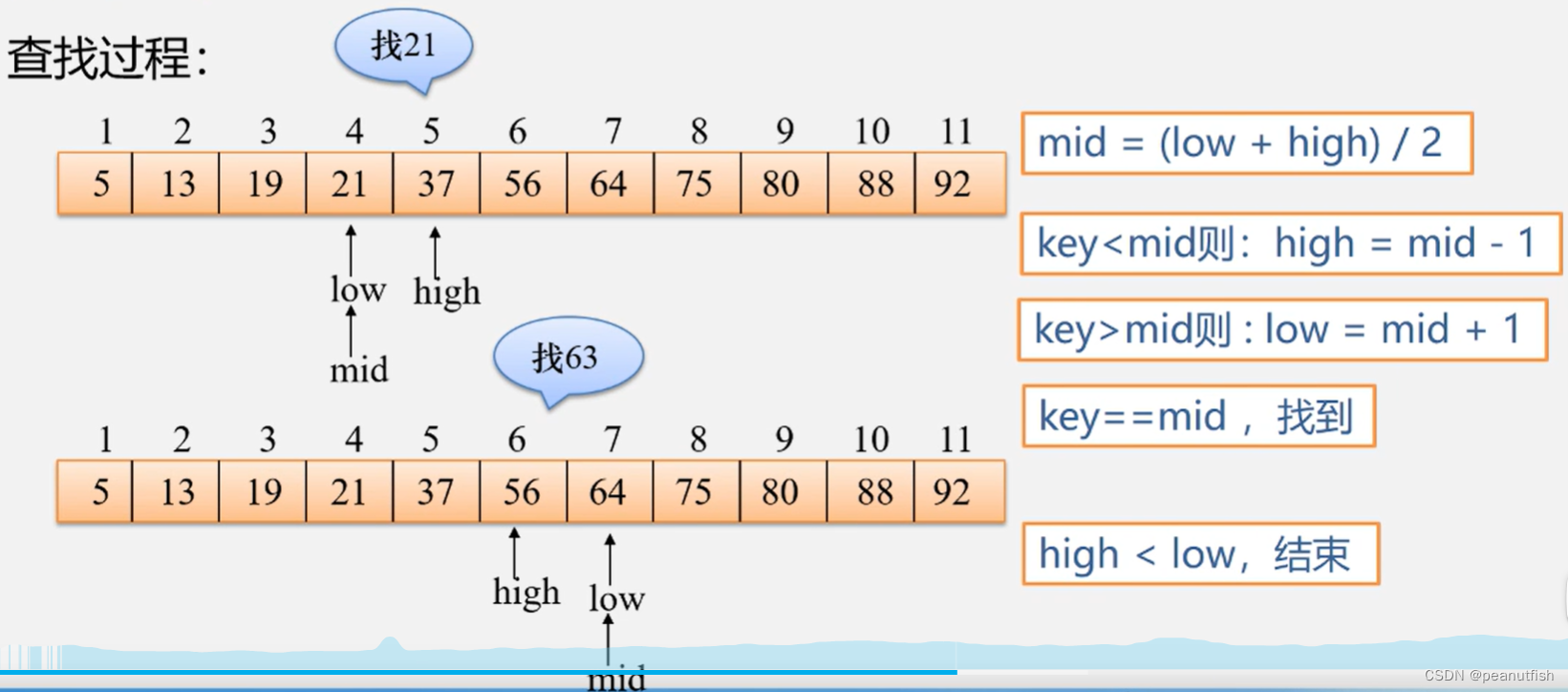
算法思路
非递归算法
-
设表长为n,low、high 和 mid 分别指向待查元素所在区间的上界、下界和中点, key 为给定的要查找的值.
-
初始时,令low = 1,high=n, mid=$\lfloor(low+high)/2\rfloor $
-
让 k 与 mid 指向的记录比较
- 若key == R[mid].key 查找成功
- 若key < R[mid].key, 则 high=mid-1
- 若 key > R[mid].key, 则 low=mid+1
-
重复上述操作,直至 low>high 时,查找失败
// 二分查找(非递归)
int Search_Bin(SSTabl ST, KeyType key) {low = 1;high = ST.length; // 初始化置区间值while (low <= high) { mid = (low + high) / 2;if (ST.R[mid].key == key) return mid; // 找到元素else if (ST.R[mid].key < key) { // 缩小区间low = mid + 1; // 继续在后半区查找} else high = mid -1; // 继续在前半区查找}return 0; // 表中不存在待查元素
} // Search_Bin// 二分查找(递归)
int Search_Bin(SSTable ST, KeyType key, int low, int high) {if (low > high) return 0; // 查找不到时返回0mid = (low + high)/2if (ST.R[mid].key == key) return mid;else if (ST.R[mid].key > key) {Search_Bin(ST, key, low, mid-1);} else {Search_Bin(ST, key, mid+1, high);}
}
二分查找效率分析 - 判定树
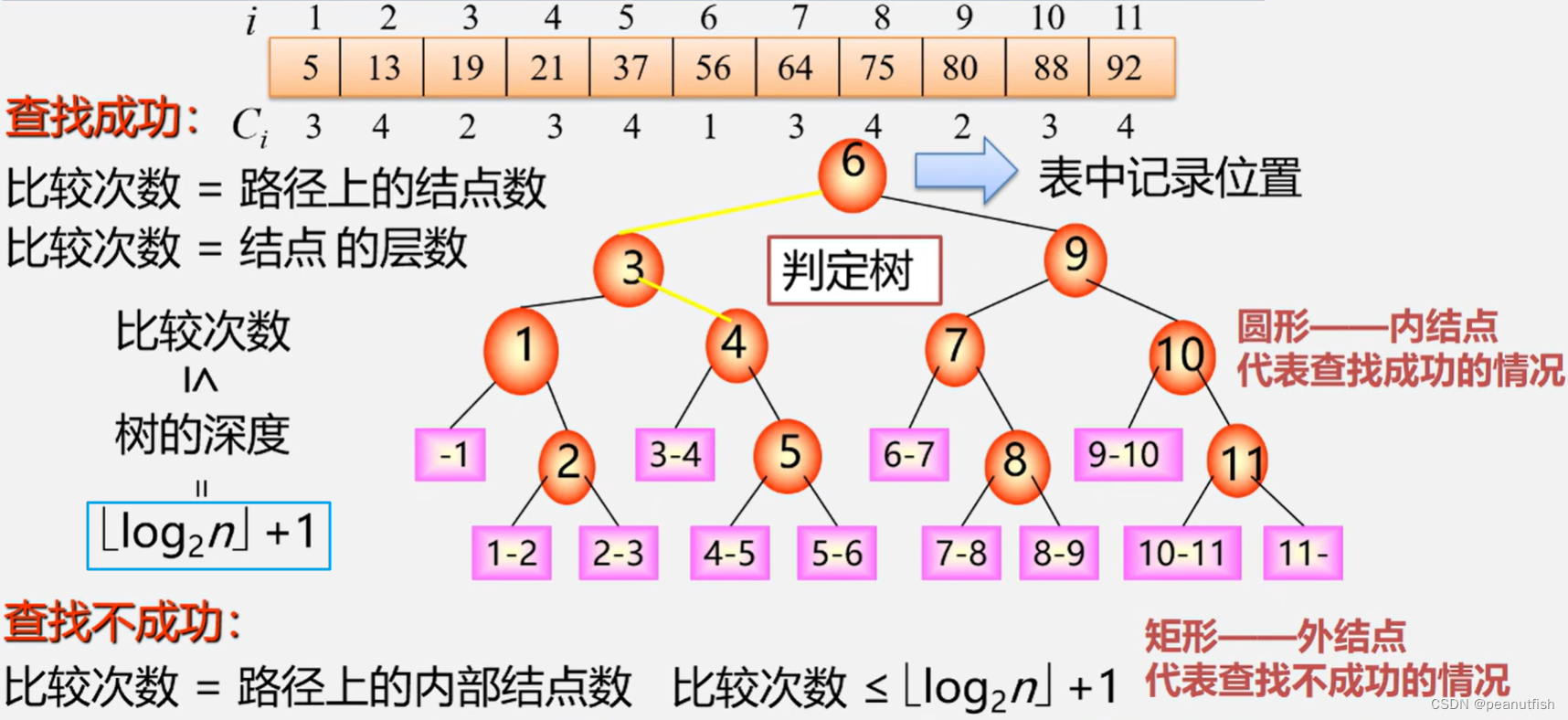
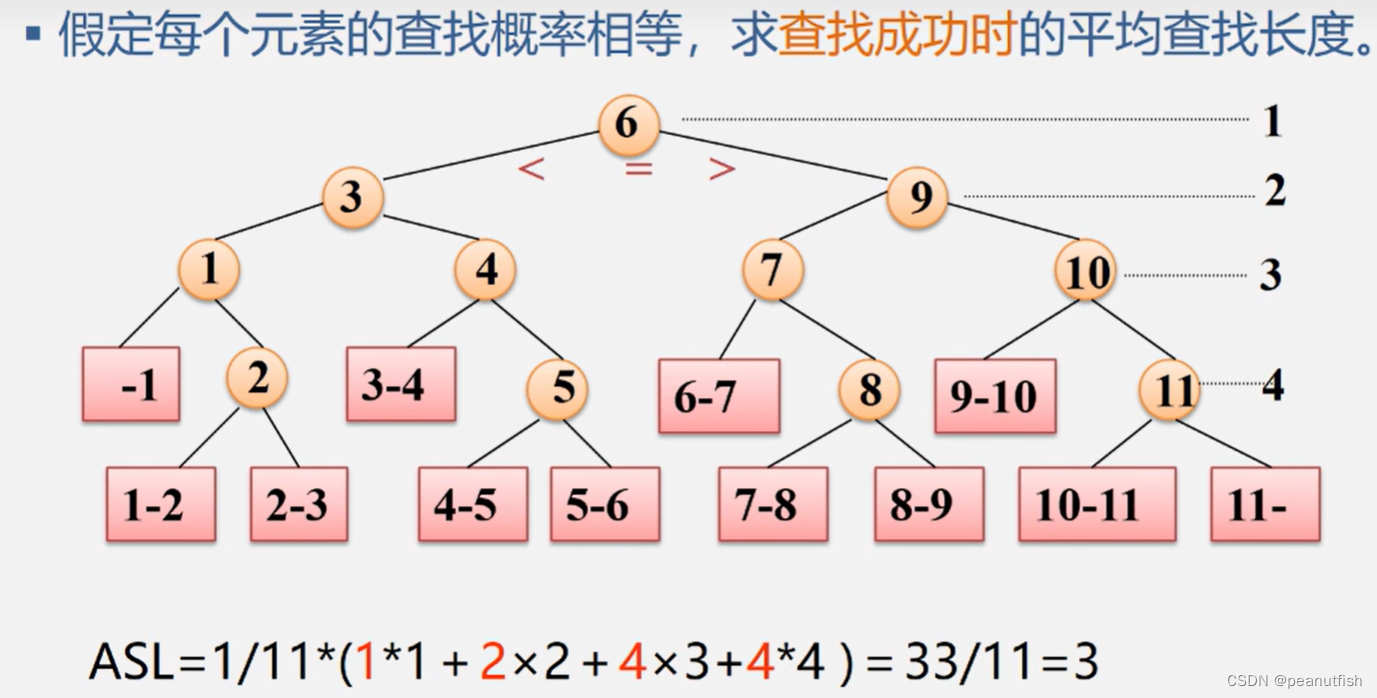
平均查找长度ASL(成功时)

优缺点
折半查找优点:效率比顺序查找高
折半查找缺点:只适用于有序表,且限于顺序存储结构(对线性链表无效)。
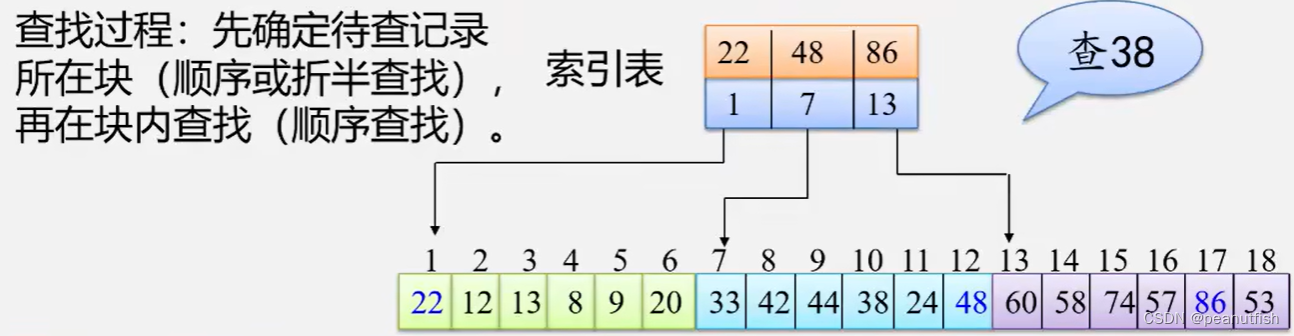
分块查找(索引顺序查找)
条件
-
将表分成几块,且表或者有序,或者分块有序;若i < j,则第 j 块中所有记录的关键字均大于第 i 块中的最大关键字。
-
建立"索引表"(每个结点含有最大关键字域和指向本块第一个结点的指针,且按关键字有序)。
查找过程:找38 --> 目标在索引48的块中 --> 顺序/折半在块内查找–> 找到38
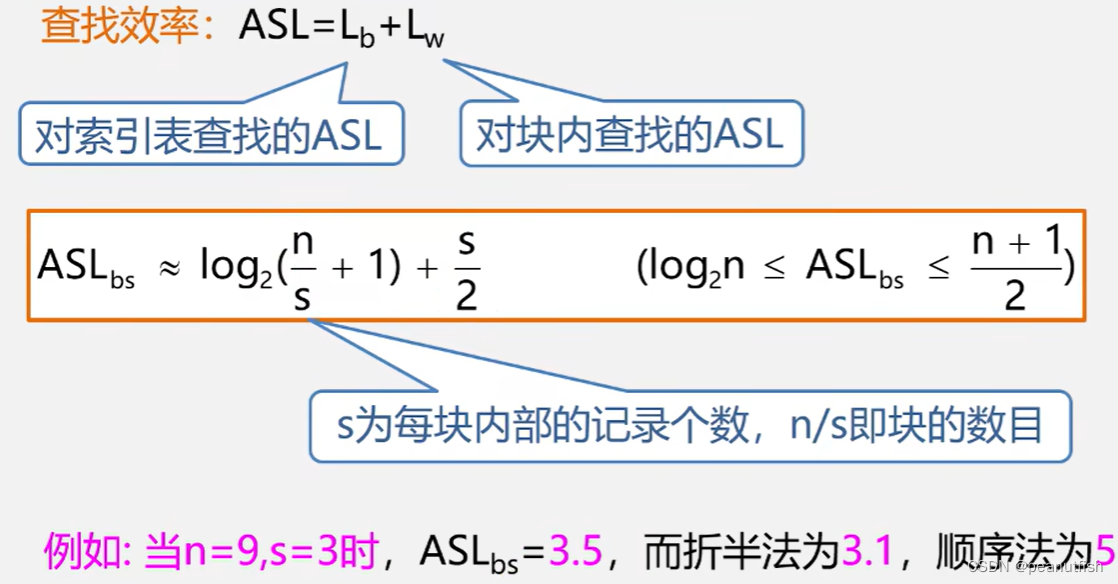
性能分析
优缺点
优点:插入和删除比较容易,无需进行大量移动。
缺点:要增加一个索引表的存储空间并对初始索引表进行排序运算。
适用情况如果线性表既要快速查找又经常动态变化,则可采用分块查找。
树表的查找
动态查找表 – 几种特殊的树, 用来解决插入,删除频繁操作但需要维护表的有序性情况。
表结构在查找过程中动态生成对于给定值 key若表中存在,则成功返回;否则,插入关字等于 key 的记录
分类:
- 二叉排序树
- 平衡二叉树
- 红黑树
- B- 树
- B+ 树
- 键树
二叉排序树 (Binary Sort Tree)
又称为二叉搜索树、二叉查找树
二叉排序树定义
二叉排序树或是空树,或是满足如下性质的二叉树:
-
若其左子树非空,则左子树上所有结点的值均小于根结点的值;
-
若其右子树非空,则右子树上所有结点的值均大于等于根结点的值;
-
其左右子树本身又各是一棵二叉排序树
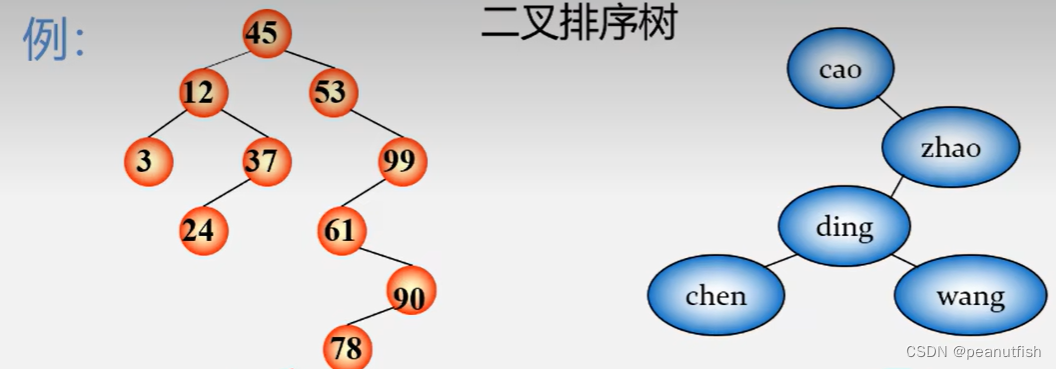
二叉排序树的性质
中序遍历非空的二叉排序树所得到的数据元素序列是一个按关键字排列的递增有序序列。
如上图就是 3 12 24 37 45 53 61 78 90 100
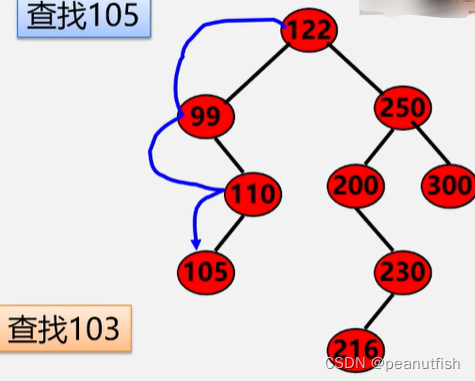
二叉排序树查找
算法
typedef struct {KeyType key; //关键字项infoType otherinfo; //其他数据域
}ElemType;typedef stuct BSTNode {ElemType data; //数据域struct BSTNode *lchild, *rchild; //左右孩子指针
}BSTNode, *BSTree;BSTree T; //定义二叉排序树T

BSTree SearchBST(BSTree T, KeyType key) {if (!T) || (key == T->data.key) return T; //表为空或者表不为空且找到了都返回一个指针T(BSTree类型)else if (key < T->data.key) // 判断key在左右子树的位置return SearchBST(T->lchild, key); //继续在左子树上找else return SearchBST(T->rchild, key); //继续在右子树上找
}//SearchBST
平均查找长度
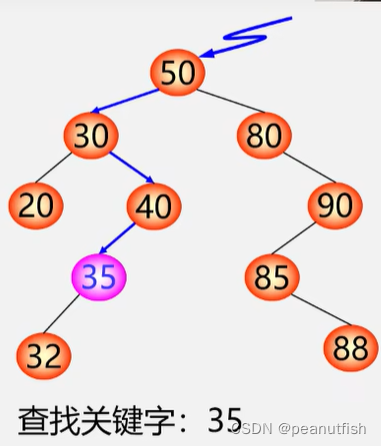
二叉排序树上查找某关键字等于给定值的结点过程,其实就是走了一条从根到该结点的路径。

总结:含有 n 个结点的二叉排序树的平均查找长度和树的形态有关

二叉排序树的插入
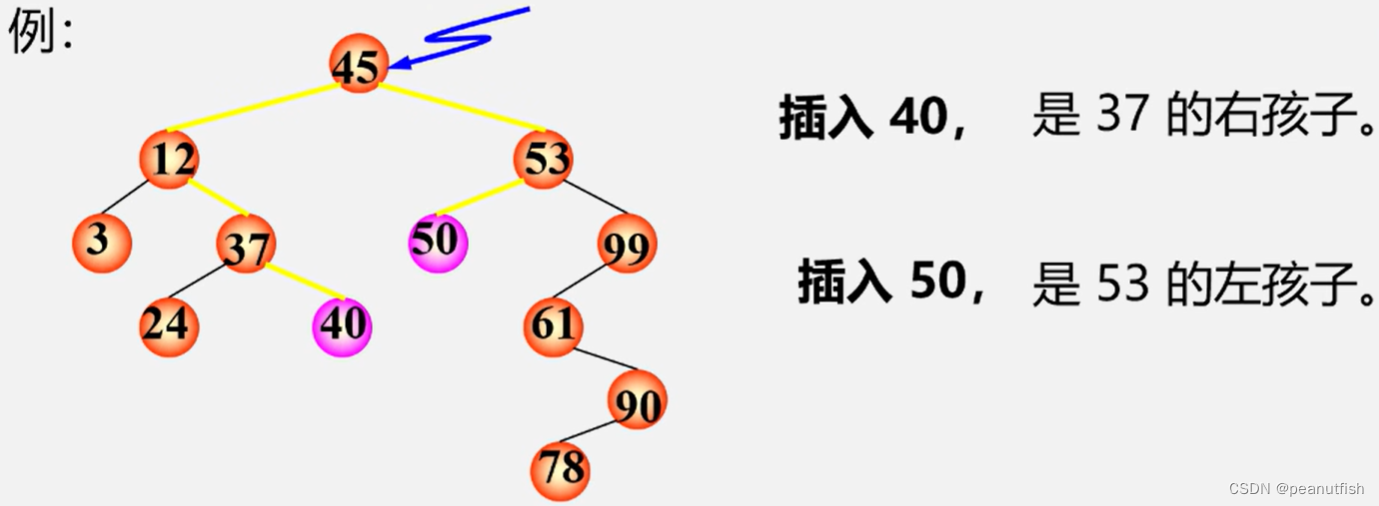
-
若二叉排序树为空,则插入结点作为根结点插入到空树中
-
否则,继续在其左、右子树上查找
-
树中已有,不再插入
-
树中没有
- 查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应为该叶子结点的左孩子或右孩子
-
-
插入的元素一定在叶结点
二叉排序树的生成
-
从空树出发,经过一系列的查找、插入操作之后,可生成一棵二叉排序树。
-
一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。(插入的结点均为叶子结点,故无需移动其他结点)
-
关键字的输入顺序不同,建立的不同二叉排序树。
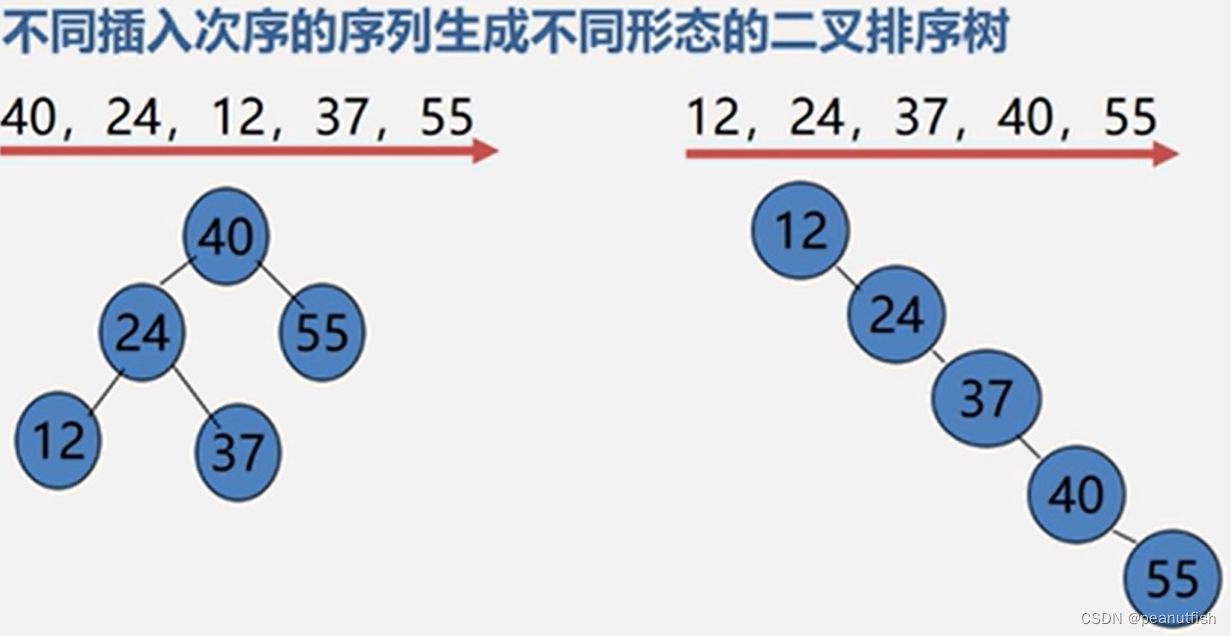
二叉排序树的删除
从二叉排序树中删除一个结点,不能把以该结点为根的子树都删掉,只能删掉该结点,并且还应保证删除后所得的二叉树仍然满足二叉排序树的性质不变。在二叉排序树中删去一个结点相当于删去有序序列中的一个结点。(中序遍历二叉树得到递增有序的序列)
-
被删除的结点是叶子结点:直接删去该结点。
-
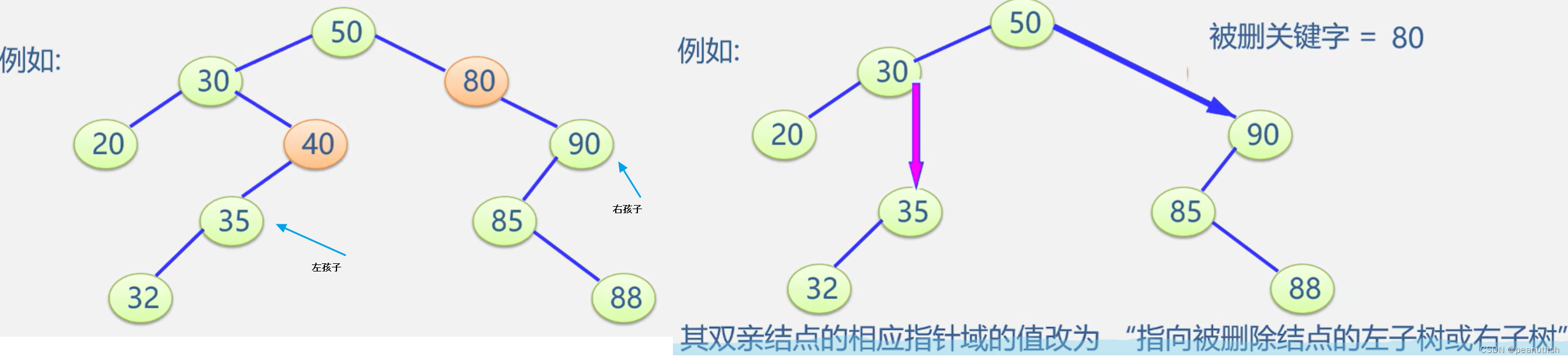
被删除的结点只有左子树或者只有右子树,用其左子树或者右子树替换它(结点替换)。
其双亲结点的相应指针域的值改为“指向被删除结点的左子树或者右子树”
-
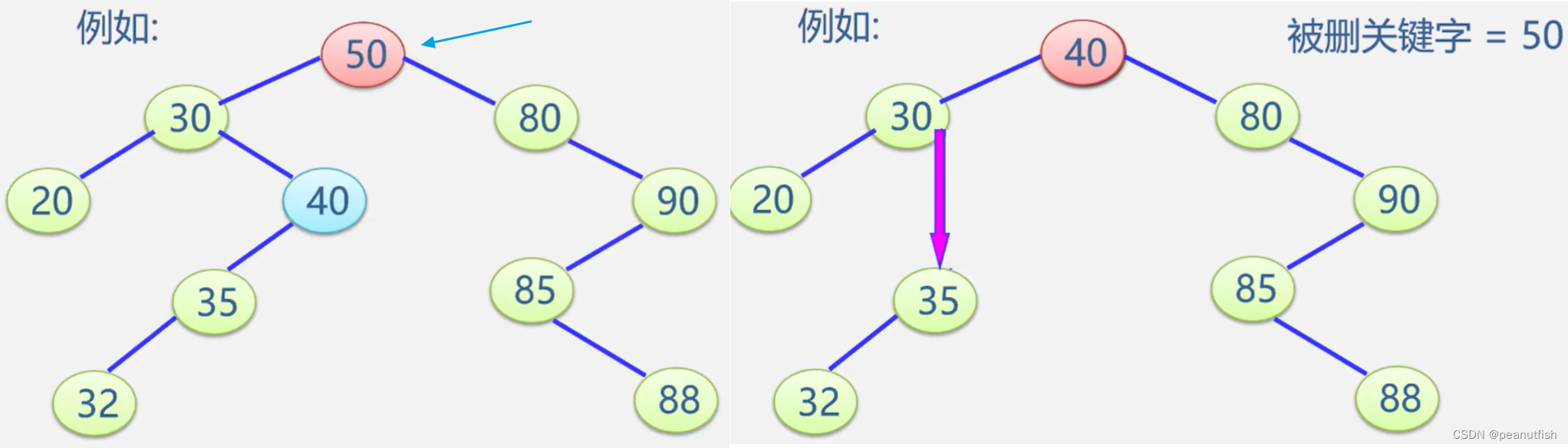
被删除的结点既有左子树,也有右子树
以其中序前趋值替换之(值替换),然后再删除该前趋结点。前趋是左子树中最大的结点。
也可以用其后继替换之,然后再除该后继结点。后继是右子树中最小的结点。
-
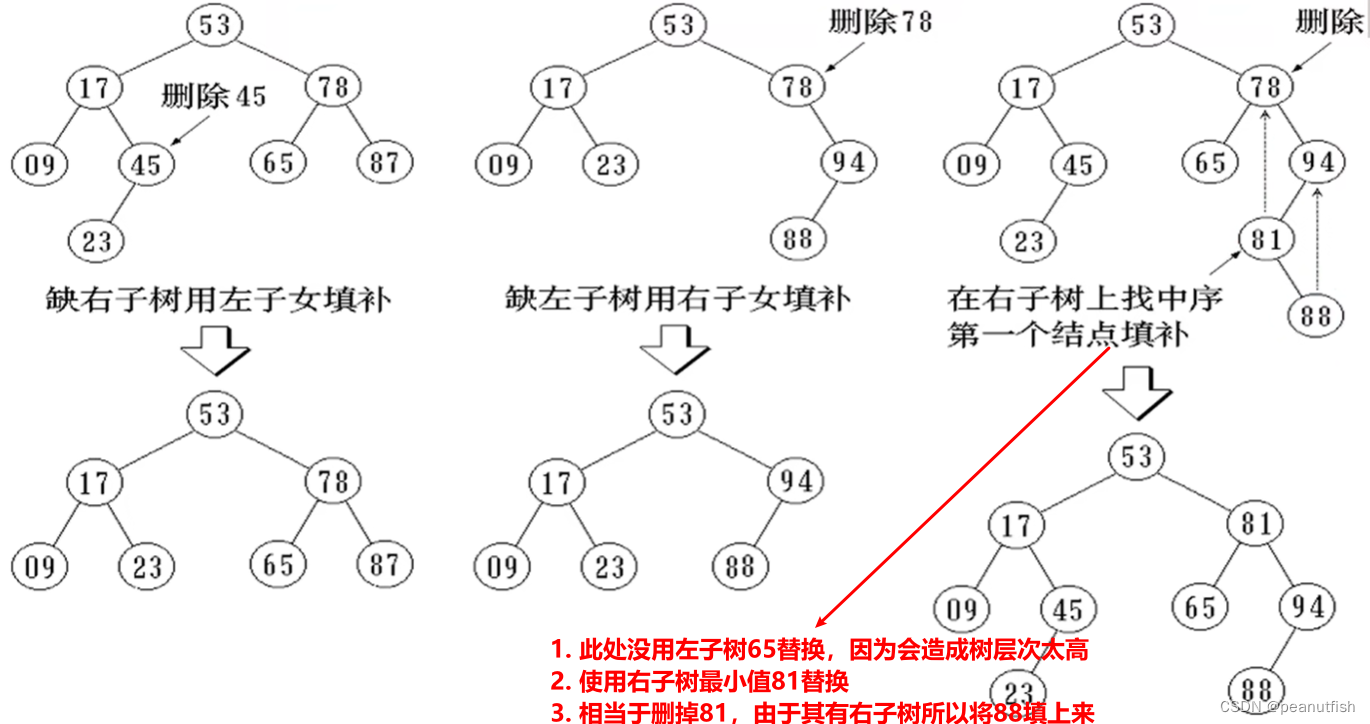
总结图:
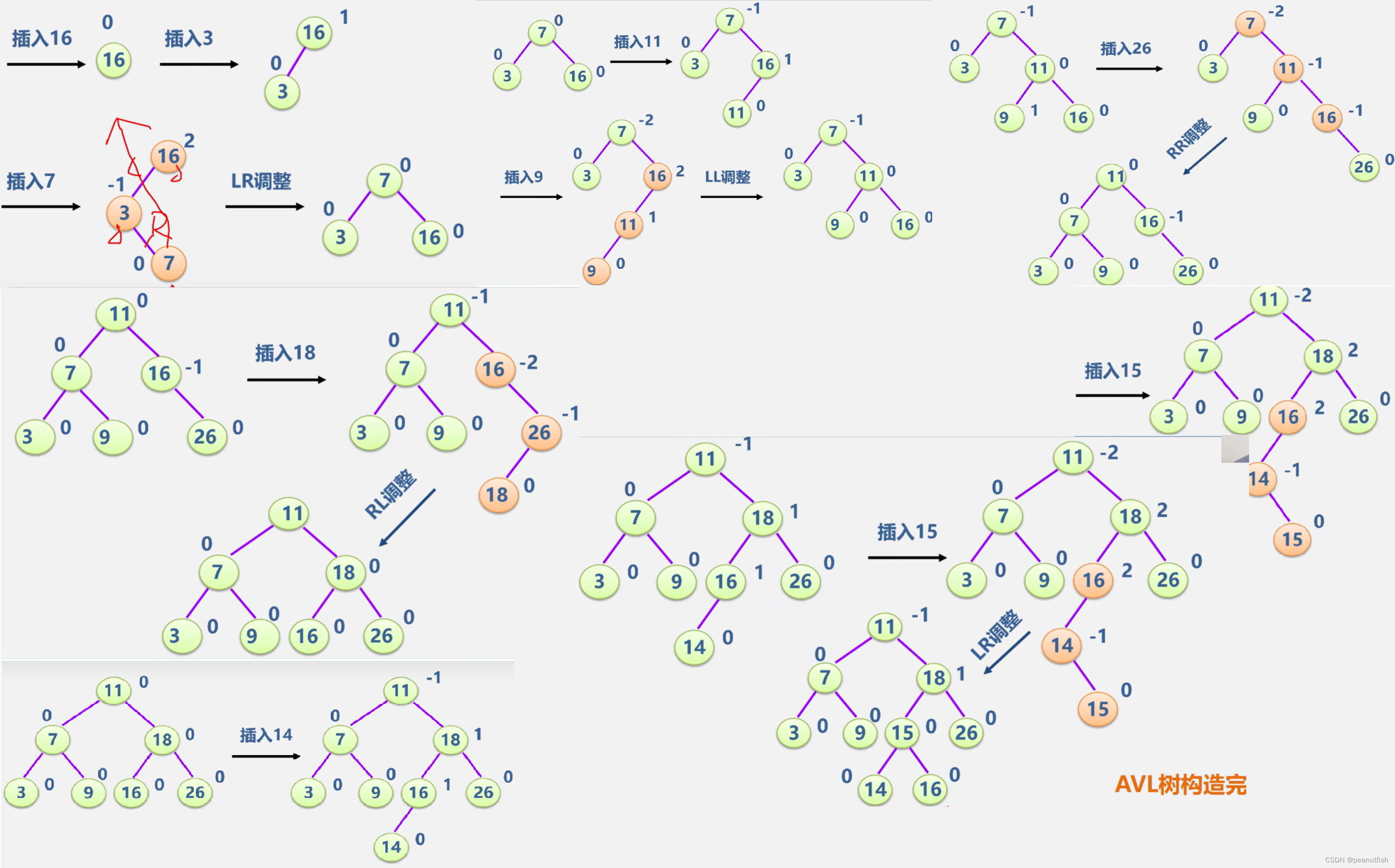
平衡二叉树
平衡二叉树 (balanced binary tree)又称 AVL (Adelson VeIskii and Landis)
一棵平衡二叉树或者是空树,或者是具有下列性质的二叉排序树.
- 左子树与右子树的高度之差的绝对值小于等于 1
- 左子树和右子树也是平衡二叉排序树。
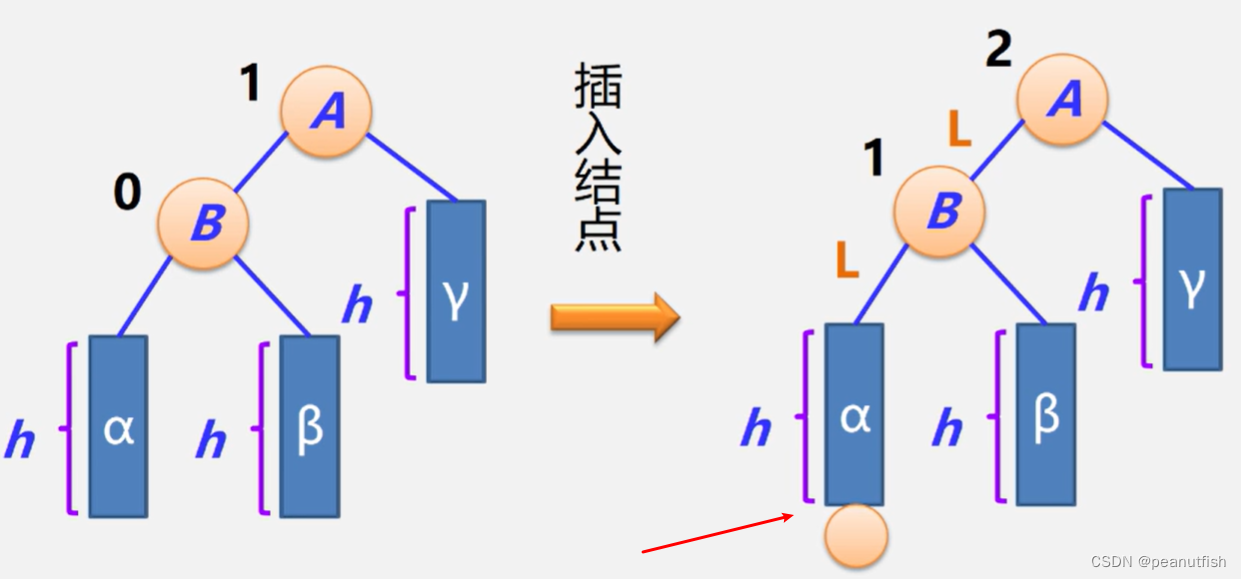
结点的平衡因子 (BF)
-
给每个结点附加一个数字,给出该结点左子树右子树的高度差。值范围(-1, 0 ,1)
-
平衡因子=结点左子树的高度-结点右子树的高度
-
对于一棵有 n 个结点的 AVL 树,其高度保持在 O(log2n )数量级,ASL也保持在 O(log2n )量级
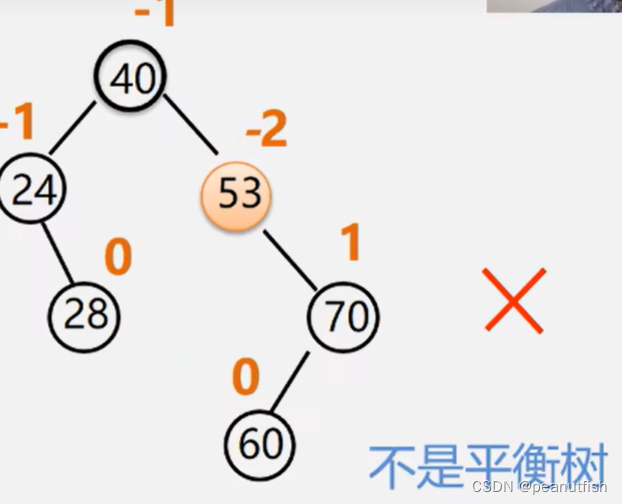
失衡二叉排序树的调整
四种类型
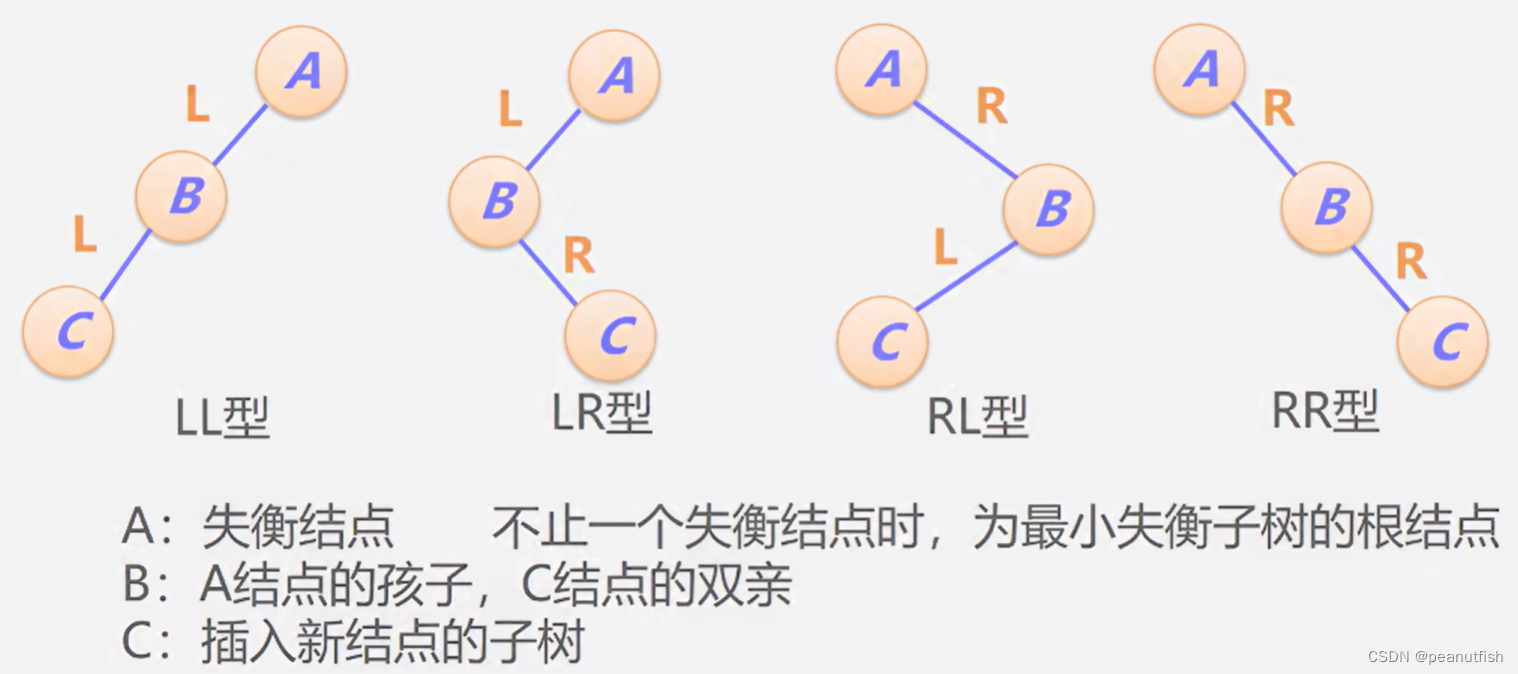
调整原则:
- 降低高度
- 保持二叉排序树的性质
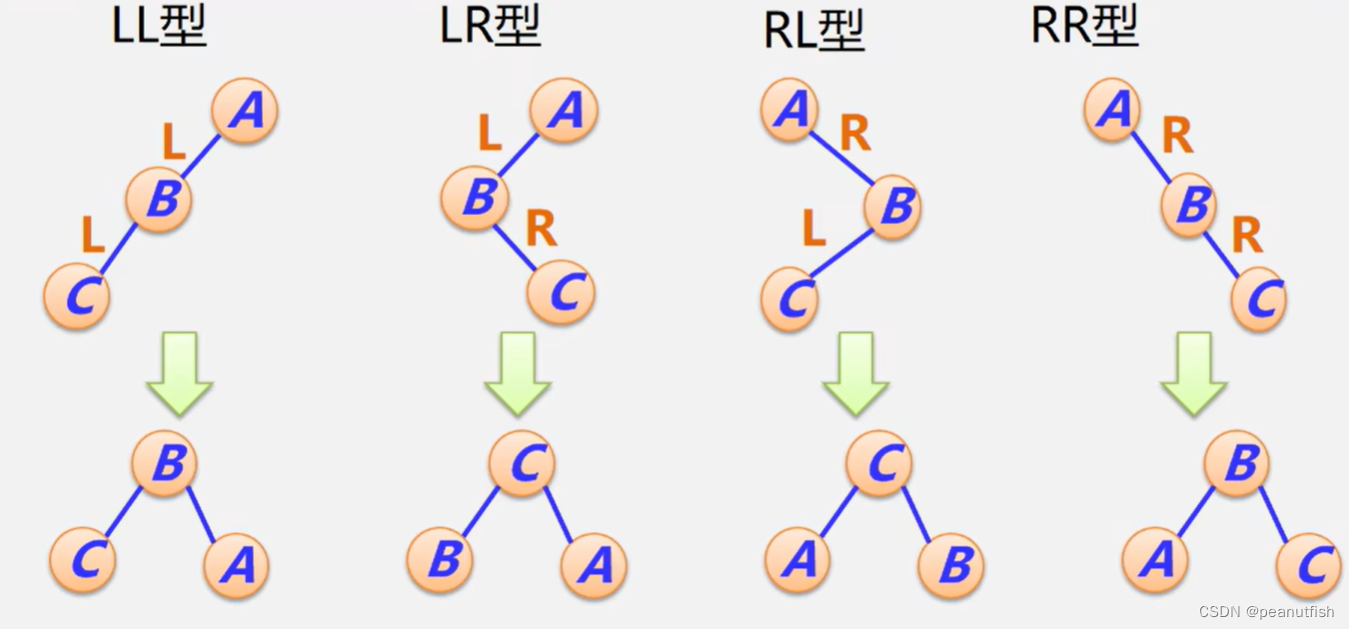
-
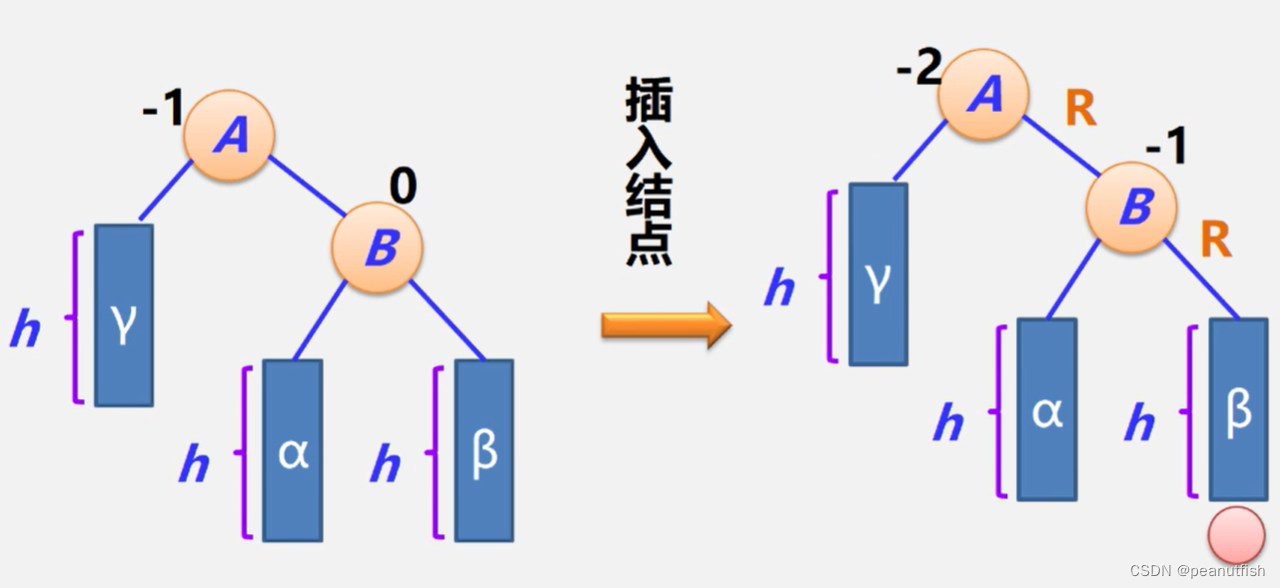
LL型调整

-
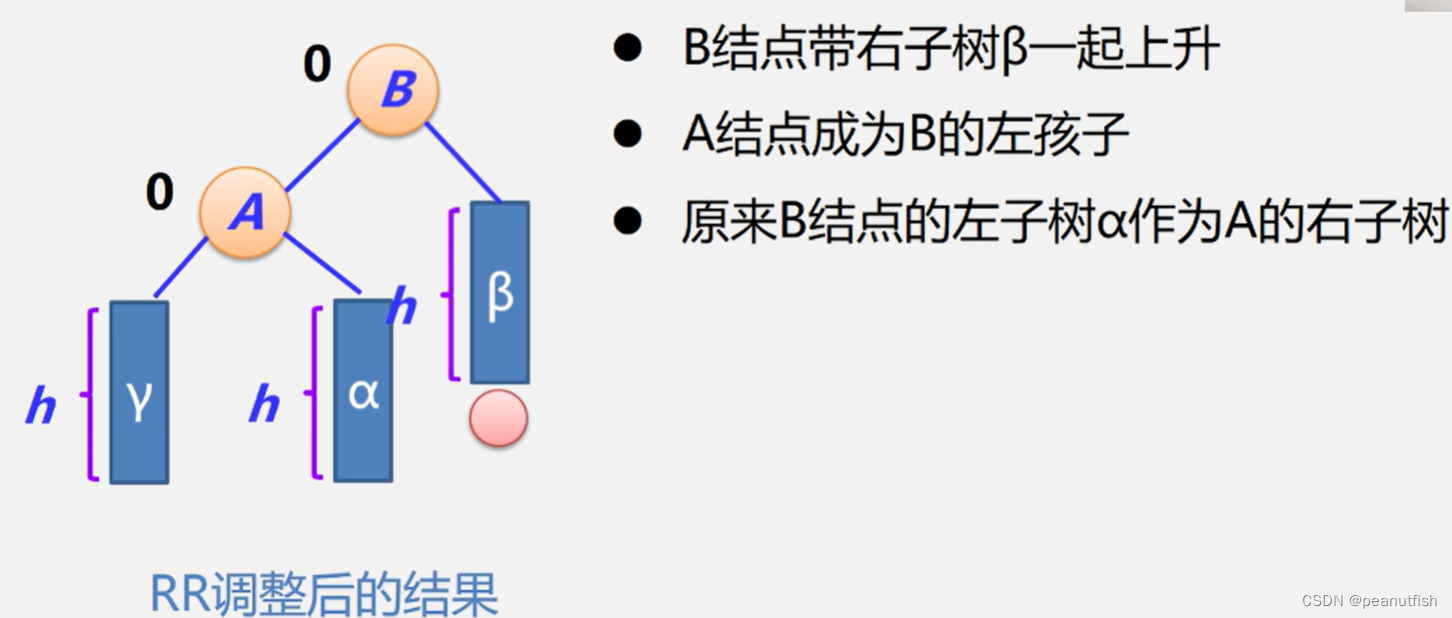
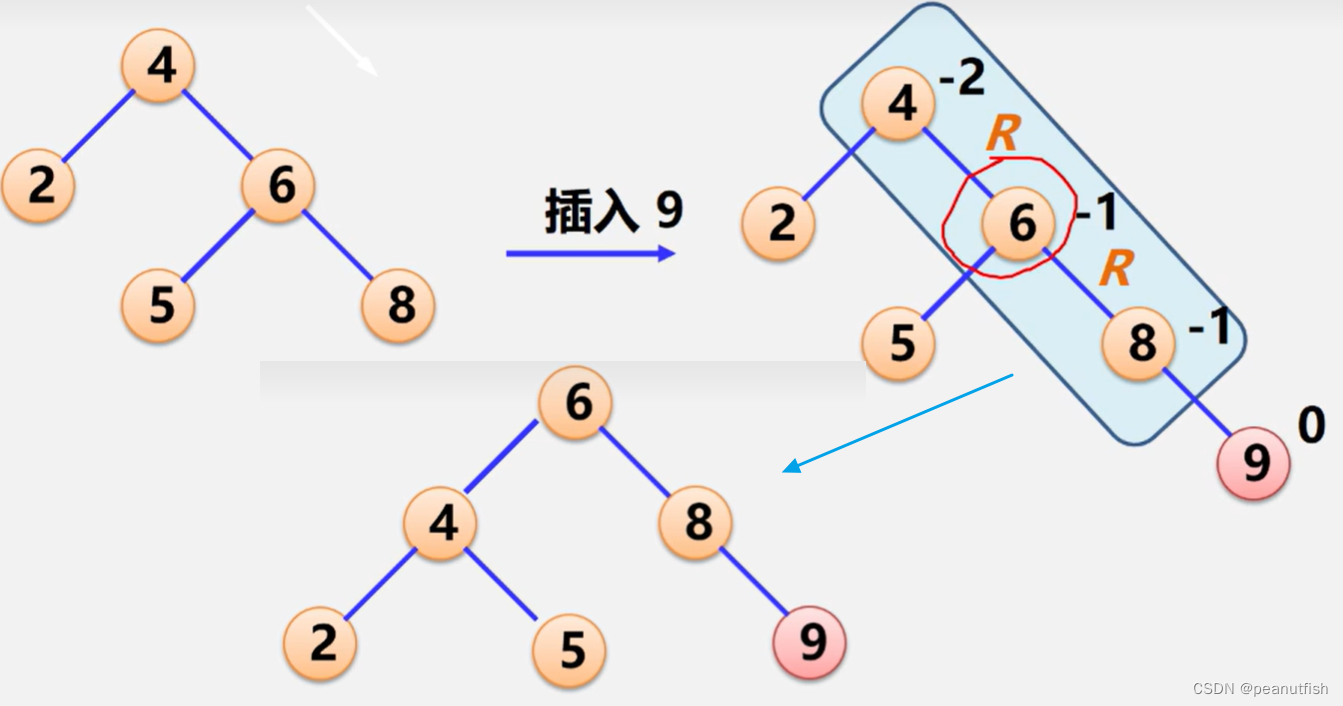
RR型
-
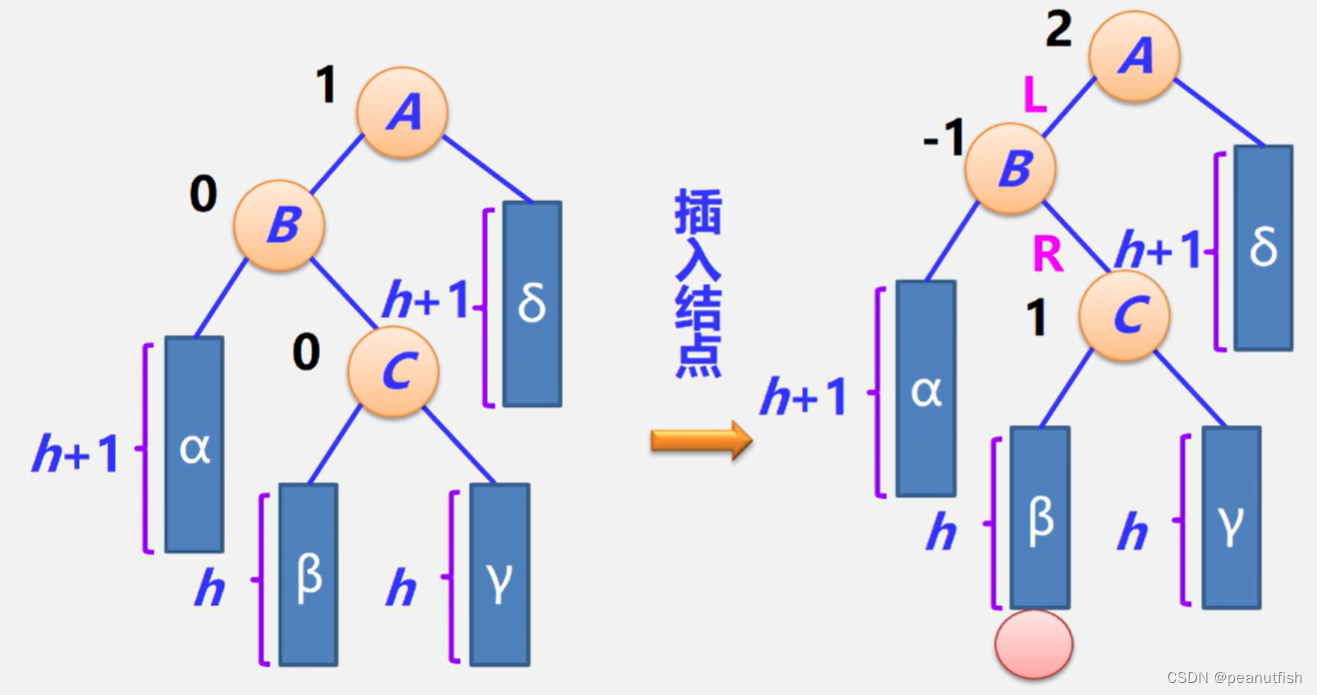
LR型
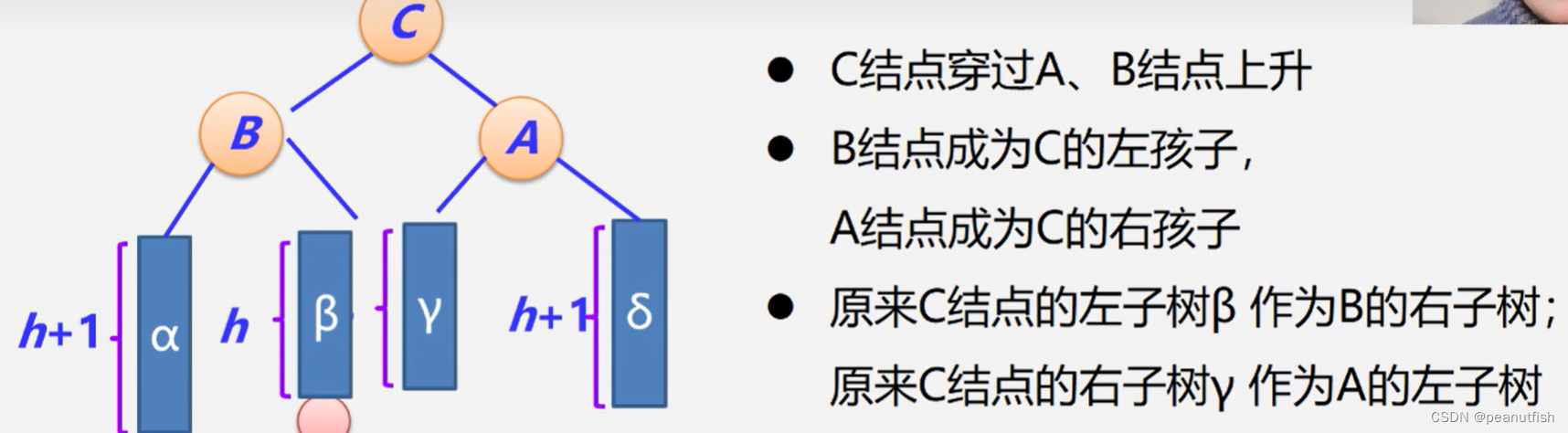
-
RL型
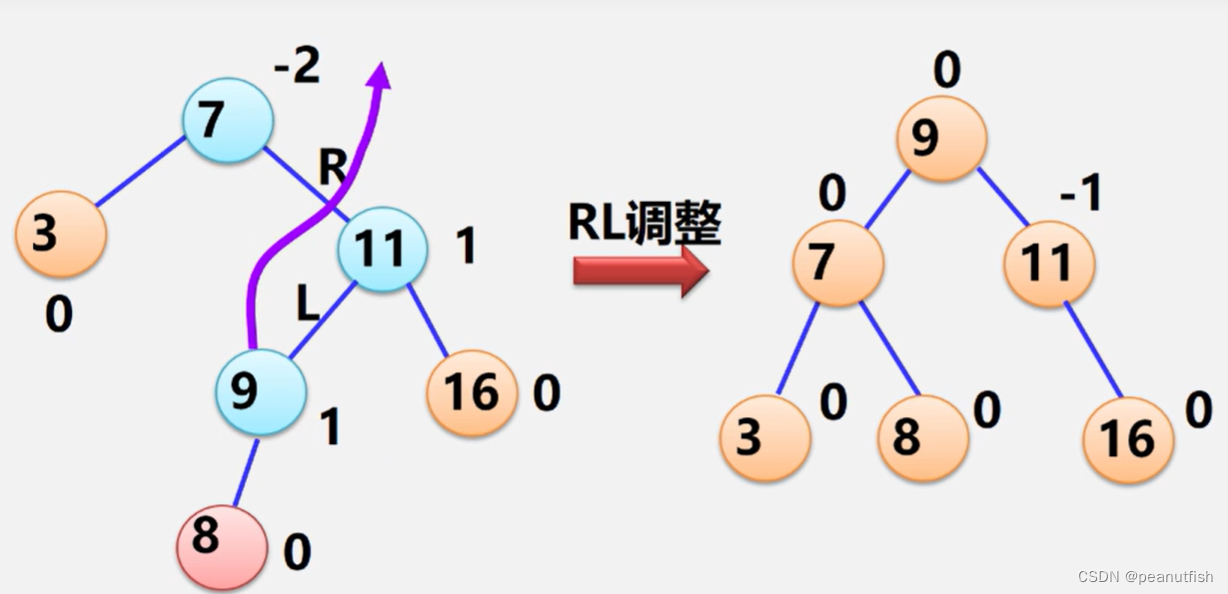
构造案例:
输入关键字序列(16,3,7,11,9,26,18,14,15), 给出构造AVL 树的步骤。
散列表的查找
基本思想:记录的存储位置与关键字之间存在对应关系
对应关系-- hash 函数 Loc(i)= H(keyi)
散列表术语
散列方法(杂凑法):
选取某个函数,依该函数按关键字计算元素的存储位置,并按此存放;查找时,由同一个函数对给定值 k 计算地址,将 k 与地址单元中元素关键码进行比,确定查找是否成功。
散列函数(杂凑函数):散列方法中使用的转换函数
散列表(杂凑表):按上述思想构造的表
散列存储:选取某个函数,依该函数按关键字计算元素的存储位置 Loc(i)=H(keyi)
冲突:不同的关键码映射到同一个散列地址,当key1 != key2 我们的 H(key1)=H(key2)

散列函数构造方法
在散列查找方法中,冲突是不可能避免的,只能尽可能减少。
构造散列函数考虑的因素:
- 执行速度(即计算散列函数所需时间)
- 关键字的长度;
- 散列表的大小;
- 关键字的分布情况;
- 查找频率。
根据元素集合的特性构造
-
要求一:n 个数据原仅占用 n 个地址。虽然散列查找是以空间换时间,但仍希望散列的地址空间尽量小。
-
要求二:无论用什么方法存储,目的都是尽量均匀地存放元素,以避免冲突。
有以下方法:
- 直接定址法
- 数字分析法
- 平方取中法
- 折叠法
- 除留余数法(最常用)
- 随机数法
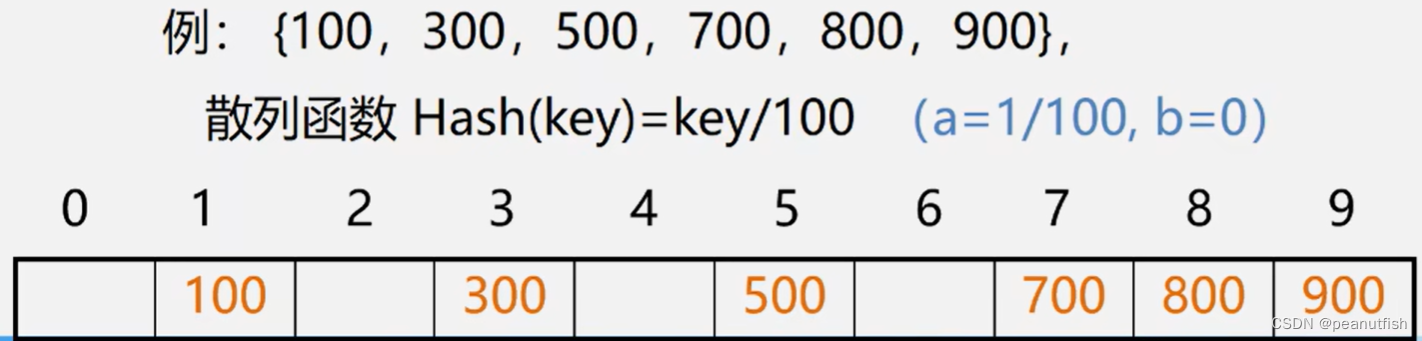
直接定址法
Hash(key) = a*key + b (a 、b为常数)
优点:以关键码 key 的某个线性函数值为散列地址,不会产生冲突。
缺点:要占用连续地址空间,空间效率低。
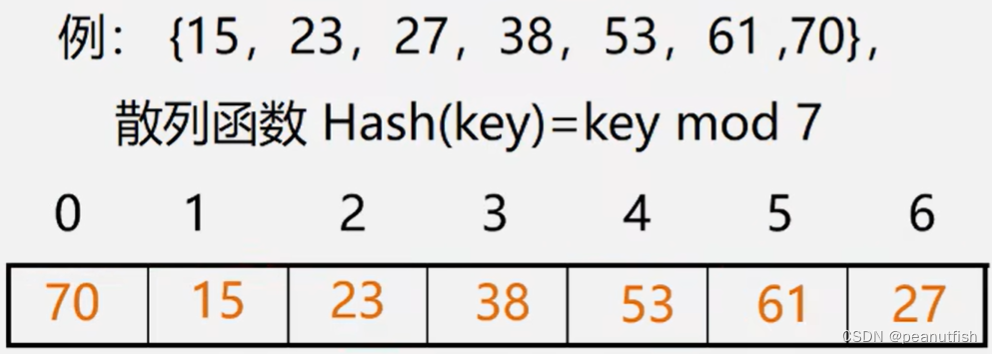
除留余数法
Hash(key)= key mod p( p 是一个整数)
如何取p: 设表长为 m ,取 p <= m 且为质数
处理冲突的方法
方法:
- 开放定址法(开地址法)
- 链地址法(拉链法)
- 再散列法(双散列函数法)
- 建立一个公共溢出区
开放地址法
基本思想:有冲突时就去寻找下空的散列地址,只要散列表足够大,空的散列地址总能找到,并将数据元素存入。
例如:除留余数法Hi=(Hash(key)+di) mod m (di 为增量序列)
常用方法:线性探测法;二次探测法;伪随机法

线性探测法

例:关键码集为{47,7,29,11,16,92,22,8,3}, 散列表长为 m = 11 ;散列函数为 Hash(key)=key mod 11 ;拟用线性探测冲突。建散列表如下:

二次探测法:

伪随机探测法:

链地址法
基本思想:相同散列地址的记录链成一单链表
m个散列地址就设 m个单链表,然后用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构。
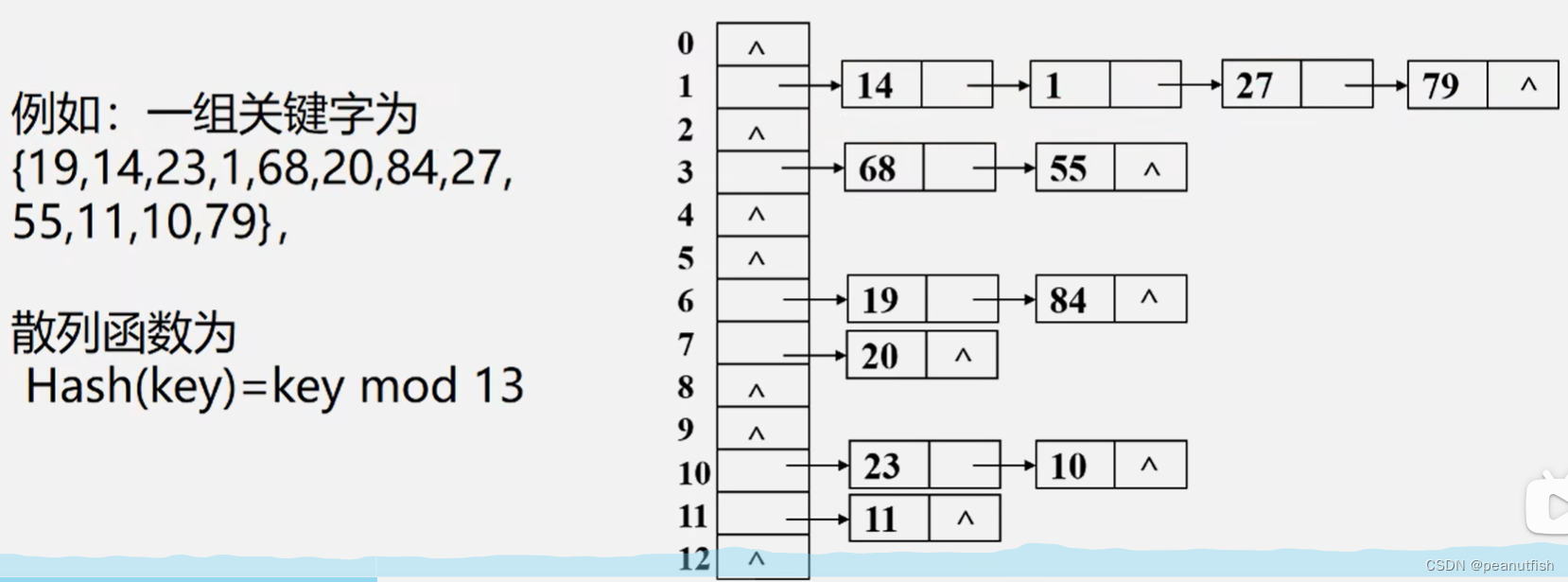
链地址法建立散列表步骤:
Step1: 取数据元素的关键字 key ,计算其散列函数值(地址)。若该地址对应的链表为空,则将该元素插入此链表;否则执行 Step2 解决冲突。
Step2: 根据选择的冲突处理方法,计算关键字 key 的下一个存储地址。若该地址对应的链表为不为空,则利用链表的前插法或后插法将该元素插入此链表。
优点:
-
非同义词不会冲突,无"聚集"现象
-
链表上结点空间动态申请,更适合表长不确定的情况
散列表查找
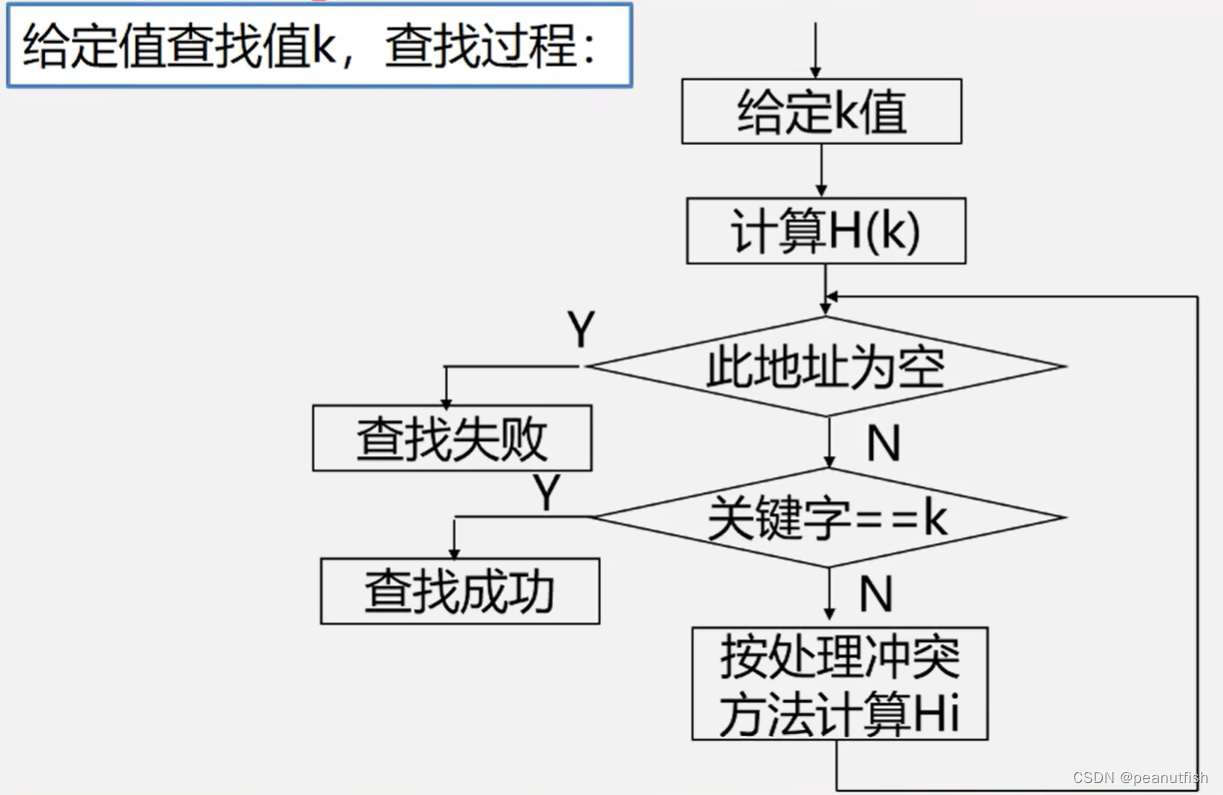
例题:
已知一组关键字(19,14,23,1,68,20,84,27,55,11,10,79)散列函数为: H(key) = key MOD 13,散列表长为 m = 16 ,设每个记录的查找概率相等

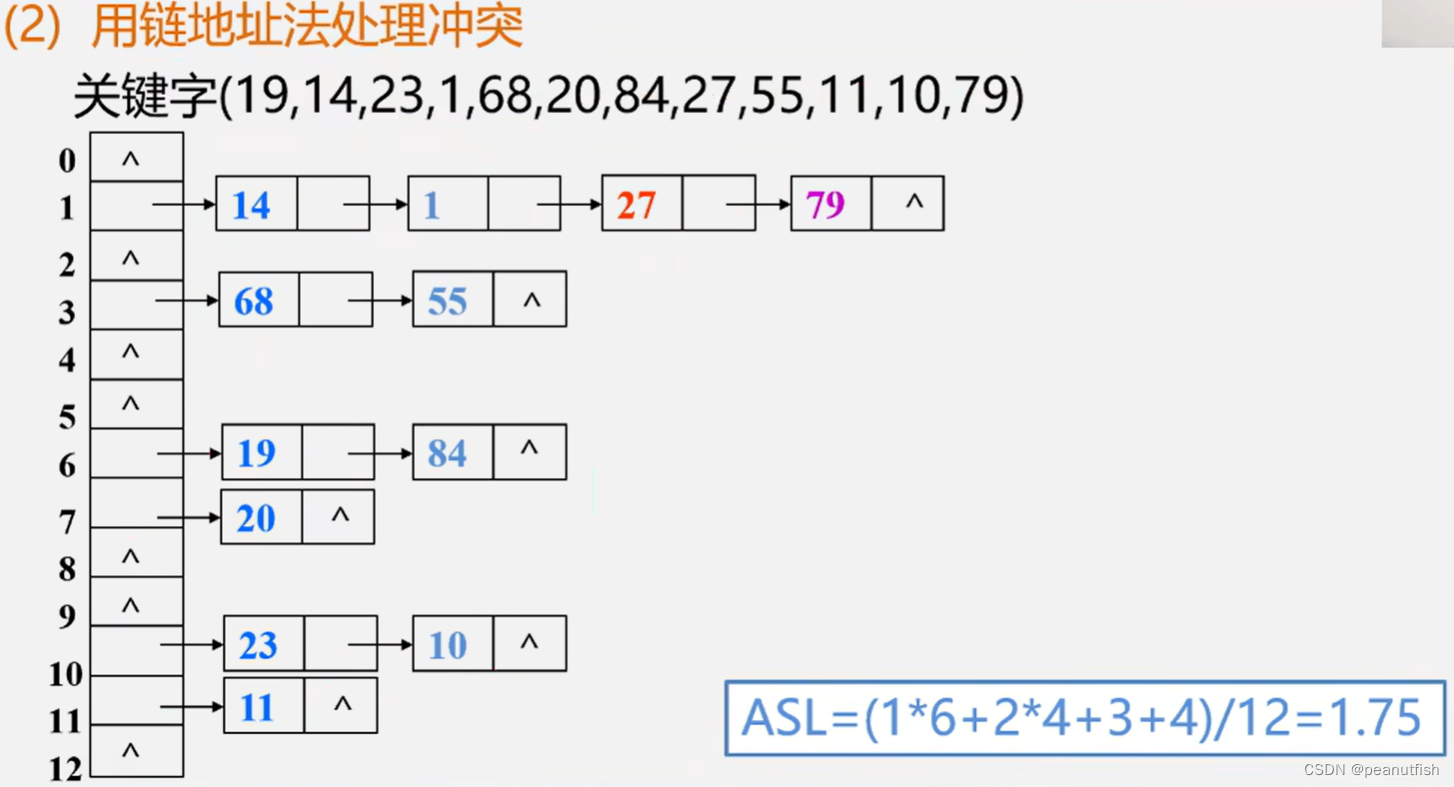
使用平均查找长度 ASL 来衡量查找算法, ASL 取决于:
-
散列函数
-
处理冲突的方法
-
散列表的装填因子α(
α=表中填入记录数/哈希表的长度, α越大,表中记录数越多,说明表装得越满,发生冲突的可能性就越大,查找时比较次数就越多。)
结论:
- 散列表技术具有很好的平均性能,优于一些传统的技术
- 链地址法优于开地址法
- 除留余数法作散列函数优于其它类型函数
TO BE CONTINUED…
相关文章:

数据结构与算法基础(青岛大学-王卓)(8)
哎呀呀,sorry艾瑞波地,这次真的断更一个月了,又发生了很多很多事情,秋风开始瑟瑟了,老父亲身体查出肿瘤了,有病请及时就医,愿每一个人都有一个健康的身体,God bless U and FAMILY. 直…...
【生物信息学】使用谱聚类(Spectral Clustering)算法进行聚类分析
目录 一、实验介绍 二、实验环境 1. 配置虚拟环境 2. 库版本介绍 3. IDE 三、实验内容 0. 导入必要的工具 1. 生成测试数据 2. 绘制初始数据分布图 3. 循环尝试不同的参数组合并计算聚类效果 4. 输出最佳参数组合 5. 绘制最佳聚类结果图 6. 代码整合 一、实验介绍…...

CSS基础语法第二天
目录 一、复合选择器 1.1 后代选择器 1.2 子代选择器 1.3 并集选择器 1.4 交集选择器 1.4.1超链接伪类 二、CSS特性 2.1 继承性 2.2 层叠性 2.3 优先级 基础选择器 复合选择器-叠加 三、Emmet 写法 3.1HTML标签 3.2CSS 四、背景属性 4.1 背景图 4.2 平铺方式 …...
ThreeJS - 封装一个GLB模型展示组件(TypeScript)
一、引言 最近基于Three.JS,使用class封装了一个GLB模型展示,支持TypeScript、支持不同框架使用,具有多种功能。 (下图展示一些基础的功能,可以自行扩展,比如光源等) 二、主要代码 本模块依赖…...

HashMap面试题
1.hashMap底层实现 hashMap的实现我们是要分jdk 1.7及以下版本,jdk1.8及以上版本 jdk 1.7 实现是用数组链表 jdk1.8 实现是用数组链表红黑树, 链表长度大于8(TREEIFY_THRESHOLD)时,会把链表转换为红黑树,…...

Java编程技巧:swagger2、knif4j集成SpringBoot或者SpringCloud项目
目录 1、springbootswagger2knif4j2、springbootswagger3knif4j3、springcloudswagger2knif4j 1、springbootswagger2knif4j 2、springbootswagger3knif4j 3、springcloudswagger2knif4j 注意点: Api注解:Controller类上的Api注解需要添加tags属性&a…...
)
第三章:最新版零基础学习 PYTHON 教程(第九节 - Python 运算符—Python 中的除法运算符)
除法运算符允许您将两个数字相除并返回商,即,第一个数字或左侧的数字除以第二个数字或右侧的数字并返回商。 Python 中的除法运算符 除法运算符有两种类型: 浮点数除法整数除法(向下取整除法)整数相除时,结果四舍五入为最接近的整数,并用符号“//”表示。浮点数“/”…...

【python】导出mysql数据,输出excel!
参考https://blog.csdn.net/pengneng123/article/details/131111713 import pymysql import pandas as pd #import openpyxl import xlsxwriterdb pymysql.connect(host"10.41.241.114", port***,user***,password***,charsetutf8mb4 )cursor db.cursor() #创建游…...

【Java 进阶篇】JDBC ResultSet 遍历结果集详解
在Java数据库编程中,经常需要执行SQL查询并处理查询结果。ResultSet(结果集)是Java JDBC中用于表示查询结果的关键类之一。通过遍历ResultSet,我们可以访问和操作从数据库中检索的数据。本文将详细介绍如何使用JDBC来遍历ResultSe…...
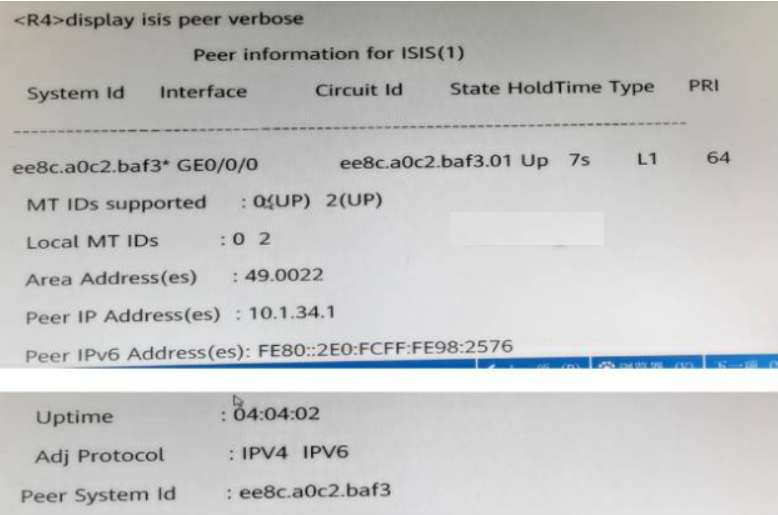
华为数通方向HCIP-DataCom H12-831题库(单选题:161-180)
第161题 某台路由器Router LSA如图所示,下列说法中错误的是? A、本路由器已建立邻接关系 B、本路由器为DR C、本路由支持外部路由引入 D、本路由器的Router ID为10.0.12.1 答案: B 解析: 一类LSA的在transnet网络中link id值为DR的route id ,但Link id的地址不是10.0.12.…...
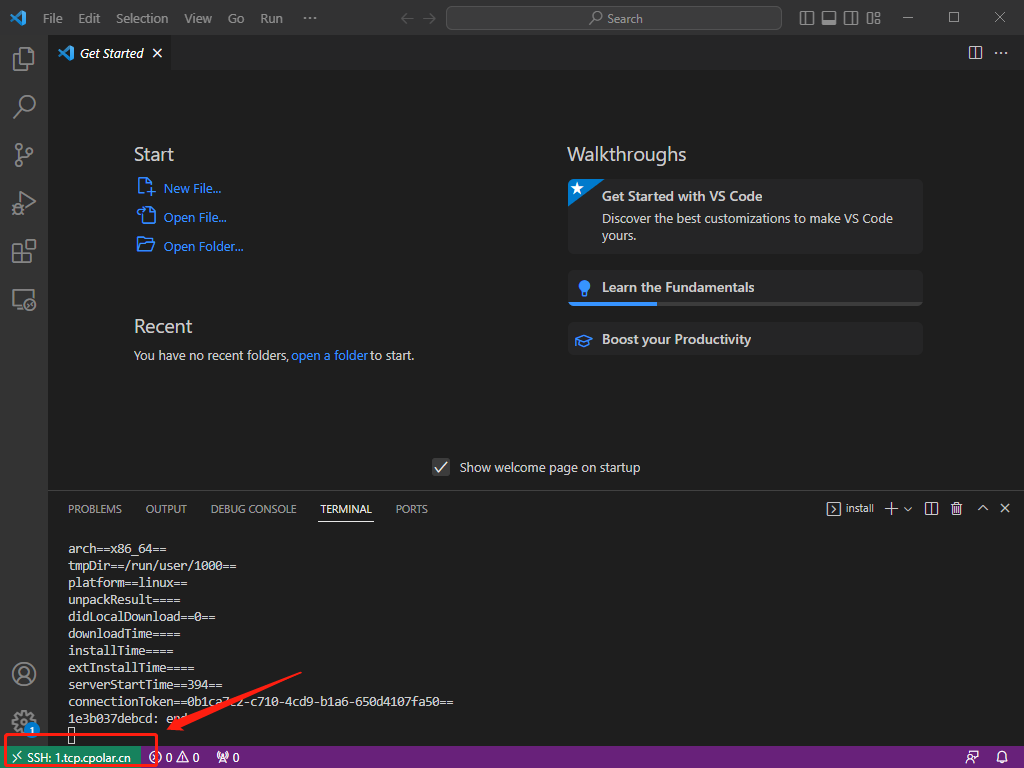
【VsCode】SSH远程连接Linux服务器开发,搭配cpolar内网穿透实现公网访问
文章目录 前言1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 前言 远程…...

java并发编程 守护线程 用户线程 main
经常使用线程,没有对守护线程和用户线程的区别做彻底了解 下面写4个例子来验证一下 源码如下 /* Whether or not the thread is a daemon thread. */ private boolean daemon false;/*** Marks this thread as either a {linkplain #isDaemon daemon} thread*…...
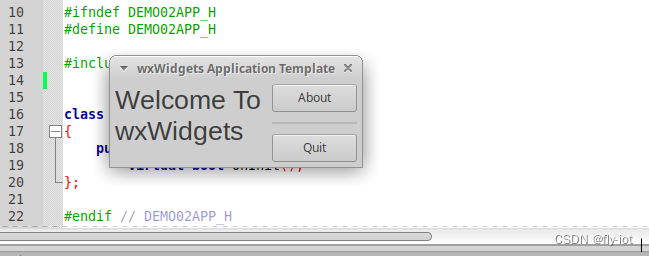
wxWidgets(1):在Ubuntu 环境中搭建wxWidgets 库环境,安装库和CodeBlocks的IDE,可以运行demo界面了,继续学习中
1,选择使用 wxWidgets 框架 选择这个主要是因为完全的开源,不想折腾 Qt的库,而且打包的文件比较大。 网络上面有很多的对比,而且使用QT的人比较多。 但是我觉得wxwidgets 更加偏向 c 语法本身,也有助学习C。 没有太多…...

[VIM]VIM初步学习-3
3-1 编写 vim 配置,我的 vim 我做主_哔哩哔哩_bilibili...
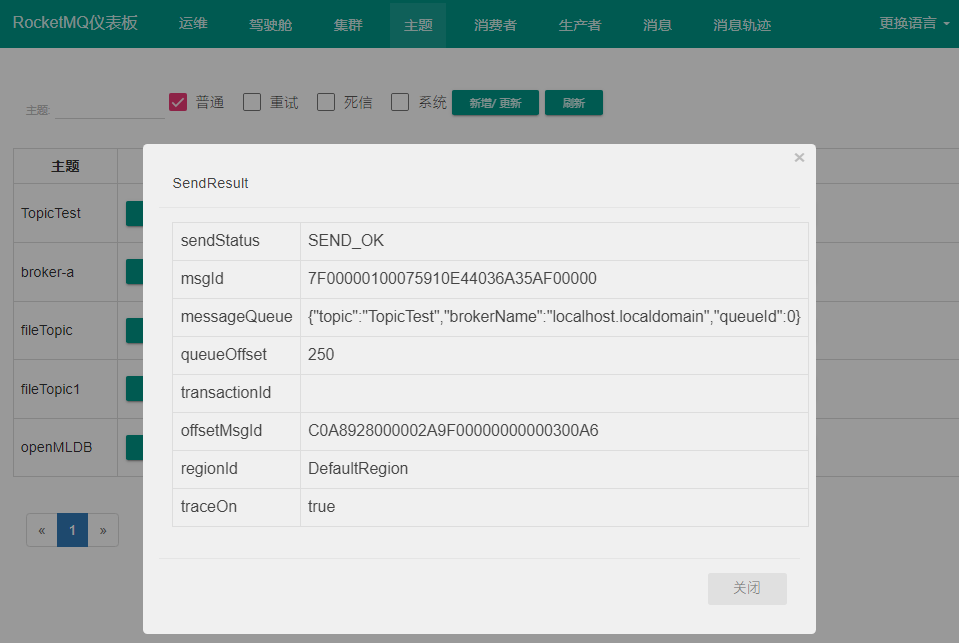
RocketMQ Dashboard说解
RocketMQ Dashboard 是 RocketMQ 的管控利器,为用户提供客户端和应用程序的各种事件、性能的统计信息,支持以可视化工具代替 Topic 配置、Broker 管理等命令行操作。 介绍 功能概览 面板功能运维修改nameserver 地址; 选用 VIPChannel驾驶舱查看 …...
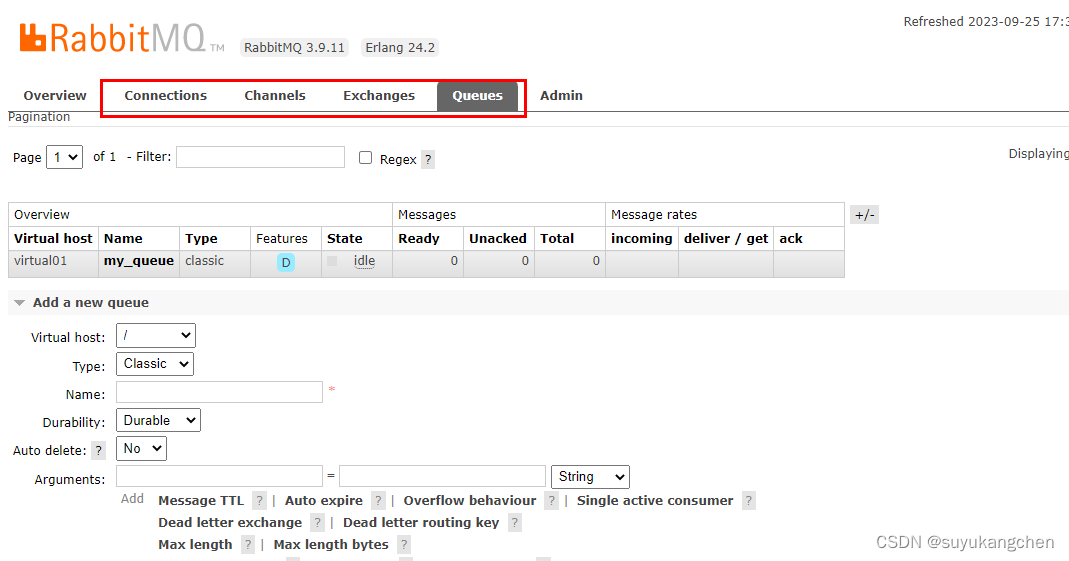
【RabbitMQ实战】05 RabbitMQ后台管理
一、多租户与权限 1.1 vhost的概念 每一个 RabbitMQ服务器都能创建虚拟的消息服务器,我们称之为虚拟主机(virtual host),简称为 vhost。每一个 vhost本质上是一个独立的小型RabbitMQ服务器,拥有自己独立的队列、交换器及绑定关系等,并且它拥…...

PHP8中final关键字的应用-PHP8知识详解
在PHP8中,final的中文含义是最终的、最后的意思。被final修饰过的类和方法就是“最终的版本”。 如果关键字final放在类的前面,则表示该类不能被继承。 如果关键字final放在方法的前面,则表示该 方法不能被重新定义。 如果有一个类的格式为…...

基于Java的校园失物招领平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

〔024〕Stable Diffusion 之 模型训练 篇
✨ 目录 🎈 训练集准备🎈 训练集预处理🎈 数据清洗🎈 下载训练源码🎈 训练文件配置🎈 脚本运行🎈 实战测试🎈 训练集准备 声明: 该文中所涉及到的女神图片均来自于网络,仅用作技术教程演示,图片已码一般同一个训练集需要准备 20~40 张不同角度的照片,当然可…...

【MySQL入门到精通-黑马程序员】MySQL基础篇-DML
文章目录 前言一、DML-介绍二、DML-添加数据三、DML-修改数据四、DML-删除数据总结 前言 本专栏文章为观看黑马程序员《MySQL入门到精通》所做笔记,课程地址在这。如有侵权,立即删除。 一、DML-介绍 DML(Data Manipulation Language…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
