Drift plus penalty 漂移加惩罚Part1——介绍和工作原理
文章目录
- 正文
- Methodology 方法论
- Origins and applications 起源和应用
- How it works 它是怎样工作的
- The stochastic optimization problem 随机优化问题
- Virtual queues 虚拟队列
- The drift-plus-penalty expression 漂移加惩罚表达式
- Drift-plus-penalty algorithm
- Approximate scheduling 近似调度
- 参考资料
正文
在概率论的数学理论中,漂移加惩罚法被用于优化排队网络和其他随机系统。
该技术用于稳定排队网络,同时最小化网络惩罚函数的平均时间。它可用于优化性能目标,如时间平均功率、吞吐量和吞吐量效用。在不需要最小化惩罚的特殊情况下,当目标是在多跳网络中设计稳定的路由策略时,该方法可以简化为背压路由。漂移加惩罚法也可用于最小化受时间平均约束的随机过程对其他随机过程集合的时间平均。这是通过定义一组适当的虚拟队列来实现的。它还可以用于生成凸优化问题的时间平均解。
Methodology 方法论
漂移加惩罚方法适用于离散时间时隙 t t t 在 0 , 1 , 2 , … {0,1,2,…} 0,1,2,… 中运行的排队系统。首先,非负函数 L ( t ) L(t) L(t) 被定义为时间t时所有队列状态的标量度量。函数 L ( t ) L(t) L(t) 通常被定义为时间 t t t 时所有队列大小的平方和,称为李雅普诺夫函数。李亚普诺夫漂移定义如下:
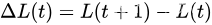
每个时隙 t t t,观察当前队列状态,并采取控制动作贪婪地最小化以下漂移+惩罚表达式的边界:

其中 p ( t ) p(t) p(t) 是罚函数 V V V 是一个非负的权值。可以选择 V V V 参数,以确保 p ( t ) p(t) p(t) 的时间平均值任意接近最优值,并在平均队列大小上进行相应的权衡。与背压路由一样,这种方法通常不需要了解工作到达和网络移动性的概率分布。
Origins and applications 起源和应用
当 V = 0 V=0 V=0,该方法简化为贪婪地最小化李雅普诺夫漂移。这就是最初由Tassiulas和Ephremides开发的背压路由算法(也称为最大权重算法)。
Neely和Neely, Modiano, Li在漂移表达式中加入了 V p ( t ) Vp(t) Vp(t) 项,以在稳定网络的同时最大化吞吐量效用函数。为此,惩罚 p ( t ) p(t) p(t) 被定义为 − 1 -1 −1 倍。 这种漂移加惩罚技术后来被用于最小化平均功率并优化其他惩罚和奖励指标。
该理论主要用于优化通信网络,包括无线网络、自组织移动网络和其他计算机网络。然而,数学技术可以应用于其他随机系统的优化和控制,包括智能电网中的可再生能源分配和产品装配系统的库存控制。
How it works 它是怎样工作的
本节展示如何使用漂移加惩罚方法来最小化受其他函数集合的时间平均约束的函数 p ( t ) p(t) p(t) 的时间平均。(就是说要最小化 p ( t ) p(t) p(t) 的时间平均,但是同时受到其它时间平均的约束)。
The stochastic optimization problem 随机优化问题
考虑一个离散时间系统,它在规范化时隙 t = 0 , 1 , 2 , … t={0,1,2,…} t=0,1,2,… 上变化。定义 p ( t ) p(t) p(t) 为需要将时间平均值最小的函数,称为惩罚函数。假设 p ( t ) p(t) p(t) 的时间平均值的最小化必须在 K K K 个其他函数集合的时间平均值约束下完成:
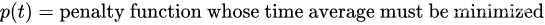
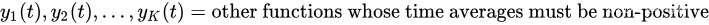
每个时隙 t t t,网络控制器观察到一个新的随机事件。然后,它根据对该事件的了解做出控制动作。将 p ( t ) p(t) p(t) 和 y i ( t ) y_i(t) yi(t) 的值确定为随机事件和时隙 t t t 的控制作用的函数:
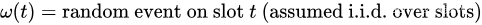
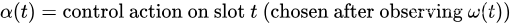
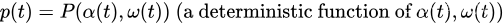
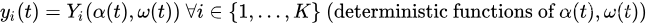
小写符号 p ( t ) p(t) p(t), y i ( t ) y_i(t) yi(t) 和大写符号 P ( ) P() P(), Y i ( ) Y_i() Yi() 用于区分惩罚值和根据随机事件和时隙 t t t 的控制作用确定这些值的函数。
假设随机事件 ω ( t ) \omega (t) ω(t) 在一些抽象的事件集合 Ω Ω Ω 中取值。
假设控制动作 α ( t ) \alpha (t) α(t) 是在某个包括控制项抽象集合 A A A 中选择的。
集合 Ω \Omega Ω 和 A A A 是任意的,可以是有限的也可以是无限的。
例如, A A A 可以是抽象元素的有限列表,实值向量的不可数无限(可能是非凸的)集合,等等。函数 P ( ) P() P(), Y _ i ( ) Y_i() Y_i() 也是任意的,不需要连续性或凸性假设。
以通信网络中的随机事件为例 ω ( t ) \omega (t) ω(t) 可以是一个向量,它包含每个节点时隙 t t t 时的到达信息和每个链路的时隙 t t t 时的信道状态信息。
控制动作 α ( t ) \alpha (t) α(t) 可以是包含每个节点的路由和传输决策的向量。
函数 P ( ) P() P() 和 Y _ i ( ) Y_i() Y_i() 可以表示与时隙 t t t 的控制动作和通道条件相关的功率消耗或吞吐量。
为了说明简单,假设 P ( ) P() P() 和 Y i ( ) Y_i() Yi() 函数是有界的。进一步假设随机事件过程 ω ( t ) \omega(t) ω(t) 在槽 t t t 上独立且同分布,具有一些可能未知的概率分布。目标是设计一个策略,使控制行动随着时间的推移,以解决以下问题:

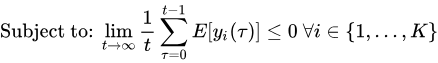
即最小化惩罚项的时间平均值,同时维持队列的稳定。
自始至终都假定这个问题是可行的。也就是说,假设存在一种算法可以满足所有 K K K 个期望约束。
上述问题以抽象过程 y i ( t ) y_i(t) yi(t) 非正的时间平均期望的标准形式提出了每个约束。这种方法不会失去通用性。例如,假设某人希望某个过程 a ( t ) a(t) a(t)的时间平均期望小于或等于给定常数 c c c。那么可以定义一个新的惩罚函数 y ( t ) = a ( t ) − c y(t) = a(t) - c y(t)=a(t)−c,并且期望的约束等价于 y ( t ) y(t) y(t)的时间平均期望是非正的。同样,假设有两个过程 a ( t ) a(t) a(t)和 b ( t ) b(t) b(t),并且希望 a ( t ) a(t) a(t)的时间平均期望小于或等于 b ( t ) b(t) b(t)的时间平均期望。这个约束通过定义一个新的惩罚函数 y ( t ) = a ( t ) − b ( t ) y(t) = a(t) - b(t) y(t)=a(t)−b(t)写成标准形式。上述问题寻求最小化抽象惩罚函数 p ′ ( t ) ′ p'(t)' p′(t)′的时间平均值。这可以通过定义 p ( t ) = − r ( t ) p(t) = - r(t) p(t)=−r(t)来最大化某些理想奖励函数 r ( t ) r(t) r(t)的时间平均值。
Virtual queues 虚拟队列
对于 { 1 , … , K } \{1,…, K\} {1,…,K}中的每个约束 i i i,定义一个在时隙 t = { 0 , 1 , 2 , . . . } t=\{0,1,2,...\} t={0,1,2,...} 上动态的虚拟队列,如下:
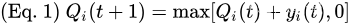
对所有 i ∈ { 1 , . . . , K } i∈\{1,...,K\} i∈{1,...,K} 初始化 Q i ( 0 ) = 0 Q_i(0) = 0 Qi(0)=0 。该更新方程与虚拟离散时间队列积压 Q i ( t ) Q_i(t) Qi(t)相同,其中 y i ( t ) y_i(t) yi(t) 为时隙 t t t 上新到达和新服务机会之间的差。直观地说,稳定这些虚拟队列确保约束函数的时间平均值小于或等于零,因此满足期望的约束。要准确地理解这一点,请注意(式1)意味着:
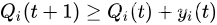
因此
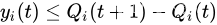
利用伸缩和定律对前 t t t 个槽求和,可得:
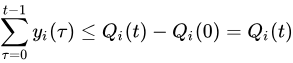
除以t,取期望:
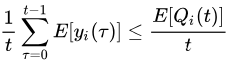
因此,当对于所有 i ∈ { 1 , … K } i∈\{1,…K\} i∈{1,…K} 中所有i满足下列条件时,问题的期望约束得到满足:

满足上述极限方程的队列 Q i ( t ) Q_i(t) Qi(t) 被称为是平均速率稳定的。
The drift-plus-penalty expression 漂移加惩罚表达式
为了稳定队列,定义Lyapunov函数 L ( t ) L(t) L(t)作为槽位 t t t上队列积压总量的度量:
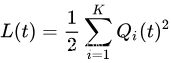
将排队方程(Eq. 1)平方,得到每个 i ∈ { 1 , . . . , K } i∈\{1,...,K\} i∈{1,...,K}的队列的下列边界:
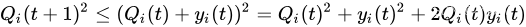
因此,
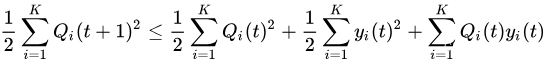
由此得出
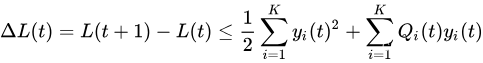
现在把 B B B 定义为一个正常数,它是上面不等式右边第一项的上界。因为 y i ( t ) y_i(t) yi(t) 的值是有界的,所以存在这样一个常数。则:

两边同时加上 V p ( t ) Vp(t) Vp(t),得到漂移加惩罚表达式的边界如下:
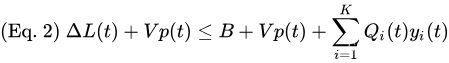
漂移+惩罚算法(定义如下)使控制动作在每个槽 t t t上贪婪地最小化上述不等式的右侧。
直观地说,仅采取最小化漂移的操作在队列稳定性方面是有益的,但不会最小化惩罚项的时间平均值。仅仅采取最小化惩罚的措施并不一定会稳定队列。
因此,采取最小化加权总和的动作同时包含了队列稳定性和惩罚最小化的目标。可以调整权重V,以或多或少地强调惩罚最小化,这将导致性能的权衡。
Drift-plus-penalty algorithm
让 A A A 是所有可能的控制动作的抽象集合。
在每个时隙 t t t,观察随机事件和当前队列值:
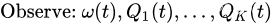
给定槽 t t t 的这些观察结果,贪婪地选择一个控制动作 α ( t ) ∈ A \alpha (t)\in A α(t)∈A以最小化以下表达式:
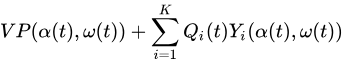
然后根据(式1)为 i ∈ { 1 , … , K } i \in \{1,…, K\} i∈{1,…,K} 更新队列,对时隙 t + 1 t+1 t+1 重复此过程。
注意,当时隙 t t t 最小化的控制动作时,在槽 t t t 上观察到的随机事件和队列积压充当给定的常量。因此,每个槽都涉及对集合 A A A 的最小化控制动作的确定性搜索。该算法的一个关键特征是它不需要了解随机事件过程的概率分布。
Approximate scheduling 近似调度
上述算法涉及在抽象集合 A A A 上寻找一个函数的最小值。在一般情况下,最小值可能不存在,或者可能很难找到。
因此,假设算法以如下近似方式实现是有用的:定义 C C C为非负常数,并假设对于所有槽 t t t,在集合A中选择的控制动作 α ( t ) \alpha (t) α(t)满足:
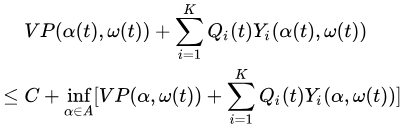
这样的控制作用称为 C-加性近似 。 C = 0 C = 0 C=0 的情况对应于每个槽 t t t 上所需表达式的精确最小化。
参考资料
https://en.wikipedia.org/wiki/Drift_plus_penalty
相关文章:
Drift plus penalty 漂移加惩罚Part1——介绍和工作原理
文章目录 正文Methodology 方法论Origins and applications 起源和应用How it works 它是怎样工作的The stochastic optimization problem 随机优化问题Virtual queues 虚拟队列The drift-plus-penalty expression 漂移加惩罚表达式Drift-plus-penalty algorithmApproximate sc…...

(四)动态阈值分割
文章目录 一、基本概念二、实例解析 一、基本概念 基于局部阈值分割的dyn_threshold()算子,适用于一些无法用单一灰度进行分割的情况,如背景比较复杂,有的部分比前景目标亮,或者有的部分比前景目标暗;又比如前景目标包…...

jvm介绍
1. JVM是什么 JVM是Java Virtual Machine的缩写,即咱们经常提到的Java虚拟机。虚拟机是一种抽象化的计算机,有着自己完善的硬件架构,如处理器、堆栈等,具体有什么咱们不做了解。目前我们只需要知道想要运行Java文件,必…...
数据结构与算法课后题-第三章(顺序队和链队)
#include <iostream> //引入头文件 using namespace std;typedef int Elemtype;#define Maxsize 5 #define ERROR 0 #define OK 1typedef struct {Elemtype data[Maxsize];int front, rear;int tag; }SqQueue;void InitQueue(SqQueue& Q) //初始化队列 {Q.rear …...
SSM - Springboot - MyBatis-Plus 全栈体系(十六)
第三章 MyBatis 三、MyBatis 多表映射 2. 对一映射 2.1 需求说明 根据 ID 查询订单,以及订单关联的用户的信息! 2.2 OrderMapper 接口 public interface OrderMapper {Order selectOrderWithCustomer(Integer orderId); }2.3 OrderMapper.xml 配置…...

k8s--storageClass自动创建PV
文章目录 一、storageClass自动创建PV1.1 安装NFS1.2 创建nfs storageClass1.3 测试自动创建pv 一、storageClass自动创建PV 这里使用NFS实现 1.1 安装NFS 安装nfs-server: sh nfs_install.sh /mnt/data03 10.60.41.0/24nfs_install.sh #!/bin/bash### How to i…...

7.3 调用函数
前言: 思维导图: 7.3.1 函数调用的形式 我的笔记: 函数调用的形式 在C语言中,调用函数是一种常见的操作,主要有以下几种调用方式: 1. 函数调用语句 此时,函数调用独立存在,作为…...

如果使用pprof来进行性能的观测和优化
1. 分析性能瓶颈 在开始优化之前,首先需要确定你的程序的性能瓶颈在哪里。使用性能分析工具(例如 Go 的内置 pprof 包)来检测程序中消耗时间和内存的地方。这可以帮助你确定需要优化的具体部分。 2. 选择适当的数据结构和算法 选择正确的数…...
在移动固态硬盘上安装Ubuntu系统和ROS2
目录 原视频准备烧录 原视频 b站鱼香ros 准备 1.在某宝上买一个usb移动固态硬盘或固态U盘,至少64G 2.下载鱼香ros烧录工具 下载第二个就行了,不然某网盘的速度下载全部要一天 下载后,选择FishROS2OS制作工具压缩包,进行解压…...

【iptables 实战】02 iptables常用命令
一、iptables中基本的命令参数 -P 设置默认策略-F 清空规则链-L 查看规则链-A 在规则链的末尾加入新规则-I num 在规则链的头部加入新规则-D num 删除某一条规则-s 匹配来源地址IP/MASK,加叹号“!”表示除这个IP外-d 匹配目标地址-i 网卡名称 匹配从这块…...

webview_flutter
查看webview内核 https://liulanmi.com/labs/core.html h5中获取设备 https://cloud.tencent.com/developer/ask/sof/105938013 https://developer.mozilla.org/zh-CN/docs/Web/API/Navigator/mediaDevices web资源部署后navigator获取不到mediaDevices实例的解决方案&…...

【GESP考级C++】1级样题 闰年统计
GSEP 1级样题 闰年统计 题目描述 小明刚刚学习了如何判断平年和闰年,他想知道两个年份之间(包含起始年份和终止年份)有几个闰年。你能帮帮他吗? 输入格式 输入一行,包含两个整数,分别表示起始年份和终止…...
CentOS密码重置
背景: 我有一个CentOS虚拟机,但是密码忘记了,偶尔记起可以重置密码,于是今天尝试记录一下,又因为我最近记性比较差,所以必须要记录一下。 过程: 1、在引导菜单界面(grubÿ…...
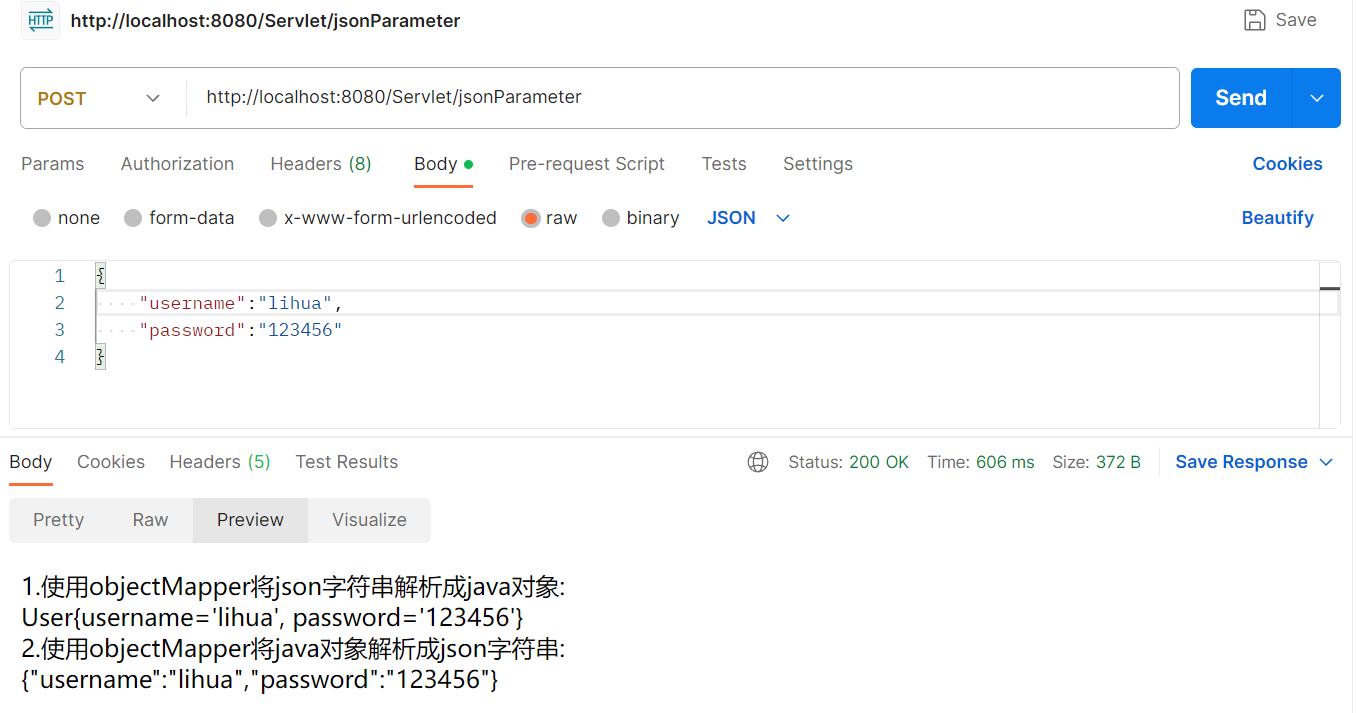
Tomcat Servlet
Tomcat & Servlet 一、What is “Tomcat”?二、 What is “Servlet”?1、HttpServlet2、HttpServletRequest3、HttpServletResponse 一、What is “Tomcat”? Tomcat 本质上是一个基于 TCP 协议的 HTTP 服务器。我们知道HTTP是一种应用层协议,是 HTTP 客户端…...
国庆day2---select实现服务器并发
select.c: #include <myhead.h>#define ERR_MSG(msg) do{\fprintf(stderr,"__%d__:",__LINE__);\perror(msg);\ }while(0)#define IP "192.168.1.3" #define PORT 8888int main(int argc, const char *argv[]) {//创建报式套接字socketi…...
Grafana 开源了一款 eBPF 采集器 Beyla
eBPF 的发展如火如荼,在可观测性领域大放异彩,Grafana 近期也发布了一款 eBPF 采集器,可以采集服务的 RED 指标,本文做一个尝鲜介绍,让读者有个大概了解。 eBPF 基础介绍可以参考我之前的文章《eBPF Hello world》。理…...
亲测可用国产GPT人工智能
分享一些靠谱、可用、可以白嫖的GPT大模型。配合大模型,工作效率都会极大提升。 清华大学ChatGLM 官网: 智谱清言中国版对话语言模型,与GLM大模型进行对话。https://chatglm.cn/开源的、支持中英双语的1300亿参数的对话语言模型࿰…...
)
适配器模式详解和实现(设计模式 四)
适配器模式将一个类的接口转换成客户端所期望的另一个接口,解决由于接口不兼容而无法进行合作的问题。 设计基本步骤 1. 创建目标接口(Target Interface),该接口定义了客户端所期望的方法。 2.创建被适配类(Adaptee…...
IDEA的使用
文章目录 1.IDEA配置1.1 idea界面说明1.2 git1.3 JDK1.4 maven1.5 Tomcat1.6 idea设置编码格式1.7 vscodenodejs1.8 windows下安装redis 2. IDEA问题2.1 setAttribute方法爆红2.2 idea cannot download sources解决办法2.3 springboot项目跑起来不停run 3. vscode3.1 vscode显示…...

CSS详细基础(二)文本样式
插播一条CSS的工作原理: CSS是一种定义样式结构如字体、颜色、位置等的语言,被用于描述网页上的信息格式化和显示的方式。CSS样式可以直接存储于HTML网页或者单独的样式单文件。无论哪一种方式,样式单包含将样式应用到指定类型的元素的规则。…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
