数据结构—归并排序-C语言实现
引言:归并排序跟快速排序一样,都运用到了分治的算法,但是归并排序是一种稳定的算法,同时也具备高效,其时间复杂度为O(N*logN)
算法图解:
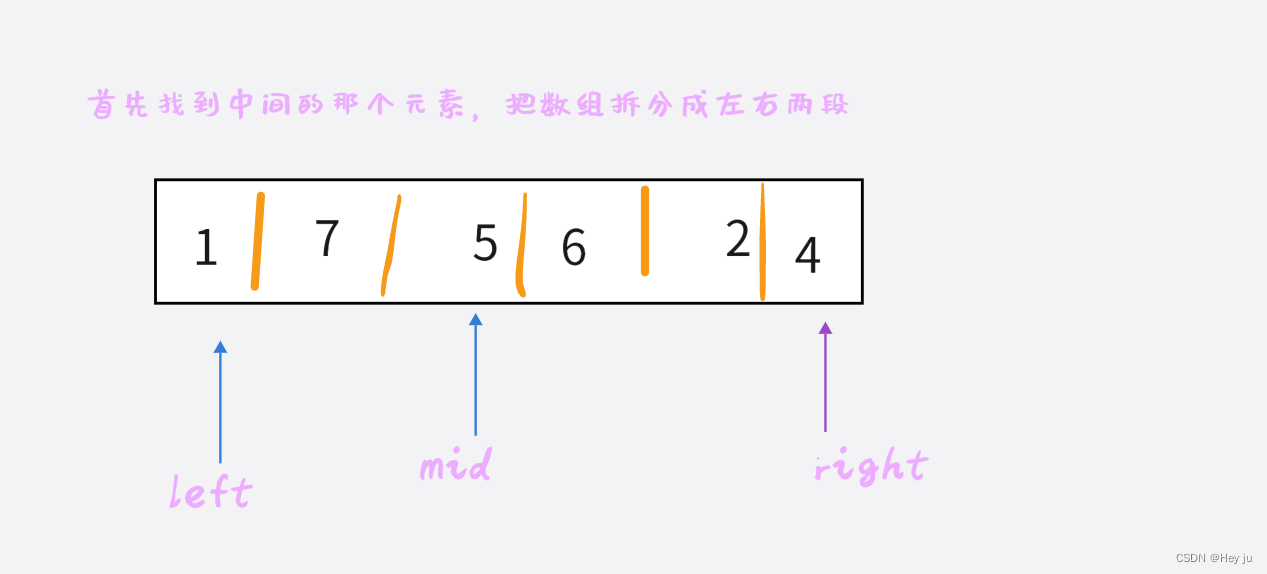
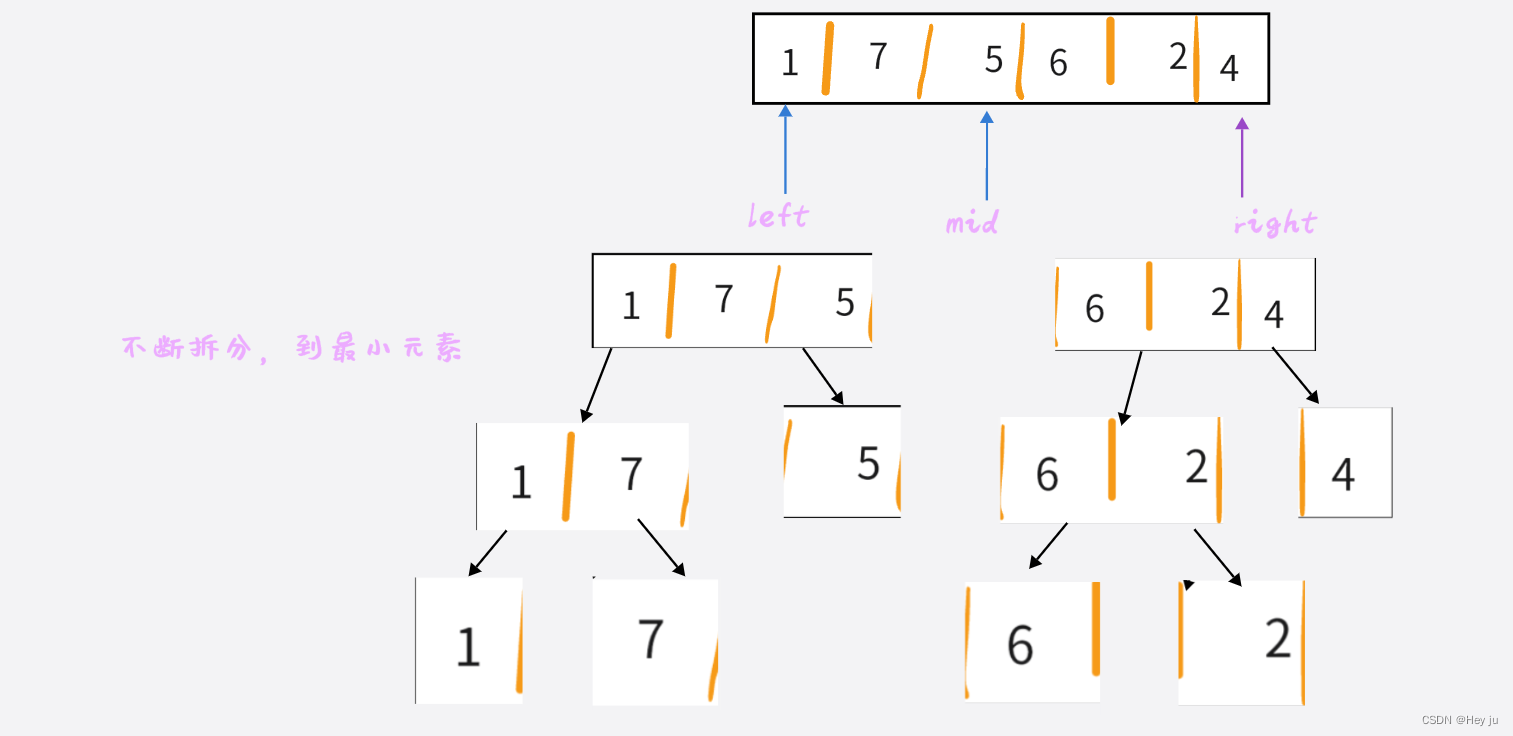
然后开始归并:
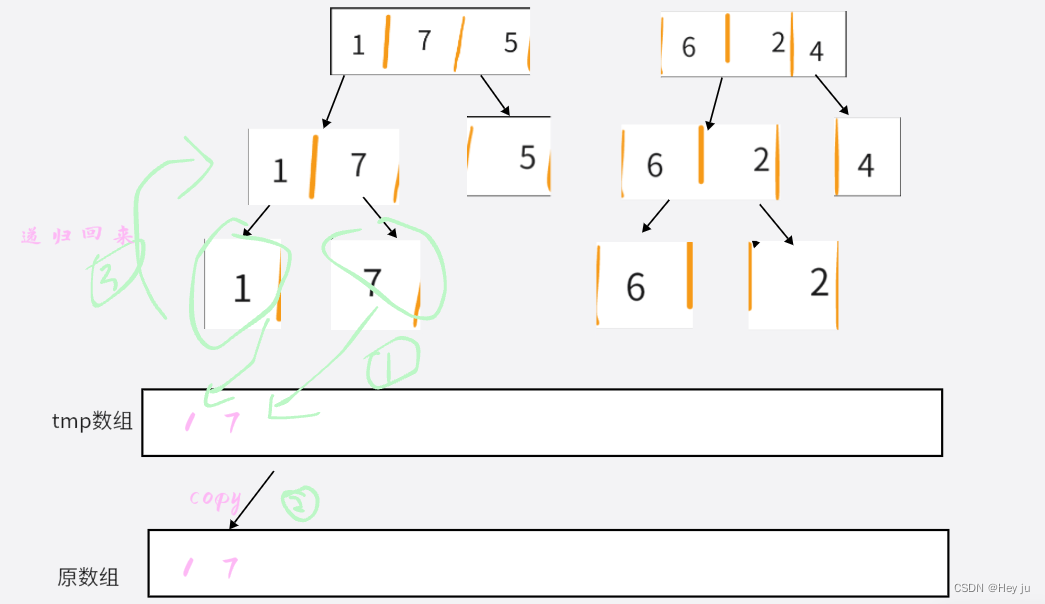
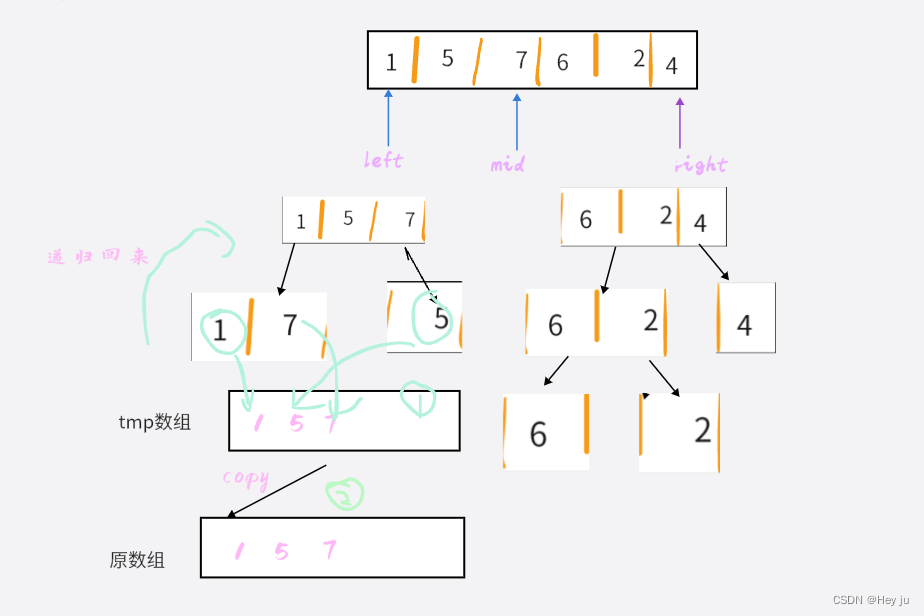 就是这个思想,拆成最小子问题后再进行归并(两个有序数组的排序问题)
就是这个思想,拆成最小子问题后再进行归并(两个有序数组的排序问题)
下面是代码:
void merge_sort(int* arry, int size) {//保证接口一致性,再调子函数assert(arry);int* tmp = (int*)malloc(sizeof(int) * size);_merge(arry, 0, size - 1,tmp);//_merge2(arry, 0, size - 1, tmp);free(tmp);
}
void _merge(int* arry, int left, int right, int* tmp) {if (right - left <= 0)return;int mid = left + (right - left >> 1);//找到中间值//递归,拆分子问题_merge(arry, left, mid, tmp);_merge(arry, mid + 1, right, tmp);merge_arry(arry, left, mid, mid + 1, right, tmp);
}
void merge_arry(int* arry, int begin1, int end1, int begin2, int end2, int* tmp) {int index = begin1;int left = begin1;int right = end2;while (begin1 <= end1 && begin2 <= end2) {if (arry[begin1] < arry[begin2]) {tmp[index++] = arry[begin1++];}else {tmp[index++] = arry[begin2++];}}if (begin1 <= end1) {for (int i = begin1; i <= end1; i++) {tmp[index++] = arry[i];}}else {for (int i = begin2; i <= end2; i++) {tmp[index++] = arry[i];}}//再拷贝回原数组for (int i = left; i <= right; i++) {arry[i] = tmp[i];}
}上面是它的递归实现,那么思考如何使用非递归实现呢?
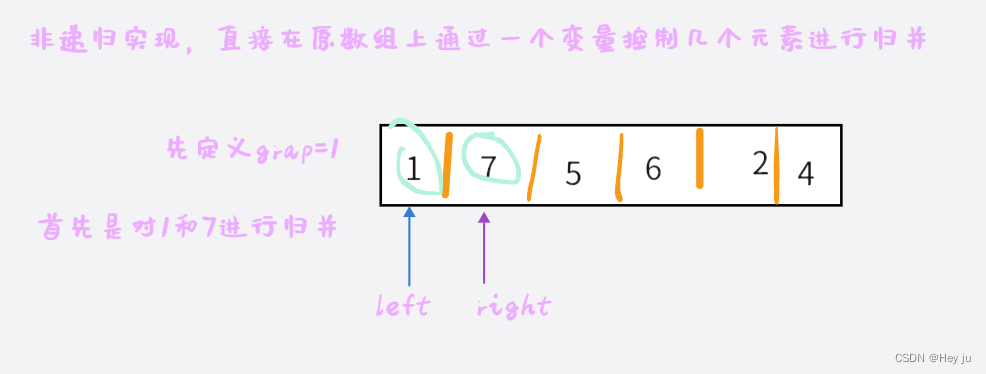
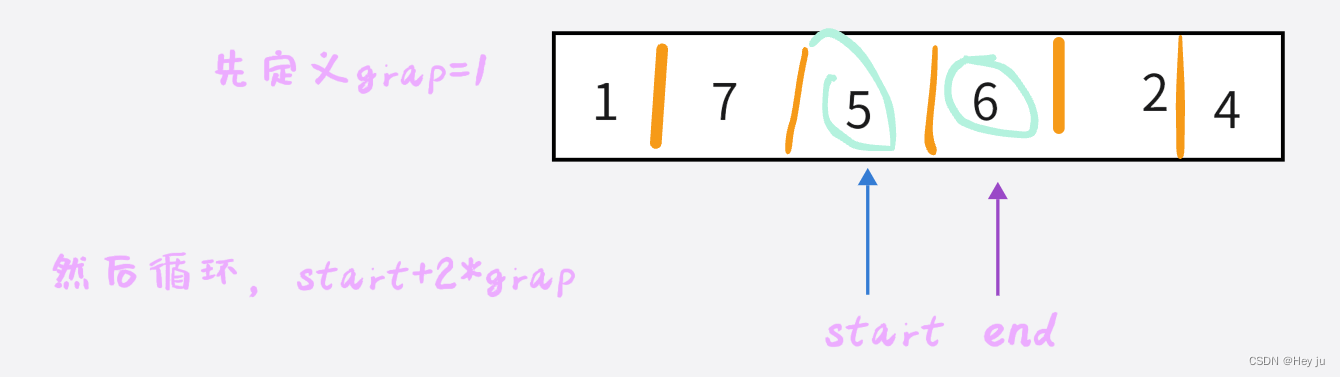
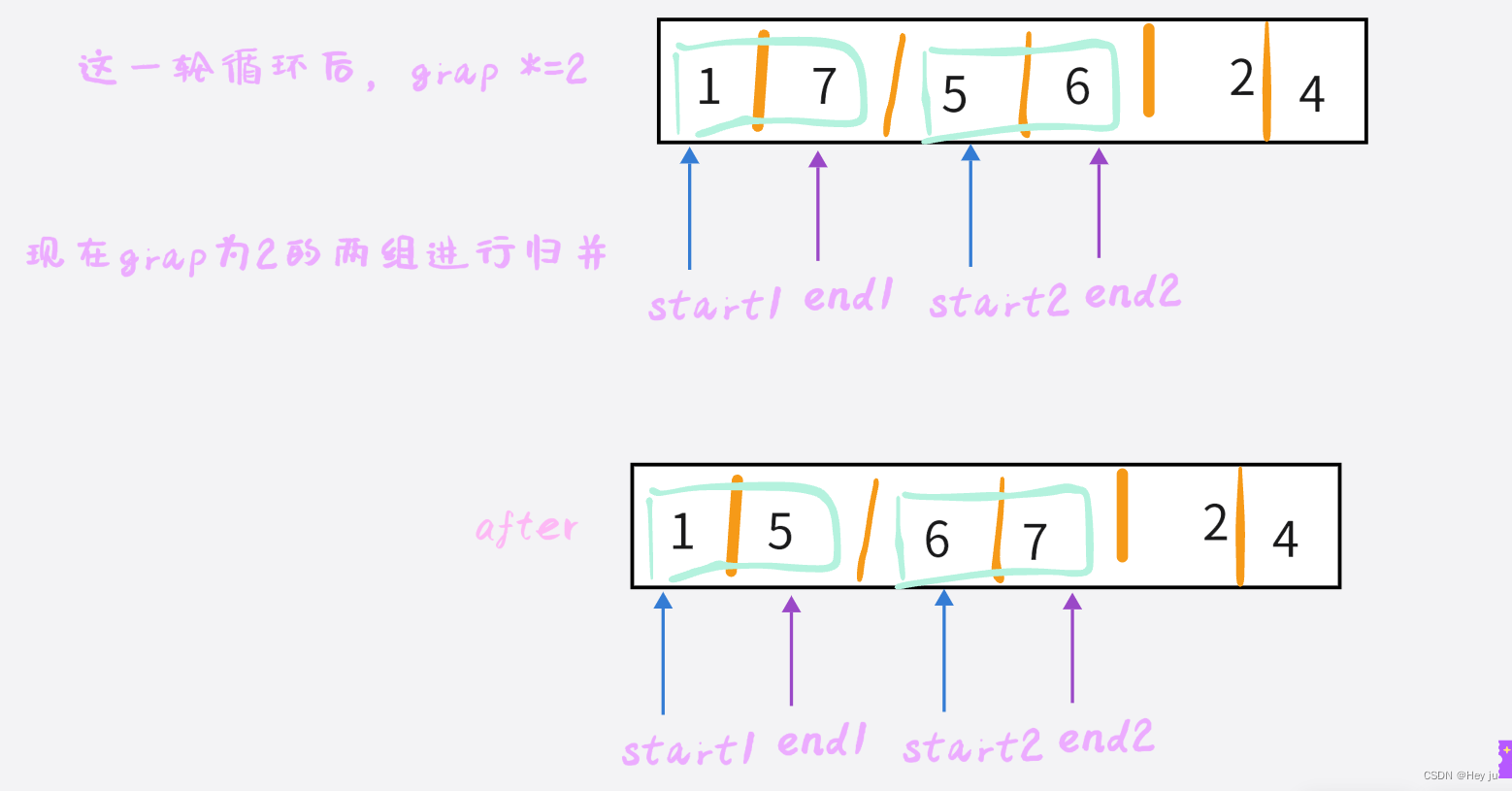 同时要控制grap的循环次数,grap小于等于数组大小即可
同时要控制grap的循环次数,grap小于等于数组大小即可
下面是代码:
void _merge2(int* arry, int left, int right, int* tmp) {int grap = 1;while (grap<=right+1) {for (int i = left; i <= right; i += 2 * grap) {int begin1 = i, end1 = i + grap - 1;int begin2 = i + grap, end2 = i + 2 * grap - 1;if (end1 > right)end1 = right;if (end2 > right)end2 = right;merge_arry(arry, begin1, end1, begin2, end2, tmp);}grap = grap * 2;}}
void merge_sort(int* arry, int size) {assert(arry);int* tmp = (int*)malloc(sizeof(int) * size);//_merge(arry, 0, size - 1,tmp);_merge2(arry, 0, size - 1, tmp);free(tmp);
}相关文章:

数据结构—归并排序-C语言实现
引言:归并排序跟快速排序一样,都运用到了分治的算法,但是归并排序是一种稳定的算法,同时也具备高效,其时间复杂度为O(N*logN) 算法图解: 然后开始归并: 就是这个思想,拆成最小子问题…...
Multiple CORS header ‘Access-Control-Allow-Origin‘ not allowed
今天在修改天天生鲜超市项目的时候,因为使用了前后端分离模式,前端通过网关统一转发请求到后端服务,但是第一次使用就遇到了问题,比如跨域问题: 但是,其实网关里是有配置跨域的,只是忘了把前端项…...
msvcp100.dll丢失怎样修复,msvcp100.dll丢失问题全面解析
msvcp100.dll是一个动态链接库文件,属于 Microsoft Visual C Redistributable 的一个组件。它包含了 C 运行时库,这些库在运行程序时会被加载到内存中。msvcp100.dll文件的主要作用是为基于 Visual C 编写的程序提供必要的运行时支持。 当您运行一个基于…...
最新AI智能问答系统源码/AI绘画系统源码/支持GPT联网提问/Prompt应用+支持国内AI提问模型
一、AI创作系统 SparkAi创作系统是基于国外很火的ChatGPT进行开发的AI智能问答系统和AI绘画系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图…...
全连接网络实现回归【房价预测的数据】
也是分为data,model,train,test import torch import torch.nn as nn import torch.nn.functional as F import torch.optim as optimclass FCNet(nn.Module):def __init__(self):super(FCNet,self).__init__()self.fc1 nn.Linear(331,200)s…...
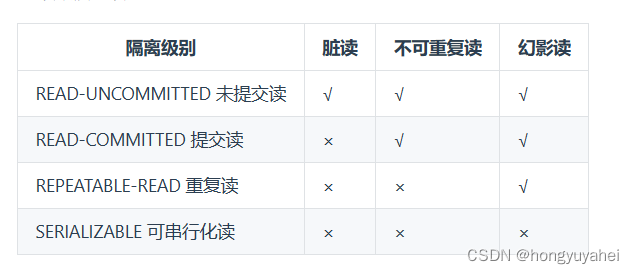
mysql八股
1、请你说说mysql索引,以及它们的好处和坏处 检索效率、存储资源、索引 索引就像指向表行的指针,是一个允许查询操作快速确定哪些行符合WHERE子句中的条件,并检索到这些行的其他列值的数据结构索引主要有普通索引、唯一索引、主键索引、外键…...
(附MATLAB代码实现))
MATLAB算法实战应用案例精讲-【优化算法】狐猴优化器(LO)(附MATLAB代码实现)
代码实现 MATLAB LO.m %======================================================================= % Lemurs Optimizer: A New Metaheuristic Algorithm % for Global Optimization (LO)% This work is published in Journal of "Applied …...

C#WPF动态资源和静态资源应用实例
本文实例演示C#WPF动态资源和静态资源应用 一、资源概述 静态资源(StaticResource)指的是在程序载入内存时对资源的一次性使用,之后就不再访问这个资源了。 动态资源(DynamicResource)指的是在程序运行过程中然会去访问资源。 WPF中,每个界面元素都含有一个名为Resources…...

游戏逆向中的 NoClip 手段和安全应对方式
文章目录 墙壁边界寻找碰撞 NoClip 是一种典型的黑客行为,允许你穿过墙壁,所以 NoClip 又可以认为是避免碰撞体积的行为 墙壁边界 游戏中设置了碰撞体作为墙壁边界,是 玩家对象 和墙壁发生了碰撞,而不是 相机 玩家对象有他的 X…...
nodejs+vue流浪猫狗救助领养elementui
第三章 系统分析 10 3.1需求分析 10 3.2可行性分析 10 3.2.1技术可行性:技术背景 10 3.2.2经济可行性 11 3.2.3操作可行性: 11 3.3性能分析 11 3.4系统操作流程 12 3.4.1管理员登录流程 12 3.4.2信息添加流程 12 3.4.3信息删除流程 13 第四章 系统设计与…...

Css Flex 弹性布局中的换行与溢出处理方法
Css Flex 弹性布局中的换行与溢出处理方法 CSS弹性布局(Flex)是CSS3中的一种新的布局方式,它能够帮助我们更加灵活地布局元素。在Flex弹性布局中,元素的布局仅依赖于父容器的设置,而不再需要复杂的相对或绝对定位。本…...
linux系统与应用
Windows中的硬盘和盘符的关系; 硬盘通常为一块到两块;数量与盘符没有直接关系;一块硬盘可以分为多个盘符,如c,d,e,f,g等;当然理论上也可以一块硬盘只有一个盘符;学习linux时,最好使用固态硬盘&a…...

MySQL的结构化语言 DDL DML DQL DCL
一、SQL结构化语言介绍 数据查询语言DQL:其语句称为“数据检索语言”,用以从库中获取数据,确定数据怎样在应用程序给出,保留select是dql(也是所有sql)用的最多的动词 数据操作语言DML:其语句包括动词insert…...

P5488 差分与前缀和
传送门:洛谷 前题提要:包含了简单的生成函数思想以及多项式乘法,是一道不可多得的多项式好题.故记录一下. 题意:给定一个长为 n 的序列 a,求出其 k 阶差分或前缀和。结果的每一项都需要对 1004535809取模。 对于差分和前缀和我们分开来讨论. 先讨论前缀和部分: …...

uboot启动流程-uboot内存分配
一. uboot启动流程 _main 函数中会调用 board_init_f 函数,本文继续简单分析一下 board_init_f 函数。 具体分析 board_init_f函数的第二部分:内存分配代码。 本文继上一篇文章的学习,地址如下: uboot启动流程-涉及board_init…...

LeetCode 面试题 08.02. 迷路的机器人
文章目录 一、题目二、C# 题解 一、题目 设想有个机器人坐在一个网格的左上角,网格 r 行 c 列。机器人只能向下或向右移动,但不能走到一些被禁止的网格(有障碍物)。设计一种算法,寻找机器人从左上角移动到右下角的路径…...
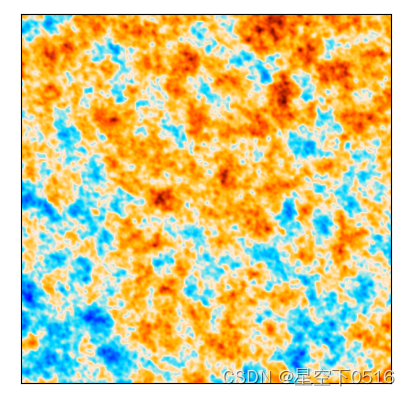
画CMB天图使用Planck配色方案
使用Planck的配色方案: 全天图: 或者方形图: 使用下面设置即可: import pspy, pixell from pspy.so_config import DEFAULT_DATA_DIR pixell.colorize.mpl_setdefault("planck")此方法不会改变matplotlib默认配色方案…...

成都瀚网科技有限公司:抖店精选联盟怎么用?
抖音精选联盟是抖音电商平台提供的一项服务,旨在为商家提供更多的推广机会和销售渠道。然而,很多人对于如何使用抖店精选联盟以及如何开通这项服务不太了解。本文将为您详细介绍抖店精选联盟的使用和激活流程。 第一节:如何使用抖店精选联盟 …...
)
第二章:最新版零基础学习 PYTHON 教程(第五节 - Python 输入/输出–如何在Python中打印而不换行?)
一般来说,从 C/C++ 切换到 Python 的人想知道如何在 python 中打印两个或多个变量或语句而不进入新行。由于Python print() 函数默认以换行符结尾。Python 有一个预定义的格式,如果你使用 print(a_variable) 那么它会自动转到下一行。 例子: # 输入:[csdn, csdnforcsdn] …...

C++实现集群聊天服务器
C实现集群聊天服务器 JSON Json是一种轻量级的数据交换模式(也叫做数据序列化方式)。Json采用完全独立于编程语言的文本格式来存储和表示数据。见解和清晰的层次结构使得Json称为理想的数据交换语言。易于阅读和编写。同时也易于支持机器解析和生成&am…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
