05. 机器学习入门 - 动态规划
文章目录
- 从一个案例开始
- 动态规划

Hi, 你好。我是茶桁。
咱们之前的课程就给大家讲了什么是人工智能,也说了每个人的定义都不太一样。关于人工智能的不同观点和方法,其实是一个很复杂的领域,我们无法用一个或者两个概念确定什么是人工智能,无法具体化。
我也是要给大家讲两个重要的概念,要成为一个良好的AI工作者,需要了解两个概念,一个是什么是优化问题,第二个呢就是什么是继续学习。
这一节开始,我们要开始进入机器学习的入门,这一部分只是机器学习的初级部分,我将其分成了三个部分,分别是:
- 如何衡量向量的相似性(metric for tensor)
- k-means算法进行聚类
- 线性回归与梯度下降
但是整体课程的排程并不是严格按照这三个部分来排的,所以大家能看到,我本篇课程的标题也并不是「如何衡量向量的相似性(metric for tensor)」。以上三个部分仅仅是我们当前这一部分会讲到的内容,但是也是拆散了放入课程中的。
从一个案例开始
那这节课最初,让我们从一个实际案例来引入,开始我们的深度学习初级之旅。
那要给大家讲的第一个问题,我们叫做optimization, 也叫做优化问题。那这里,我们拿一个实际的项目来。
我们所在的城市,可能很多人会经常看到运钞车。这个运钞车其实也是银行花钱雇的,运钞车其实也不是银行的。


每次要使用运钞车的时候是需需要花钱,还比较贵。这样就会带来一个结果,专门有人来策划运钞车的运行路径。为什么要策划计划运钞车的运行路径呢?因为如果我们有一台ATM机,ATM机满了,那么面对的一个问题就是别人存不进去钱了,
另外很重要一点是,如果一个ATM机满了而且没有把钱取出来,那这个钱就相当于是浪费了。加入一个ATM机能存一百万,那晚拿出来一天、两天,对银行来说损失就比较大。
还有一种情况就是这个ATM机空了,那客户去取钱的时候也取不到钱,也就起不到ATM机的作用。而银行对ATM机所在地的房租也就相当于白费了。
试想一下,如果同时有两张卡,一张农行卡,一张工行的卡,在农行准备想取钱的时候取不出来,就到工行去取了。而每次农行都取不出来,那之后就用工行用的多了。
在这样的情况下, 一个城市有很多个点, 就需要有很多个运钞车。
比方说在城市中有很多个ATM机的站点,现在我们有k个运钞车。
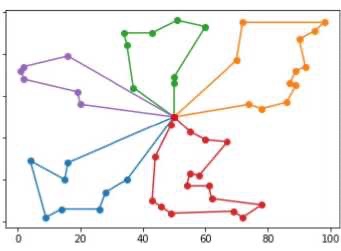
我们要策划一条线路,这个线路要使得所有的车,每个车每个点只走一遍,还要回到他出发的地方,而且这k个车运行的时间加起来是最小的。
那怎么样计划出这样一条路径呢?就这是一个非常典型的优化问题。对于此类的问题其实还有很多很相似的。
比如对于一家公司而言,手里的钱是有限的。如何把这些金额分配到不同的项目组中;

另外一个比方就是,对于一个公司来说如何选取合理的仓库的存货点,还有哪些仓库放哪些商品,能够让运输的车辆花的时间最少,能快速的去把这货物运输到不同的地方;这种物流问题是我最喜欢的问题之一。

或者我们制造一部手机,我们能花的钱就这么多,那怎么样能够在我们可以花的这个金额的范围内,如何选取最合理的元器件成本,让我们的手机达到最大的利润;

有很多约束条件,很多约束我们做决策的东西,总量不能大于多少。比方电的成本,水的成本等等,都要满足一定的关系才可以。这种东西我们就把它叫做约束条件。
要解决在约束条件下达成目标的这个问题,我们就把它叫做优化问题。
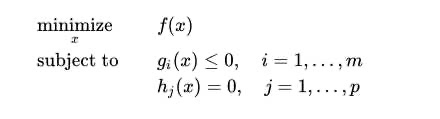
优化问题就是,我们可能会有不少的函数,这些函数去限定了之间的一种关系,也就是函数之间可能会有一些约束条件。比如图中的g_i(x)。
假设我们要造很多仓库,仓库加起来所花费的成本是什么样的, 花费的人力是什么样的。
最后要优化出来一个最小值就是我们的最小花费,或者所需要最少的时间。这种问题其实广泛存在于我们各个地方。
你点外卖每天在地图上做一个地图的规划,公司里做一笔投资,其实都是使用了类似这样的东西。
动态规划
我们要解决优化问题,其实有比较多的方法,今天来介绍最著名的一种,也是可以说是最重要的一种,动态规划的思想。
动态规划是一个什么样的情况?以这个问题引入一下。

想象一下有这么一个工厂,这个工厂是卖木头的,长度是一米的木头卖一块钱,长度2米的卖5块钱。
那么所以除非拿了一个一米的木头,否则不会有一个人像傻子一样说:把这个两米的木头截成两段。
图中我们可以看到,3米的就卖8块等等,到后面10米的卖30,11米的卖33。
那么现在你拿到了一个长度为8的一个木头,那你想想这个8米的木头是该直接卖,还是它切分掉去卖。切分掉去卖的话,如果用1和7,加起来就是18块钱,
2和6加起来就22块钱了,比8是不是就多了?
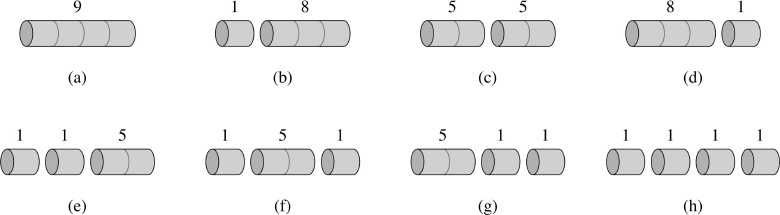
给你任意的一个长度n,然后我们要得出来这个n到底该怎么切分能够使得价格最大。怎么样能够让卖出去的价格最大。
思考一下咱们怎么解决这个问题。计算机有一个很很简单的方法,就是计算机有一个非常好的优点就是它可以做穷举。你可以让他去找什么,让他把所有东西全部都运行一遍就可以了。这是计算机的一个好处。
我们来思考一下咱们怎么样能够解决这个问题呢?
我们现在输入了一个长度是n的一个木头。它可以变成n和0,就是不切分。可以变成1和n-1, 变成2和n-2。一直截断到多少呢?可以变成n-n/2。
(0,n),(1, n-1),(2, n-2)…(n-n/2, n-n/2)
在这个情况下, 它分成1和n-1, n-1也面临了类似的问题。n-1是你直接返回n-1呢, 还是变成(1, n-2),变成(2, n-3)。对于2,其实也有也会面临这样一个问题,是返回2呢,还是(2-1, 2-1)。如果我们要遍历的话,遍历的就应该是一个树。把这个树里面所有情况都找一遍,然后返回那个最大值就可以了。
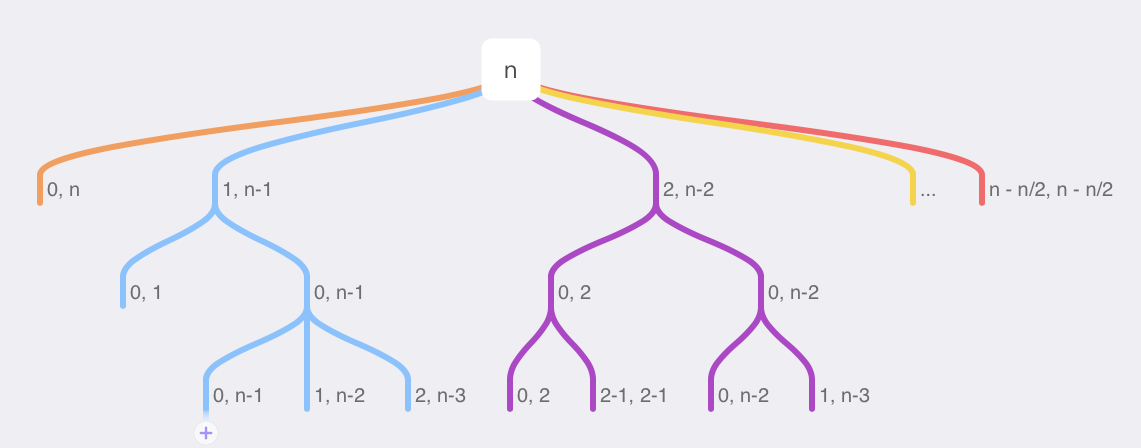
我们可以把所有的情况循环一遍,那我们现在来实现一下,你会发现其实一点也不难。
让我们来先定义一下所有的价格:
prices = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30 , 33]
我们要知道它的每一个商品直接的价钱,就是complete,我们来定义一个complete_price,
complete_price = { i+1: p for i, p in enumerate(prices)}
print(complete_price[9])---
24
那如果这个时候是30,就会出问题。
print(complete_price[30])---
KeyError: 30
遇到这种问题的时候不要非要去判断这个在不在里边,可以直接用detaultdict, 它是是一个带有默认值的Dictionary,如果这个值不存在的话,给它赋予一个默认值。
from collections import defaultdictcomplete_price = defaultdict(int)for i, p in enumerate(prices): complete_price[i+1] = pprint(complete_price[9])
print(complete_price[30])
这个时候如果是30, 它就有一个结果了。现在有了这样的一个基础数据,我们假如要写一个revenue,revenue就是营收,输入长度是n。
现在做一个很简单的方法:
def r(n):candidates = [complete_price[n]]
candidates等于价钱完全不切割是多少钱。然后我们写一个for循环:
for i in range(1, n):pass
接下来我们做个拆分,拆分左边就等于i, right就等于n-i:
left = i
right = n-i
这个时候整体的价格就等于complete_price[left], 再加完整的右边, complete_price[right]。
total_r = complete_price[left] + complete_price[right]
这里其实是有问题的, 如果我们在这里假设n现在是100, 假设运行到i是50, 那么complete_price[50] 其实是一个没有值的, 值是0。
就是数据里没有50的长度的价格,所以这个左边和右边其实是需要变成一个递归问题。
total_r = r(left) + r(right)
candidates.append(total_r)
现在写法写的稍微巧妙一些,这个就是我们刚才所说的遍历一遍,把所有的情况给拿出来,找到最大的返回出来。目前为止这个方法完整的代码如下:
def r(n):candidates = [complete_price[n]]for i in range(1, n):left = iright = n-itotal_r = r(left) + r(right)candidates.append(total_r)return max(candidates)这个时候我们来调用一下:
print(r(8))---
22
这个22是怎么来的呢? 我们来看一下上面这段代码, 首先8进方法之后, 第2行告诉我们8完全不切割的话是多少,并赋值给candidates。
紧接着把它变成了1和7,2和6,3和5,4和4这样的问题。
假如到6的时候,又会去求一下这个6。右边是要变成6,那么6最大应该是多少。
这个代码其实可以写成更加Python化的方式,我先写一遍上面的,是希望能让大家知道这个代码是怎么来的,现在让我们来用Python的方式来解决:
# 优化为Python向
def r(n):return max([complete_price[n]] + [r(i) + r(n-i) for i in range(1, n)])print(r(8))---
22
也就是,以上方法里定义的内容,完全可以压缩成一句话解决。你们可以仔细的研究一下这两段的相同点和差别。
现在的问题就是我们缺了一个记录他中间分割步骤的内容,这个也简单,我们稍微改变一下代码,将return改为赋值,然后给他加一个分割方法:
candidates = [(complete_price[n], (n, 0))] + [(r(i) + r(n-i), (i, n-i)) for i in range(1, n)]
其中我们添加了(n, 0), 还有(i,n-i)。
然后我们还要给他加上最优值:
optimal_price, split = max(candidates)
如果这其中你要是看不出逻辑过程,那你需要一些更多的练习。好好的再去回去看看我之前写的AI秘籍中的Python基础教程篇。
对于熟练的Python的工程师来说,应该熟悉这种方式才对。第一次咱们实现的方法,其实是C和Java的一种方法。如果是Python的话,你需要熟悉Python,直接会写成这个样子。
我们定义了一个candidates, 后面将风格方式定义进去并赋值给它。
然后我们使用optimal_price来接收它的最优价格。
接着,我们添加一个solution变量,solution是n的时候就找到了它的分割过程。
# 在方法外定义一个solution
solution = {}# 在方法内赋值solution[n]def r(n):...solution[n] = split
最后,我们还是将最优价格给返回出去。
return optimal_price
来看一下solution[8]
print(solution[8])---
(6, 2)
我们如果在这里debug一下这个solution,运行完之后solution如下:

是8的情况下变成6和2,现在就要看一下6的时候怎么切分?6的时候变成6和0。
好,现在我们来看一个更复杂的问题,我们将它变成33, 33你会发现他运行的时间很久。刚刚我们运行8,或者我们重新运行9的时候,速度都还可以,很快就能得到结果。但是运行33的时候就会非常的缓慢。知道这是为什么吗?
在这段代码中,现在有一个n,n接下来会拆分成了n-1个问题,其实是要进行n-1个循环。那每个n-1的循环里面又有两个调用了这个运算。所以在整个计算的次数的复杂性,对于一个n来说,它整个的运行时间应该是:2 * (n-1) * 2 * (n-2) * … = 2^n * n!,就等于2的n次方再乘上n的阶乘。
这样的话,结果就是它的运行时间会非常非常的久。那我们就需要对代码进行优化了。
如果现在仔细分析一下的话,会发现之所以运行的慢,问题在于很多重复的值其实被重复运算了。同样是n-3这个事,不仅在n-1向下分支中会计算一次,在其他的分支也会再计算很多次。有很多的值是被重复运算了。
为了解决重复运算的问题,我们可以做一个非常简单的方法。既然很多计算是重复的,那我定义一个变量去记录这些曾经计算过的,再遇到的时候就不要去计算不就完了:
cache = {}def r(n):if n in cache: return cache[n]...cache[n] = optimal_pricereturn optimal_priceprint(r(33))---
99
如果n在cache里面, 直接return cache[n], 如果它不在里边的话就往下继续运行,每次求完解的之后,我们让cache[n]等于optimal_price。这样就简单多了。
我们最后求了一下33,瞬间就得到了99的答案。
这个cache其实是很简单的一个东西,但是它其实是很重要的一种思想。在一九二几年、三几年的时候,当时有一个数学家叫Richard Bellman。Bellman发现在整个数学计算中有相当的一类问题,都牵扯到了一个相似的问题:over-lapping sub-problem,就是子问题的重复。
Bellman就提出来了一种方法,他就说我们解决这种问题其实有一个很简单的方法,用一张表格,不断地记录不断地查表,就是不断地写表查表。
就把值和结果都一一对应的写入表中,我们发现问题的时候,在这个表里面重新查一遍,看一下有没有这个值,存不存在。
当时Bellman把这种方法叫做Dynamic,不断地、持续地、变化的、动态的。programming在我们现在意思是编程,在一九二几、一九三几年的时候,是指把东西写到表格里以及从表格里面拿出来。
那为什么后来演化成编程的意思,因为早些时候,冯诺伊曼当年制作的那个机器写的是纸带,就是给你一个一个的纸带,这个纸带每一行会打八个洞,就是当时冯诺伊曼最早的计算机。这8个洞里边有一些是透光的,有一些是不透光的,其实就是一条一条计算机命令。
这其实也是一个写表读表的过程,后来programming就有了编程的意思。但是Bellman当年提出来的这个意思,Dandep programming就是不断地写表和查表。它针对的是所有一切有这个over-lapping sub-problem的问题,都可以用这种简单的方法,可以大幅度的减少计算性。
在很多地方学动态规划的时候,很多书上教动态规划的时候往往是直接给一个解法。不知道您有没有看过那些算法的书,在动态规划里往往会有一个表,这个表格很重要。
如果不用动态规划的话,这个问题也是能解决的。世界上几乎所有的这种优化问题不用动态规划都是可以解决的。但是理论上是要给你一个运算能力无限强,存储空间无限大的计算设备。
显然不太可能,所以我们就需要这样写到一个表格里边,记一个记录表格。这个就是我们动态规划的核心思想。
关于「动态规划的详解」之后有机会我去专门写个算法的相关课程,在这里就把动态规划的核心思想给大家介绍了。
我们现在来继续看代码,刚才我们算了一下33这个值,得到了99。但现在我们知道了能卖多少钱,但是我们还不知道到底怎么个拆分法。
要拆分的话我们就要把这个solution给它parse一下,再继续定义一个方法:
def parse_solution(n, cut_solution):left, right = cut_solution[n]if left == 0 or right == 0: return [left+right, ]else:return parse_solution(left, cut_solution) + parse_solution(right, cut_solution)print(r(18))
print(parse_solution(18, solution))---
52
[10, 6, 2]
我们看一下left和right,将分割分别传进来,那如果left和right是0的话,比如10, 写成(10, 0), 其实意思就是10就不用切分了,直接返回left和right就可以了。
那如果说它里边不是0,假如说是37,切分17和20,我们就要知道17该怎么分,20该怎么分。所以就返回:
return parse_solution(left, cut_solution) + parse_solution(right, cut_solution)
最后我们看到了18的切分结果,就被切分成[10, 6, 2]。
具体的切割过程也可以获得。
在Python里边呢这个是一个非常非常经典的动态规划问题。经过一个比较简单的方法,把重复问题给解决了。
再跟大家普及一个知识,在Python里面有一个好处就是它把很多常见的功能其实都已经想到,做了切分了。
比方说Python自带的库里面就有一个functools, 它有一个lru_cache,就是least recent used, 最近最少使用。
我们如果在直接写一个cache,它会存在一个问题。当n特别大的时候,那么cache的size也会变得特别的大。这个时候我们就需要一种机制,来让cache保留最需要保留的东西,保留那些最重要的东西,不要把所有的信息全部弄进去。
这个lru_cache帮我们实现了这个功能,它会把最近最少使用过的这些值删去, cache的这个size会保持在一个比较固定的范围内。
这个函数是一个装饰器,小伙伴们是否还记得我在Python课程中介绍过装饰器以及其使用?
我们来使用一下这个装饰器:
@lru_cache(maxsize=2**10)
这里定义了一下maxsize等于2的10次方,就是最多可以存2的10次方个值。
那这里和我们方法里的这一段内容其实是一摸一样:
if n in cache: return cache[n]
...
cache[n] = optimal_price
当我们调用这个函数的时候, 如果函数的参数曾经被计算过,那么就直接返回这个值。如果没有被计算过,就计算一遍,再把这个值写下来。
那我们使用了这个装饰器之后,我们对cache的使用的这两句代码就可以删掉了。
lru_cache的作用都懂了吧?以后遇到一个程序很慢的时候,就可以用它来做优化。
那其实今天这节课程把这个函数看懂,几乎所有的动态规划的问题的主体思路就都懂了。因为所有的动态规划的问题都包含了以下几个问题:
- 识别子问题 sub-problems dividing
- 识别子问题中的重叠特点 over-lapping sub-problem
- 存储子问题的答案 cache sub-solutions
- 合并问题答案 combine solutions
- 解析答案 parse solutions
这是所有的动态规划的特点,当你发现一个问题可以被分解成子问题,而且子问题有重复的时候,就可以用这种方法去优化它。
以后大家面试,大概率会遇到这种问题。只要按照这个方法来思考的话问题基本上就不大了。
但是动态规划其实也是有一个极限,曾经有一段时间人们以为动态规划可以解决很多问题,几乎可以解决所有常见的问题。但是后来人们发现,当限制条件特别多,或者问题已经复杂到非常难的去识别此问题了。可能它是包含了子问题的关系,但是因为这个问题太复杂了,所以我们没办法去把它分割出来,我们没有办法去识别它。
动态规划是一种思维方法,一种思维类型。比方计算机里面的图论问题,并不是只能把它变成图论问题,不用图论完全可以解决,但是不太好弄。
所以,动态规划其实也有它的局限性,人们为了解决更多问题就提出了更多的方法,其中一种方法就叫做机器学习。
好,我们下节课,就好好的来讲讲机器学习。本节课的最后,我将之前咱们写的那段代码完整版贴在这里:
from collections import defaultdict
from functools import lru_cacheprices = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30 , 33]
complete_price = defaultdict(int)for i, p in enumerate(prices): complete_price[i+1] = psolution = {}
cache = {}@lru_cache(maxsize=2**10)
def r(n):candidates = [(complete_price[n], (n, 0))] + [(r(i) + r(n-i), (i, n-i)) for i in range(1, n)]optimal_price, split = max(candidates)solution[n] = splitreturn optimal_pricedef parse_solution(n, cut_solution):left, right = cut_solution[n]if left == 0 or right == 0: return [left+right, ]else:return parse_solution(left, cut_solution) + parse_solution(right, cut_solution)print(r(18))
print(parse_solution(18, solution))
相关文章:

05. 机器学习入门 - 动态规划
文章目录 从一个案例开始动态规划 Hi, 你好。我是茶桁。 咱们之前的课程就给大家讲了什么是人工智能,也说了每个人的定义都不太一样。关于人工智能的不同观点和方法,其实是一个很复杂的领域,我们无法用一个或者两个概念确定什么是人工智能&a…...
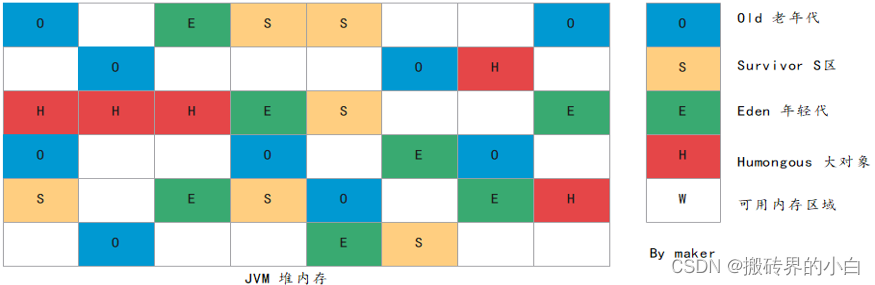
【JVM】第五篇 垃圾收集器G1和ZGC详解
导航 一. G1垃圾收集算法详解1. 大对象Humongous说明2. G1收集器执行一次GC运行的过程步骤3. G1垃圾收集分类4. G1垃圾收集器参数设置5. G1垃圾收集器的优化建议6. 适合使用G1垃圾收集器的场景?二. ZGC垃圾收集器详解1. NUMA与UMA2. 颜色指针3. ZGC的运作过程4. ZGC垃圾收集器…...

嵌入式Linux应用开发-基础知识-第十九章驱动程序基石⑤
嵌入式Linux应用开发-基础知识-第十九章驱动程序基石⑤ 第十九章 驱动程序基石⑤19.9 mmap19.9.1 内存映射现象与数据结构19.9.2 ARM架构内存映射简介19.9.2.1 一级页表映射过程19.9.2.2 二级页表映射过程 19.9.3 怎么给APP新建一块内存映射19.9.3.1 mmap调用过程19.9.3.2 cach…...

数据分析技能点-独立性检验拟合优度检验
在这个数据驱动的时代,数据分析已经成为了一个不可或缺的工具,无论是在商业决策、医疗研究还是日常生活中。然而数据分析并不仅仅是一堆数字和图表;它是一个需要严谨的科学方法和逻辑推理的过程。 本文将重点介绍两种广泛应用于数据分析的统计检验方法:独立性检验和拟合优…...
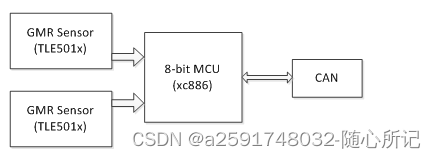
了解汽车ecu组成
常用ecu框架组成: BCM(body control module)-车身控制模块: 如英飞凌tc265芯片: 车身控制单元(BCM)适合应用于12V和24V两种电压工作环境,可用于轿车、大客车和商用车的车身控制。输入模块通过采集电路采集各路开关量和…...

用AI原生向量数据库Milvus Cloud 搭建一个 AI 聊天机器人
搭建聊天机器人 一切准备就绪后,就可以搭建聊天机器人了。 文档存储 机器人需要存储文档块以及使用 Towhee 提取出的文档块向量。在这个步骤中,我们需要用到 Milvus。 安装轻量版 Milvus Lite,使用以下命令运行 Milvus 服务器: (chatbot_venv) [egoebelbecker@ares milvus_…...

【OpenCV-Torch-dlib-ubuntu】Vm虚拟机linux环境摄像头调用方法与dilb模型探究
前言 随着金秋时节的来临,国庆和中秋的双重喜庆汇聚成一片温暖的节日氛围。在这个美好的时刻,我们有幸共同迎来一次长达8天的假期,为心灵充电,为身体放松,为未来充实自己。今年的国庆不仅仅是家国团聚的时刻ÿ…...
详解观察者模式)
(二)详解观察者模式
一.使用场景 当我们需要一个类,在他的内部元素发生变化的时候可以主动通知其他类的时候,同时要保持良好的可拓展性,可以采用观察者模式。 二.核心 观察者模式出版者订阅者 我们拥有一个主题对象,和一些其他对象,包…...

嵌入式Linux应用开发-基础知识-第十九章驱动程序基石④
嵌入式Linux应用开发-基础知识-第十九章驱动程序基石④ 第十九章 驱动程序基石④19.7 工作队列19.7.1 内核函数19.7.1.1 定义 work19.7.1.2 使用 work:schedule_work19.7.1.3 其他函数 19.7.2 编程、上机19.7.3 内部机制19.7.3.1 Linux 2.x的工作队列创建过程19.7.3…...
2023 彩虹全新 SUP 模板,卡卡云模板修复版
2023 彩虹全新 SUP 模板,卡卡云模板,首页美化,登陆页美化,修复了 PC 端购物车页面显示不正常的问题。 使用教程 将这俩个数据库文件导入数据库; 其他的直接导入网站根目录覆盖就好; 若首页显示不正常&a…...

【AI视野·今日NLP 自然语言处理论文速览 第四十一期】Tue, 26 Sep 2023
AI视野今日CS.NLP 自然语言处理论文速览 Tue, 26 Sep 2023 Totally 75 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Physics of Language Models: Part 3.1, Knowledge Storage and Extraction Authors Zeyuan Allen Zhu, Yuanz…...
【iptables 实战】05 iptables设置网络转发实验
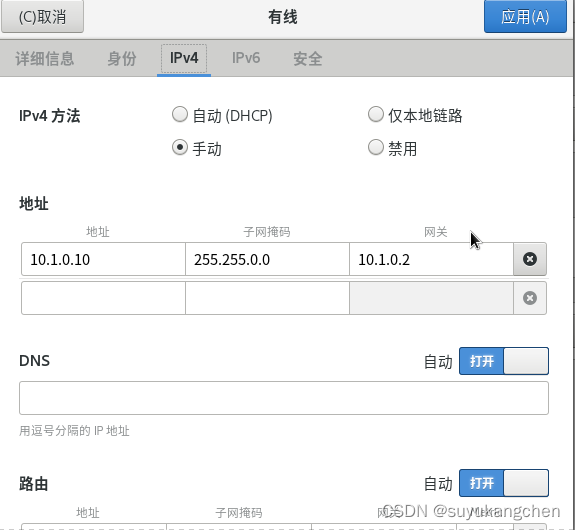
一、网络架构 实验效果,通过机器B的转发功能,将机器A的报文转发到机器C 本实验准备三台机器分别配置如下网络 机器A ip:192.168.56.104 机器C ip:10.1.0.10 机器B 两张网卡,分别的ip是192.168.56.106和10.1.0.11 如图所示 如下图所示 二、…...

pygame - 贪吃蛇小游戏
蛇每吃掉一个身体块,蛇身就增加一个长度。为了统一计算,界面的尺寸和游戏元素的位置都是身体块长度的倍数 1. 上下左右方向键(或者ASDW键)控制蛇的移动方向 2. 空格键暂停和继续蛇的身体图片文件,复制到项目的asset\im…...
基于 QT 实现 Task Timer,高效利用时间
一、开发环境 Ubuntu 20.04 QT6.0 二、新建 Qt Wigets Application 这里的基类选择 Wigets, pro 配置文件添加 sql 模块,需要用到 sqlite, QT sql 三、添加数据库连接头文件 // connection.h #ifndef CONNECTION_H #define CONNECTION_…...

图像处理与计算机视觉--第五章-图像分割-霍夫变换
文章目录 1.霍夫变换(Hough Transform)原理介绍2.霍夫变换(Hough Transform)算法流程3.霍夫变换(Hough Transform)算法代码4.霍夫变换(Hough Transform)算法效果 1.霍夫变换(Hough Transform)原理介绍 Hough Transform是一种常用的计算机视觉图形检验方法,霍夫变换一…...

linux下文件操作命令
title: linux下文件操作命令 createTime: 2020-10-29 18:05:52 updateTime: 2020-10-29 18:05:52 categories: linux tags: Linux下文件操作命令 tar命令 使用tar命令一般打包分为两种*.tar ,*.tar.gz 相信大家也使用过tar -zcvf test.tar test/tar -zcvf test.tar.gz test/…...

Golang语法、技巧和窍门
Golang简介 命令式语言静态类型语法标记类似于C(但括号较少且没有分号),结构类似Oberon-2编译为本机代码(没有JVM)没有类,但有带有方法的结构接口没有实现继承。不过有type嵌入。函数是一等公民函数可以返…...
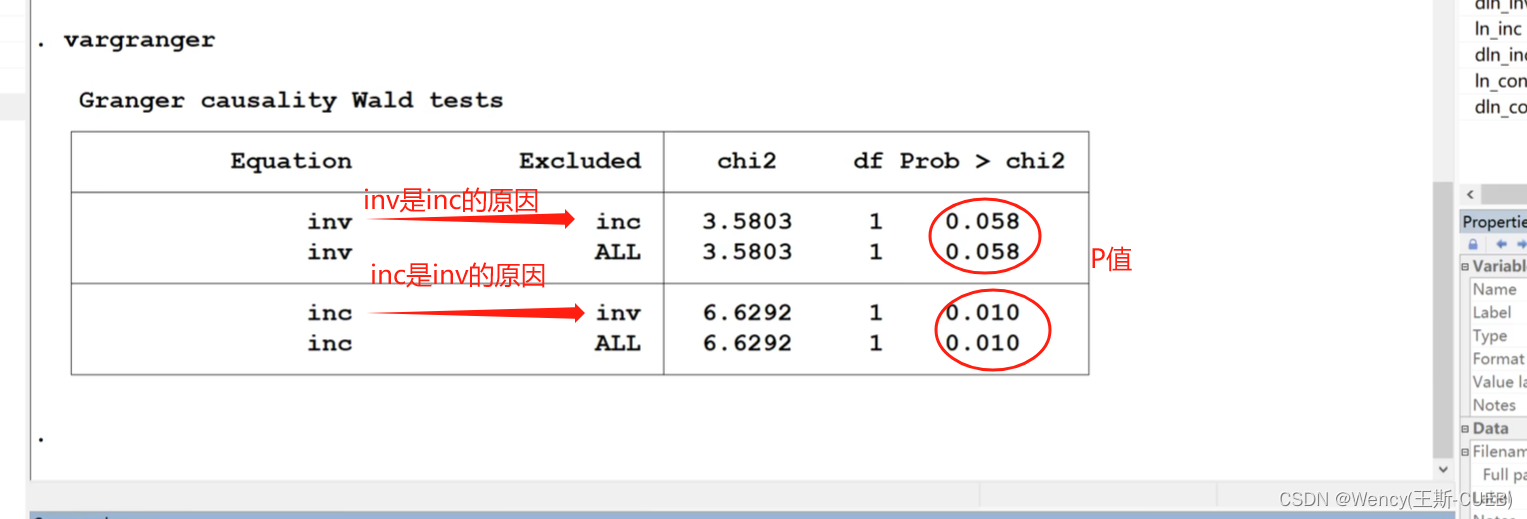
Grander因果检验(格兰杰)原理+操作+解释
笔记来源: 1.【传送门】 2.【传送门】 前沿原理介绍 Grander因果检验是一种分析时间序列数据因果关系的方法。 基本思想在于,在控制Y的滞后项 (过去值) 的情况下,如果X的滞后项仍然有助于解释Y的当期值的变动,则认为 X对 Y产生…...
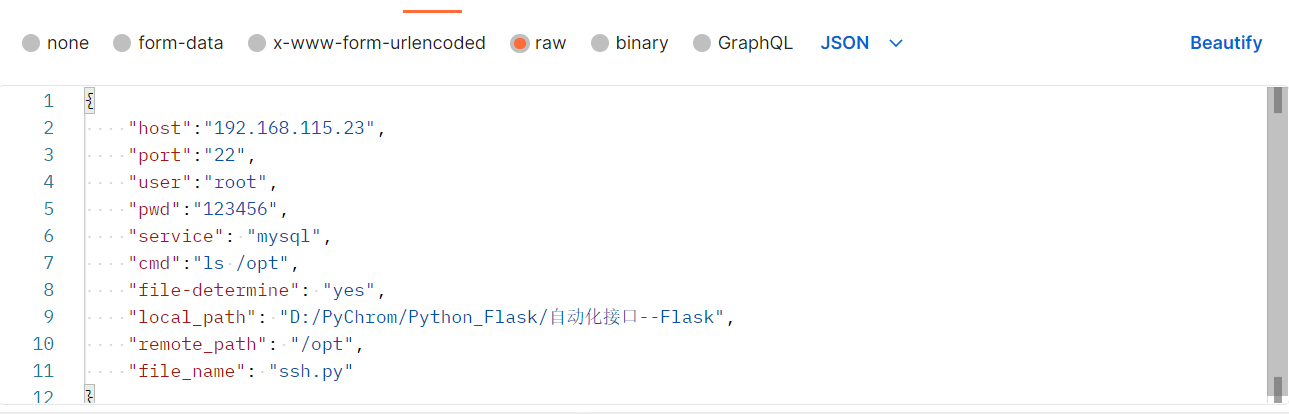
Python-Flask:编写自动化连接demo脚本:v1.0.0
主函数: # _*_ Coding : UTF-8 _*_ # Time : 13:14 # Author : YYZ # File : Flask # Project : Python_Project_爬虫 import jsonfrom flask import Flask,request,jsonify import sshapi Flask(__name__)# methods: 指定请求方式 接口解析参数host host_info[…...
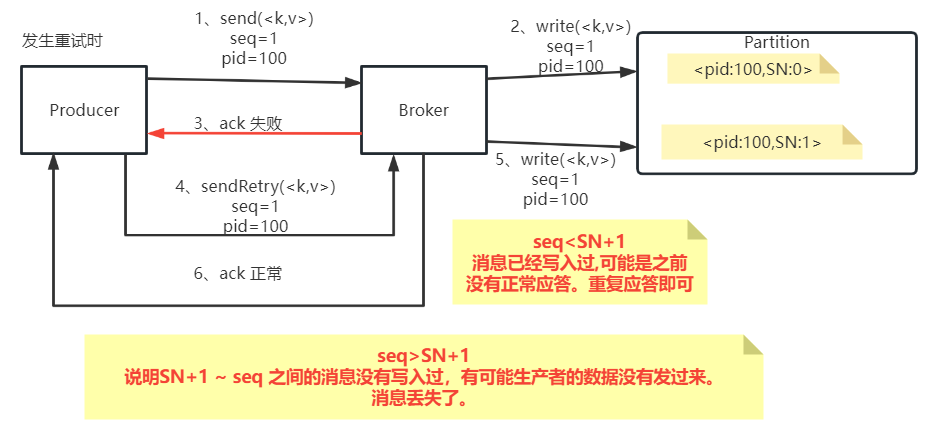
kafka客户端应用参数详解
一、基本客户端收发消息 Kafka提供了非常简单的客户端API。只需要引入一个Maven依赖即可: <dependency><groupId>org.apache.kafka</groupId><artifactId>kafka_2.13</artifactId><version>3.4.0</version></depend…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
