机器人中的数值优化(二十)——函数的光滑化技巧
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
三十二、函数的光滑化技巧
1、Inf convolution 卷积操作
Inf convolution 卷积操作适应于凸函数,Inf convolution 卷积操作的目标是把不光滑的凸函数进行光滑近似,并使得光滑近似后的函数于原函数尽量吻合
对于两个凸函数 f 1 f_1 f1、 f 2 f_2 f2,它们之间的Inf convolution 卷积操作记为 f 1 □ f 2 f_{1}□ f_{2} f1□f2,即找一个 u 1 u_1 u1和 u 2 u_2 u2,满足 u 1 u_1 u1+ u 2 u_2 u2= x x x的条件下,使得 f 1 ( u 1 ) + f 2 ( u 2 ) f_{1}(u_{1})+f_{2}(u_{2}) f1(u1)+f2(u2)最大或最小,如下面的第一个表达式所示,由于满足 u 1 u_1 u1+ u 2 u_2 u2= x x x,因此可消去一个u进行简化,简化后的表达式如下面第二个式子所示:
( f 1 □ f 2 ) ( x ) = inf ( u 1 , u 2 ) ∈ R d × R d { f 1 ( u 1 ) + f 2 ( u 2 ) : u 1 + u 2 = x } ( f 1 □ f 2 ) ( x ) = inf u ∈ R d { f 1 ( u ) + f 2 ( x − u ) } \begin{aligned}(f_1□ f_2)(x)&=\inf_{(u_1,u_2)\in\mathbb{R}^d\times\mathbb{R}^d}\{f_1(u_1)+f_2(u_2):u_1+u_2=x\}\\(f_1□ f_2)(x)&=\inf_{u\in\mathbb{R}^d}\{f_1(u)+f_2(x-u)\}\end{aligned} (f1□f2)(x)(f1□f2)(x)=(u1,u2)∈Rd×Rdinf{f1(u1)+f2(u2):u1+u2=x}=u∈Rdinf{f1(u)+f2(x−u)}
Inf convolution 卷积具有对称性,即 f 1 □ f 2 = f 2 □ f 1 f_1□ f_2=f_2□ f_1 f1□f2=f2□f1
Inf convolution 卷积的几何解释如下图所示,假设我们考虑两个凸函数,一个是常见的绝对值函数 f ( x ) = ∣ x ∣ \color{red}{f(x)=|x|} f(x)=∣x∣,另一个是二次函数 g ( x ) = 1 2 x 2 g(x)=\frac12x^2 g(x)=21x2,如下面的第一幅图所示,对这两个函数进行Inf convolution 卷积操作,即将光滑的函数 g ( x ) = 1 2 x 2 g(x)=\frac12x^2 g(x)=21x2的原点不断地在绝对值函数 f ( x ) = ∣ x ∣ \color{red}{f(x)=|x|} f(x)=∣x∣上进行移动,依次得到下面的第二幅图和第三幅图,最终得到包络即f函数与g函数的Inf convolution 卷积操作。

如果min可以取到的话, e p i ( f □ g ) = e p i ( f ) + e p i ( g ) epi(f□g)=epi(f)+epi(g) epi(f□g)=epi(f)+epi(g)
Inf convolution 卷积操作的原理其实就是拿光滑凸函数的轮廓去把不光滑的地方利用包络给它磨圆
2、Moreau 包络
Moreau envelope是Inf convolution 卷积操作的一个特例,即将被卷积函数更改为一个二次函数或者说范数的平方,如下式所示:
γ f : = f □ ( 1 2 γ ∥ ⋅ ∥ 2 ) ^\gamma f:=f\Box\left(\frac{1}{2\gamma}\|\cdot\|^2\right) γf:=f□(2γ1∥⋅∥2)
其具体表达式如下式所示:
γ f ( x ) : = inf u ∈ R d { f ( u ) + 1 2 γ ∥ x − u ∥ 2 } ^\gamma f(x):=\inf_{u\in\mathbb{R}^d}\{f(u)+\frac{1}{2\gamma}\left\|x-u\right\|^2\} γf(x):=u∈Rdinf{f(u)+2γ1∥x−u∥2}
当一个函数时封闭的凸函数时,inf一定可以取到最小值, γ \gamma γ具有平滑参数的作用, γ \gamma γ越小,平滑后的函数与原函数越接近。

下面来看一个Pinball函数的示例,Pinball函数的定义如下
ℓ s 1 , s 2 ( x ) = { s 1 x if x ≤ 0 s 2 x if x ≥ 0 \ell_{s_1,s_2}(x)=\begin{cases}s_1x&\text{if}x\le0\\s_2x&\text{if}x\ge0\end{cases} ℓs1,s2(x)={s1xs2xifx≤0ifx≥0
其中, s 1 ≤ 0 ≤ s 2 s_1\leq0\leq s_2 s1≤0≤s2,Pinball函数的Moreau 包络函数如下所示
γ f ( x ) = ( f □ g ) ( x ) = = { s 1 x − γ s 1 2 2 , if x < s 1 1 2 γ x 2 , if x ∈ [ γ s 1 , γ s 2 ] s 2 x − γ s 2 2 2 , if x > s 2 \gamma f(x)=(f\Box g)(x)==\quad\begin{cases}s_1x-\gamma\frac{s_1^2}{2},&\text{if }x<s_1\\\frac{1}{2\gamma}x^2,&\text{if }x\in[\gamma s_1,\gamma s_2]\\s_2x-\gamma\frac{s_2^2}{2},&\text{if }x>s_2\end{cases} γf(x)=(f□g)(x)==⎩ ⎨ ⎧s1x−γ2s12,2γ1x2,s2x−γ2s22,if x<s1if x∈[γs1,γs2]if x>s2
一个经典的例子是Huber函数 ℓ − 1 , 1 \ell_{-1,1} ℓ−1,1,即 s 1 s_1 s1取-1, s 2 s_2 s2取1

相关证明如下:

当我们不断地把 γ \gamma γ值减小,平滑后的函数与原函数也更加接近,包络的下边缘也会越来越尖,如下图所示:

Moreau 包络具有一个良好的性质,即一个函数与它的Moreau 包络函数的最小值相同,即
∀ γ > 0 , inf x ( ( γ f ) ( x ) ) = inf x f ( x ) \forall\gamma>0,\quad\inf_x\left((^\gamma f)(x)\right)=\inf_xf(x) ∀γ>0,xinf((γf)(x))=xinff(x)
证明过程如下:
inf x ( ( γ f ) ( x ) ) = inf x inf y { f ( y ) + 1 2 γ ∥ x − y ∥ 2 } = inf y inf x { f ( y ) + 1 2 γ ∥ x − y ∥ 2 } = inf y f ( y ) \begin{aligned} \operatorname*{inf}_{x}\left((^{\gamma}f)(x)\right)& =\inf_x\inf_y\left\{f(y)+\frac1{2\gamma}\left\|x-y\right\|^2\right\} \\ &=\inf_y\inf_x\left\{f(y)+\frac{1}{2\gamma}\left\|x-y\right\|^2\right\} \\ &=\inf_{y}f(y) \end{aligned} xinf((γf)(x))=xinfyinf{f(y)+2γ1∥x−y∥2}=yinfxinf{f(y)+2γ1∥x−y∥2}=yinff(y)

总结一下,用Inf convolution 卷积操作可以对一个不光滑的凸函数进行平滑,平滑后的函数与原函数具有同样的最小值,给一个光滑因子 γ \gamma γ用来调节光滑程度,我们把不光滑的凸函数 f f f的光滑近似记作 ω γ f _{\omega}^{\gamma}f ωγf, ω \omega ω是我们用来光滑 f f f的被卷积的函数, ω \omega ω取 1 2 ∥ ⋅ ∥ 2 \frac{1}{2}\|\cdot\|^2 21∥⋅∥2时,就是Moreau 包络

假设,我们用 g ( x ) = 1 2 x 2 + 1 2 g(x)=\frac12x^2+\frac12 g(x)=21x2+21来作为被卷积的函数,把 g ( x ) g(x) g(x)的原点挪动一遍后,形成的包络如下图所示,我们可以改变 g ( x ) g(x) g(x)来获得不同的效果。

Inf-conv卷积是平滑凸函数的一种常用方法。它可以处理Moreau 包络或者Nesterov 平滑无法处理的问题。

3、Mollifier-Conv
Mollifier卷积是比Inf-conv卷积更一般化的卷积,举一个例子,对于如式所示的函数,它是通过 e − 1 1 − x 2 e^\frac{-1}{1-x^2} e1−x2−1变化而来的,除以其自身的积分相当于进行了缩放操作,这样一个凸起的或者说隆起的函数就称为Mollifier
φ ( x ) = { e − 1 / ( 1 − x 2 ) ∫ − 1 1 e − 1 / ( 1 − s 2 ) d s i f ∣ x ∣ < 1 0 i f ∣ x ∣ ≥ 1 \varphi(x)=\begin{cases}\frac{e^{-1/(1-x^2)}}{\int_{-1}^1e^{-1/(1-s^2)}\mathrm{d}s}&\mathrm{~if~}|x|<1\\0&\mathrm{~if~}|x|\geq1&\end{cases} φ(x)=⎩ ⎨ ⎧∫−11e−1/(1−s2)dse−1/(1−x2)0 if ∣x∣<1 if ∣x∣≥1

更一般的,取 φ ϵ ( x ) : = 1 ϵ φ ( x ϵ ) \varphi_\epsilon(x):=\frac1\epsilon\varphi(\frac x\epsilon) φϵ(x):=ϵ1φ(ϵx),将该函数与下面右图中红色曲线所示的函数进行卷积 f ϵ ( x ) : = ∫ − ∞ + ∞ f ( x + z ) φ ϵ ( z ) d z f_\epsilon(x):=\int_{-\infty}^{+\infty}f(x+z)\varphi_\epsilon(z)dz fϵ(x):=∫−∞+∞f(x+z)φϵ(z)dz,得到了下面右图中的蓝色曲线,其中 ϵ \epsilon ϵ用于调节光滑效果, ϵ \epsilon ϵ越小光滑效果越差,越接近于原函数。

下图中给出了一个二维的例子,在一维的基础上进行了推广
φ ( x ) = { e − 1 / ( 1 − ∥ x ∥ 2 ) ∫ R n e − 1 / ( 1 − ∥ s ∥ 2 ) d s i f ∥ x ∥ < 1 0 i f ∥ x ∥ ≥ 1 \varphi(x)=\begin{cases}\frac{e^{-1/(1-\|x\|^2)}}{\int_{\mathbb{R}^n}e^{-1/(1-\|s\|^2)}\mathrm{d}s}&\mathrm{~if~}\|x\|<1\\0&\mathrm{~if~}\|x\|\geq1&\end{cases} φ(x)=⎩ ⎨ ⎧∫Rne−1/(1−∥s∥2)dse−1/(1−∥x∥2)0 if ∥x∥<1 if ∥x∥≥1

φ ϵ ( x ) : = 1 ϵ n φ ( x ϵ ) f ϵ ( x ) : = ∫ − ∞ + ∞ f ( x + z ) φ ϵ ( z ) d z \begin{gathered}\varphi_\epsilon(x):=\frac1{\epsilon^n}\varphi\Big(\frac x\epsilon\Big)\\\\f_\epsilon(x):=\int_{-\infty}^{+\infty}f(x+z)\varphi_\epsilon(z)dz\end{gathered} φϵ(x):=ϵn1φ(ϵx)fϵ(x):=∫−∞+∞f(x+z)φϵ(z)dz

Mollifier的具体定义如下所示,其满足积分为1,且当 ϵ \epsilon ϵ趋于0的时候, φ ( x ) \varphi(x) φ(x)趋于冲激函数 δ ( x ) \delta(x) δ(x),只要满足这两个条件都可以称为Mollifier
∫ R n φ ( x ) d x = 1 lim ϵ → 0 φ ϵ ( x ) = lim ϵ → 0 ϵ − n φ ( x / ϵ ) = δ ( x ) \begin{aligned}&\int_{\mathbb{R}^n}\varphi(x)\mathrm{d}x=1\\&\lim_{\epsilon\to0}\varphi_\epsilon(x)=\lim_{\epsilon\to0}\epsilon^{-n}\varphi(x/\epsilon)=\delta(x)\end{aligned} ∫Rnφ(x)dx=1ϵ→0limφϵ(x)=ϵ→0limϵ−nφ(x/ϵ)=δ(x)
下面进行简单的推导,为什么使用Mollifier函数进行卷积操作,可对原函数进行平滑处理
d d x f ϵ ( x ) = d d x ∫ f ( x + z ) φ ϵ ( z ) d z = d d x ∫ f ( y ) φ ϵ ( y − x ) d y = ∫ f ( y ) ( d d x φ ϵ ( y − x ) ) d y \begin{aligned} \frac d{dx}f_\epsilon(x)& =\frac d{dx}\int f(x+z)\varphi_\epsilon(z)\mathrm{d}z \\ &=\frac d{dx}\int f(y)\varphi_\epsilon(y-x)dy \\ &=\int f(y)\left(\frac d{dx}\varphi_\epsilon(y-x)\right)dy \end{aligned} dxdfϵ(x)=dxd∫f(x+z)φϵ(z)dz=dxd∫f(y)φϵ(y−x)dy=∫f(y)(dxdφϵ(y−x))dy
即若Mollifier函数是处处连续可微的,则对某个函数进行Mollifier卷积操作后得到的函数也是处处连续可微的,
在下面的例子中,Mollifier函数取为 φ ( x ) = 1 e x + e − x + 2 \varphi(x)=\frac1{e^x+e^{-x}+2} φ(x)=ex+e−x+21,原函数为 f ( x ) = max ( x , 0 ) f(x)=\max(x,0) f(x)=max(x,0),则进行Mollifier卷积后的函数变为下式:
f ϵ ( x ) = ∫ − ∞ + ∞ max ( x + z , 0 ) φ ϵ ( z ) d x = ϵ ln ( 1 + e x / ϵ ) f_\epsilon(x)=\int_{-\infty}^{+\infty}\max(x+z,0)\varphi_\epsilon(z)\mathrm{d}x=\epsilon\ln(1+e^{x/\epsilon}) fϵ(x)=∫−∞+∞max(x+z,0)φϵ(z)dx=ϵln(1+ex/ϵ)
Mollifier卷积后的效果如下面的右图所示:

我们知道 max ( x 1 , x 2 ) \max(x_1,x_2) max(x1,x2)等价于 x 1 + max ( x 2 − x 1 , 0 ) x_1+\max(x_2-x_1,0) x1+max(x2−x1,0),代入上面的表达式,我们可以进一步得到原函数为 max ( x 1 , x 2 ) \max(x_1,x_2) max(x1,x2)时,Mollifier卷积后的结果为 ϵ ln ( e x 1 / ϵ + e x 2 / ϵ ) \epsilon\ln(e^{x_1/\epsilon}+e^{x_2/\epsilon}) ϵln(ex1/ϵ+ex2/ϵ),同理可推广到多个值取max的情况,如下所示:
max ( x 1 , x 2 ) = x 1 + max ( x 2 − x 1 , 0 ) ⟷ x 1 + f ϵ ( x 2 − x 1 ) = ϵ ln ( e x 1 / ϵ + e x 2 / ϵ ) max ( x 1 , … , x n − 1 , x n ) = max ( x n , max ( x 1 , … , x n − 1 ) ) ⟷ ϵ ln ∑ i = 1 n e x i / ϵ l o g ⋅ s u m ⋅ e α p \begin{aligned}\max(x_1,x_2)&=x_1+\max(x_2-x_1,0)\quad\longleftrightarrow\quad&x_1+f_\epsilon(x_2-x_1)=\epsilon\ln(e^{x_1/\epsilon}+e^{x_2/\epsilon})\\\max(x_1,\ldots,x_{n-1},x_n)&=\max(x_n,\max(x_1,\ldots,x_{n-1}))\quad\longleftrightarrow\quad&\epsilon\ln\sum_{i=1}^ne^{x_i/\epsilon\quad\mathsf{log}\cdot\mathsf{sum}\cdot\mathsf{e}\alpha\mathbf{p}}\end{aligned} max(x1,x2)max(x1,…,xn−1,xn)=x1+max(x2−x1,0)⟷=max(xn,max(x1,…,xn−1))⟷x1+fϵ(x2−x1)=ϵln(ex1/ϵ+ex2/ϵ)ϵlni=1∑nexi/ϵlog⋅sum⋅eαp

–
当 ϵ \epsilon ϵ取1时, max { x 1 , … , x k } \max\{x_1,\ldots,x_k\} max{x1,…,xk}函数经过Mollifier卷积处理后的示意图如下所示:

所以, f ( x ) : = log ( ∑ k = 1 n exp x k ) f(x):=\log\left(\sum_{k=1}^n\exp x_k\right) f(x):=log(∑k=1nexpxk)可以被视为光滑的max函数的替代品,在工程中很常用。
若我们将Mollifier函数更改为 φ ( x ) = 2 ( x 2 + 4 ) 3 / 2 \color{red}{\varphi(x)=\frac2{(x^2+4)^{3/2}}} φ(x)=(x2+4)3/22,原函数为 f ( x ) = max ( x , 0 ) f(x)=\max(x,0) f(x)=max(x,0),则进行Mollifier卷积后的函数变为下式,这个函数也被称为CHKS函数,常用作光滑化的max 函数来对max函数进行替代。
f ϵ ( x ) = ∫ − ∞ + ∞ max ( x + z , 0 ) φ ϵ ( z ) d x = x + x 2 + 4 ϵ 2 2 f_\epsilon(x)=\int_{-\infty}^{+\infty}\max(x+z,0)\varphi_\epsilon(z)\mathrm{d}x=\frac{x+\sqrt{x^2+4\epsilon^2}}2 fϵ(x)=∫−∞+∞max(x+z,0)φϵ(z)dx=2x+x2+4ϵ2

下面给出了一个Weierstrass变换的例子,Weierstrass变换是连续版本的高斯模糊,他也可以得到光滑的函数

下面给出了一个采用分段光滑的例子
F μ ( x ) = { 0 i f x ≤ 0 ( μ − x / 2 ) ( x / μ ) 3 i f 0 < x < μ x − μ / 2 i f x ≥ μ F_\mu(x)=\begin{cases}0&\mathrm{~if~}x\leq0\\(\mu-x/2)(x/\mu)^3&\mathrm{~if~}0<x<\mu\\x-\mu/2&\mathrm{~if~}x\geq\mu&\end{cases} Fμ(x)=⎩ ⎨ ⎧0(μ−x/2)(x/μ)3x−μ/2 if x≤0 if 0<x<μ if x≥μ

参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化
相关文章:

机器人中的数值优化(二十)——函数的光滑化技巧
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

搭建全连接网络进行分类(糖尿病为例)
拿来练手,大神请绕道。 1.网上的代码大多都写在一个函数里,但是其实很多好论文都是把网络,数据训练等分开写的。 2.分开写就是有一个需要注意的事情,就是要import 要用到的文件中的模型或者变量等。 3.全连接的回归也写了&#…...
【小沐学前端】Node.js实现基于Protobuf协议的UDP通信(UDP/TCP)
文章目录 1、简介1.1 node1.2 Protobuf 2、下载和安装2.1 node2.2 Protobuf2.2.1 安装2.2.2 工具 3、node 代码示例3.1 HTTP3.2 UDP单播3.4 UDP广播 4、Protobuf 代码示例4.1 例子: awesome.proto4.1.1 加载.proto文件方式4.1.2 加载.json文件方式4.1.3 加载.js文件方式 4.2 例…...

Verasity Tokenomics — 社区讨论总结与下一步计划
Verasity 代币经济学的社区讨论已结束。 本次讨论从 8 月 4 日持续到 9 月 29 日,是区块链领域规模最大的讨论之一,超过 500,000 名 VRA 持有者和社区成员参与讨论,并收到了数千份回复。 首先,我们要感谢所有参与讨论并提出详细建…...

JUC第十三讲:JUC锁: ReentrantLock详解
JUC第十三讲:JUC锁: ReentrantLock详解 本文是JUC第十三讲,JUC锁:ReentrantLock详解。可重入锁 ReentrantLock 的底层是通过 AbstractQueuedSynchronizer 实现,所以先要学习上一章节 AbstractQueuedSynchronizer 详解。 文章目录 …...

WSL2安装历程
WLS2安装 1、系统检查 安装WSL2必须运行 Windows 10 版本 2004 及更高版本(内部版本 19041 及更高版本)或 Windows 11。 查看 Windows 版本及内部版本号,选择 Win R,然后键入winver。 2、家庭版升级企业版 下载HEU_KMS_Activ…...
Ubuntu20配置Mysql常用操作
文章目录 版权声明ubuntu更换软件源Ubuntu设置静态ipUbuntu防火墙ubuntu安装ssh服务Ubuntu安装vmtoolsUbuntu安装mysql5.7Ubuntu安装mysql8.0Ubuntu卸载mysql 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明,所有版权属于黑马程…...

【解决方案】‘create’ is not a member of ‘cv::aruco::DetectorParameters’
‘create’ is not a member of ‘cv::aruco::DetectorParameters’ 在构建AruCo标定板标定位姿代码的过程中,发现代码中认为create并不是aruco::DetectorParameters的成员函数,这是因为在4.7.0及以上的OpenCV版本中,对ArUco的代码做调整&…...
)
门牌制作(蓝桥杯)
门牌制作 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 小蓝要为一条街的住户制作门牌号。 这条街一共有 2020 位住户,门牌号从 1 到 2020 编号。 小蓝制作门牌的方法是先制作 0 到 9 这几个数字字…...
支付宝支付模块开发
生成二维码 使用Hutool工具类生成二维码 引入对应的依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.7.5</version> </dependency><dependency><groupId>com.go…...

12、Kubernetes中KubeProxy实现之iptables和ipvs
目录 一、概述 二、iptables 代理模式 三、iptables案例分析 四、ipvs案例分析 一、概述 iptables和ipvs其实都是依赖的一个共同的Linux内核模块:Netfilter。Netfilter是Linux 2.4.x引入的一个子系统,它作为一个通用的、抽象的框架,提供…...

从0开始python学习-29.selenium 通过cookie信息进行登录
1. 手动输入cookie信息保持登录状态 url https://test.com/login driver.get(url) # 手动将cookie信息写入(有多个的情况需要分开写入)--弊端为需要每次都手动输入,很麻烦不适用 driver.add_cookie({"name": "SIAM_IMAGE_…...

CentOS安装OpenNebula(二)
被控端部署: 先要配置好yum源: [rootmaster yum.repos.d]# vim opennebula.repo[rootmaster yum.repos.d]# cat opennebula.repo [opennebula] nameopennebula baseurlhttps://downloads.opennebula.org/repo/5.6/CentOS/7/x86_64 enabled1 gpgkeyhttps…...

力扣第239题 c++滑动窗口经典题 单调队列
题目 239. 滑动窗口最大值 困难 提示 队列 数组 滑动窗口 单调队列 堆(优先队列) 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的…...

华为云云耀云服务器L实例评测|华为云云耀云服务器docker部署srs,可使用HLS协议
华为云云耀云服务器L实例评测|华为云云耀云服务器docker部署srs,可使用HLS协议 什么是华为云云耀云L实例 云耀云服务器L实例,面向初创企业和开发者打造的全新轻量应用云服务器。提供丰富严选的应用镜像,实现应用一键部署&#x…...
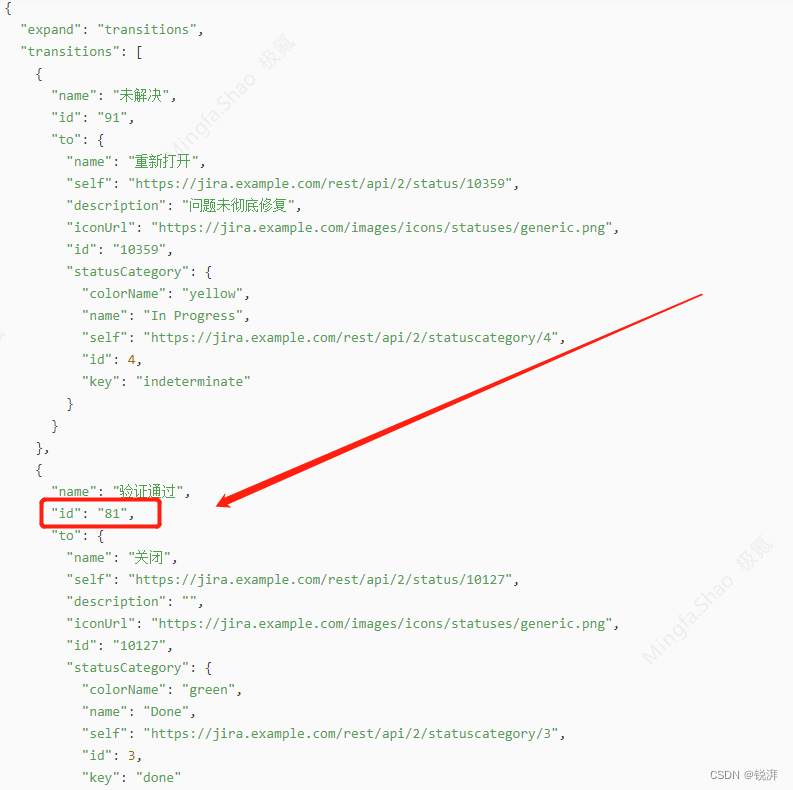
jira流转issue条目状态transitions的rest实用脚本,issue状态改变调整
官方文档链接地址: POST Transition issue Performs an issue transition and, if the transition has a screen, updates the fields from the transition screen. sortByCategory To update the fields on the transition screen, specify the fields in the fiel…...

JAVA 注解
1 概念 Annotation(注解)是 Java 提供的一种对元程序中元素关联信息和元数据(metadata)的途径和方法。Annatation(注解)是一个接口,程序可以通过反射来获取指定程序中元素的 Annotation 对象,然后通过该 An…...
C++面试题准备
文章目录 一、线程1.什么是进程,线程,彼此有什么区别?2.多进程、多线程的优缺点3.什么时候用进程,什么时候用线程4.多进程、多线程同步(通讯)的方法5.父进程、子进程的关系以及区别6.什么是进程上下文、中断上下文7.一…...

使用Java操作Redis
要在Java程序中操作Redis可以使用Jedis开源工具。 一、jedis的下载 如果使用Maven项目,可以把以下内容添加到pom中 <!-- https://mvnrepository.com/artifact/redis.clients/jedis --> <dependency> <groupId>redis.clients</groupId>…...
VRRP配置案例(路由走向分析,端口切换)
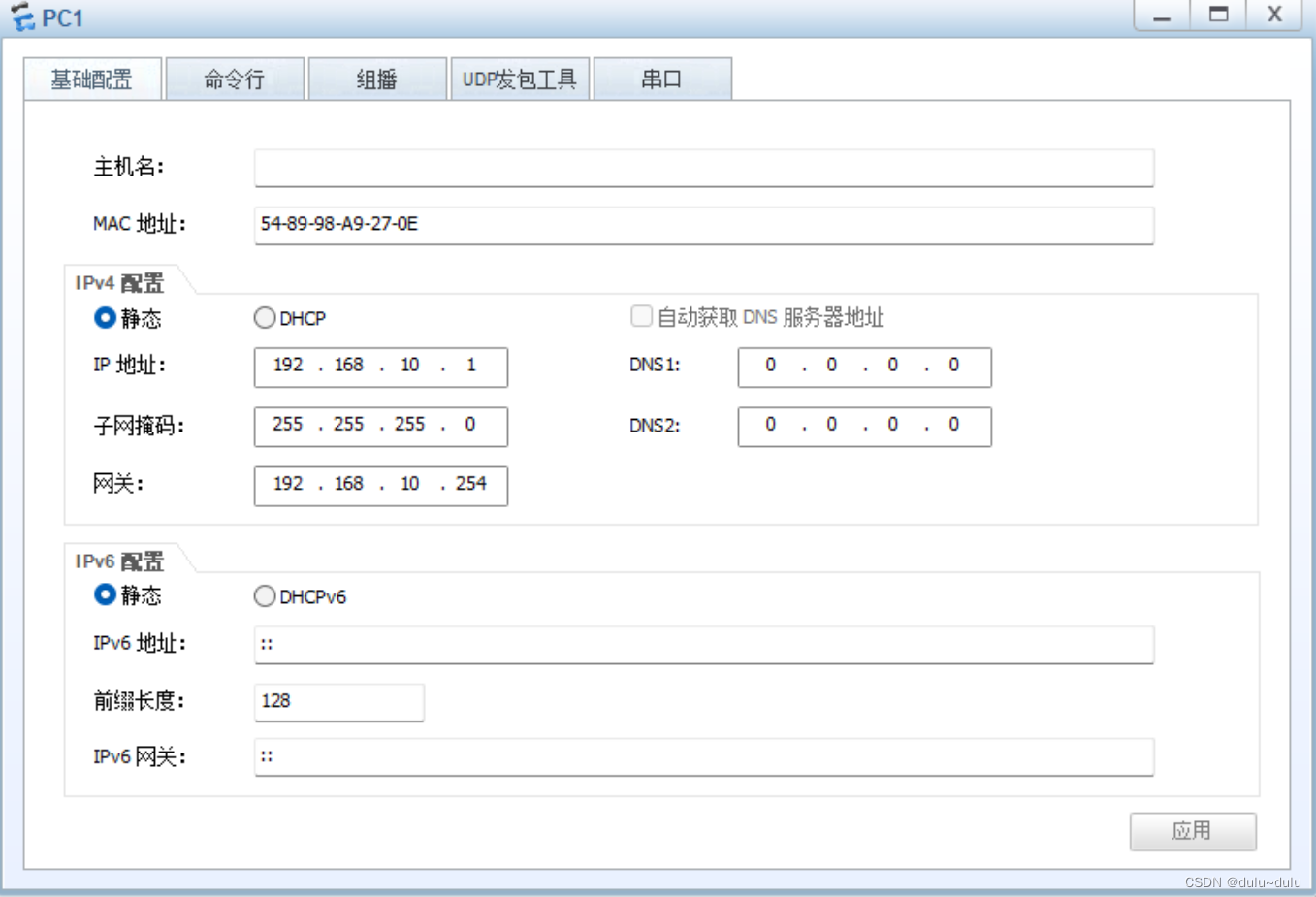
以下配置图为例 PC1的配置 acsw下行为access口,上行为trunk口, 将g0/0/3划分到vlan100中 <Huawei>sys Enter system view, return user view with CtrlZ. [Huawei]sysname acsw [acsw] Sep 11 2023 18:15:48-08:00 acsw DS/4/DATASYNC_CFGCHANGE:O…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
