CF505B Mr. Kitayuta‘s Colorful Graph
Mr. Kitayuta’s Colorful Graph
题面翻译
给出一个 n n n 个点, m m m 条边的无向图,每条边上是有颜色的。有 q q q 组询问
对于第 i i i 组询问,给出点对 u i , v i u_i,v_i ui,vi。求有多少种颜色 c c c 满足:有至少一条 u i u_i ui 到 v i v_i vi 路径,满足该路径上的所有边的颜色都为 c c c
输入格式
第一行两个整数 n , m n,m n,m 分别表示点的个数和边的个数
接下来 m m m 行,每行三个整数 x i , y i , c i x_i,y_i,c_i xi,yi,ci,表示有一条连接点 x i , y i x_i,y_i xi,yi 的边,且该边的颜色为 c i c_i ci
接下来一行一个整数 q q q,表示询问的个数
接下来 q q q 行,每行两个整数 u i , v i u_i,v_i ui,vi,表示一组询问
输出格式
对于每一组询问,在单独的一行输出一个整数,表示满足上述要求的颜色种数
说明与提示
2 ≤ n ≤ 100 2 \le n \le 100 2≤n≤100
1 ≤ m , q ≤ 100 1 \le m,q \le 100 1≤m,q≤100
1 ≤ x i , y i , u i , v i ≤ n 1\le x_i,y_i,u_i,v_i \le n 1≤xi,yi,ui,vi≤n
1 ≤ c i ≤ m 1 \le c_i \le m 1≤ci≤m
感谢 @_Wolverine 提供的翻译
题目描述
Mr. Kitayuta has just bought an undirected graph consisting of $ n $ vertices and $ m $ edges. The vertices of the graph are numbered from 1 to $ n $ . Each edge, namely edge $ i $ , has a color $ c_{i} $ , connecting vertex $ a_{i} $ and $ b_{i} $ .
Mr. Kitayuta wants you to process the following $ q $ queries.
In the $ i $ -th query, he gives you two integers — $ u_{i} $ and $ v_{i} $ .
Find the number of the colors that satisfy the following condition: the edges of that color connect vertex $ u_{i} $ and vertex $ v_{i} $ directly or indirectly.
输入格式
The first line of the input contains space-separated two integers — $ n $ and $ m $ ( $ 2<=n<=100,1<=m<=100 $ ), denoting the number of the vertices and the number of the edges, respectively.
The next $ m $ lines contain space-separated three integers — $ a_{i} $ , $ b_{i} $ ( $ 1<=a_{i}<b_{i}<=n $ ) and $ c_{i} $ ( $ 1<=c_{i}<=m $ ). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if $ i≠j $ , $ (a_{i},b_{i},c_{i})≠(a_{j},b_{j},c_{j}) $ .
The next line contains a integer — $ q $ ( $ 1<=q<=100 $ ), denoting the number of the queries.
Then follows $ q $ lines, containing space-separated two integers — $ u_{i} $ and $ v_{i} $ ( $ 1<=u_{i},v_{i}<=n $ ). It is guaranteed that $ u_{i}≠v_{i} $ .
输出格式
For each query, print the answer in a separate line.
样例 #1
样例输入 #1
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4
样例输出 #1
2
1
0
样例 #2
样例输入 #2
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4
样例输出 #2
1
1
1
1
2
提示
Let’s consider the first sample.
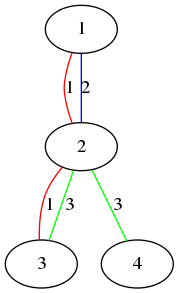 The figure above shows the first sample. - Vertex $ 1 $ and vertex $ 2 $ are connected by color $ 1 $ and $ 2 $ .
The figure above shows the first sample. - Vertex $ 1 $ and vertex $ 2 $ are connected by color $ 1 $ and $ 2 $ .
- Vertex $ 3 $ and vertex $ 4 $ are connected by color $ 3 $ .
- Vertex $ 1 $ and vertex $ 4 $ are not connected by any single color.
思路
(1)并查集
一个二维并查集,一个记录颜色,一个记录点。
(2)Floyed
普通Floyed加一维颜色。数据只有100四维循环不会T。
AC code
(1)并查集
#include<bits/stdc++.h>using namespace std;int fa[1000][1000];
int n, m, t;int find(int x, int i)
{if (fa[x][i] == x) return x;return fa[x][i] = find(fa[x][i], i);
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)fa[i][j] = i; for (int i = 1; i <= m; ++i){int u, v, z;cin >> u >> v >> z;fa[find(u, z)][z] = find(v,z); }cin >> t;while (t--){int u, v, ans = 0;cin >> u >> v;for(int i = 1; i <= m;i++)if (find(u,i) == find(v,i)) ans++; cout << ans << endl;}return 0;
}
(2)Floyed
#include<bits/stdc++.h>using namespace std;int a[101][101][101];int main()
{int n, m;cin >> n >> m;for(int i = 1; i <= m; i++){int u, v, q;cin >> u >> v >> q;a[u][v][q] = 1;a[v][u][q] = 1;}for (int k = 1; k <= n; k++)for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)for (int c = 1; c <= m; c++)if (a[i][k][c] == 1 && a[k][j][c] == 1)a[i][j][c] = 1;int q;cin >> q;for (int i = 1; i <= q; i++){int u, v;cin >> u >> v;int sum = 0;for(int j = 1; j <= m; j++)if(a[u][v][j] == 1)sum++;cout << sum << endl;}return 0;
}相关文章:

CF505B Mr. Kitayuta‘s Colorful Graph
Mr. Kitayuta’s Colorful Graph 题面翻译 给出一个 n n n 个点, m m m 条边的无向图,每条边上是有颜色的。有 q q q 组询问 对于第 i i i 组询问,给出点对 u i , v i u_i,v_i ui,vi。求有多少种颜色 c c c 满足:有至…...
c#设计模式-结构型模式 之 组合模式
🚀简介 组合模式又名部分整体模式,是一种 结构型设计模式 ,是用于把一组相似的对象当作一个 单一的对象 。组合模式 依据树形结构来组合对象 ,用来表示部分以及整体层,它可以让你将对象组合成树形结构,并且…...

【Rust日报】2023-09-30 使用Rust做web抓取
CockroachDB 用rust重新实现 嘿,伙计们,我在 Rust 中实现了一个分布式 SQL 数据库。它就像 CockroachDB 和谷歌Google Spanner。告诉我你的想法。 注意: 这不是生产级别的数据库,这是一个以学习为目的的项目。有许多特性,但是缺少…...
【密评】商用密码应用安全性评估从业人员考核题库(三)
商用密码应用安全性评估从业人员考核题库(三) 国密局给的参考题库5000道只是基础题,后续更新完5000还会继续更其他高质量题库,持续学习,共同进步。 501 多项选择题 《个人信息保护法》要求个人信息处理者应当采取哪些…...

MySQL进阶_查询优化和索引优化
文章目录 第一节、索引失效案例1.1 数据准备1.2 全值匹配我最爱1.3 最佳左前缀法则 第一节、索引失效案例 可以从以下维度对数据库进行优化: 索引失效、没有充分利用到索引–索引建立关联查询太多JOIN (设计缺陷或不得已的需求)–SQL优化服务器调优及各个参数设置…...

Hadoop2复安装过程详细步骤
1、在vmware中更改了虚拟机的网络类型,--->NAT方式,(虚拟交换机的ip可以从vmvare的edit-->vertual network editor看到) 2、根据这个交换机(网关)的地址,来设置我们的客户端windows7的ip&…...

【Java-LangChain:面向开发者的提示工程-7】文本扩展
第七章 文本扩展 扩展是将短文本(例如一组说明或主题列表)输入到大型语言模型中,让模型生成更长的文本(例如基于某个主题的电子邮件或论文)。这种应用是一把双刃剑,好处例如将大型语言模型用作头脑风暴的伙…...
竞赛 基于设深度学习的人脸性别年龄识别系统
文章目录 0 前言1 课题描述2 实现效果3 算法实现原理3.1 数据集3.2 深度学习识别算法3.3 特征提取主干网络3.4 总体实现流程 4 具体实现4.1 预训练数据格式4.2 部分实现代码 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习机器视觉的…...

从技能需求到就业前景,了解前端和后端开发的优缺点和个人选择
文章目录 每日一句正能量一、引言前端开发后端开发 二、两者的对比分析三、技能转换和跨领域工作四:介绍全栈开发后记 每日一句正能量 命运决定的不是你的人生,能决定你人生的只有自己。 一、引言 前端和后端是Web开发中两个不可或缺的领域。前端开发主…...

Flutter笔记:AnimationMean、AnimationMax 和 AnimationMin 三个类的用法
Flutter笔记 AnimationMean、AnimationMax 和 AnimationMin三个类的用法 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/…...
华为云云耀云服务器L实例评测|云耀云服务器L实例部署Gogs服务器
华为云云耀云服务器L实例评测|云耀云服务器L实例部署Gogs服务器 一、云耀云服务器L实例介绍1.1 云耀云服务器L实例简介1.2 云耀云服务器L实例特点 二、Gogs介绍2.1 Gogs简介2.2 Gogs特点 三、本次实践介绍3.1 本次实践简介3.2 本次环境规划 四、远程登录华为云云耀云…...
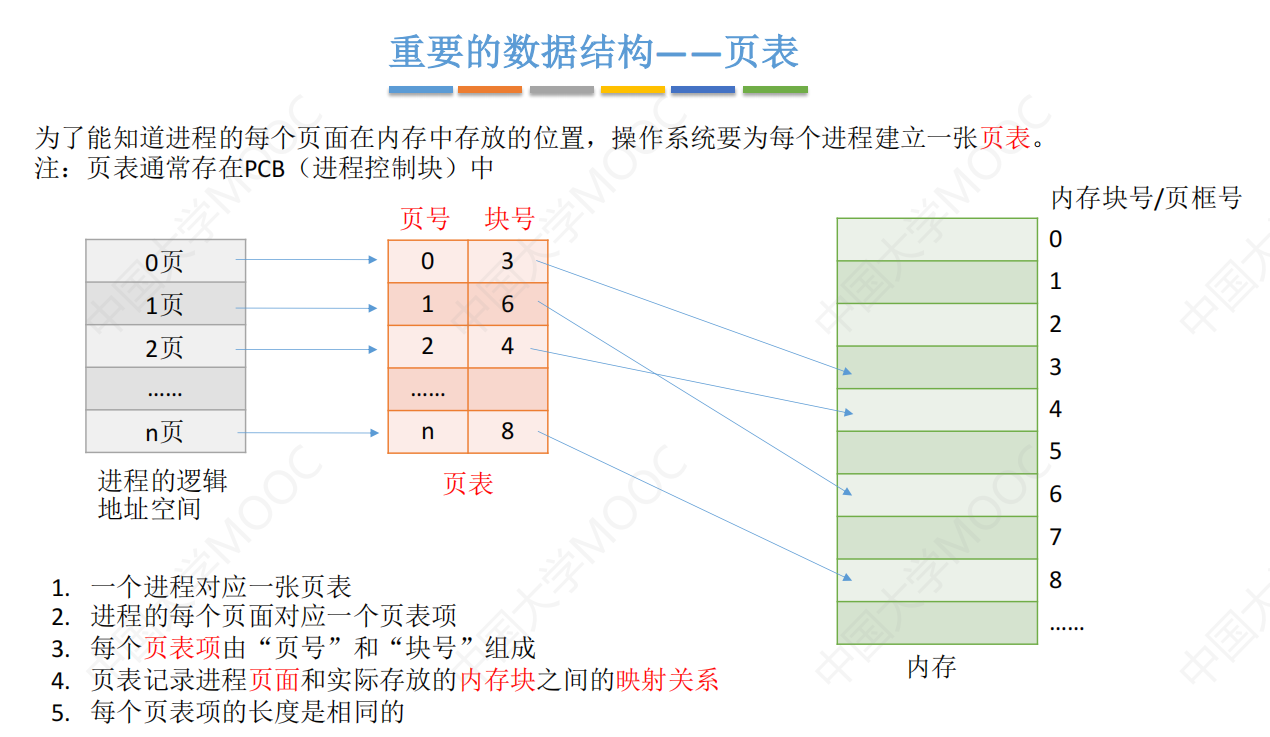
操作系统--分页存储管理
一、概念介绍 分页存储:一是分内存地址,二是分逻辑地址。 1.分内存地址 将内存空间分为一个个大小相等的分区。比如,每个分区4KB。 每个分区就是一个“页框”,每个页框有个编号,即“页框号”,“页框号”…...

【算法练习Day10】有效的括号删除字符串中的所有相邻重复项逆波兰表达式求值
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:练题 🎯长路漫漫浩浩,万事皆有期待 文章目录 有效的括号删除字符串中的所…...

10.1 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、自动驾驶一周资讯 - 苹果汽车项目泡汤?纵目科技IPO终止,腾讯与岚图汽车合作升级,158亿元现金收购比亚迪“史上最大”并购案 自动驾驶一周资讯 - 苹果汽车…...

Redis中Set类型的操作
Set的结构与list相似,但底层存储结构是hashtable,因此它的值是唯一的,同时添加的顺序与保存的顺序并不一致。每一个Set类型的key中可以存储2^32-1个元素。 一、应用场景 1、保存用户的收藏 在小说网站中保存用户的收藏,收藏 的小…...
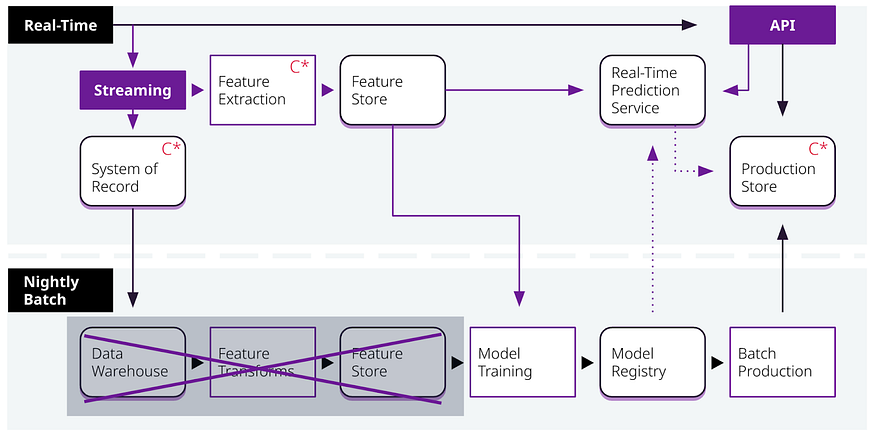
正确完成实时 AI
发表于 构建真实世界的实时 AI 一、说明 我们知道,当前的AI进展是扎根于历史数据,这就造成一个事实,模型总是赶不上实时进展,模型的洞察力不够尖锐,或者,时间损失等,本篇对这一系列AI的短板展开…...

深度学习笔记之线性代数
深度学习笔记之线性代数 一、向量 在数学表示法中,向量通常记为粗体小写的符号(例如,x,y,z)当向量表示数据集中的样本时,它们的值具有一定的现实意义。例如研究医院患者可能面临的心脏病发作风…...

Python与Scrapy:构建强大的网络爬虫
网络爬虫是一种用于自动化获取互联网信息的工具,在数据采集和处理方面具有重要的作用。Python语言和Scrapy框架是构建强大网络爬虫的理想选择。本文将分享使用Python和Scrapy构建强大的网络爬虫的方法和技巧,帮助您快速入门并实现实际操作价值。 一、Pyt…...

kind 安装 k8s 集群
在某些时候可能需要快速的部署一个k8s集群用于测试,不想部署复杂的k8s集群环境,这个时候我们就可以使用kind来部署一个k8s集群了,下面是使用kind部署的过程 一、安装单节点集群 1、下载kind二进制文件 [rootlocalhost knid]# curl -Lo ./kin…...

Leetcode 2871. Split Array Into Maximum Number of Subarrays
Leetcode 2871. Split Array Into Maximum Number of Subarrays 1. 解题思路2. 代码实现 题目链接:2871. Split Array Into Maximum Number of Subarrays 1. 解题思路 这一题实现上其实还是比较简单的,就是一个贪婪算法,主要就是思路上需要…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
