2024级199管理类联考之数学基础(上篇)
管理类考试介绍
- 管理综合200分,时间3小时
- 数学:75分/25题,是拉开差距的核心模块
- 问题求解题:15个,5选一
- 条件充分性判断:10个,结合两个条件选择答案
- 条件一充分,条件二不充分:A
- 条件一不充分,条件二充分:B
- 条件一充分,条件二充分:D
- 条件一不充分,条件二不充分,联合充分:C
- 条件一不充分,条件二不充分,联合不充分:E
- 逻辑:60分/30题,形式、论证、分析推理【大部分40-50分】
- 写作:65分/2篇作文,论证有效性分析600字,论说文700字【大部分35-45分】
- 数学:75分/25题,是拉开差距的核心模块
- 英语二 100分,3小时
数学概述
算术(平均1-2题)
有理数和无理数
实数分为有理数和无理数,两者区别在于能否写成两个整数之比
- 有理数包括整数和分数
- 整数:正整数、0、负整数
- 自然数:0和正整数统称为自然数,即非负整数
- 无理数:无限不循环小数,如e、log等
- 经常考察一个式子同时含有有理数与无理数部分,整体等于0
- 解题思路: 有理数部分合并,无理数部分合并,分别为0
质数与合数
- 质数/素数:大于1的整数,除了1和自身之外不能被其他正整数整除的数(即约数只有1和质数本身)
- 合数:大于1的整数,除了1和自身之外还能被其他正整数整除的数(即约数包括1、本身以及其他约数)
- 注意
- 1既不是质数也不是合数,2是唯一的偶质数;质因数表示既是一个数的约数又是质数的数
- 20以内8大质数:2,3,5,7,11,13,17,19
奇数偶数
- 奇数:不能被2整除的整数,表示为2k+1
- 偶数:能被2整除的整数,包括0,表示为2k
整除/约数/倍数
- 常见数整除的特征
- 能被2整除的数:个位数字为0、2、4、6、8
- 能被3整除的数:各位数字之和必能被3整除
- 能被4整除的数:末两位数字必能被4整除
- 能被5整除的数:个位数字为0或5
- 能被6整除的数:同时满足能被2和3整除
- 能被8整除的数:末三位数字必能被8整除
- 能被9整除的数:各位数字之和能被9整除
- 能被10整除的数:个位数字为0
- 公约数:几个自然数公有的约数,称为这几个自然数的公约数,公约数中最大的公约数称为这几个自然数的最大公约数
- 最小公倍数:几个自然数公有的倍数(排除0以外)

绝对值非负性
- 正数的绝对值是它本身,负数是它的相反数,零的绝对值还是0
- 几何意义:表示一个实数a在数轴上所对应的点到原点0的距离值,如|x-b| =a表示与b点的距离为a
- 非负符号:绝对值、偶次乘方、开偶次根号
- 常见考试场景:含有绝对值和开偶次根号或者偶次乘方
- 解题思路:保持各项为0即可
绝对值两个模型
- 和模型(函数曲线为平底锅型):存在最小值
- |x-a|+|x-b|几何意义表示数轴上x到a与b点的距离之和,当x在a点与b点之间存在最小值,即最小距离值为|a-b|,x不在两者之间则趋于正无穷.
- 若f(x) = |x-a|+|x-b|+|x-c|,也无最大值,当x在a与c之间时且x=b时存在最小值|c-a|
- 即奇数个点取中间点有最小值,偶数个点取中间两个数之间点有最小值
- 差模型(函数曲线为Z字型):既有最小值也存在最大值
- |x-a|-|x-b|几何意义表示数轴上x到a与b点的距离之差,当x在a点与b点之外时存在最大值|a-b|和最小距离值为-|a-b|
三角不等式(求最值)
- |a + b| <= |a|+|b|;等号成立条件ab>=0;
- |a - b| <= |a|+|b|;等号成立条件ab<=0;
- 三角不等式主要考察取等号条件,消去参数是核心
比和比例
- 比例基本性质
- 比例的前项和后项同时乘或除以不含0的相同的数,比值不变
- a:b=c:d <==> b:a=d:c<=> a:c=b:d<=>c:a=d:b
- 比例定理
- 合比定理:a/b = c/d <=> (a+b)/b=(c+d)/d
- 分比定理:a/b = c/d <=> (a-b)/b=(c-d)/d
- 合分比定理:a/b = c/d <=> (a+b)/a-b=(c+d)/c-d
- 等比定理:a/b = c/d = e/f =a+c+e/b+d+f(b+d+f !=0)
- 解题思路
- 分数比化解为整数比
- 需要引入比例系数k,化抽象比例为具体数值计算求解

平均值定理(均值不等式)
- 算术平均数:x1+x2+...+xn/n
- 几何平均数:设n个正数x1...xn称x=n次根号下x1..xn
- 基本定理
- x1...xn为正数时,它们的算术平均值不小于几何平均值,即x1...xn/n>=n次根号下x1...xn,当且仅当x1=...=xn,等号成立
- 若a>0,b>0,则a+b/2>=根号下ab(a+b>=2根号下ab),当且仅当a=b时等号成立(一正二定三相等)
- 积为定值,则求和存在最小值
- 和为定值,则求积存在最大值
- a+1/a>=2(a>0)当且仅当a=1时取最小值2,即对正数而言互为倒数的两个数之和不小于2
- 扩展
- a+b+c>=3*3次根号下abc(a、b、c>0)当且仅当a=b=c时取得等号
- a+b+c+d>=4*4次根号下abcd(a、b、c、d>0)当且仅当a=b=c=d时取得等号

整式与分式(平均1-2题)
因式分解
- 概念:把一个多项式化成几个整式的积的形式,本质就是化和为积,例如x^2 + 3x +2 = (x+2)(x+1)
- 注意:因式分解必须在指定的范围内分解到不能再分解为止
- 常用方法
- 分组分解法:例如am+bm+an+bn=(a+b)(m+n)
- 平方差公式:a^2-b^2=(a-b)(a+b)
- 完全平方公式:(a+_b)^2=a^2+-2ab+b^2
- 立方和与立方差公式:a^3+-b^3=(a+-b)(a^2-+ab+b^2)
- 三项完全平方和公式:(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc
- 完全立方和公式:(a+b)^3=a^3+3a^2b+3ab^2+b^3
- 拓展公式:(a-b)^2+(b-c)^2+(a-c)^2=2[a^2+b^2+c^2-ab-ac-bc]
- 十字相乘法:如x^2+5x+6=(x+2)(x+3)
因式定理
- 出题模式
- 代数式能被某个式子整除
- 某个式子是代数式的因式
- 代数式含有某某因式
- 解题模式
- 令因式为零,求得x的值
- 因式为根,根带入原式,代数式为零



代数式化简
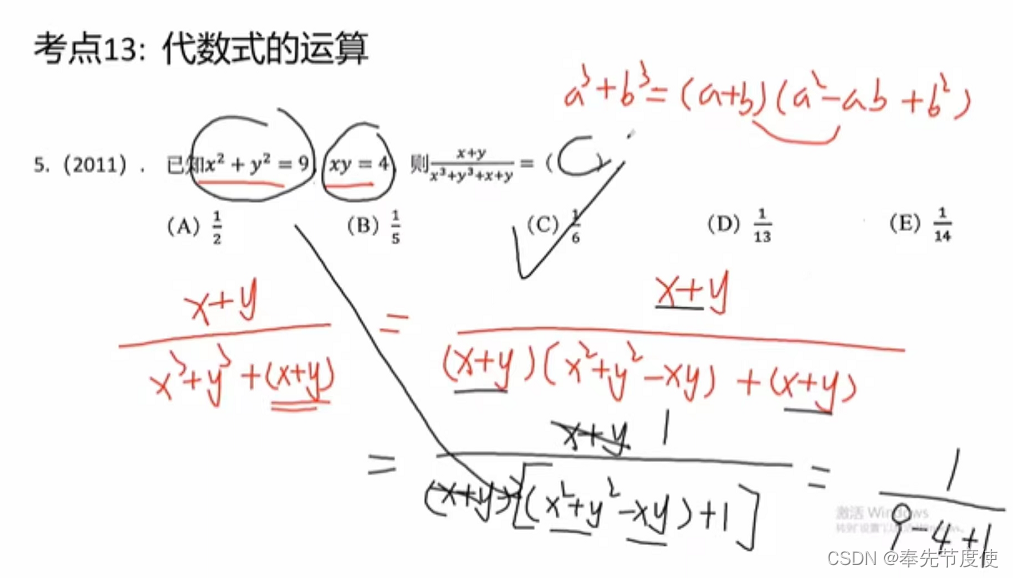

裂项相消法(数列求和或分式化简)
- 概念:实质就是因式分解的一种形式变换,以若干个分式相加,每个分式的分子都是1,然后重新组合,使之能消去一些项,最终达到求和目的
- 1/n(n+k)=1/k(1/n-1/(n+k)),即1/(大)(小)=1/大-小(1/小-1/大)

集合与函数(平均1-2题)
集合
- 性质
- 确定性:元素在一个集合或不在一个集合,不能模糊
- 相异性:集合中的元素不能重复
- 无序性:集合中的元素没有顺序要求
- 集合中运算包括并、交、补大部分使用文氏图表示

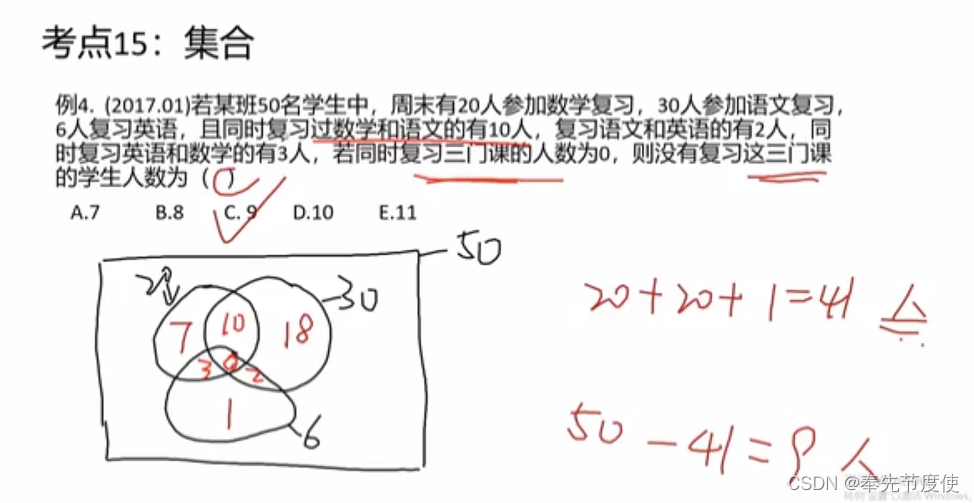
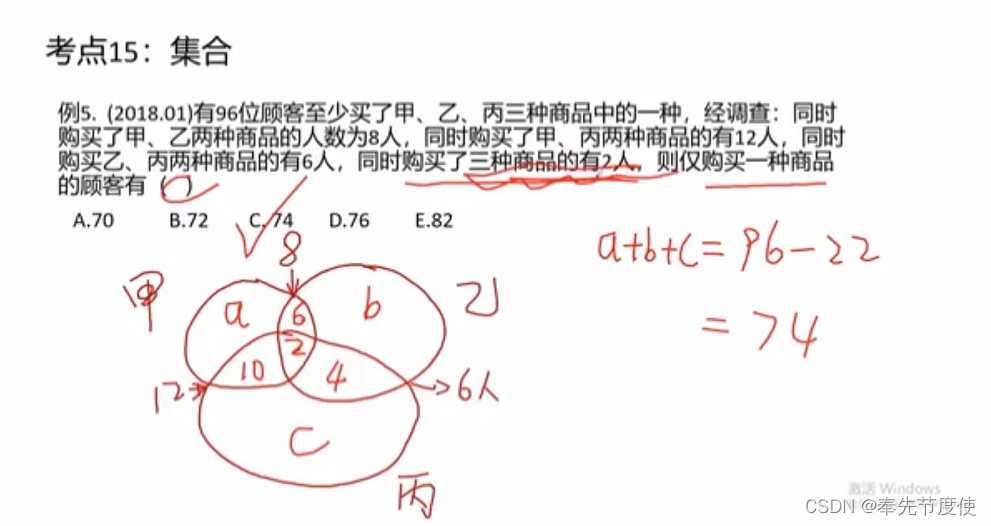
一元一次函数
- 定义:一般在某一变化过程中有两个变量x和y,如果给定一个x,相应确定一个y值,那么称y是x的函数,x是自变量,y是因变量
- 若两个变量x,y关系可以表示为y=kx+b(k、b为常数,k!=0),则称y是x的一次函数,当b=0时则y=kx(k!=0)称y是x的正比例函数。注意:一次函数都是一条直线

一元二次函数
- 基本定义
- y=ax^2+bx+c(a!=0,a、b、c是常数),对称轴x=-b/2a,顶点坐标(-b/2a,4ac-b^2/4a),最值在顶点处取得(a>0为最小值,a<0表示函数有最大值)
- 表达式
- 一般式:y=ax^2+bx+c
- 顶点式:y=a(x+b/2a)^2+4ac-b2/4a
- 两根式:y=a(x-x1)(x-x2)
- x1,x2表示函数与x轴交点的横坐标/函数的零点/对应一元二次方程的两个根
- 一元二次函数性质
- a决定抛物线的开口方向,a>0向上,a<0向下
- 对称轴-b/2a>0表示在y轴右侧,<0表示y轴左侧,=0表示对称轴就是y轴
- c>0表示抛物线与y轴的交点在原点上方,=0表示过原点,<0表示在原点下方
- 判别式吧b^2-4ac决定抛物线与x轴的交点个数,>0表示有两个,=0有一个且顶点在x轴上,<0表示无交点
- 若a+b+c=0,则抛物线过点(1,0);若a-b+c=0,则抛物线过点(-1,0)



指数函数与对数函数
- 指数函数
- 定义:y=a^x(a>0且a!=1)称为指数函数,x为自变量
- 运算法则
- a^m * a^n = a^m+n
- a^m / a^n = a^m-n
- (a^m)^n = a^mn
- (ab)^m = a^m*b^m
- a^0 = 1;a^-p = 1/a^p(a!=0)
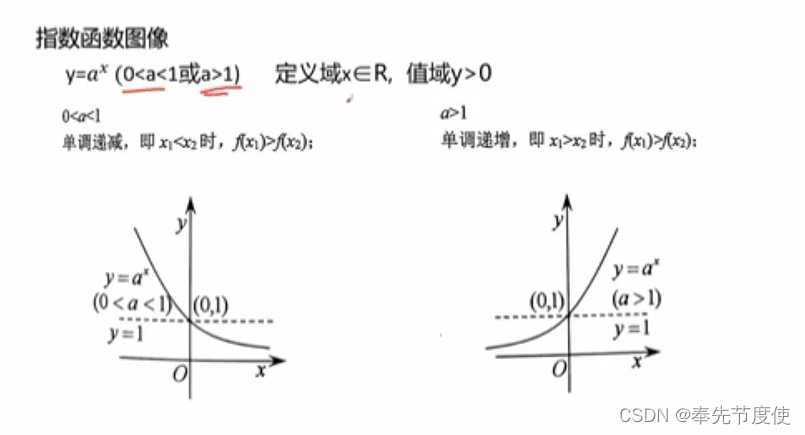

- 对数函数
- 定义:y=logaX(a>0且a!=1,x>0),a为底数,x为真数,y是以a为底x的对数
- 与指数互为反函数:a^m = b 《=》m=logab
- 运算法则
- logaMN=logaM+logaN
- logaM/N=logaM-logaN
- logaM^n=nlogaM
- loga^Nb^M=M/Nlogab
- 换底公式
- logaN=logbN/logba
- loga1=0;logaa=1;lg2+lg5=1;
- 定义:y=logaX(a>0且a!=1,x>0),a为底数,x为真数,y是以a为底x的对数


方程与不等式(平均2-4题)
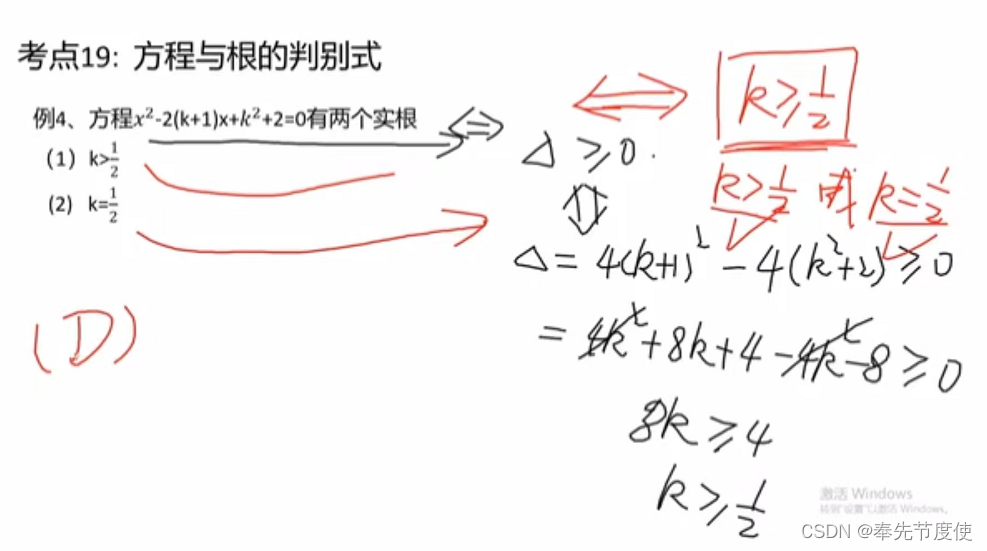
方程与根的判别式
- 一元一次方程:只含有一个未知数,并且未知数的最高次数为1,其中方程ax+b=0(x为未知数,a!=0)为标准一元一次方程形式,方程的解为x=-b/a;
- 一元二次方程:ax^2+bx+c=0(a!=0),a是二次项系数,b是一次项系数,c是常数项
- 根的判别式b^2-4ac
- >0时,方程有两个不等实根,根x=-b+-根号下b^2-4ac/2a
- =0时,存在两个相等实根,x=-b/2a
- <0时,方程无实根
- b^2-4ac联考中自然语言表达
- b^2-4ac=0
- 方程有两个相等实根/重实根
- 函数抛物线与x轴有且仅有一个交点/零点
- 抛物线与x轴相切
- 函数是一个完全平方公式
- 函数抛物线的最大/小值为0
- 仅存在一个x使得ax^2+bx+c=0成立
- b^2-4ac>0
- 方程有两个不相等的实数根
- 抛物线与x轴相交/有两个交点
- 函数或方程有两个零点
- 直线与抛物线有两个交点
- b^2-4ac<0
- 方程没有实数根
- 函数抛物线与x轴没有交点/零点
- 抛物线与x轴相离
- 直线与抛物线无交点
- 二次函数图像恒位于x轴上方/下方
- b^2-4ac>=0
- 方程有两个实数根
- 方程有两个正根
- 方程有两个负根
- 方程有根
- b^2-4ac=0
- 根的判别式b^2-4ac
- 是否对二次项系数a=0进行讨论
- 如果题目中明确二次函 数、一元二次方程、一元二次不等式、抛物线等则默认a!=0
- 若题目知识表示是函数、方程、不等式,则需要对a是否为0进行分类讨论
韦达定理
- 定义:ax^2+bx+c=0(a!=0)的两个根为x1,x2,则
- x1+x2=-b/a
- x1*x2=c/a
- 扩展公式
- x1^2+x2^2=(x1+x2)^2-2x1x2
- x1^3+x2^3=(x1+x2)[(x1+x2)^2-3x1x2]
- |x1-x2|=根号下b^2-4ac/|a|
- |x1-x2|不同自然语言表达形式
- 方程两根之差的绝对值
- 方程两根之间的距离
- 函数抛物线截得x轴的长度
- 函数抛物线与两坐标轴围成的三角形的底边长
- |x1-x2|不同自然语言表达形式

方程根的分布
- 根的分布是个综合问题,需要同时使用判别式和韦达定理
- 一元次方程ax^2+bx+c=0(a!=0)有两个正根
- b^2-4ac>=0
- x1+x2=-b/a>0
- x1x2=c/a>0
- 一元次方程ax^2+bx+c=0(a!=0)有两个负根
- b^2-4ac>=0
- x1+x2=-b/a<0
- x1x2=c/a>0
- 一元次方程ax^2+bx+c=0(a!=0)有一个负根,一个正根
- b^2-4ac>0
- x1x2=c/a<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个根x1,x2且满足m<x1<n,p<x2<q

- f(m)f(n)<0
- f(p)f(q)<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个根x1,x2且一根大于k,一根小于k
- 则无论a>0还是a<0都有af(k)<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个正根
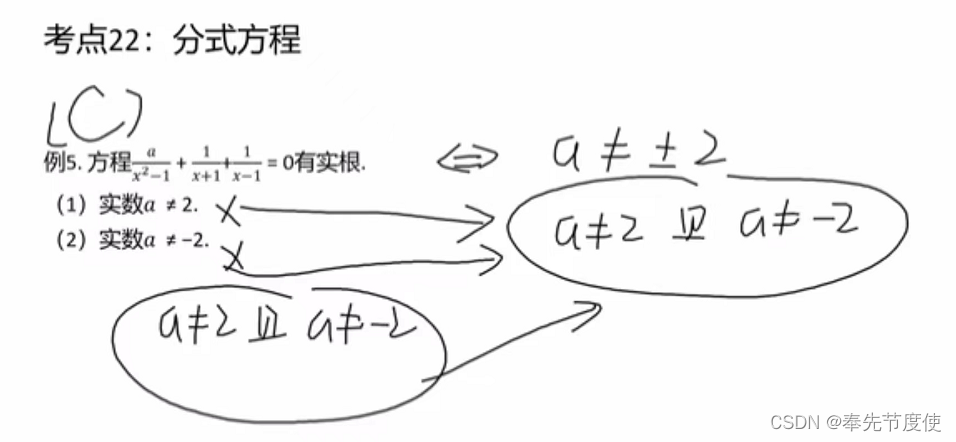
分式方程
- 思路就是将分式方程转换成整式方程
- 特殊解法:换元法(整体思维),还需要考虑是否存在增根等
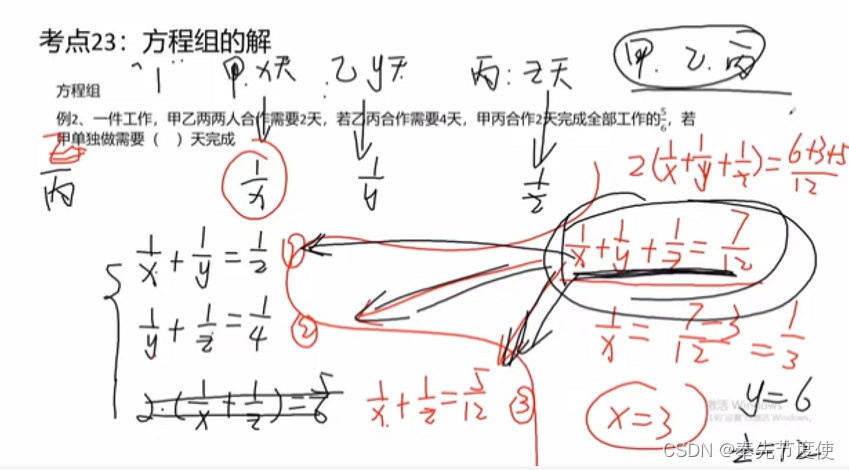
方程组的解
不等式的性质
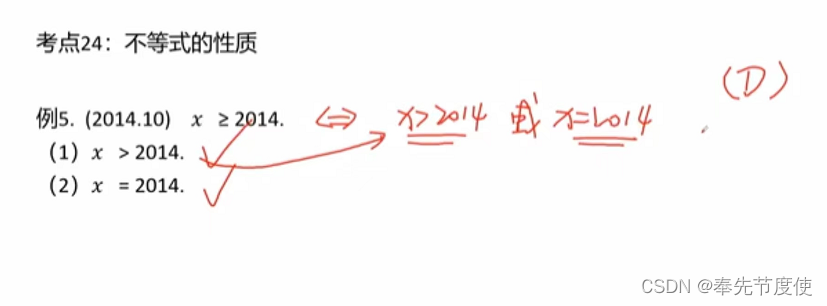
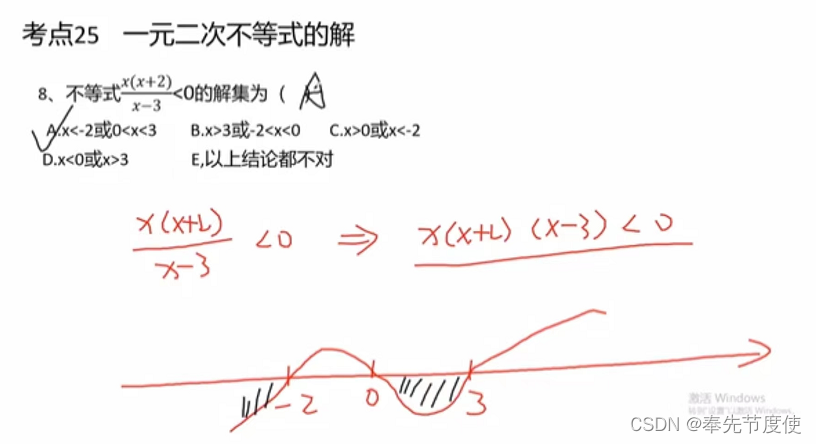
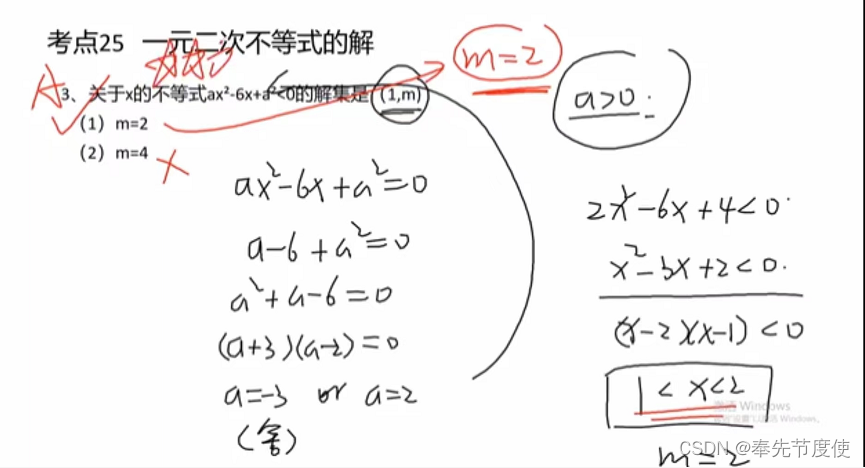
一元二次不等式的解
- 基本概念:不等式中含有一个未知数,未知数的次数为2,且不等式两边都是整式
- 解题思路:不等式看做方程式,然后结合抛物线法(数形结合思想)
- 一元二次不等式的解法

- 不等式解集的边界即为方程的根/零点/与x轴的交点

绝对值不等式(难点)
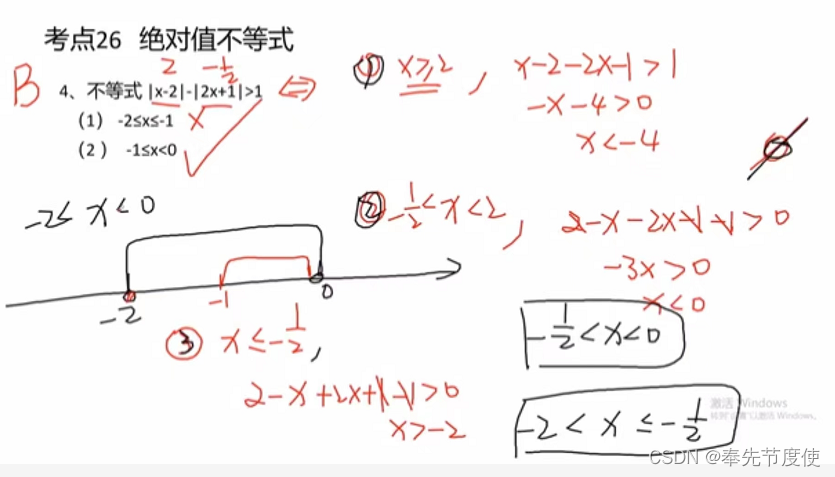
- 解题思路:解含有绝对值不等式的关键是去掉式子中的绝对值符号,常用方法如下
- 平方法:需要确保两边均为非负性才能平方
- 定义法分类讨论
- |f(x)|>f(x),如|x/x-1|>x/x-1
- f(x)>=0时|f(x)|=f(x)
- f(x)<0时|f(x)|=-f(x)
- |f(x)|<g(x)时需要注意g(x)自带定义域
- |f(x)|>f(x),如|x/x-1|>x/x-1
- 公式法
- |f(x)|<a,a>0时则有-a<f(x)<a
- |f(x)|>a,a>0时则有f(x)>a或者f(x)<-a


数列(平均2-3题)
数列相关定义
- 定义:数列是按照一定顺序排列着的一列数
- an与{an}概念不同,an表示数列的第n项,{an}表示数列
- 数列和集合区别
- 集合元素确定、无序、互异
- 数列元素确定、有序、可重复
- an与S(前n项和)关系
- an=S1(n=1)
- an=Sn=Sn-1(n>=2)
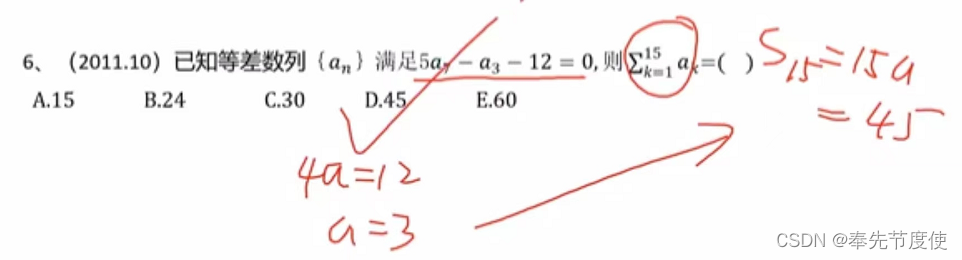
等差数列
- 定义:如果一个数列从第二项起,每一项与它前一项的差等于同一个常数
- 该常数为公差d,可正可负,可0,为0时表示常数项
- 通项公式
- an = a1 +(n-1)d
- an = am +(n-m)d 《=》d=an-am / n-m(n!=m)
- 扩展
- 常数列思想:题目中只有单一条件,此时将每个数列项看做常数项
- 等差中项/均值:如a,b,c为等差数列,则2b=a+c
- 等差数列前n项和公式
- sn=n(a1+an)/2 《=》sn=d/2n^2+(a1-d/2)n,即sn是关于n的二次函数(常数项为0)
- 即可推出d>0,Sn有最小值,d<0有最大值
- sn=An^2+Bn+C,若C=0则为等差数列,若C!=0则从第二项开始是等差数列
- sn=n(a1+an)/2 《=》sn=d/2n^2+(a1-d/2)n,即sn是关于n的二次函数(常数项为0)
- 等差数列连续几项之和构成的新数列仍然是等差数列,即Sn,S2n-Sn...
- 等差数列判定法
- 定义法:an-an-1=d,则为等差数列
- 通项公式法:an = Pn+q,则为等差数列
- 中项公式法:2an+1=an + an+2,则为等差数列
- 前n项和公式法:sn=An^2 + Bn,则为等差数列


等比数列
- 定义:如果一个数列从第二项起,每一项与它前一项的比值等于同一个常数
- 该常数为公比q,q!=0,当q=1时表示非0的常数列
- 通项公式
- an = a1 * q^n-1
- an = am * q^n-m
- 等比数列前n项和公式
- q!=1时, Sn=a1(1-q^n)/1-q=(a1-a1q^n)/1-q
- q=1时,Sn=na1
- q!=0且q!=1时,则Sn=A-Aq^n《=》Sn=A+Bq^n(A+B=0)
- 等比数列性质:若m+n=p+k,则am*an=ap*ak,特别的若m+n=2p,则am*an=ap^2
- 等比数列判定法
- 定义法:an+1/an=q,则为等比数列
- 通项公式法:an = cq^n,则为等比数列
- 中项公式法:an+1^2=an*an+2,则为等比数列
- 前n项和公式法:Sn=A-Aq^n,则为等比数列
数列综合


相关文章:

2024级199管理类联考之数学基础(上篇)
管理类考试介绍 管理综合200分,时间3小时 数学:75分/25题,是拉开差距的核心模块 问题求解题:15个,5选一条件充分性判断:10个,结合两个条件选择答案 条件一充分,条件二不充分:A条件一不充分,条件二充分:B条件一充分,条…...
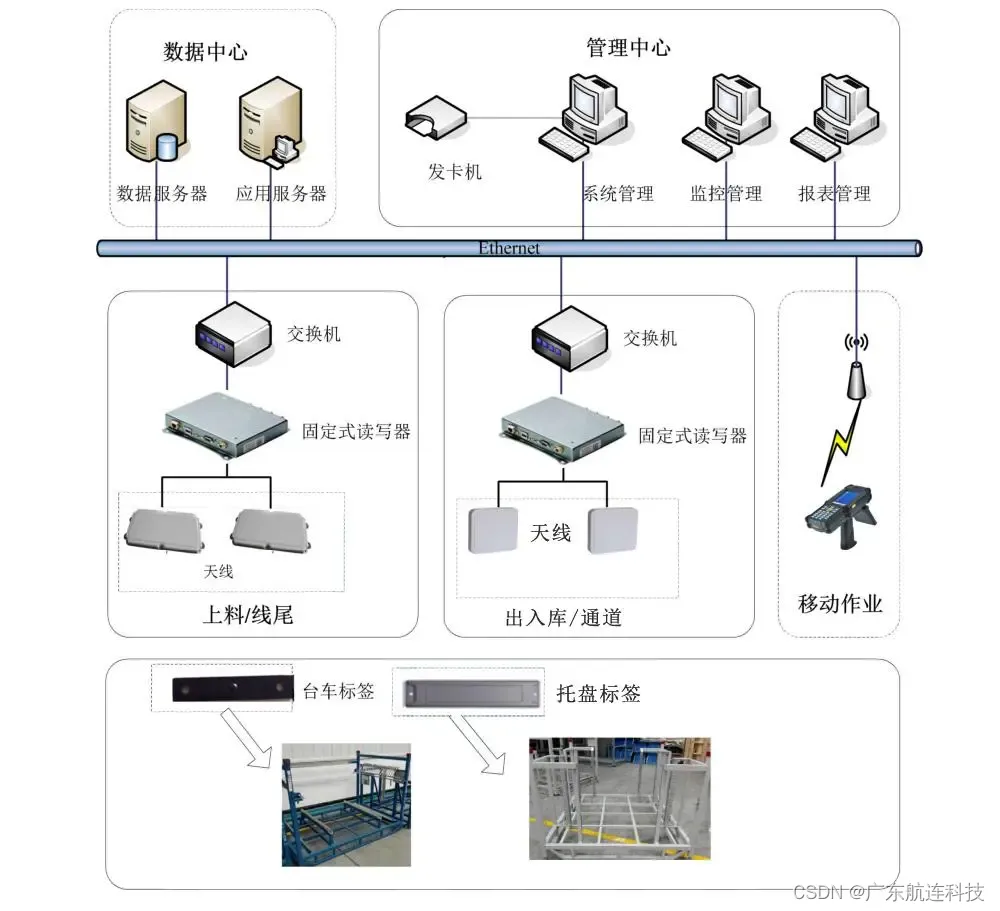
RFID技术引领汽车零部件加工新时代
RFID技术的兴起引领了汽车零部件加工领域的新时代,作为一种利用无线电频率进行自动识别的技术,RFID技术能够快速、准确地识别物体并获取相关数据,在汽车零部件加工中,RFID技术具有重要的应用价值,可以提高生产效率、降…...
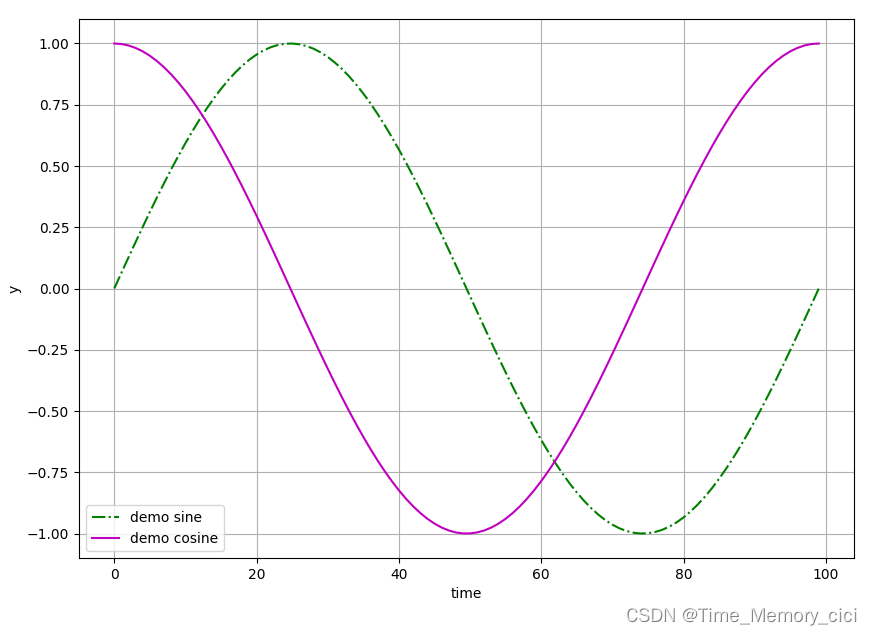
python中使用matplotlib绘图
一、背景 当我们在写python程序时,不可避免的需要将数据可视化,也就是绘制出数据的曲线图,以便我们更直观的观察数据间的变化,和方便对比。此时就要用到matplotlib库了。 matplotlib官方给出的定义是: 翻译过来也就是…...

Qt Creator 使用技巧
使用技巧 功能快捷键解释Switch Header/SourceF4在同名的头文件和源程序文件之间切换Follow Symbol Under CursorF2变量:跳转到声明;函数:声明和定义切换Refactor Rename Symbol Under CursorCtrlShiftR改名称,将替换所有用到这个符号的地方RefactorAdd Definition…...

来看看双阶段目标检测算法趴
🚀 作者 :“码上有钱” 🚀 文章简介 :AI-目标检测算法 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬简介 双阶段目标检测算法是一类深度学习算法,通常分为两个阶段来检测和识别图像中的…...
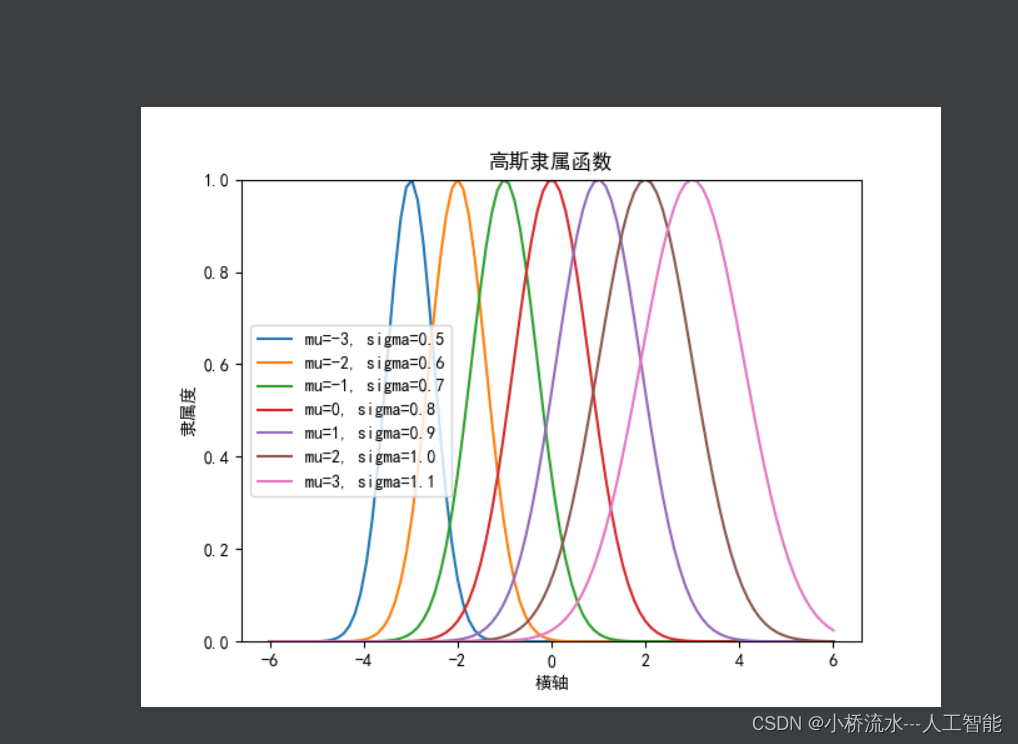
python利用matplotlib绘图,对于中文和负号不显示,显示方框“口口”完美解决办法!!
文章目录 一、问题展示二、问题分析三、解决办法四、结果展示 一、问题展示 二、问题分析 可以发现对中文,以及负号不显示。 三、解决办法 import matplotlib.pyplot as pltplt.rcParams[font.sans-serif] [usimHei] # 显示中文 plt.rcParams[axes.unicode_mi…...
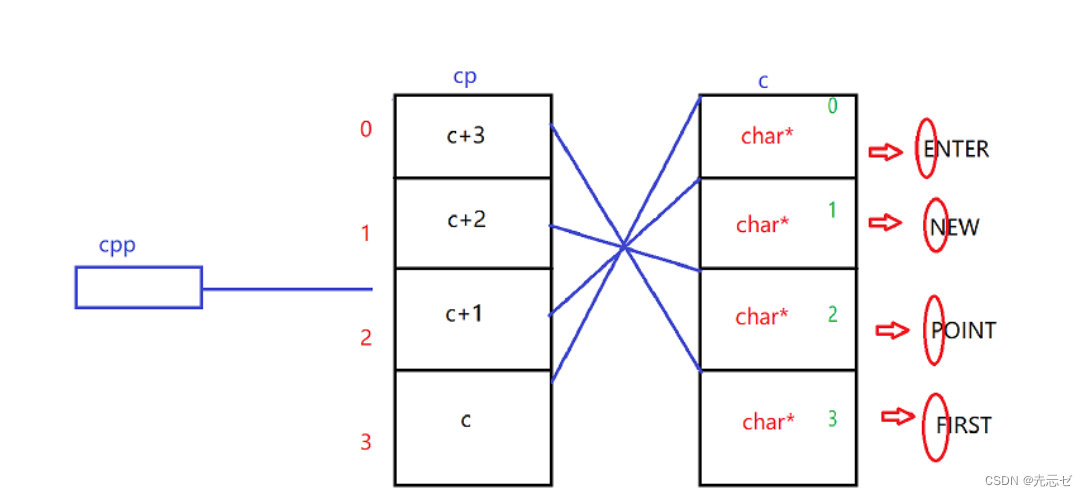
【数组及指针经典笔试题解析】
1.数组和指针笔试题 题目1 int main(){int a[5] { 1,2,3,4,5};int * ptr (int * )(&a 1);printf("%d,%d",*(a 1),*(ptr - 1));return 0;}图文解析: int * ptr …...
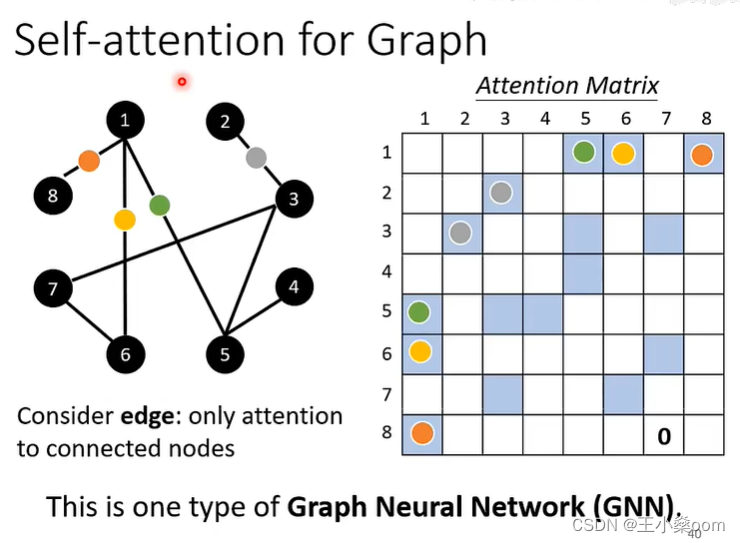
Transformer学习-self-attention
这里写自定义目录标题 Self-attentionMulti-head self-attention用self-attention解决其他问题 Self-attention 用Wq、Wk、Wv分别乘输入向量得到q、k、v向量 用每个q向量乘所有的k向量得到对应项的attention,即用每项的query向量去匹配所有的key向量,得…...

Spring Boot:利用JPA进行数据库的增改
目录 JPA介绍Service接口Service和Autowired示例代码 Dao数据库操作层Repository示例代码 控制器文件示例代码-增加增加成功示例代码-修改修改成功 JPA介绍 JPA(Javaa Persistence API)一种用于持久化 Java 对象到关系型数据库的标准规范。它提供了一种统一的方式来…...
列表的增删改查和遍历
任务概念 什么是任务 任务是一个参数为指针,无法返回的函数,函数体为死循环不能返回任务的实现过程 每个任务是独立的,需要为任务分别分配栈称为任务栈,通常是预定义的全局数组,也可以是动态分配的一段内存空间&#…...

获取网卡上的IP、网关及DNS信息,获取最佳路由,遍历路由表中的条目(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...
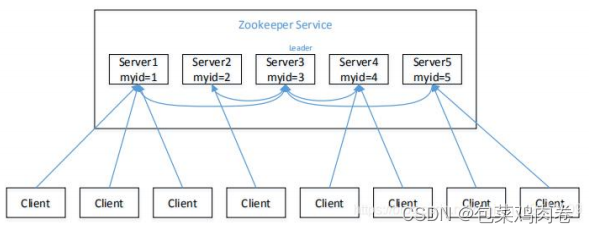
保姆级 -- Zookeeper超详解
1. Zookeeper 是什么(了解) Zookeeper 是一个 分布式协调服务 的开源框架, 主要用来解决分布式集群中应用系统的一致性问题, 例如怎样避免同时操作同一数据造成脏读的问题. ZooKeeper 本质上是 一个分布式的小文件存储系统 . 提供基于类似于文件系统的目录树方式的数据存储, …...

【通意千问】大模型GitHub开源工程学习笔记(2)--使用Qwen进行推理的示例代码解析,及transformers的库使用
使用Transformers来使用模型 如希望使用Qwen-chat进行推理,所需要写的只是如下所示的数行代码。请确保你使用的是最新代码,并指定正确的模型名称和路径,如Qwen/Qwen-7B-Chat和Qwen/Qwen-14B-Chat 这里给出了一段代码 from transformers import AutoModelForCausalLM, Aut…...

从0开始python学习-23.selenium 常见鼠标的操作
注意:必须创建一个事件链对象(ActionChains);最后鼠标事件链完成之后一定要进行事务提交perform()(如果事件链不提交那么所有的鼠标事件都不会执行) 1. 左键单击:click()…...

电气基础——电源、变压器、接触器、断路器、线缆
目录 1.电源 2.变压器 三项电和2相电的转换 3.接触器 4.断路器 5.线缆 1.电源 2.变压器 三项电和2相电的转换 三相电转为2相电 1.变压器 2.相位移转换器 3.电容器 两相电变不了三相电。但是两相电可以通过电容移相后带动三相电机 零线,地线Nÿ…...

步力宝科技爆款产品定位,开创智能物联网新商业
数据显示,中国处于 “亚健康”状态人口数量约占总人口的70%,亚健康是一种临界状态,指介于健康和疾病之间的状态。亚健康是一个动态演变的过程,既有向慢病发展的趋势,也能通过合理的干预使人体重返健康状态,…...
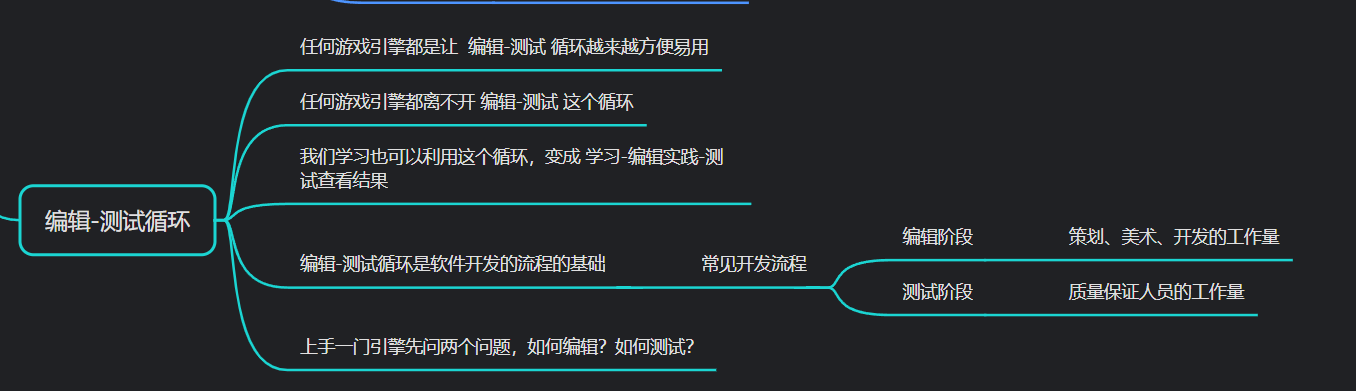
凉鞋的 Unity 笔记 105. 第一个通识:编辑-测试 循环
105. 第一个通识:编辑-测试 循环 在这一篇,我们简单聊聊此教程中所涉及的一个非常重要的概念:循环。 我们在做任何事情都离不开某种循环,比如每天的 24 小时循环,一日三餐循环,清醒-睡觉循环。 在学习一…...
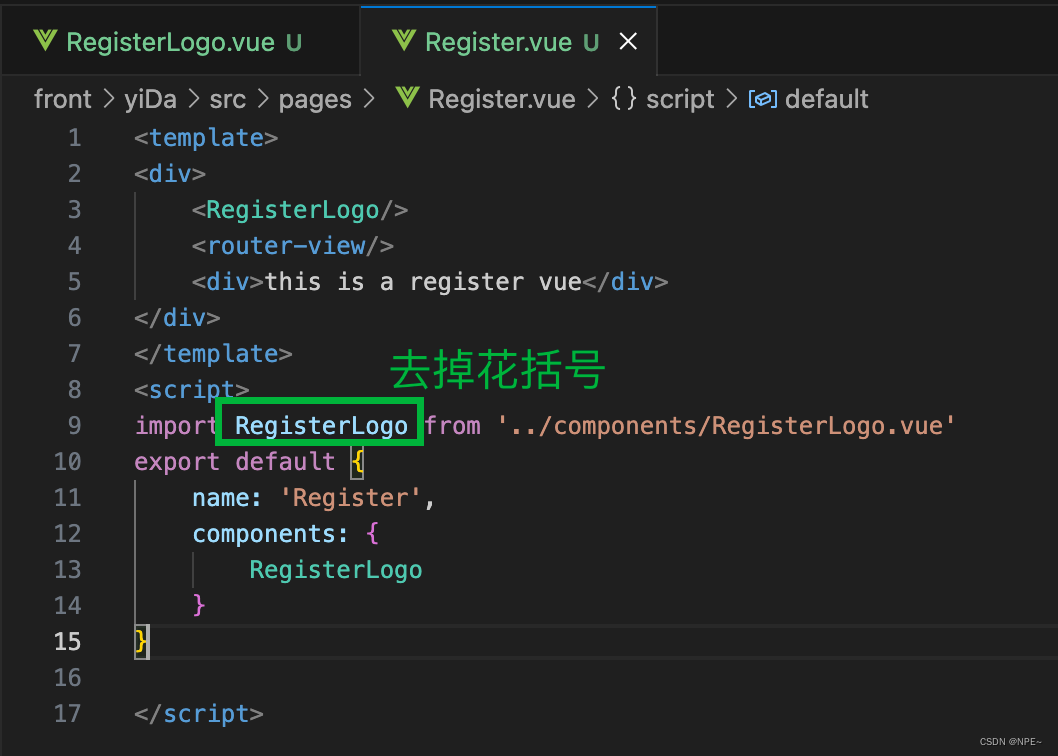
Bug:elementUI样式不起作用、Vue引入组件报错not found等(Vue+ElementUI问题汇总)
前端问题合集:VueElementUI 1. Vue引用Element-UI时,组件无效果解决方案 前提: 已经安装好elementUI依赖 //安装依赖 npm install element-ui //main.js中导入依赖并在全局中使用 import ElementUI from element-ui Vue.use(ElementUI)如果此…...
)
【大麦小米学量化】使用文心一言AI编写股票量化交易策略代码(含演示代码和进阶演示)
文章目录 AI是个宝前言一、文心一言是什么?二、让AI根据策略写出代码1. 策略提示词2. AI给出的策略代码及说明 三、进阶调试总结 AI是个宝 小米听说百度开放了文心一言AI,好奇的跑去问大麦:“文心一言都放开了,什么代码都可以写&a…...
)
软考 系统架构设计师系列知识点之软件架构风格(1)
这个十一注定是一个不能放松、保持“紧”的十一。由于报名了全国计算机技术与软件专业技术资格(水平)考试,11月4号就要考试,因此8天长假绝不能荒废,必须要好好利用起来。现在将各个核心知识点一一进行提炼并做记录。 所…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
