【MATLAB-基于直方图优化的图像去雾技术】
【MATLAB-基于直方图优化的图像去雾技术】
- 1 直方图均衡
- 2 程序实现
- 3 局部直方图处理
1 直方图均衡
直方图是图像的一种统计表达形式。对于一幅灰度图像来说,其灰度统计直方图可以反映该图像中不同灰度级出现的统计情况。一般而言,图像的视觉效果和其直方图有对应关系,通过调整或变换其直方图的形状会对图像的显示效果有很大影响。
直方图均衡化主要用于增强灰度值动态范围偏小的图像的对比度,它的基本思想是把原始图像的灰度统计直方图变换为均匀分布形式,这样就增加了像素灰度值的动态范围,从而达到增强图像整体对比度的效果。
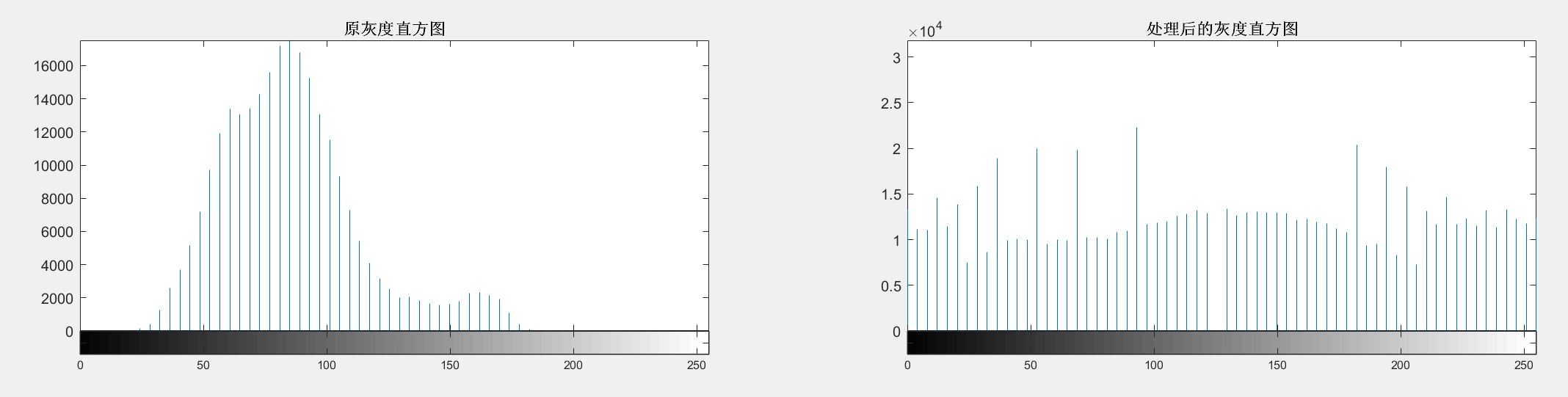
数字图像是离散化的数值矩阵,其直方图可以被视为一个离散函数,表示数字图像中每个灰度级与其出现概率间的统计关系。假设一幅数字图像 f(x,y)的像素总数为 N,r_k表示第 k 个灰度级对应的灰度,n_k表示灰度为r_k 的像素个数即频数,若用横坐标表示灰度级,用纵坐标表示频数,则直方图可被定义为P(r_k)=n_k/N,其中,P(r_k)表示第k灰度出现的相对频数即概率。直方图在一定程度上能够反映数字图像的概貌性描述,包括图像的灰度范围、灰度分布、整幅图像的亮度均值和阴暗对比度等,并可以此为基础进行分析来得出对图像进一步处理的重要依据直方图均衡化也叫作直方图均匀化,就是把给定图像的直方图变换成均匀分布的直方图,是一种较为常用的灰度增强算法。
根据信息论的相关理论,我们可以知道图像在经直方图均衡化后,将会包含更多的信息量进而能突出某些图像特征。假设图像具有 n级灰度,其第级灰度出现的概率为 P_i, 则该级度所含的信息量为:
I ( i ) = p i log 1 p i = − p i log p i I(i)=p_i \log \frac{1}{p_i}=-p_i \log p_i I(i)=pilogpi1=−pilogpi
整幅图像的信息最为:
H = ∑ i = 0 n − 1 I ( i ) = − ∑ i = 0 n − 1 p i log p i H=\sum_{i=0}^{n-1} I(i)=-\sum_{i=0}^{n-1} p_i \log p_i H=∑i=0n−1I(i)=−∑i=0n−1pilogpi
信息论已经证明,具有均匀分布直方图的图像,其信息量H 最大。即当 P 0 = P 1 = . . . = P n − 1 P_0=P_1=...= P_{n-1} P0=P1=...=Pn−1时,H有最大值。
2 程序实现
% 灰度图直方图均衡
% 加载路径和所有文件
clc;clear;close all;
cd(fileparts(mfilename('fullpath')));
addpath(genpath(cd));if ~isfolder('HistGraph')mkdir('HistGraph');
endPath = '.\'; % 设置数据存放的文件夹路径
File = dir(fullfile(Path,'*.jpg')); % 显示文件夹下所有符合后缀名为.txt文件的完整信息
FileNames = {File.name}'; % 提取符合后缀名为.txt的所有文件的文件名,转换为n行1列for i = 1:size(FileNames,1)I = imread(FileNames{i});R = I(:,:,1);M = histeq(R);In = M;figure;subplot(2, 2, 1); imshow(I); title('原图像', 'FontWeight', 'Bold');subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');imwrite(In,['HistGraph\',FileNames{i}],'jpg')Q = I; W = In;subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');subplot(2, 2, 4); imhist(W, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');
end

% 彩色图直方图均衡
clear; close all;
I = imread('images\sweden_input.jpg');
R = I(:,:,1);
G = I(:,:,2);
B = I(:,:,3);
M = histeq(R);
N = histeq(G);
L = histeq(B);
In = cat(3, M, N, L);figure;
subplot(2, 2, 1); imshow(I); title('原图像', 'FontWeight', 'Bold');
subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');Q = rgb2gray(I);
W = rgb2gray(In);
subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');
subplot(2, 2, 4); imhist(W, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');

全局直方图去雾效果明显,但在图像整体上容易出现色彩失真现象。
3 局部直方图处理
clear; close all;
I = imread('images\sweden_input.jpg');
g1 = GetLocalHisteq(I(:, :, 1));
g2 = GetLocalHisteq(I(:, :, 2));
g3 = GetLocalHisteq(I(:, :, 3));In = cat(3, g1, g2, g3);figure;
subplot(2, 2, 1); imshow(I); title('原图像', 'FontWeight', 'Bold');
subplot(2, 2, 2); imshow(In); title('处理后的图像', 'FontWeight', 'Bold');
Q = rgb2gray(I);
W = rgb2gray(In);
subplot(2, 2, 3); imhist(Q, 64); title('原灰度直方图', 'FontWeight', 'Bold');
subplot(2, 2, 4); imhist(W, 64); title('处理后的灰度直方图', 'FontWeight', 'Bold');function g = GetLocalHisteq(I)
% 对灰度图像,进行局部直方图均衡化
% 输入参数:
% I——图像矩阵
% 输出参数:
% g——结果图像
% 调用库函数adapthisteq,执行局部均衡化增强
g = adapthisteq(I,'clipLimit',0.02,'Distribution','rayleigh');
end
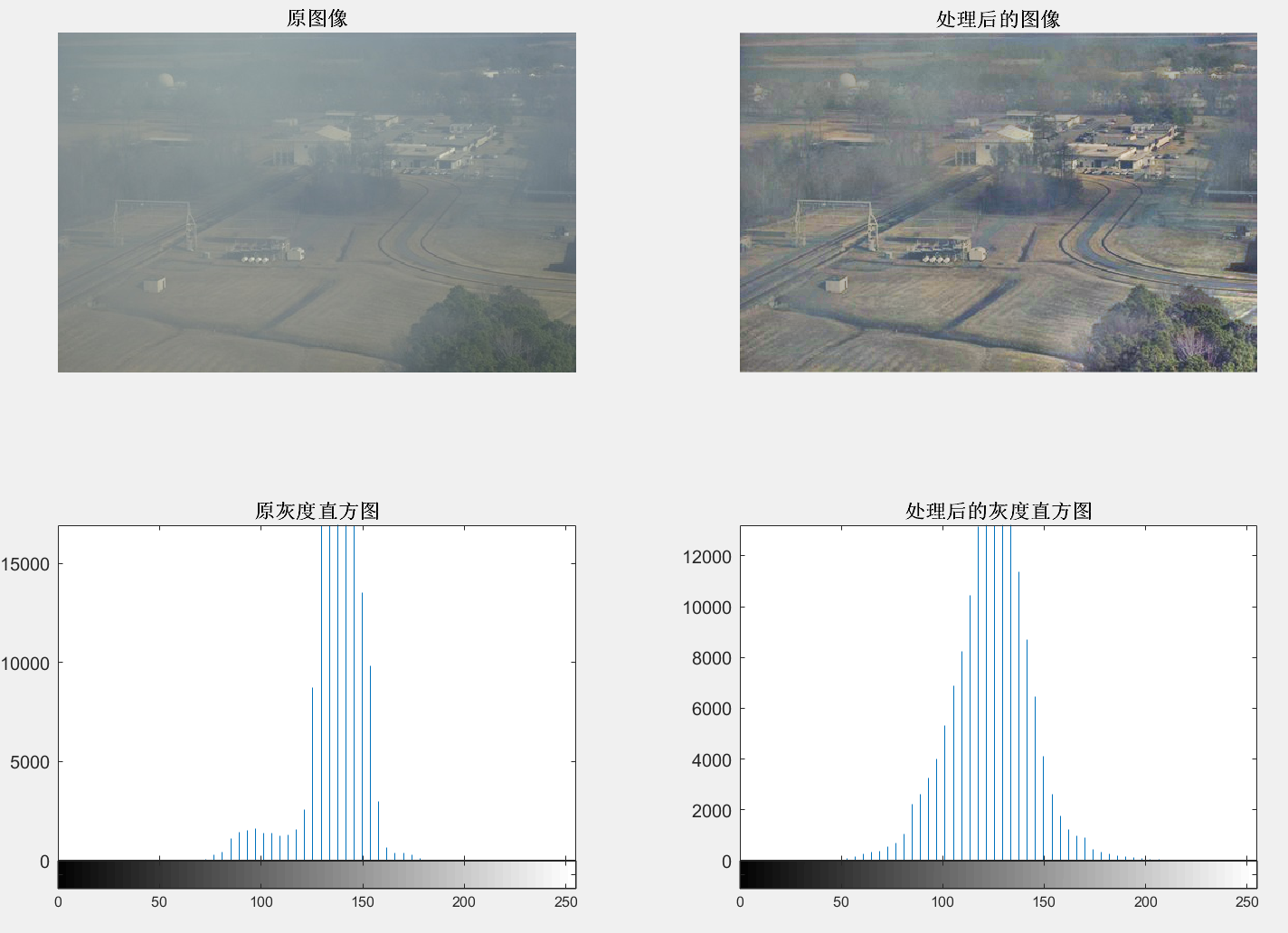
局部直方图的处理有效保持原图像的局部特征,未出现明显的色彩失真,但该图像整体的亮度偏暗,依然在某些区域模糊。
相关文章:

【MATLAB-基于直方图优化的图像去雾技术】
【MATLAB-基于直方图优化的图像去雾技术】 1 直方图均衡2 程序实现3 局部直方图处理 1 直方图均衡 直方图是图像的一种统计表达形式。对于一幅灰度图像来说,其灰度统计直方图可以反映该图像中不同灰度级出现的统计情况。一般而言,图像的视觉效果和其直方…...
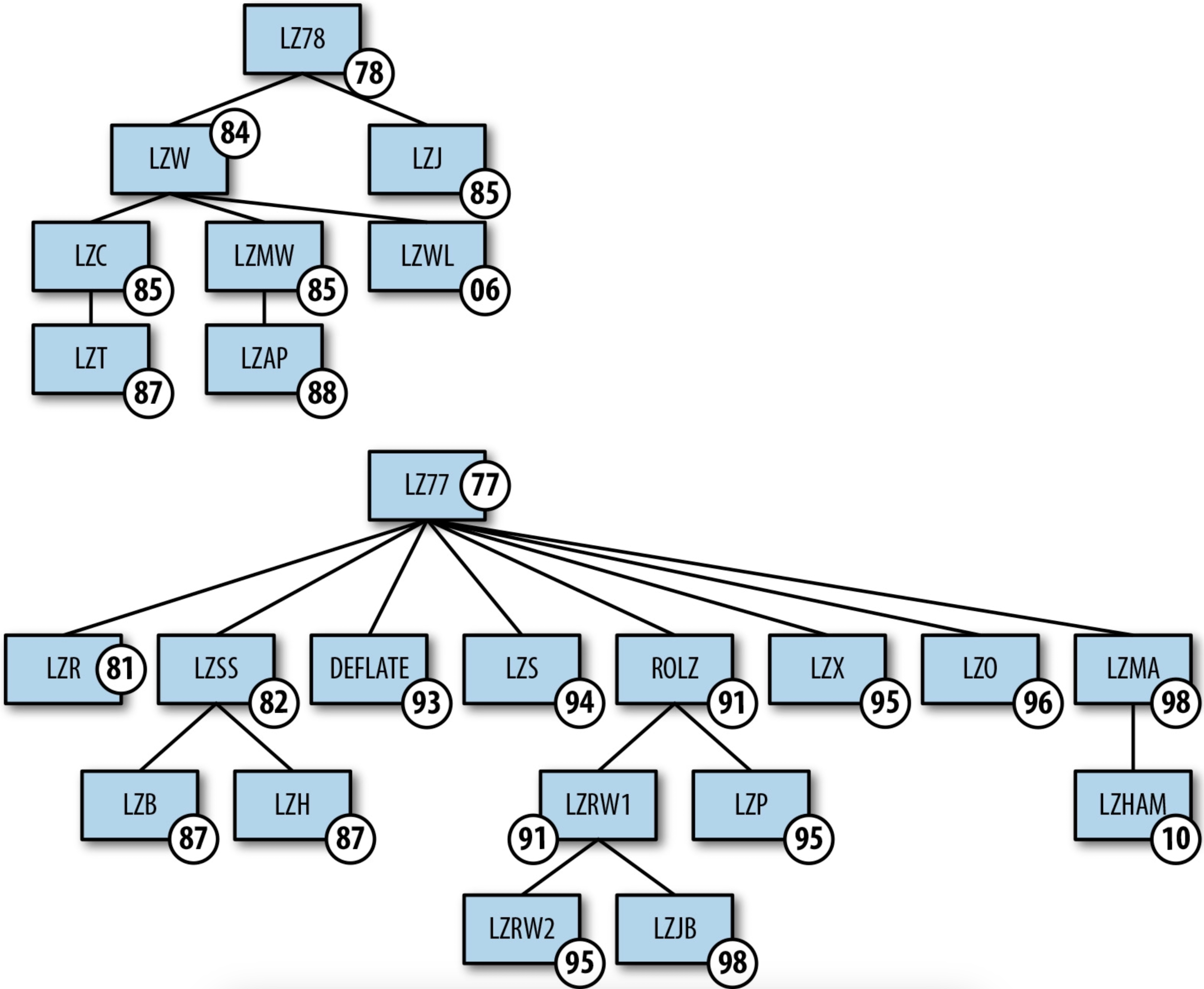
读书笔记|《数据压缩入门》—— 柯尔特·麦克安利斯 亚历克斯·海奇
前言:在接触文本隐写研究领域时了解到这本书。本书可算作《数据压缩》的入门书籍之一,这本书对熵编码、变长编码、统计编码、自适应统计编码、字典编码、上下文编码等常用编码方式的定义及来源进行介绍,对不同场景下不同格式的压缩数据有针对…...
)
Pandas进阶修炼120题-第五期(一些补充,101-120题)
目录 往期内容:第一期:Pandas基础(1-20题)第二期:Pandas数据处理(21-50题)第三期:Pandas金融数据处理(51-80题)第四期:当Pandas遇上NumPy…...
NPDP产品经理知识(产品创新管理)
复习文化,团队与领导力 产品创新管理: 如何树立愿景: 如何实现产品战略 计划 实施产品开发: 商业化,营销计划,推广活动 管理产品生命周期: 新式走向市场的流程:...
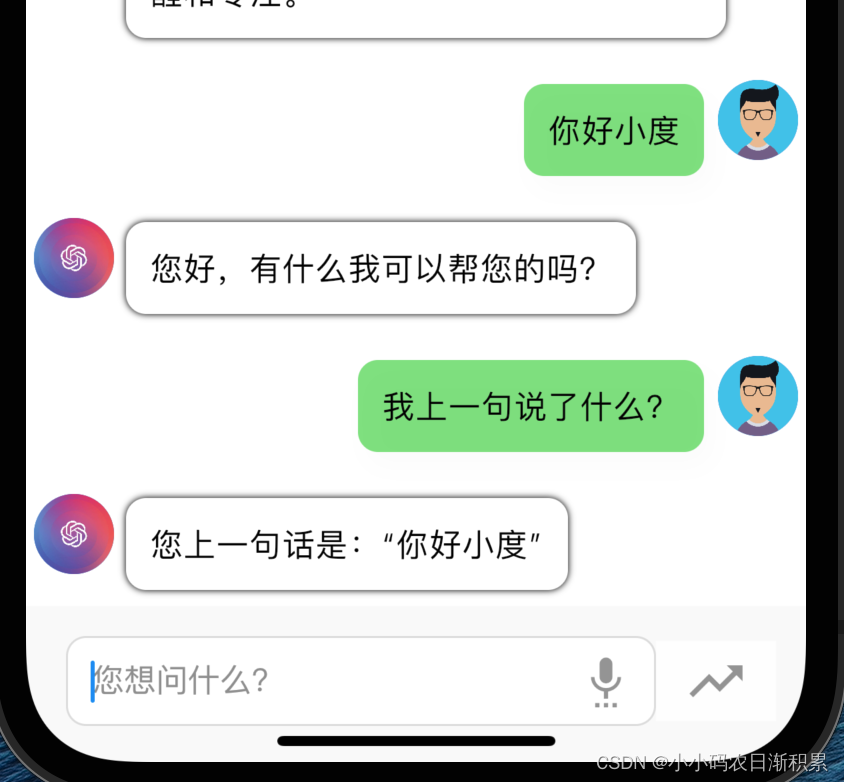
Flutter+SpringBoot实现ChatGPT流实输出
FlutterSpringBoot实现ChatGPT流式输出、上下文了连续对话 最终实现Flutter的流式输出上下文连续对话。 这里就是提供一个简单版的工具类和使用案例,此处页面仅参考。 服务端 这里直接封装提供工具类,修改自己的apiKey即可使用,支持连续…...
淘宝天猫粉丝福利购店铺优惠券去哪里找到领取网站?
淘宝天猫优惠券去哪里找到领取网站? 领取淘宝天猫粉丝福利购优惠券可通过百度搜索:草柴,进入草柴官方网站 或 手机应用商店搜索:草柴,下载安装草柴APP,就可以领取淘宝天猫优惠券; 草柴APP如何领…...

【考研复习】union有关的输出问题
文章目录 遇到的问题正确解答拓展参考文章 遇到的问题 首次遇到下面的代码时,感觉应该输出65,323。深入理解union的存储之后发现正确答案是:67,323. union {char c;int i; } u; int main(){u.c A;u.i 0x143;printf("%d,%d\n", u.c, u.i); …...
 Android 数据库Litepal)
Android学习之路(16) Android 数据库Litepal
一.LitePal的介绍 Litepal是Android郭霖大神的一个开源Android数据库的开源框架,它采用了对象关系映射(ORM)的模式,这是让我们非常好的理解的数据库,一个实体类对应我们数据库中的一个表。该库中还封装了许多的方法&a…...

Redis持久化(RDB/AOF)
"在哪里走散,你都会 找 到 我。" 认识持久化 我们在接触Mysql事务的时候,一定了解过Mysql事务的四个特性: "原子性(A)一致性(C)隔离性(I)持久性(D)" 而其中持久性其实与持久化是一回事,所谓持久与不持久&#x…...
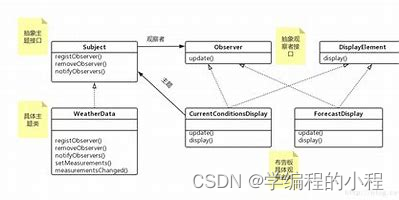
小谈设计模式(15)—观察者模式
小谈设计模式(15)—观察者模式 专栏介绍专栏地址专栏介绍 观察者模式核心思想主要角色Subject(被观察者)ConcreteSubject(具体被观察者)Observer(观察者)ConcreteObserver࿰…...
)
简单工厂模式 创建型模式(非GoF经典设计模式)
简单工厂模式是属于创建型模式,也因为工厂中的方法一般设置为静态,又叫做静态工厂方法(Static Factory Method)模式,但不属于23种GOF设计模式之一。简单工厂模式是由一个工厂对象决定创建出哪一种产品类的实例。简单工…...
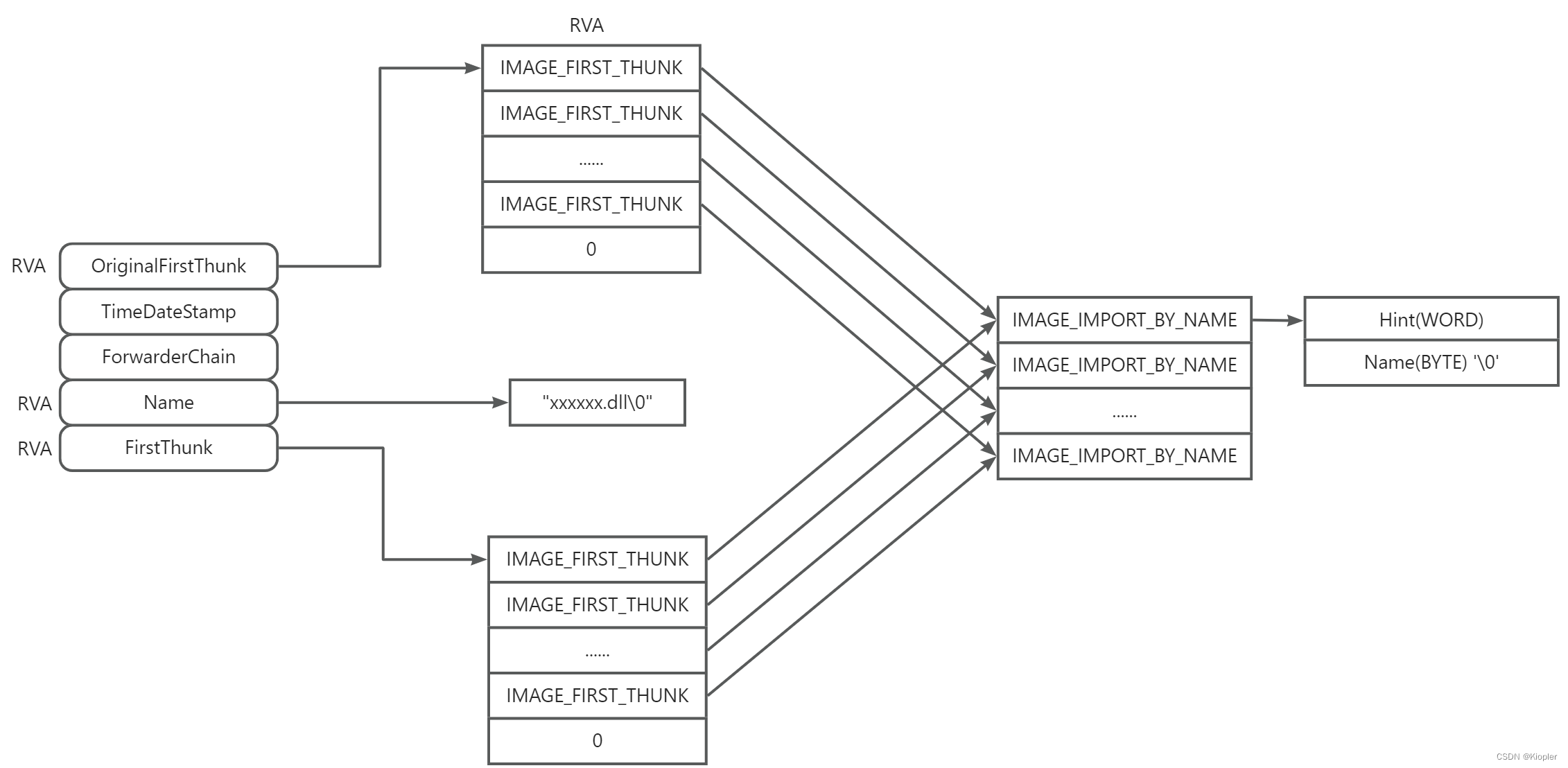
PE文件之导入表
1. 导入表 2. 显示导入表信息的例子 ; 作用: 将RVA地址转成FOA即文件偏移 ; 参数: _pFileHdr 指向读到内存中文件的基址指针 ; _dwRVA 目标RVA地址 ; 返回: 目标RVA转成文件偏移的值 RVA2FOA PROC USES esi edi edx, _pFileHdr:PTR BYTE, _dwRVA:DWORDmov esi, _pFil…...

二、码制及其转换
原码 根据我们所学可知,数字电路的逻辑电路是通过输出0和1来表示二进制数的,那么这个二进制数的正负又该怎么表示呢? 答案是在这个二进制数的最高位作为符号位来表示正负性,用0正数,用1表示负数,在这种表达…...
在pycharm中出现下载软件包失败的解决方法
一. 一般情况下我们会选择在设置中下载软件包,过程如下. 1. 直接点击左上角的文件, 再点击设置, 再点击项目, 在右边选择python解释器,点击号,输入要下载的软件包, 在下面的一系列的包中选择相对应的包,点击安装就可以了,有的时候我们下载的是最新的版本,如果要下载固定的版本…...
10.0 探索API调试事件原理
本章笔者将通过Windows平台下自带的调试API接口实现对特定进程的动态转存功能,首先简单介绍一下关于调试事件的相关信息,调试事件的建立需要依赖于DEBUG_EVENT这个特有的数据结构,该结构用于向调试器报告调试事件。当一个程序发生异常事件或者…...
文心一言 VS 讯飞星火 VS chatgpt (104)-- 算法导论10.1 2题
二、用go语言,说明如何在一个数组 A[1…n]中实现两个栈,使得当两个栈的元素个数之和不为 n 时,两者都不会发生上溢。要求 PUSH 和 POP 操作的运行时间为 O(1)。 文心一言: 在这个问题中,我们要在一个数组 A[1…n] 中…...
检测防火墙是否开启、判断程序是否加入防火墙白名单(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...
vtk 动画入门 1 代码
实现效果如图: #include <vtkAutoInit.h> //VTK_MODULE_INIT(vtkRenderingOpenGL2); //VTK_MODULE_INIT(vtkInteractionStyle); VTK_MODULE_INIT(vtkRenderingOpenGL2); VTK_MODULE_INIT(vtkInteractionStyle); //VTK_MODULE_INIT(vtkRenderingFreeType); #in…...
【VR】【unity】如何在VR中实现远程投屏功能?
【背景】 目前主流的VD应用,用于娱乐很棒,但是用于工作还是无法效率地操作键鼠。用虚拟键盘工作则显然是不现实的。为了让自己的头显能够起到小面积代替多显示屏的作用,自己动手开发投屏VR应用。 【思路】 先实现C#的投屏应用。研究如何将C#投屏应用用Unity 3D项目转写。…...

OpenGl材质
在现实世界里,每个物体会对光产生不同的反应。比如,钢制物体看起来通常会比陶土花瓶更闪闪发光,一个木头箱子也不会与一个钢制箱子反射同样程度的光。有些物体反射光的时候不会有太多的散射(Scatter),因而产生较小的高光点,而有些物体则会散射很多,产生一个有着更大半径的…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
