蓝桥杯每日一题2023.10.1
路径 - 蓝桥云课 (lanqiao.cn)

题目分析
求最短路问题,有多种解法,下面介绍两种蓝桥杯最常用到的两种解法
方法一
Floyd(求任意两点之间的最短路)注:不能有负权回路
初始化每个点到每个点的距离都为0x3f这样才能对比求出最短路
由题意先将ab差的绝对值小于等于21的边的边权赋予,还有自己到自己的边为0
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3000;
int ans = 0x3f;
int d[N][N];
int gcd(int a, int b)
{return b == 0 ? a : gcd(b, a % b);
}
int lcm(int a, int b)
{return a * b / gcd(a, b);
}
int main()
{ memset(d, 0x3f, sizeof d);for(int i = 1; i <= 2021; i ++){for(int j = 1; j <= 2021; j ++){if(abs(i - j) <= 21){d[i][j] = min(d[i][j], lcm(i, j));}}}for(int i = 1; i <= 2021; i ++)d[i][i] = 0;for(int k = 1; k <= 2021; k ++){for(int i = 1; i <= 2021; i ++){for(int j = 1; j <= 2021; j ++){d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}cout << d[1][2021];return 0;
}答案:10266837
方法二
Dijkstra(任意一点到所有点的最短路)
第一步:初始化距离 dist[1] = 0, dist[i] = +∞
第二步:找到当前没有确定点的最小值,找到最小的点之后用这个点去更新它到所有点的距离
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
int e[N], ne[N], w[N], h[N], idx, d[N];
bool st[N];
int gcd(int a, int b)
{return b == 0 ? a : gcd(b, a % b);
}
int lcm(int a, int b)
{return a * b / gcd(a, b);
}
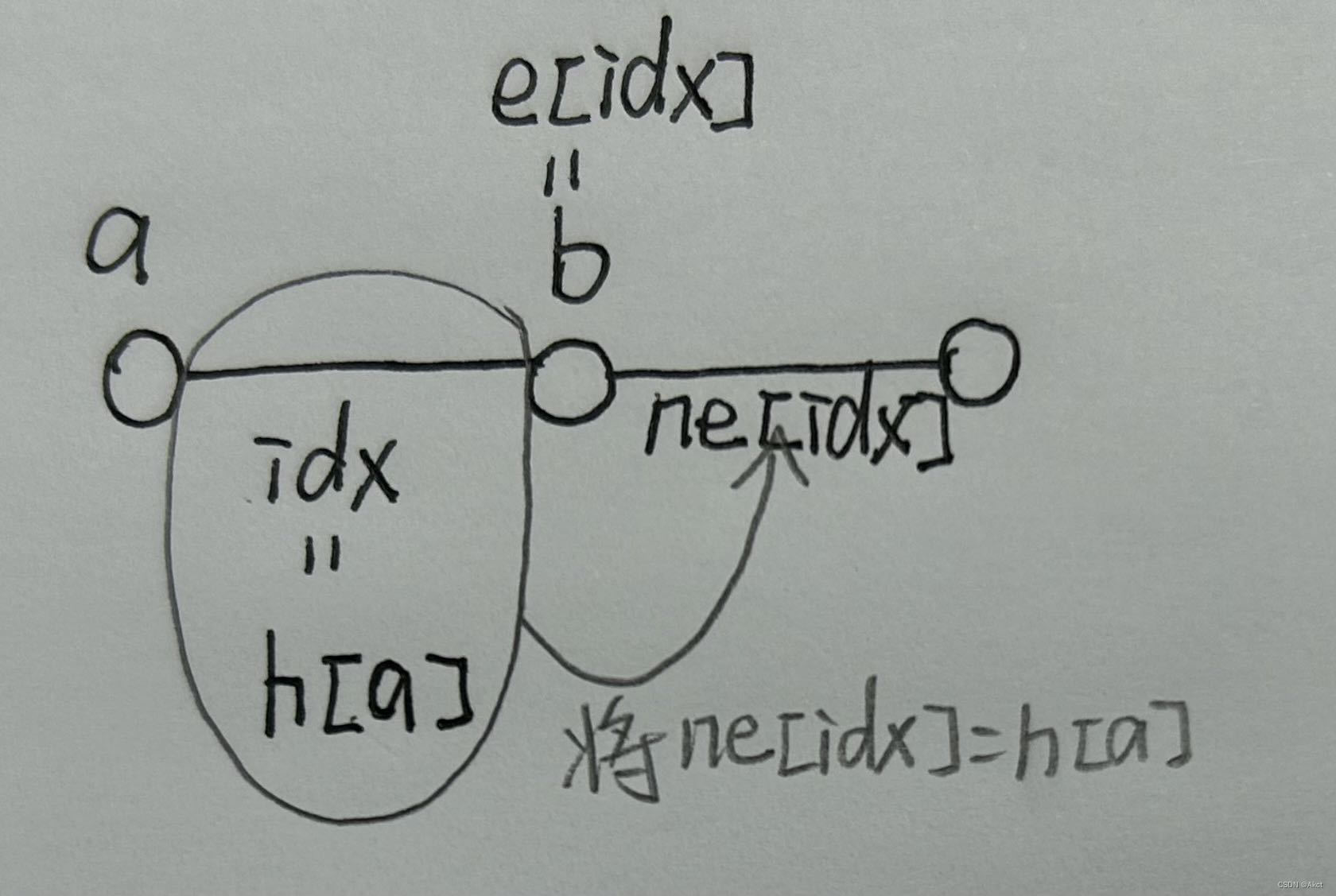
void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dijkstra()
{memset(d, 0x3f, sizeof d);d[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> q;q.push({0, 1});while(q.size()){auto t = q.top();q.pop();int num = t.second, dis = t.first;if(st[num])continue;st[num] = true;for(int i = h[num]; i != -1; i = ne[i]){int j = e[i];if(d[j] > dis + w[i]){d[j] = dis + w[i];q.push({d[j], j});}}}//if(d[2021] == 0x3f3f3f3f)return -1;return d[2021];
}
int main()
{ memset(h, -1, sizeof h);for(int i = 1; i <= 2021; i ++){for(int j = 1; j <= 2021; j ++){if(abs(i - j) <= 21){add(i, j, lcm(i, j));}}}cout << dijkstra();return 0;
}相关文章:

蓝桥杯每日一题2023.10.1
路径 - 蓝桥云课 (lanqiao.cn) 题目分析 求最短路问题,有多种解法,下面介绍两种蓝桥杯最常用到的两种解法 方法一 Floyd(求任意两点之间的最短路)注:不能有负权回路 初始化每个点到每个点的距离都为0x3f这样才能对…...
)
第三章:最新版零基础学习 PYTHON 教程(第十节 - Python 运算符—Python 中的运算符重载)
运算符重载意味着赋予超出其预定义操作含义的扩展含义。例如,运算符 + 用于添加两个整数以及连接两个字符串和合并两个列表。这是可以实现的,因为“+”运算符被 int 类和 str 类重载。您可能已经注意到,相同的内置运算符或函数对于不同类的对象显示不同的行为,这称为运算符…...
)
Nacos 实现服务平滑上下线(Ribbon 和 LB)
前言 不知道各位在使用 SpringCloud Gateway Nacos的时候有没有遇到过服务刚上线偶尔会出现一段时间的503 Service Unavailable,或者服务下线后,下线服务仍然被调用的问题。而以上问题都是由于Ribbon或者LoadBalancer的默认处理策略有关,其…...

c/c++里 对 共用体 union 的内存分配
对union 的内存分配,是按照最大的那个成员分配的。 谢谢...
博途SCL区间搜索指令(判断某个数属于某个区间)
S型速度曲线行车位置控制,停靠位置搜索功能会用到区间搜索指令,下面我们详细介绍区间搜索指令的相关应用。 S型加减速行车位置控制(支持点动和停车位置搜索)-CSDN博客S型加减速位置控制详细算法和应用场景介绍,请查看下面文章博客。本篇文章不再赘述,这里主要介绍点动动和…...
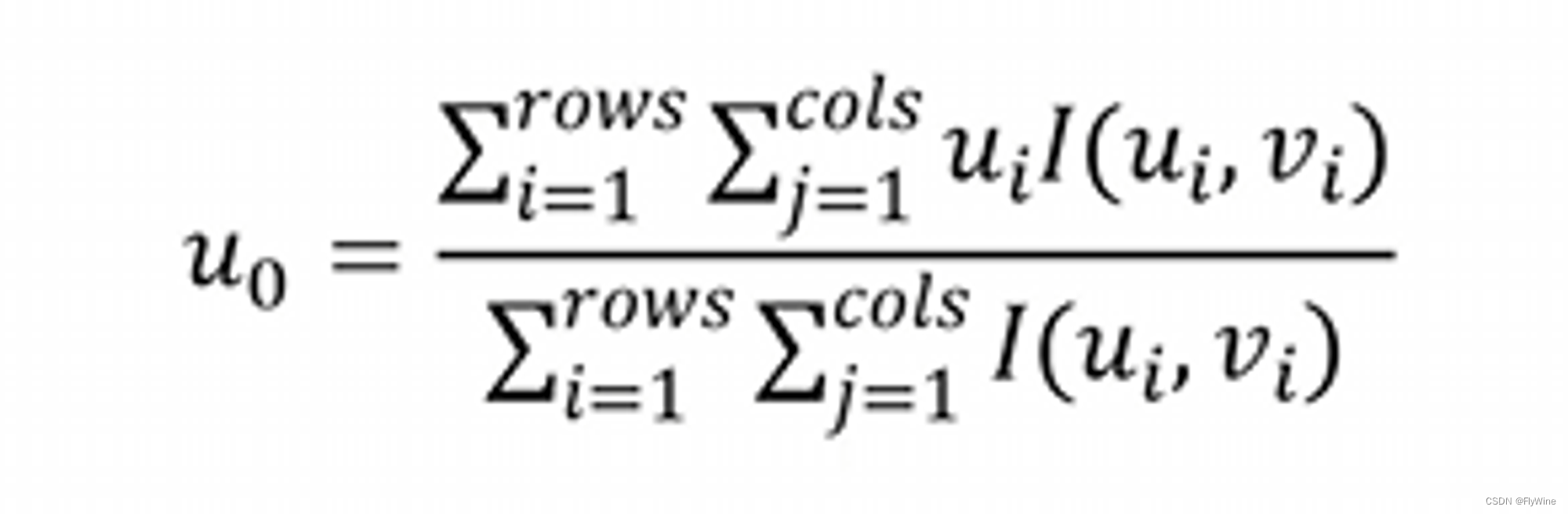
(三)激光线扫描-中心线提取
光条纹中心提取算法是决定线结构光三维重建精度以及光条纹轮廓定位准确性的重要因素。 1. 光条的高斯分布 激光线条和打手电筒一样,中间最亮,越像周围延申,光强越弱,这个规则符合高斯分布,如下图。 2. 传统光条纹中心提取算法 传统的光条纹中心提取算法有 灰度重心法、…...
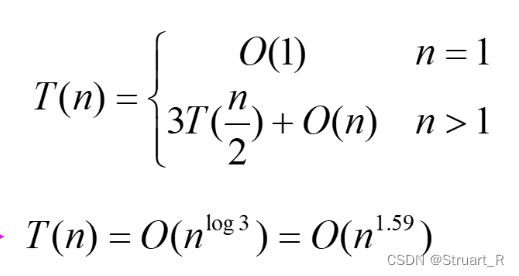
递归与分治算法(1)--经典递归、分治问题
目录 一、递归问题 1、斐波那契数列 2、汉诺塔问题 3、全排列问题 4、整数划分问题 二、递归式求解 1、代入法 2、递归树法 3、主定理法 三、 分治问题 1、二分搜索 2、大整数乘法 一、递归问题 1、斐波那契数列 斐波那契数列不用过多介绍,斐波那契提出…...
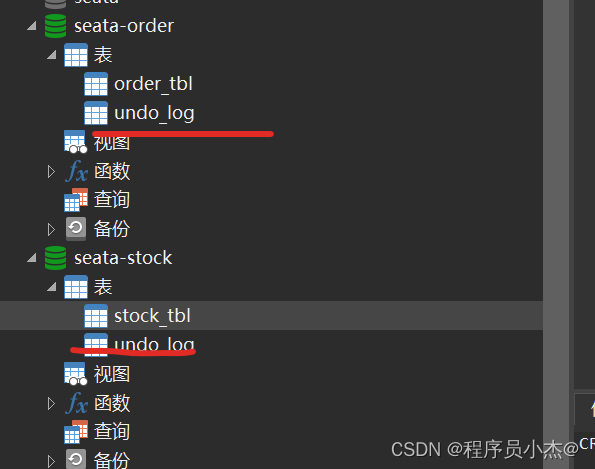
Java之SpringCloud Alibaba【六】【Alibaba微服务分布式事务组件—Seata】
一、事务简介 事务(Transaction)是访问并可能更新数据库中各种数据项的一个程序执行单元(unit)。 在关系数据库中,一个事务由一组SQL语句组成。 事务应该具有4个属性: 原子性、一致性、隔离性、持久性。这四个属性通常称为ACID特性。 原子性(atomicity) ∶个事务…...
Android逆向学习(五)app进行动态调试
Android逆向学习(五)app进行动态调试 一、写在前面 非常抱歉鸽了那么久,前一段时间一直在忙,现在终于结束了,可以继续更新android逆向系列的,这个系列我会尽力做下去,然后如果可以的话我看看能…...
音频编辑软件Steinberg SpectraLayers Pro mac中文软件介绍
Steinberg SpectraLayers Pro mac是一款专业的音频编辑软件,旨在帮助音频专业人士进行精细的音频编辑和声音处理。它提供了强大的频谱编辑功能,可以对音频文件进行深入的频谱分析和编辑。 Steinberg SpectraLayers Pro mac软件特点 1. 频谱编辑ÿ…...

基于.Net Core实现自定义皮肤WidForm窗口
前言 今天一起来实现基于.Net Core、Windows Form实现自定义窗口皮肤,并实现窗口移动功能。 素材 准备素材:边框、标题栏、关闭按钮图标。 窗体设计 1、创建Window窗体项目 2、窗体设计 拖拉4个Panel控件,分别用于:标题栏、关…...

【Rust】操作日期与时间
目录 介绍 一、计算耗时 二、时间加减法 三、时区转换 四、年月日时分秒 五、时间格式化 介绍 Rust的时间操作主要用到chrono库,接下来我将简单选一些常用的操作进行介绍,如果想了解更多细节,请查看官方文档。 官方文档:chr…...

blender快捷键
1, shift a 添加物体 2,ctrl alt q 切换四格视图 3, ~ 展示物体的各个视图按钮,(~ 就是tab键上面的键) 4,a 全选,全选后,点 ctrl 鼠标框选 减去已经选择的;…...
java Spring Boot 自动启动热部署 (别再改点东西就要重启啦)
上文 java Spring Boot 手动启动热部署 我们实现了一个手动热部署的代码 但其实很多人会觉得 这叫说明热开发呀 这么捞 写完还要手动去点一下 很不友好 其实我们开发人员肯定是希望重启这种事不需要自己手动去做 那么 当然可以 我们就让它自己去做 Build Project 这个操作 我们…...

TouchGFX之后端通信
在大多数应用中,UI需以某种方式连接到系统的其余部分,并发送和接收数据。 它可能会与硬件外设(传感器数据、模数转换和串行通信等)或其他软件模块进行交互通讯。 Model类 所有TouchGFX应用都有Model类,Model类除了存…...

cesium gltf控制
gltf格式详解 glTF格式本质上是一个JSON文件。这一文件描述了整个3D场景的内容。它包含了对场景结构进行描述的场景图。场景中的3D对象通过场景结点引用网格进行定义。材质定义了3D对象的外观,动画定义了3D对象的变换操作(比如选择、平移操作)。蒙皮定义了3D对象如何进行骨骼…...

Spring的依赖注入(DI)以及优缺点
Spring的依赖注入(DI):解释和优点 依赖注入(Dependency Injection,简称DI)是Spring框架的核心概念之一,也是现代Java应用程序开发的重要组成部分。本文将深入探讨DI是什么,以及它的…...

【强化学习】05 —— 基于无模型的强化学习(Prediction)
文章目录 简介蒙特卡洛算法时序差分方法Example1 MC和TD的对比偏差(Bias)/方差(Variance)的权衡Example2 Random WalkExample3 AB 反向传播(backup)Monte-Carlo BackupTemporal-Difference BackupDynamic Programming Backup Boot…...
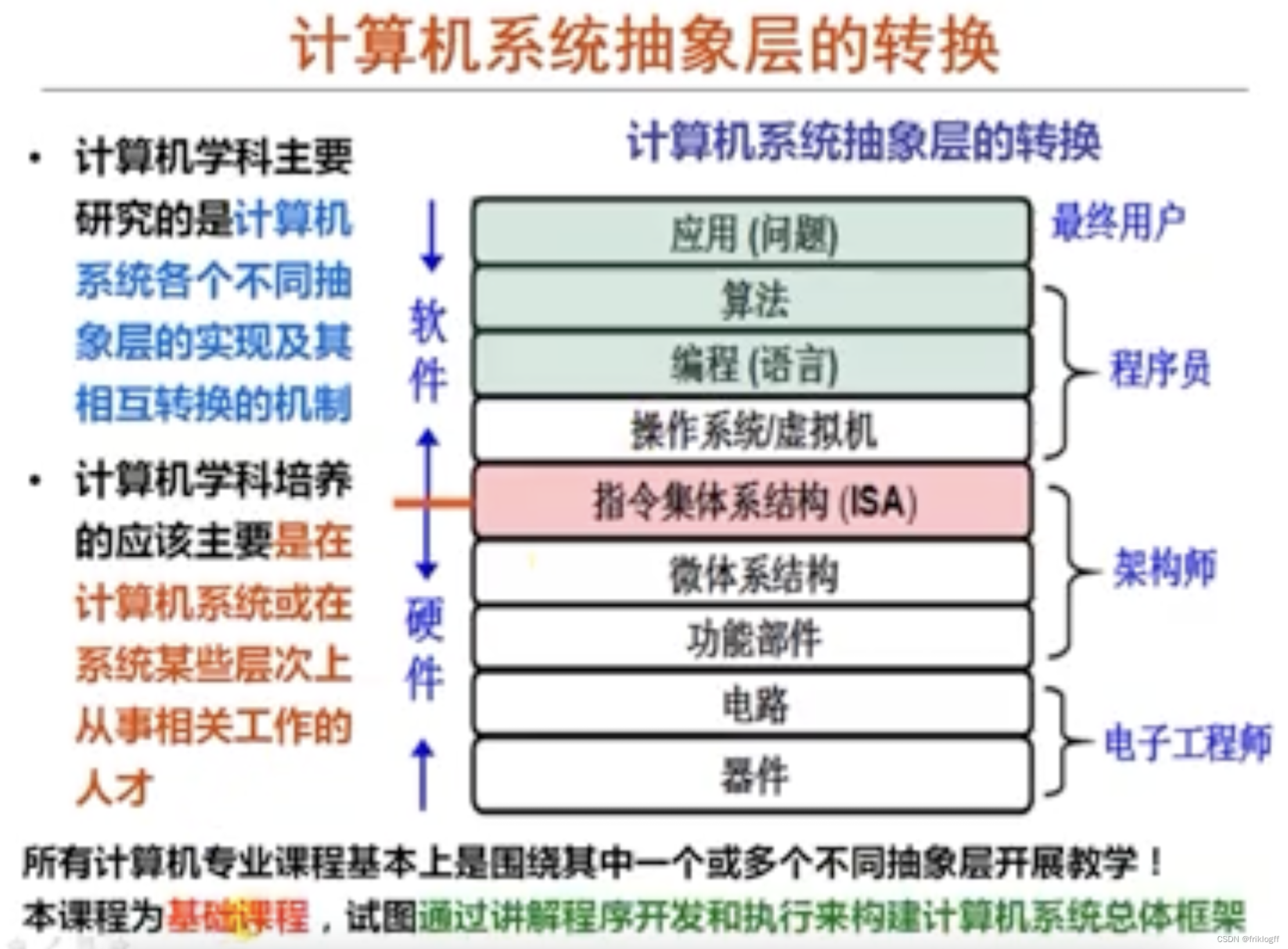
【计算机组成原理】考研真题攻克与重点知识点剖析 - 第 1 篇:计算机系统概述
前言 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术有限ÿ…...

【Java-LangChain:面向开发者的提示工程-8】聊天机器人
第八章 聊天机器人 使用一个大型语言模型的一个令人兴奋的事情是,我们可以用它来构建一个定制的聊天机器人 (Chatbot) ,只需要很少的工作量。在这一节中,我们将探索如何利用聊天的方式,与个性化(或专门针对特定任务或…...

3.1-mapper映射文件:结果映射机制
将数据库查询结果集转换为 Java 对象的核心技术 一、 核心知识点概述 MyBatis 的结果映射机制,本质是将 SQL 查询返回的数据库结果集(ResultSet),按照指定规则封装为 Java 对象(实体类、包装类等)或集合的过…...

GitHub汉化插件:让全球最大代码平台说中文
GitHub汉化插件:让全球最大代码平台说中文 【免费下载链接】github-chinese GitHub 汉化插件,GitHub 中文化界面。 (GitHub Translation To Chinese) 项目地址: https://gitcode.com/gh_mirrors/gi/github-chinese 作为全球开发者的聚集地&#x…...

YOLO26保姆级教程:从环境搭建到模型训练,小白也能轻松上手
YOLO26保姆级教程:从环境搭建到模型训练,小白也能轻松上手 1. 引言:为什么选择YOLO26? 如果你对计算机视觉感兴趣,或者工作中需要处理图片、视频里的物体识别,那你一定听说过YOLO这个名字。它就像一个视力…...

从EPS/Wind到Stata:高效转换面板数据的完整指南与常见报错解决方案
1. 为什么你的EPS/Wind数据一进Stata就“水土不服”? 做研究的朋友,尤其是经常和宏观经济、金融市场数据打交道的,肯定对EPS和Wind这两个数据库不陌生。它们就像两个巨大的数据宝库,里面装满了我们需要的各种指标。但不知道你有没…...

TFT Overlay:重构云顶之弈决策体系的智能辅助工具
TFT Overlay:重构云顶之弈决策体系的智能辅助工具 【免费下载链接】TFT-Overlay Overlay for Teamfight Tactics 项目地址: https://gitcode.com/gh_mirrors/tf/TFT-Overlay 在快节奏的云顶之弈对局中,玩家常面临三大核心痛点:装备合成…...

2.7 庐山派K230芯片I2C模块API手册:主从模式配置与Python编程实战
庐山派K230芯片I2C模块API手册:主从模式配置与Python编程实战 最近在玩庐山派K230开发板,发现它内置了5个硬件I2C模块,用起来挺方便的。I2C这个通信协议在嵌入式里太常用了,各种传感器、EEPROM存储器、触摸芯片都靠它。但很多朋友…...

C语言实战:变位词统计的高效算法与函数设计
1. 从一道OJ题说起:变位词统计的“暴力”解法与性能陷阱 很多C语言初学者,包括当年刚接触编程的我,在拿到类似NWAFU-OJ上这道“变位词统计”的题目时,第一反应往往是“这不难”。题目要求很明确:给你一个文本字符串和一…...

Scan2CAD:三维扫描到CAD模型的效率革命——AI驱动的建筑数字化技术突破
Scan2CAD:三维扫描到CAD模型的效率革命——AI驱动的建筑数字化技术突破 【免费下载链接】Scan2CAD [CVPR19] Dataset and code used in the research project Scan2CAD: Learning CAD Model Alignment in RGB-D Scans 项目地址: https://gitcode.com/gh_mirrors/s…...

COMSOL裂缝地层的THM耦合,离散裂缝模型,随机复杂裂缝,适合地热能研究。 增强地热系统...
COMSOL裂缝地层的THM耦合,离散裂缝模型,随机复杂裂缝,适合地热能研究。 增强地热系统,热流固耦合的开采过程。地下几千米藏着巨大的热能宝藏,增强型地热系统(EGS)就像给地球做"心脏搭桥手术…...

一次线上事故排查:200 行 ERROR 日志定位根因
如果你做过运维或者后端开发,一定遇到过这种情况。 线上报警: ERROR 日志激增第一反应通常是: 系统是不是挂了?于是开始排查日志。 一、事故背景 某天生产环境出现报警: 服务:oa-server 报警ÿ…...
