XrayGLM - 医学大模型
文章目录
- 关于 XrayGLM
- 研究背景
- VisualGLM-6B
关于 XrayGLM
XrayGLM: 首个会看胸部X光片的中文多模态医学大模型 | The first Chinese Medical Multimodal Model that Chest Radiographs Summarization.
基于VisualGLM-6B 微调
- github : https://github.com/WangRongsheng/XrayGLM
研究背景
MiniGPT-4 [1] 在500万全英文数据集(LAION+CC3M+CC12M+SBU)上预训练,并在3200多张高质量图像数 据描述上进行微调。
希望有一个原生支持中文预训练的多 模态模型来支持我们的一些工作
通用领域的多模态大模型风声水起,如MiniGPT-4,然而,此类多模态大模型却很少出现在医学领域的研 究中,阻碍了相关研究发展。
MedCLIP 提出了 X-ray 和配对报告的公开数据集。XrayGPT 基于 MiniGPT-4 的思路训练了一个X-ray的医学多模态模型。
OpenI 一份是来自印第安纳大学医院的胸部 X 光图 像数据集,包含 6,459 张图像和 3,955 份报告。
VisualGLM-6B
VisualGLM-6B [1] 是一个开源的,支持图像、中文和英文的多模态对话语言模型,语言模型基 于 ChatGLM-6B,具有 62 亿参数;
图像部分通 过训练 BLIP2-Qformer 构建起视觉模型与语言 模型的桥梁,整体模型共78亿参数。
VisualGLM-6B 依靠来自于 CogView 数据集的 30M高质量中文图文对,与300M经过筛选的 英文图文对进行预训练,中英文权重相同。该 训练方式较好地将视觉信息对齐到ChatGLM的 语义空间;之后的微调阶段,模型在长视觉问 答数据上训练,以生成符合人类偏好的答案。
XrayGLM基于VisualGLM-6B进行微调训练而来。借助ChatGPT构建了一个可用于支持中文训练的X-ray影像- 诊疗报告对。
XrayGLM微调实践
1、克隆XrayGLM repo:
git clone https://github.com/WangRongsheng/XrayGLM.git
2、 安装依赖:
pip install -r requirements.txt
# 国内换源安装依赖
pip install -i https://mirrors.aliyun.com/pypi/simple/ -r requirements.txt
3、准备数据集:
./data/Xray/
├── 1000_1.png
├── 1000_2.png
├── ...
└── openi-zh.json
4、配置训练文件finetune_XrayGLM.sh
5、开启微调训练:
# 报错:CUDA out of memory. Tried to allocate 20.00 MiB (GPU 4; 3.82 GiB total capacity; 2.94 GiB already allocated; 6.62 MiB free; 3.06 GiB reserved in total by PyTorch) If reserved memory is >> allocated memory try setting max_split_size_mb to avoid fragmentation. See documentation for Memory Management and PYTORCH_CUDA_ALLOC_CONF# 设置CUDA变量,解决直接训练而出现无法正确加载到显卡问题 export CUDA_VISIBLE_DEVICES=0,1,2,3# 开始训练
bash finetune_XrayGLM.sh# 训练过程很快,四卡A100训练2-3个小时就可以完成!
6、CLI测试:
python cli_demo.py \
--from_pretrained checkpoints/$fintune_weights$ \ --prompt_zh '详细描述这张胸部X光片的诊断结果'- max_length: 总序列的最大长度
- top_p
- top_k
- temperature:采样温度
- …
7、WebUI测试:
python web_demo.py \
--from_pretrained checkpoints/$fintune_weights$1、不同的prompt构建对于整个模型的回答是否有影响?
{"img": "fewshot-data/pig.png", "prompt": "这张图片的背景里有什么内容?", "label": "这张图片的背景是是虚化的。"},
{"img": "fewshot-data/meme.png", "prompt": "这张图片的背景里有什么内容?", "label": "这张图片的背景是蓝色的木质地板。"},{"img": "./data/Xray/162_1.png", "prompt": "通过这张胸部光照片,可以诊断出什么?", "label": "根据X射线图像,心脏大小正常,胃部看起来很清晰。已经排除了胃炎、积液、水肿、气胸、腰病、结节或胃块的存在。该发现表明一切正常。2、大模型训练中,训练的精度(int4,int8,float16…)不是特别重要,模型的参数(6B、13B…) 很影响模型的性能。
3、如果数据多的话可以考虑增加训练的参数,目前的训练脚本只训练了2层lora:
https://github.com/THUDM/VisualGLM-6B/issues/61#issuecomment-1562856845
未来展望
- 模型的能力更多来源于数据的支持,OpenI-zh作为微调数据集,其数据量足以支持研究,在更广泛的 任务和性能表现上,我们认为在大规模数据集上预训练并在高质量少量数据集上微调是一种可行的方案;
- 普遍意义的理解上,视觉多模态模型=视觉模型+语言模型。除了需要关注视觉模型信息与语言模型输 出的搭配外,还需要额外关注到语言模型的加强,在人机的对话中,尤其是医疗语言模型的问答上,除 了专业的医疗问题回答,带有人文情怀的有温度的回答更应该是我们追寻的目标;
2023-10-03
相关文章:

XrayGLM - 医学大模型
文章目录 关于 XrayGLM研究背景VisualGLM-6B 关于 XrayGLM XrayGLM: 首个会看胸部X光片的中文多模态医学大模型 | The first Chinese Medical Multimodal Model that Chest Radiographs Summarization. 基于VisualGLM-6B 微调 github : https://github.com/WangRongsheng/Xra…...
)
Hive 常见数据倾斜场景及解决方案(Map\Join\Reduce端)
目录 MapReduce流程简述a) Map倾斜b) Join倾斜c) Reduce倾斜 首先回顾一下MapReduce的流程 MapReduce流程简述 输入分片: MapReduce 作业开始时,输入数据被分割成多个分片,每个分片大小一般在 16MB 到 128MB 之间。这些分片会被分配给不同的…...

C++中的四种强制类型转换符详解
前 言 C 既支持 C 风格的类型转换,又有自己风格的类型转换。C 风格的转换格式很简单,但是有不少缺点: 转换太过随意,可以在任意类型之间转换。你可以把一个指向 const 对象的指针转换成指向非 const 对象的指针,把一…...

Windows电脑多开器的优缺点对比
Windows电脑多开器是一种能够让用户同时运行多个应用程序、游戏或者网页的软件工具。它的作用在于让用户能够更加高效地工作、学习或者娱乐。但是,这种软件也存在一些优劣势的对比。 优点: 提升工作效率。多开器可以让用户同时打开多个应用程序或者网页…...
Java笔记六(面向对象:类与对象)
面向对象编程的本质:以类的方式组织代码,以对象的组织(封装)数据 抽象 三大特征:封装 继承 多态 从认识角度考虑是先有对象后有类。对象,是具体的事物。类,是抽象的,是对对象的抽…...
Git使用【中】
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析3 目录 👉🏻分支管理分支概念git branch(查看/删除分…...

Greenplum7一键安装
2023年9月底,Greenplum 发布了7.0.0版本,并于2023年10月03日开放了安装部署说明文档,现在快速尝鲜版的docker一键部署方式如下: mkdir /data/gpdb docker run -d --name greenplum -p 15432:5432 -v /data/gpdb:/data inrgihc/g…...
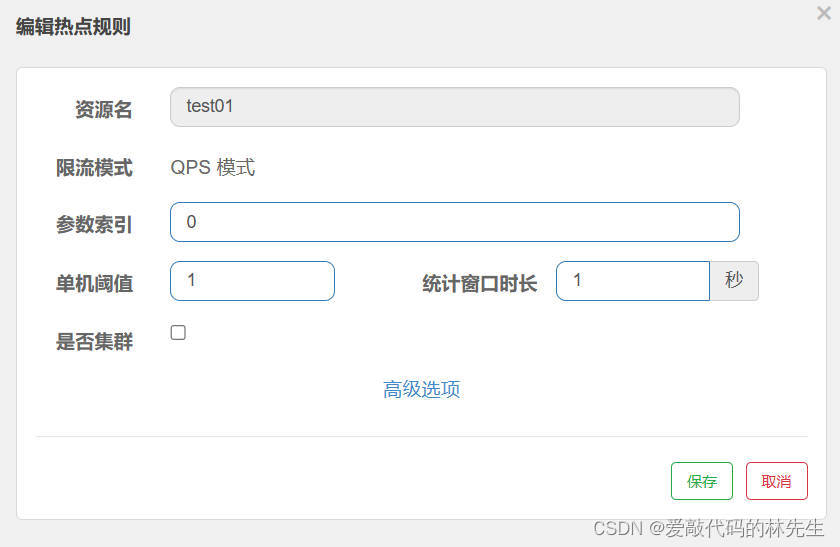
Springboo整合Sentinel
Springboo整合Sentinel 1.启动Sentinel java -jar sentinel-dashboard-1.8.6.jar2.访问localhost:8080到Sentinel管理界面(默认账号和密码都是sentinel) 3.引入依赖(注意版本对应) <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spr…...
python爬取csdn个人首页中的所有封面
#爬取csdn个人首页中的所有封面 import requests import json import reurlhttps://blog.csdn.net/community/home-api/v1/get-business-list? headers{User-Agent:Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/117.0.0.0 Safar…...

EasyHttp - 网络请求,如斯优雅
官网 项目地址:Github博客地址:网络请求,如斯优雅 OkHttp 另外对 OkHttp 原理感兴趣的同学推荐你看以下源码分析文章 OkHttp 精讲:拦截器执行原理OkHttp 精讲:RetryAndFollowUpInterceptorOkHttp 精讲:…...

【Java】Stream的基本使用
Stream特点 Stream的一系列操作组成了Stream的流水线, Stream流水线包含: 数据源: 这里的数据源可能是集合/数组, 可能是生成器, 甚至可能是IO通道(Files.lines)零个或多个中间操作: 中间操作会导致流之间的转化, 如filter(Predicate)一个终端操作: 终端操作会产生最终所需要的…...
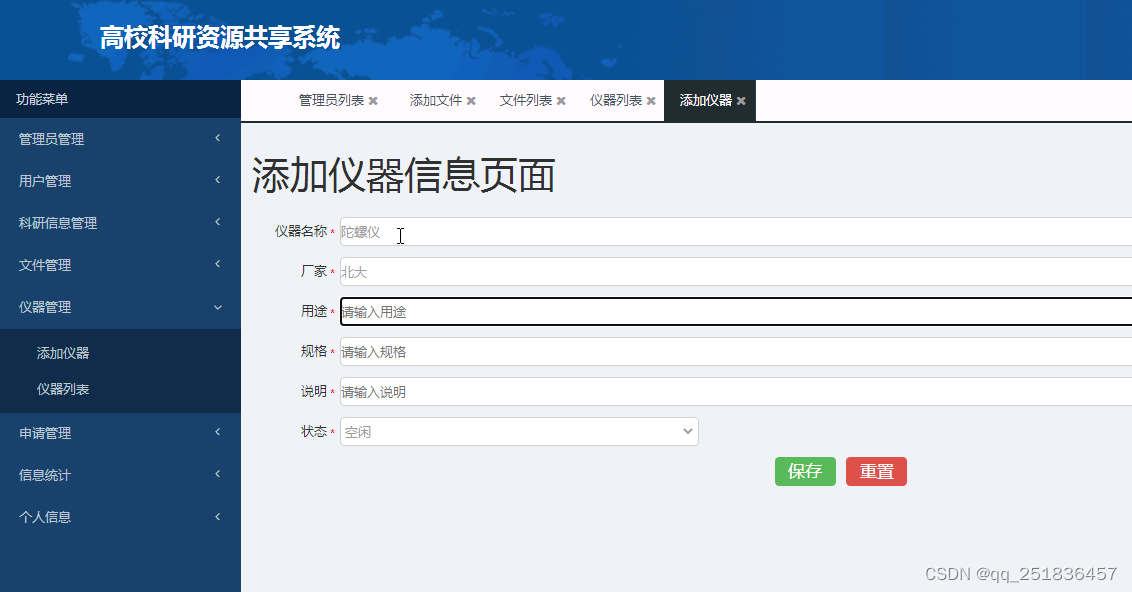
idea Springboot 高校科研资源共享系统VS开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 springboot 高校科研资源共享系统是一套完善的信息系统,结合springboot框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用springboot框架(MVC模式开发), 系统具有完整的源代码和数据…...
机器学习算法基础--K-means应用实战--图像分割
目录 1.项目内容介绍 2.项目关键代码 3.项目效果展示 1.项目内容介绍 本项目是将一张图片进行k-means分类,根据色彩k进行分类,最后比较和原图的效果。 题目还是比较简单的,我们只要通过k-means聚类,一类就是一种色彩得出聚类之…...
CSS学习小结
css的两种使用方式: ①内嵌样式表 ②导入外部样式表(实际开发常用)<link href"...." rel"stylesheet"/> 选择器: ①标签选择器:通过标签种类决定 ②类选择器:class"..…...

数据挖掘实验(一)数据规范化【最小-最大规范化、零-均值规范化、小数定标规范化】
一、数据规范化的原理 数据规范化处理是数据挖掘的一项基础工作。不同的属性变量往往具有不同的取值范围,数值间的差别可能很大,不进行处理可能会影响到数据分析的结果。为了消除指标之间由于取值范围带来的差异,需要进行标准化处理。将数据…...
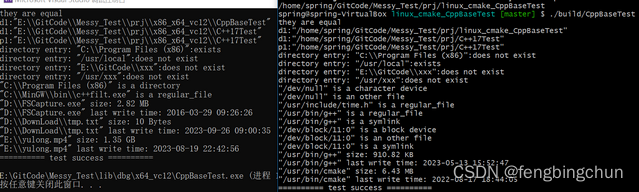
C++17中std::filesystem::directory_entry的使用
C17引入了std::filesystem库(文件系统库, filesystem library)。这里整理下std::filesystem::directory_entry的使用。 std::filesystem::directory_entry,目录项,获取文件属性。此directory_entry类主要用法包括: (1).构造函数、…...
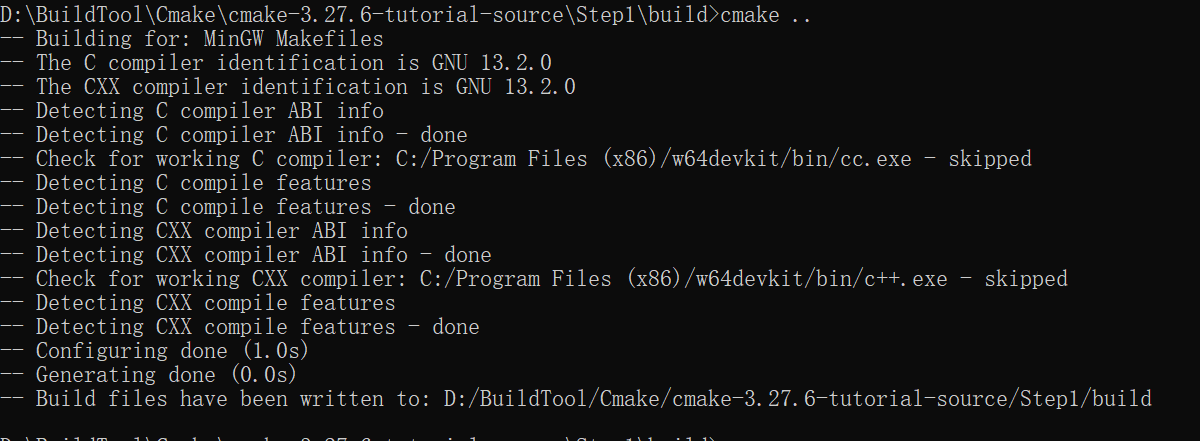
C/C++跨平台构建工具CMake入门
文章目录 1.概述2.环境准备2.1 安装编译工具2.2 安装CMake 3.编译一个示例程序总结 1.概述 本人一直对OpenGL的3d渲染很感兴趣,但是苦于自己一直是Android开发,没有机会接触这方面的知识。就在最近吗,机会来了,以前一个做3D渲染的…...
【CFD小工坊】浅水方程的离散及求解方法
【CFD小工坊】浅水方程的离散及求解方法 前言基于有限体积法的方程离散界面通量与源项计算干-湿网格的处理数值离散的稳定性条件参考文献 前言 我们模型的控制方程,即浅水方程组的表达式如下: ∂ U ∂ t ∂ E ( U ) ∂ x ∂ G ( U ) ∂ y S ( U ) U…...

第十四章 类和对象——C++对象模型和this指针
一、成员变量和成员函数分开存储 在C中,类内的成员变量和成员函数分开存储 只有非静态成员变量才属于类的对象上 class Person {public:Person() {mA 0;}//非静态成员变量占对象空间int mA;//静态成员变量不占对象空间static int mB; //函数也不占对象空间&#…...

计算机竞赛 深度学习卫星遥感图像检测与识别 -opencv python 目标检测
文章目录 0 前言1 课题背景2 实现效果3 Yolov5算法4 数据处理和训练5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **深度学习卫星遥感图像检测与识别 ** 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
